Open Journal of Applied Sciences, 2013, 3, 58-64
Published Online March 2013 (http://www.scirp.org/journal/ojapps)
Performance Evaluation of Various Functions for Kernel
Density Estimation
Youngsung Soh, Yongsuk Hae, Aamer Mehmood, Raja Hadi Ashraf, and Intaek Kim
Department of Information and Communication Engineering, Myongji University, Yongin, 449-728, Korea
Received 2012
ABSTRACT
There have been vast amount of studies on background modeling to detect moving objects. Two recent reviews[1,2]
showed that kernel density estimation(KDE) method and Gaussian mixture model(GMM) perform about equally best
among possible background models. For KDE, the selection of kernel functions and their bandwidths greatly influence
the performance. There were few attempts to compare the adequacy of functions for KDE. In this paper, we evaluate the
performance of various functions for KDE. Functions tested include almost everyone cited in the literature and a new
function, Laplacian of Gaussian(LoG) is also introduced for comparison. All tests were done on real videos with vary-
ing background dynamics and results were analyzed both qualitatively and quantitatively. Effect of different bandwidths
was also investigated.
Keywords: Background Model; Kernel Density Estimation; Kernel Functions
1. Introduction
The detection of moving objects is one of the challenging
problems in video surveillance system due to changes of
natural phenomena occurred in a scene. Background sub-
traction is commonly used for detecting moving objects
especially when background has not much change. The
most important issue in background subtraction is main-
taining background. Many background modeling tech-
niques were proposed by researchers. Among them are
running Gaussian average[3], GMM[4], KDE[5], and
eigenb a ckground [ 6 ] . Excellent reviews of these tech-
niques are presented in [1,2]. In [1,2], GMM and KDE
were shown similar performance and outstrip others.
For KDE, the selection of kernel functions and their
bandwidths is important in that they determine the un-
derlying probability distribution and thus the quality of
background modeling. While surveying the literature, we
found one relevant work on kernel function comparisons.
Zucchini[7] compared five kernel functions for KDE. He
argued that Epanechnikov function performed best. The
performance measure used was mean integrated squared
error(MISE). He derived the results only in theoretical
manner and never tested on real video.
In this paper, we tested nine kernel functions where eight
of them are frequently cited in the literature. One new
function, LoG, is introduced for comparison. All tests
were done on real videos with varying background dy-
namics and results were analyzed both qualitatively and
quantitatively. Effect of different bandwidths was also
investigated. For quantitative comparison, we used recall
and precision as performance measures and ROC curves
were drawn to show the results.
The paper is structured as follows. In section 2, we
describe the related work. Proposed method is introduced
in section 3. Experimental results and a na l ys i s are ex-
plained in section 4. Finally section 5 gives conclusion
and future work.
2. Related Works
Zucchini [7] compared the performance of five kernel
functions for KDE. They are Epanechnikov, Gaussian,
uniform, triangular, and bi weight functions. He used
MISE as a performance measure. We follow the nota-
tions used in [7] to explain his approach below. Mean
squared error(MSE) of estimated function is given as
Equations (1), (2), and (3).
))()((
^
^
2
))((
xfx
f
f
ExMSE
−
=
(1)
))()(())()((
^^
^
22
())((
xEfx
f
xfx
f
f
EExMSE
−−
+=
(2)
)()())(( )()(
^^
2
^
xfxf
Bias
f VarxMSE +=
(3)
Here
)(xf
and
)(
ˆxf
represent original probability den-
sity function and estimated probability density function
respectively. Bias and variance are two components of
MSE. The theoretical derivation of bias and variance can

Y. SOH ET AL.
be found in [7] and given as,
)(
2
))(( //
2
2 ^
xxBias f
k
h
f≈ (4)
dzzxf
nh
xVar
K
f
)()(
1
))((
2
^∫
≈
(5)
, where n and h represent the number of previous samples
and bandwidth respectively. Substituting Equations (4)
and (5) for Equation (3), we get
jxf
kh
f
nh
xMSE
2
2//
2
2
4
^
1
(
4
1
))((
)
+=
(6)
, where
dzzK
z k
)(
2
2
∫
≈
and
∫
≈dzk
zj)
2
2(
. Global accu-
racy of
)(
^
xf
is MISE defined as in Equations (7) and
(8).
∫∫
∞
∞−
∞
∞−
+= dxVardxxMISE xfxf
Bias
f)()())(( )()(
^^
2
^
(7)
jxf
kh
fnh
dxxMISE 2
2//
2
2
4
^1
(
4
1
))(( )+= ∫ (8)
MISE measure is used to quantify the performance of the
estimator. Optimal bandwidth can be calculated by mi-
nimizing the Equation (8) with respect to h and is given
as
)
)(
(
4
2
2
2
4
5
1
4
5
)(
^
n
k
j
f
f
MISE
OPT
β
=
(9)
, where
∫
=.)(
)(
2//
dxf
xf
β
Wand and Jones[8] used
MISE given in Equation (9) to measure the performance
of various kernel functions and found that Epanech-
nikov kernel is the best.
Assuming the effic i e ncy of Epanechnikov function is
100% , the efficiency of other kernels were calculated
and given as in Table 1. As can be seen, not much dif-
ference is observed among various kernel functions
though Epanechnikov function achieves the best.
Table 1. Kernel functions and their efficiencies
Kernel Efficiency
Epanechnikov 100%
Bi weight 99.39%
Triangular 98.59%
Gaussian 95.12%
Rectangular 92.95%
3. The Proposed Method
We follow the notations used in [5] to explain the pro-
posed method. Let
xxx N
,...
2,1
be previous N sampl es of
intensity values for some pixel. Given these sampl es,
KDE is used to estimate probability density at any inten-
sity value of the pixel. Let
xt
be an intensity value of
the pixel at time t. Then we can estimate probability den-
sity for pixel value
xt
as in Equation (10).
1
()( )
1
N
x xx PK
rt ti
i
N
σ
= −
∑=
(10)
where K is a kernel function and
σ
is bandwidth. For
more than one dimension, Equation (11) is used.
(11)
, where
K σ
is a kernel function for d dimensional space.
In our work, we assume d = 1. The pixel is considered to
be foreground if the above probability estimate is less
than some threshold value.
3.1. Kernel Functions
Kernel function K (t) described in Equation (11) should
satisfy three conditions . They are :
1) K (t) >= 0,
2) K (t) should be symmetric, and
3)
∫=1)( dttK
.
We collected almost all the kernel functions cited in
the literature that were used for KDE. There were eight
candidate functions: uniform, triangular, quartic, tri
weight, tri cube, cosine, Epanechnikov, and Gaussian
functions. We add one more function, LoG, for com-
parison. Their names, formula with value range, and
graphs are given in Table 2. For LoG, since negative
value violates condition 1) above, we use the range
where the function value is nonnegative.
3.2. Selection of Threshold
Elgammal, Duraiswami, Harwood, and Davis[5] seemed to
select threshold value empirically for Gaussian kernel to
differentiate between background and foreground. Thre-
shold selection guideline for all other kernels we consi-
dered in this paper is rarely found in the literature. Inten-
sive empirical study led us to the conclusion that around
85% of the maximum probability density value that each
kernel function can provide gave the best results. To re-
duce the computation time that is the major drawback of
KDE, we built lookup table having pre-calculated func-
tion values for all possible domain values for each ker-
nel.
3.3. Selection of Bandwidth
Elgammal, Duraiswami, Harwood, and Davis [5] showed
59

Y. SOH ET AL.
how to select optimal bandwidth for Gaussian kernel.
However, bandwidth selection guideline for all other
Table 2. Kernel functions, formula, and their graphs
Kernel E qua tion
K(u)= Diagram
Uniform









≤
Otherwise
uif
0
112/1
Trian gu-
lar









≤=−
Otherwise
uif
0
111
µ
Qua rtic









≤=
−
Otherwise
uif
u
0
11
)
2
1( 2
16
15
Tri
weigh t









≤=
−
Otherwise
uif
u
0
11
)
2
1( 3
32
35
Tri cube









≤=
−
Otherwise
uif
u
0
11
)
3
1(
3
81
70
Cosin e









≤=
Otherwise
uif u
0
11 )
2
cos(
4
ππ
Epa-
nec hn i-
kov









≤=
−
Otherwise
uif
u
0
11
)
2
1(
4
3
Lapla-
cian of
Gaussian









≤=
−
−
Otherwise
uif
e
u
u
0
11 2
2
)
2
2
1(
1
π
kernels we considered is rarely found in the literature.
Thus we empirically chose several bandwidth values and
analyze the behavior of each kernel function.
4. Experimental Results
In this section, we compare the performance of various
kernel functions for KDE both qualitatively and quantita-
tively. We use three test video sets that were used for the
competition of background and foreground separation in
VSSN2006 Conference[9]. Following are abbreviations
for each data set.
STATIC : Background is almost static.(749 frames)
MILD : Background has mild dynamic behavior.(749
frames)
SEVERE : Background has severe dynamic beha-
vior .( 819 frames)
For all three, background is real and foreground is ar-
tificial, i.e., graphically generated objects are inserted
and animated in real background video. The reason for
doing this is in the easiness of getting ground truth. The
size of the image is 320x240 for all test videos.
4.1. Qualitative Analysis
Figure. 1 shows the result for STATIC. Figure. 1(a) is
(a) (b)
(c)
(d) (e)
(f)
(g) (h)
(i)
(j) (k)
Figure 1. (a) Original frame, (b) Ground Truth, (c) Tri-
angular, (d)Gaussian, (e) Epanechnikov, (f) Quartic, (g) Tri
weight , (h) Tri cube, (i) Cosine, (j) Uniform, and (k) Lapla-
cian of Gaussian
60

Y. SOH ET AL.
(a) (b)
(c)
(d) (e)
(f)
(g) (h)
(i)
(j) (k)
(i)
Figure 2. (a) Original frame, (b) Ground Truth, (c) Tri-
angular, (d)Gaussian, (e) Epanechnikov, (f) Quartic, (g) Tri
weight , (h) Tri cube, (i) Cosine, (j) Uniform, and (k) Lapla-
cian of Gaussian
the original frame, 1(b) the ground truth, and 1(c)
through 1(k) the foreground detection results for nine
kernel functions respectively. Bandwidths used for all
kernel functions were set to 20. Since the video contains
almost no dynamic background activities, all functions
performed about equally well, though uniform kernel
found somewhat less true positives.
Figure. 2 and Figure. 3 depict the results for MILD
and SEVERE videos respectively. Conventions for each
image in Figure. 2 and Figure. 3 are the same as the one
for Figure. 1. LoG seems to be the worst in terms of de
tecting false positives and uniform kernel performed
(a) (b)
(c)
(d) (e)
(f)
(g) (h)
(i)
(j) (k)
Figure 3. (a) Original frame, (b) Ground Truth, (c) Trian-
gula r , (d)Gaussian, (e) Epanechnikov, (f) Quartic, (g) Tri
weight , (h) Tri cube, (i) Cosine, (j) Uniform, and (k) Lapla-
cian of Gaussian
61

Y. SOH ET AL.
worst in terms of detecting true positives. All the other
kernels performed equally well except Epanechnikov
kernel where more false positives are seen. Since it is not
easy to compare the performance exactly just by visual
observation, we resort to quantitative comparison in next
section.
4.2. Quantitative Analysis
Figure. 4 sho ws the ROC curves for nine kernel func-
tions for STATIC. Horizontal axis and vertical axis cor-
respond to recall and precision respectively. Figure. 5
and Figure. 6 depict the ROC curves for nine kernel
functions for MILD and SEVERE respectively and axis
convention is the same as the one in Figure. 4. Uniform
kernel was the worst and cosine kernel seems to be the
best for all the videos. Among the others, LoG and Gaus-
sian kernels showed relatively poor performance. As we
go from STATIC to MILD and from MILD to SEVERE,
all kernels performance deteriorated due to increasing
background dynamics.
4.3. Bandwidth Analysis
Figure. 7 shows the ROC curves of different bandwidths
for each kernel function for STATIC. Bandwidths tested
were 20, 40, and 60. For all kernels bandwidth of 20
Figure 4. ROC Curves for STATIC
Figure 5. ROC Curves for MILD
Figure 6. ROC Curves for SEVERE
(a) (b)
(c)
(d) (e)
(f)
(g) (j)
(i)
Figure 7. (a) Triangular, (b)Gaussian, (c) Epanechni kov,
(d) Quartic, (e) Tri w eight, (f) Tri cube, (g) Cosine, (j) Uni-
form, and (i) Laplacian of Gaussian
62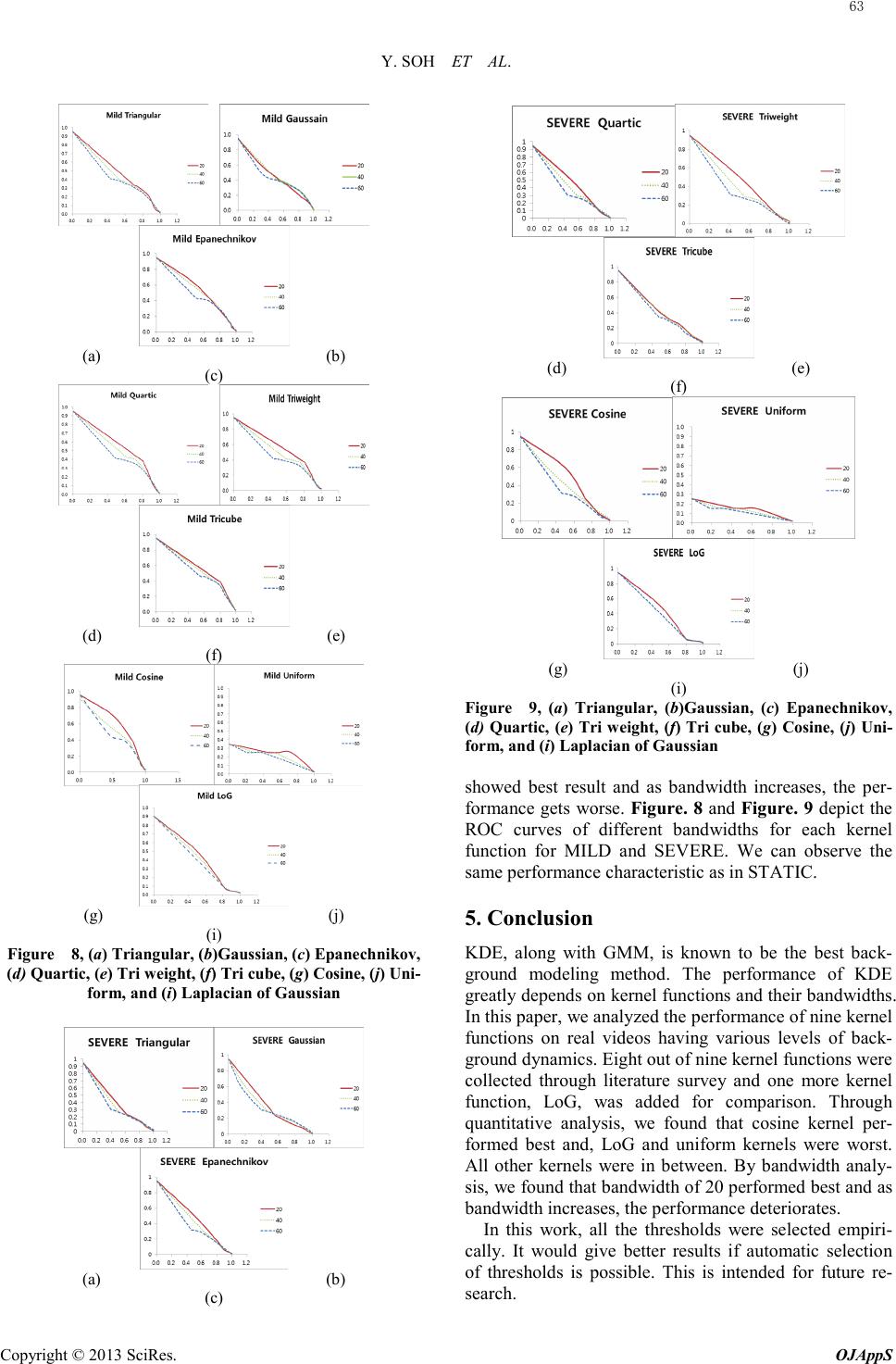

Y. SOH ET AL.
(a) (b)
(c)
(d) (e)
(f)
(g) (j)
(i)
Figure 8, (a) Triangular, (b)Gaussian, (c) Epanechnikov,
(d) Quartic, (e) Tri w eight, (f) Tri cube, (g) Cosine, (j) Uni-
form, and (i) Laplacian of Gaussian
(a) (b)
(c)
(d) (e)
(f)
(g) (j)
(i)
Figure 9, (a) Triangular, (b)Gaussian, (c) Epanechni kov,
(d) Quartic, (e) Tri w eight, (f) Tri cube, (g) Cosine, (j) Uni-
form, and (i) Laplacian of Gaussian
showed best result and as bandwidth increases, the per-
formance gets worse. Figure. 8 and Figure. 9 depict the
ROC curves of different bandwidths for each kernel
function for MILD and SEVERE. We can observe the
same performance characteristic as in STATIC.
5. Conclusion
KDE, along with GMM, is known to be the best back-
ground modeling method. The performance of KDE
greatly depends on kernel functions and their bandwidths.
In this paper, we analyzed the performance of nine kernel
functions on real videos having various levels of back-
ground dynamics. Eight out of nine kernel functions were
collected through literature survey and one more kernel
function, LoG, was added for comparison. Through
quantitative analysis, we found that cosine kernel per-
formed best and, LoG and uniform kernels were worst.
All other kernels were in between. By bandwidth analy-
sis, we found that bandwidth of 20 performed best and as
bandwidth increases, the performance deteriorates.
In this work, all the thresholds were selected empiri-
cally. It would give better results if automatic selection
of thresholds is possible. This is intended for future re-
search.
63

Y. SOH ET AL.
6. Acknowledgment
This work(Grants No. C0005448) was supported by
Business for Cooperative R&D between Industry,
Academy, and Research Institute funded by Korea Small
and M.
REFERENCES
[1] M. Piccardi, “Background subtraction techniques: a re-
view,” 2004 IEEE International Conference on Systems,
Man, and Cybernetics, 2004, pp.3099-3104
[2] Y. Benezeth, P. Jodoin, B. Emile, H. Laurent, and C.
Rosenberger,“Review and evaluation of commonly im-
plemented background subtraction algorithms,” 19th In-
ternational Conference on Pattern Recognition,
2008 ,pp.1- 4
[3] C. Wren, A. Azarbayejani, T. Darrel, and
A.Pentland,“Pfinder: real-time tracking of the human
body,” IEEE Transactions on Pattern analysis and Ma-
chine Intelligence, vol.19, no.7, 1997, pp.780-785.
[4] P. Wayne Power, Johann A. Schoonees, “Understanding
Background Mixture Models for Foreground Segmenta-
tion,” Proc. Image and Vision Computing New Zealand,
2002.
[5] A. Elgammal, R. Duraiswami, , D. Harwood, and L. Da-
vis, "Background and Foreground Modeling Using Non-
parametric Kernel Density Estimation for Visual Surveil-
lance,” Proc. of IEEE, VOL. 90, NO. 7, 2002
[6] N. Oliver, B. Rosario, and A. Pentland, “A Bayesian
computer vision system for modeling human interac-
tions,” IEEE Transactions on Pattern analysis and Ma-
chine Intelligence, vol.22, no.8, 2000, pp.831-843.
[7] W. Zucchini, Applied smoothing techniques, Part 1 Ker-
nel Density Estimation., 2003
[8] M. P. Wand ,M. C. Jones, Kernel Smoothing, Mono-
graphs on Statistics and Applied, Probability Chapman &
Hall, 1995
[9] http://mmc36.informatik.uni-augsburg.de/VSSN06_OS
64