Paper Menu >>
Journal Menu >>
 Wireless Sensor Network, 2010, 2, 683-688 doi:10.4236/wsn.2010.29082 Published Online September 2010 (http://www.SciRP.org/journal/wsn) Copyright © 2010 SciRes. WSN Weak Greedy Routing over Graph Embedding for Wireless Sensor Networks Zhigang Li, Nong Xiao Computer School, National University of Defense Technology, Changsha, Hunan, China E-mail: {lzg, nongxiao}@nudt.edu.cn Received June 11, 2010; revised July 22, 2010; accepted August 31, 2010 Abstract In this paper we classify the greedy routing in sensor networks into two categories, strong greedy routing and weak greedy routing. Most existing work mainly focuses on weak greedy routing over geographic location network or strong greedy routing over greedy embedding network. It is a difficult job and needs much cost to obtain geographic location or greedy embedding of the network. We propose a light-weight Tree-based graph embedding (TGE) for sensor networks. Over the TGE, we design a weak greedy routing protocol, TGR. TGR can archive good performance on path stretch factor and load balance factor. Keywords: WSN, Greedy routing, Graph embedding, TGR 1. Introduction Wireless sensor networks (WSN) are deployed in real-world for monitoring events and collecting data from the environment [1, 2]. The sensor node limitations in power, computation, storage and bandwidth lead the sensor network to be very different from the traditional networks, especially in the data forwarding and routing aspect. For example, in the Internet, route table can be used for data routing and forwarding, which is the core of the Internet routing protocol. The routing in wireless sensor networks, however, often adopts stateless routing protocol [3] rather than route table based routing proto- col because of the above mentioned limitations. Greedy routing is one kind of stateless routing widely used in real deployed wireless sensor networks [3,4]. The most popular greedy routing is based on geographic in- formation, which is called geographic greedy routing. In such protocol, the current node often selects the nearest node to the destination as the next hop to transmit data. The biggest challenge in geographic greedy routing is the local minimal problem, when the current node cannot find a nearer node than itself to the destination even a path existing from the current node to the destination. The local minimal problem is caused by the “hole” [5,6] or the shape irregular of the network. In order to solve this problem, two approaches are proposed. The first solution tries to remedy the greedy routing rules but still relies on the original geographic information. The face routing is a classical example of the first solution. In the face routing, when the current node cannot find the next hop node by greedy routing rules, it gives up the greedy routing but adopts face routing in order to detour the “hole”. The literature [3] proposes how to implement face routing in sensor networks by planarizing the sensor network and using right (or left) hand rule. The literature [4] concludes several different face routing protocols and proves that GFG and GOAFR + + can be used in any planar graph and are loop free protocols. On the other hand , the second solution does not give up the greedy motivation, but tries to find a new embed- ding for the network that is satisfying the greedy charac- teristic [7].A greedy embedding of an undirected graph G in a metric space (X, d) is a mapping f :V (G)→X with the following property: for every pair of distinct vertices s,tV(G) there exists a vertex u adjacent to s such that d(f(u),f(t)) < d(f(s),f(t)) [8]. Unfortunately, it is not true that every finite graph has a greedy embedding into the Euclidean plane [8]. Even if there exist such embedding into the Euclidean plane for certain finite graphs, it is a difficult work to assign such embedding to a sensor net- work in a distributed manner. The literature [7] embeds the sensor network into hyperbolic plane by constructing a spanning tree in the network. This work can achieve greedy routing over the spanning tree. But it wastes most links of the original network and cannot reach load bal- ance. Inspired by these two solutions, we classify the greedy  Z. G. LI ET AL. Copyright © 2010 SciRes. WSN 684 routing into two kinds. One is strong greedy routing, which does not give up the greedy motivation. The other one is weak greedy routing, which may give up greedy motivation when the greedy approach does not work. By this classification, the embedding approach is strong greedy routing and face routing is weak greedy routing. The existing weak greedy routing protocol solution is still based on the geographic information. As well known, it is also very difficult to obtain the geographic location information of all nodes in sensor network. In our work, we propose a new weak greedy routing method. It does not need the geographic location. It establishes a tree-based graph embedding rather than a greedy embedding. In the tree-based graph embedding, every node is assigned an interval label: [i, r]. Based on nodes labels, we design a new greedy routing algorithm TGR (Tree-based Greedy Routing). When the current node cannot find a next hop node by the greedy rule, it uses a default rule to find a next hop node. It is guaran- teed that TGR algorithm is a loop-free routing protocol. It means that by using TGR algorithm, any source can find a path to any destination, while there’s no node appears along this path twice or more. Another interesting point is that the source node can route to the destination even it only knows part of the label of the destination. By extensive evaluation, our algorithm satisfies small path stretch factor and small load balance factor. The rest of this paper is organized as follows. We dis- cuss graph labeling and graph embedding in Section 2. Section 3 illustrates the establishment of Tree-based Graph Embedding. Section 4 describes how to design weak greedy routing in TGE. Section 5 presents exten- sive simulation results that show the performance of TGR. We conclude this work in Section 6. 2. Preliminaries In this work, we take the wireless sensor network as a finite graph. We use some techniques on graph labeling and graph embedding in graph theory. 2.1. Graph Labeling Scheme A graph labeling scheme is an assignment of labels to the vertices or the edges of a graph subject to certain condi- tions [9]. There are many researches focused on such area from 1960s. The labels can be integers, integer intervals [10] or bits. There are different forms of graph labeling according different motivations, such as distance labeling, graceful labeling and harmonious labeling, etc. In our work, we only label the node and assign a unique integer pair to each node. An integer pair also can be taken as an integer interval. It can be formulated as fol- lows, L: N → N 2. 2.2. Graph Embedding Graph embedding [11,12] is a technique for map- ping a guest graph G into a host graph H in graph theory. It is defined in [12] as follows. An embedding of the graph G (the guest graph), consists of two map- pings: (1) The node-assignment function α maps the set of nodes in G one-to-one into the set of nodes in H. (2) The edge- routing function ρ assigns to each edge {u,v}E(G) a path in H that connects nodes α(u) and α(v). For sensor network, there are many researches on how to build a tree structure among the whole network. For tree structure, the node only keeps its parent information (the root has no parent) and children’s information, which are all its first hop neighbors. Firstly our work maps a shortest path tree into a sensor network. Then a labeling process is running by visiting the tree. 3. Tree-Based Graph Embedding In our work, we have the following assumptions. Firstly, a wireless sensor network is a connected graph. Secondly, the node in a wireless sensor network does not know its own and other nodes’ location information. Thirdly, we also assume that it is a static network or in a period it keeps static, which means no node will be added and no node will fail in a certain period. The establishment of TGE includes two steps. The first step is building a tree structure for the network and also counts the total number of sensors. Then the labels are assigned from the root using top-down approach at the second step. 3.1. Counting Nodes Number by Spanning Shortest Path Tree At first, a node is selected randomly as root node. Then the root node broadcasts a “HELLO” message to other node. The other node figures the shortest hop number to the root node. During this process, each node also selects one neighbor node whose hop number is less than itself as its parent node. At last a spanning shortest path tree is established in the network. After the SPT is established, every intermediate node except the leaf nodes can be seen as a root of one sub-tree. Then each leaf node initials and sends a “COUNTER = 1” message to its parent. When the parent of all leaves receives the “COUNTER = 1” message, it sends a “COUNTER = m” message to its parent, where m equals the number of its children plus 1. All the inter- mediate nodes do the same operation. At last the root can  Z. G. LI ET AL. Copyright © 2010 SciRes. WS N 685 receive a “COUNTER = n - 1” message and counts the total nodes number n of the network. During these two processes, each node only sends 2 messages at most. The first one is the “HELLO” message and the second one is the “COUNTER = i” message. But every node may receive several pieces of messages for both “HELLO” and “COUNTER = i” message. When considering transmission and receiving cost both, the cost of the whole network is (2 + d)n, where d is the average node degree of the network. 3.2. Label Assignment After the first step, the SPT is established and the root node figures out the total number of the network. Then the root node initials the label assignment process. Ini- tially, the root node sets its label in the form of a interval [1, n]. The root node also knows the nodes number of each sub-tree rooted by each of its children nodes. Sup- pose it has k children nodes C1, C2,...,Ck. Ci. count stands for the nodes number of the sub-tree rooted by Ci . The root keeps 1, the left boundary of interval [1, n], and di- vides the interval [2, n] into k sub-intervals in proportion to C1.count, C2.count, ..., Ck. count. For example, we can assign [2, C1.count + 1], [C1.count + 2,C1.count + C2. count + 1],...,[n − Ck. count + 1,n] to C1,C2 ,...,Ck sepa- rately. More generally, for the intermediate node N, if its label is [i, r] and it has l child nodes C1,C2,...,Cl. Then we can assign [i + 1,i + C1.count], [I + C1.count + 1,I + C1.count + C2.count],...,[r − Cl. count + 1, r] to C1, C2,...,Cl, the same procedure as the root node. After the label assignment process, the Tree-based Graph Embedding is also established. Figure 1 shows an example of the TGE network. In the TGE network, each node has a label [i,r], which is also an interval. We call the left boundary i as the ID of the node and r is called the range of the node. From the process of the label assignment, we can see the integer interval [i, r] of the intermediate node N with label [i, r] includes all the nodes IDs of the sub-tree rooted by N. 4. Routing Algorithms over TGE Suppose the source node1 is S: [iS, rS] and the destination is D: [iD, rD]. For the source node S, when it needs to send a packet to D, it can only get the ID of node D, such as by Hash function. There are two cases for S and D as follows, 1) Inclusion case: iD [iS, rS]. 2) Separation case: iD [iS, rS]. Fi gure 1. The TGE network and node labels. For the inclusion case, there must exist one child node C: [iC, rC] of S, s.t., iC ≤ iD ≤ rC. Then the source node S can send its data or query to C directly. But for the separation case, the source node has no such child node to be the next hop node. About the separation case, we have the following three approaches. 4.1. TBR: TGE-Based Basic Routing Algorithm It is obvious that the root node: [1,n] knows how to find any other node in the network by routing along the span- ning tree. So the basic idea for source node to deal with the separation case is sending its packet to its parent node on the tree until meeting the inclusion case. 4.2. TBHR: TGE-Based Basic Routing Algorithm with On e-Hop Information In the above basic routing, we only use the information of the spanning tree. It means that the path linking any two nodes is a path in the tree. In some cases, however, the node can get more information from other one-hop neighbors that are not its parent or children nodes. As in the figure 1, when node [7,8] wants to find node [12,12], it can find that node [11,12] covers node [12,12], then it can send its data to node [11,12] rather that to its parent node[4,8]. 4.3. TGR: TGE-Based Greedy Routing Algorithm 4.3.1. Greedy Function The greedy routing mainly focus on the Separation case iD [iS, rS] for the source node S: [iS, rS] and the destina- tion D: [iD, rD]. For the first case that iD [iS, rS], we also use the basic routing algorithm. The main task for our weak greedy routing is to designing a local monotonous function. First we give the following function ()sgn() (, )() D S D ix yr fxy xi if if SD D S ixi ixi 1The task of the routing is to find a next hop node to forward the data. When the next hop node is selected, we take it as source node. The source node means current node hereafter.  Z. G. LI ET AL. Copyright © 2010 SciRes. WSN 686 where sgn(n) = 1 when n > 0; sgn(n) = −1 when n < 0 and sgn(0) = 0. This function satisfies: f(x1,y1) < f(x2, y2) when (1) iD < x1 < x2 < iS or (2)iS < x2 < x1 < iD and y1>rS, y2 >rS. It means that f is monotonous in an open integer interval. 4.3.2. Routing Rules Firstly, we define Candidates neighbors as C = {N|N N(S), iS < iN < iD when iS < iD or iD < iN < iS when iD < iS}, N(S) stands for all neighbor nodes of S in the net- work. By greedy function, we design routing rules for Separation case as follows, 1) Greedy Rule: if C ≠ , the next hop node is the node with min{ f (iN ,rN ) > 0, N C }. 2) Default Rule: if C = , the next hop node is the source’s parent node. The greedy rule is illustrated in Figure 2. By greedy and default rules, we design TGR, TGE-based greedy routing algorithm. TRG is a weak routing algorithm, because when it can not find a next hop node it gives up the greedy rule and uses default rule instead. 5. Evaluation In this section, we evaluate the performance of our methods. The first important problem is about the length of the path connecting the source and destination pairs (S-D pairs). The load balance is another performance factor. First, we compare three algorithms on the path stretch factor. Then we compare their load balance when there are many S-D pairs. We also evaluate the usage of cross links that are not on the embedding tree. Our testing network has 500 nodes randomly scattered in a square area. The average degree is about 14. The diameter of the network is 16 hops. 5.1. Path Stretch In a connected network, any S-D pair has a shortest path connecting them. In a stateless sensor network, however, it is difficult to find the shortest path without flooding. In this evaluation, we randomly select 1000 S-D pairs, and (a) iS < iD (b) iS > iD Figure 2. Greedy rule. simulate their paths generated by TBR, TBHR and TGR respectively. In Figure 3, the X-axis stands for the length of the shortest path between S and D. Figure 3(a) plots the length of every actual routing path for TBR, TBHR and TGR. From Figure 3(b), we figure out the average length of the routing path with the same length of the shortest path. We can see that for the two nodes with distance less than 8, the average case of the TGR is shorter than the TBHR; and when the distance is less than 11, the TGR is shorter than TBR. For the two nodes with distance longer than 8, the average case of TBHR is shorter than TGR, and when the distance is longer than 11, the average case of TBR is shorter than TGR. We can see that (1) TBHR is always better than TBR, that means the one-hop information is very important; (2) when the distance is larger, the path length generated by TGR is longer than TBR and TBHR. That is because for the long distance two nodes, their path length by traveling the tree (TBR and TBHR) approximates with their shortest path length. 5.2. Load Balance In Figure 4(a), there are 1500 pairs of S-D pairs trans- missions randomly selected in the network. If a node has forwarded a packet, its load counter adds one. After the simulation, we order the nodes according to their load counter decreasingly. We compare the load counter dis- tribution about TBR, TBHR and TGR. It is obvious that there are more than 50 nodes among 500 nodes, which the load counter of TBR is about twice as the TGR. The load counter lines of TBR and TBHR are very close. After that, all three lines are smoothly and approximately. It is because in TBR and TBHR, the root and the nodes near the root should transmit more packets. In TGR, some source nodes can find their destinations by not passing the root node or the low-level nodes in the em- bedding tree, even the source and destination belong to two independent sub-trees. Figure 4(a) shows the trans- mission load from single node respect. For the whole network, we use load balance factor to metric the load performance. The load balance factor can be defined by using the variance of the packets account of all the nodes participated in the routing work, 2 1() n ii iLL n where Li is the packets account passing the node i, Li is the average packets of all nodes that have forwarded some packets, n is the total number of all nodes that have transmitted packets. If φ becomes larger, it means the load balance get worse; if φ becomes smaller, it means the load balance get better. We call φ as the load balance factor. In Figure 4(b), for the same network, we ran- 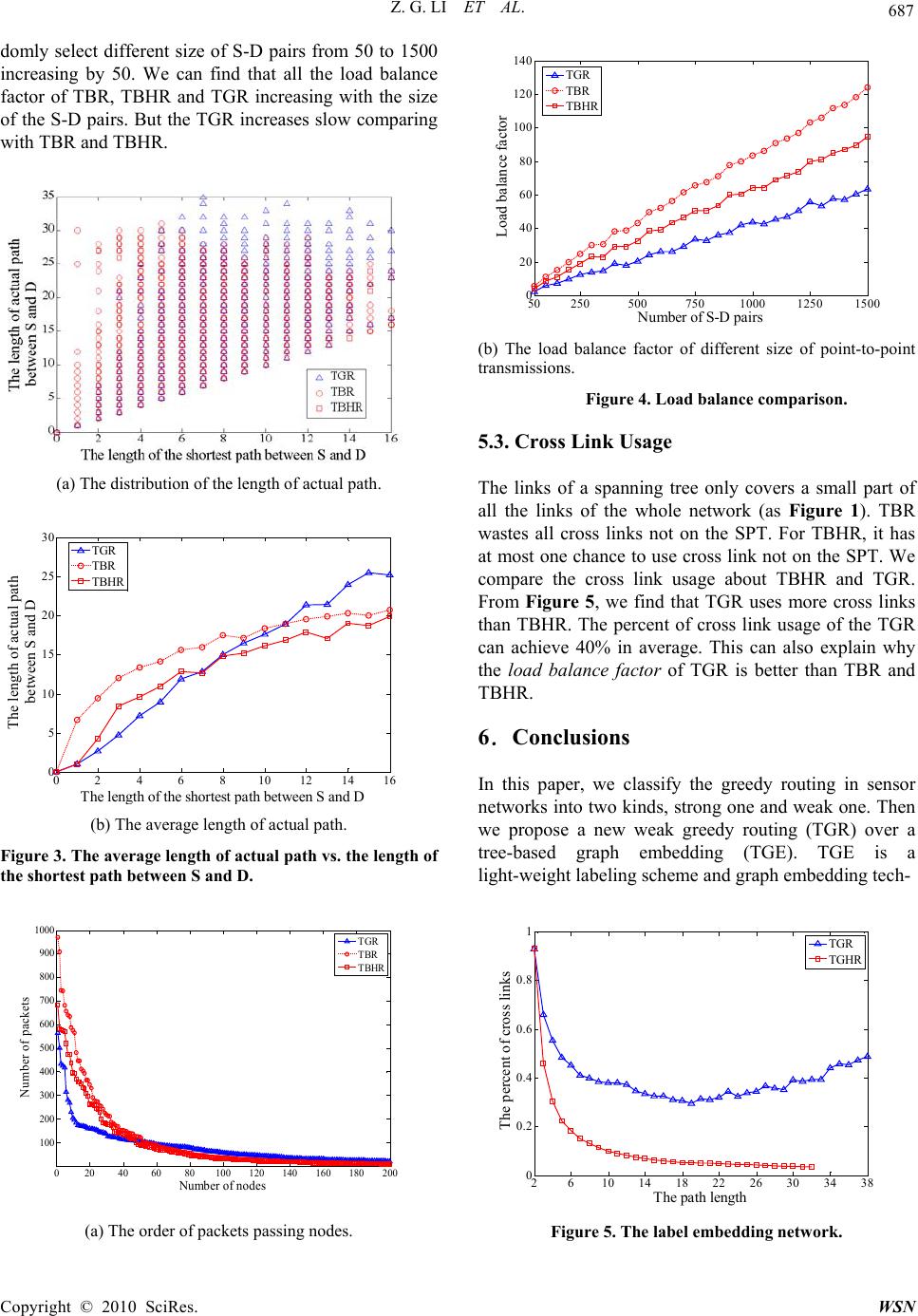 Z. G. LI ET AL. Copyright © 2010 SciRes. WS N 687 domly select different size of S-D pairs from 50 to 1500 increasing by 50. We can find that all the load balance factor of TBR, TBHR and TGR increasing with the size of the S-D pairs. But the TGR increases slow comparing with TBR and TBHR. (a) The distribution of the length of actual path. 0 24 6 810 12 14 16 0 5 10 15 20 25 30 The len g th of the shortest p ath between S and D The length of actual path between S and D TGR TBR TBHR (b) The average length of actual path. Figure 3. The average length of actual path vs. the length of the shortest path between S and D. 020 40 6080100120 140 160 180200 100 200 300 400 500 600 700 800 900 1000 Number of nodes Number of packets TGR TBR TBHR (a) The order of packets passing nodes. 50 250 500750 1000 1250 1500 0 20 40 60 80 100 120 140 Number of S-D pairs Load balance factor TGR TBR TBHR (b) The load balance factor of different size of point-to-point transmissions. Figure 4. Load balance comparison. 5.3. Cross Link Usage The links of a spanning tree only covers a small part of all the links of the whole network (as Figure 1). TBR wastes all cross links not on the SPT. For TBHR, it has at most one chance to use cross link not on the SPT. We compare the cross link usage about TBHR and TGR. From Figure 5, we find that TGR uses more cross links than TBHR. The percent of cross link usage of the TGR can achieve 40% in average. This can also explain why the load balance factor of TGR is better than TBR and TBHR. 6.Conclusions In this paper, we classify the greedy routing in sensor networks into two kinds, strong one and weak one. Then we propose a new weak greedy routing (TGR) over a tree-based graph embedding (TGE). TGE is a light-weight labeling scheme and graph embedding tech- 26 10 14 18 2226 30 3438 0 0.2 0.4 0.6 0.8 1 The path length The percent of cross links TGR TGHR Figure 5. The label embedding network.  Z. G. LI ET AL. Copyright © 2010 SciRes. WSN 688 nique. It assigns each node an integer interval. Base on nodes labels, TGR can achieve good performance in path stretch factor and load balance factor for a static con- nected network. In future network, we will study how to implement TGE and TGR in dynamic networks for re- solving nodes adding and nodes failure. Acknowledgment The research was partially supported by the Program for New Century Excellent Talents in University (NCET-08- 0145), the National Natural Science Foundation of China under Grant No.60736013. We would also like to thank the anonymous reviewers for their constructive com- ments. 7. References [1] F. Ren, H. Huang and C. Lin, “Wireless Sensor Networks,” Journal of Software, Vol. 14, No. 7, 2003, pp.1282-1291. [2] L. M. Sun, J. Z. Li, Y. Chen and H. S. Zhu, “Wireless Sensor Network, Tsinghua University Press, Beijing, 2005. [3] B. Karp and H. T. Kung, “Gpsr: Greedy Perimeter State- less Routing for Wireless Networks,” The 6th ACM An- nual International Conference on Mobile Computing and Networking, Boston, 2000, pp. 243-254. [4] H. Frey and I. Stojmenovic, “On Delivery Guarantees of Face and Combined Greedy Face Routing in Ad Hoc and Sensor Networks,” The 12th ACM Annual International Conference on Mobile Computing and Networking, Los Angeles, 2006, pp. 390-401. [5] M. Li and Y. Liu, “Rendered Path: Range-Free Localiza- tion in Anisotropic Sensor Networks with Holes,” The 13th ACM Annual International Conference on Mobile Computing and Networking, Québec, 2007, pp. 51-62. [6] X. B. Wu, G. Chen and K. D. Sajal, “Avoiding Energy Holes in Wireless Sensor Networks with Non-uniform Node Distribution,” IEEE Transactions on Parallel and Distributed Systems, Vol. 19, No. 5, May 2008, pp. 710- 720. [7] A. Cvetkovski and M. Crovella, “Hyperbolic Embedding and Routing for Dynamic Graphs, The 28th Conference on Computer Communication, Rio de Janeiro, Brazil, April 2009, pp.1647-1655. [8] C. Papadimitriou and D. Ratajczak, “On a Conjecture Related to Geometric Routing,” Theoretical Computer Science, Vol. 344, No. 1, 2005, pp. 3-14. [9] A G. Joseph, “A Dynamic Survey of Graph Labeling,” The Electronic Journal of Combinatorics, Vol. 16, 2009, pp. 1-219. [10] J. V. Leeuwen and B. Tan, “Interval Routing,” Computer Journal, Vol. 30, 1987, pp. 298-307. [11] J. Newsome and D. Song, “Gem: Graph Embedding for Routing and Datacentric Storage in Sensor Networks without Geographic Information,” The 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, 2003, pp. 76-88. [12] A. L. Rosenberg and L. S. Heath, “Graph Separators, with Applications,” Kluwer Academic/Plenum Publishers, Norwell, Massachusetts, 2001 |

