iBusiness, 2010, 2, 218-222
doi:10.4236/ib.2010.23027 Published Online September 2010 (http://www.SciRP.org/journal/ib)
DCC and Analysis of the Exchange Rate and the
Stock Market Returns’ Volatility: An Evidence
Study of Thailand Country
Wann-Jyi Horng, Ching-Huei Chen
Department of Hospital and Health Care Administration, Chia Nan University of Pharmacy & Science, Tainan, China.
Received June 4th, 2010; revised July 9th, 2010; accepted August 10th, 2010.
ABSTRACT
This paper studies the relatedness and the model construction of exchange rate volatility and the Thailand’s stock mar-
ket returns. Empirical results show that we can construct a bivariate IGARCH (1, 1) model with a dynamic conditional
correlation (DCC) to analyze the relationship of exchange rate volatility and Thailand’s stock market returns. The av-
erage estimation value of the DCC coefficient for these two markets equals to –0.1650, this result indicates that the
exchange rate volatility negatively affects the Thailand’s stock market. Empirical result also shows that there do not
exist the asymmetrical effect on the Thailand’s exchange rate and Thailand’s stock markets. And the Japan’s stock re-
turn volatility truly affects the variation risks of the Thailand stock market. Based on the viewpoint of DCC, the bivari-
ate IGARCH (1, 1) model with a DCC has the better explanation ability compared to the traditional bivariate GARCH
(1, 1) model.
Keywords: Four Quadrant (4Q) Converter, Interlacing, Traction Systems, Power Quality Analysis
1. Introduction
We know that Thailand belongs to the Buddhism country.
And Thailand is also a famous scenic spot of travel. Be-
sides, Thailand is also one of Association of South-east
Asian Nations in the global economical financial system
and also has been very influential in the global economy.
We also know that the relationships between stock prices
and foreign exchange rates are studied of numerous
economists, because they both play crucial roles in influ-
encing the development of a country’s economy. A study
of the exchange rates affects the stock returns, for exam-
ple, Kearney [1] found that the exchange rate volatilities
in Canada and Ireland had a significance influence on
their stock market volatilities. Besides, we also can refer
to, for example, the papers of Bollerslev [2], Nieh and
Lee [3], and Yang and Doong [4]. Therefore, the rela-
tionships of the foreign exchange rates and the stock
market will also become an important topic. In this paper,
we will consider the factors of the foreign exchange rates
to discuss it on the stock market’s influence. An evidence
study of the Thailand’s stock market is considered. We
also know that Japan is one of eight big industrialized
countries in the global economical financial system. In
the year 2006, for example, the turnover of the Japan’s
Tokyo stock market achieves to US5,497 billion, which
is only inferior to the New York and London stock ex-
changes. Therefore, we are also considered the influence
factor of Japan’s stock market in Thailand.
In this paper, the Student’s t distribution is adopted and
the maximum likelihood algorithm method of BHHH [5]
is used to estimate the model’s unknown parameters. The
programs of RATS and EVIEWS are used in this paper.
This paper is organized as follows. Section 2 states the
data characteristics. Section 3 presents the asymmetric
test of the bivariate GARCH model. Section 4 introduces
the proposed models of DCC and GARCH. Section 5
presents the empirical results, and ends with Section 6 of
conclusions.
2. Data Characteristics
2.1. Basic Statistics and Trend Charts
In the sample selection, this research uses the Thailand
stock index (t THAIL ), NK-225 stock index (t JAPANL ) and
the closed price of the Thailand’s exchange rate (t
THER )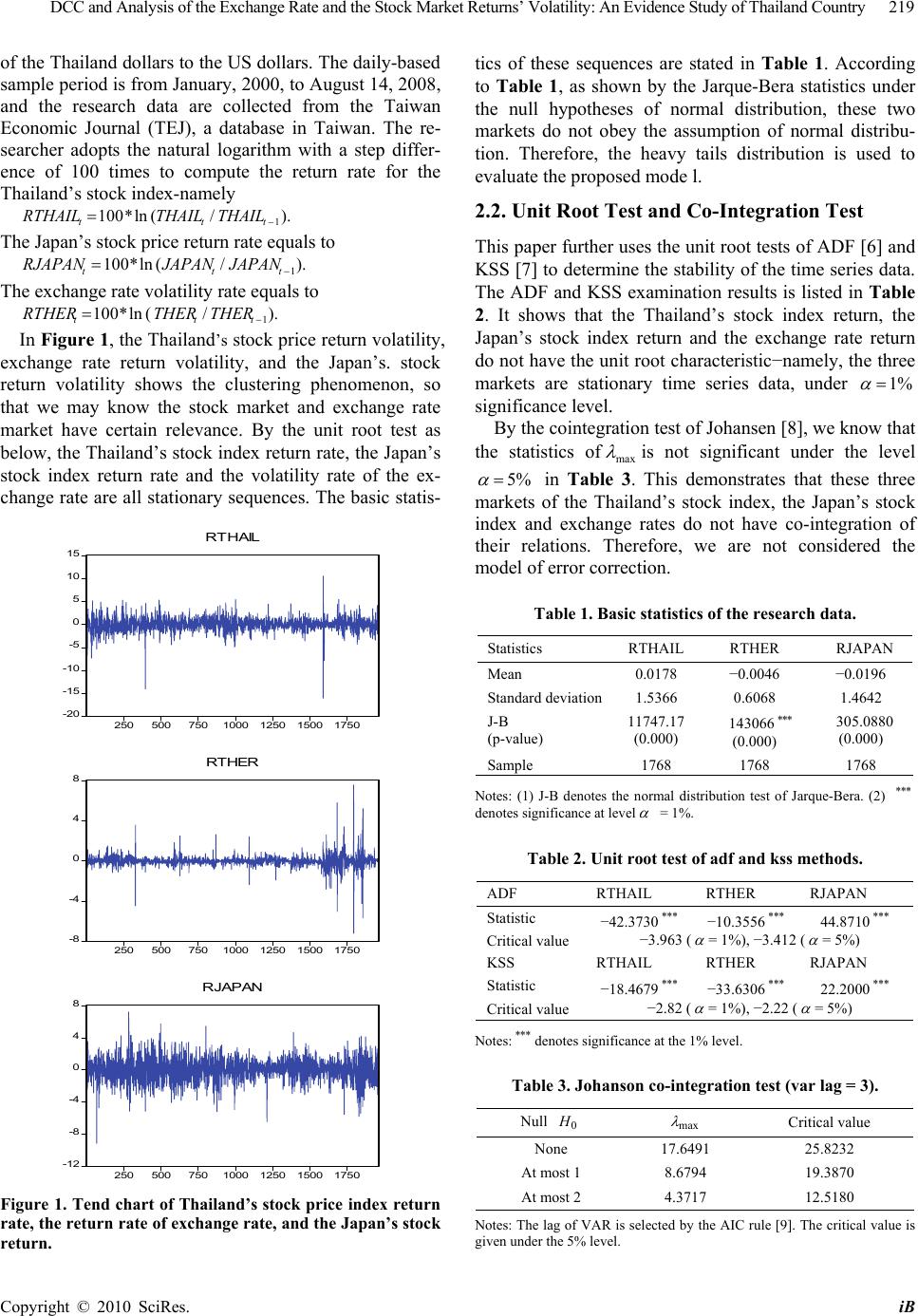

DCC and Analysis of the Exchange Rate and the Stock Market Returns’ Volatility: An Evidence Study of Thailand Country
219
of the Thailand dollars to the US dollars. The daily-based
sample period is from January, 2000, to August 14, 2008,
and the research data are collected from the Taiwan
Economic Journal (TEJ), a database in Taiwan. The re-
searcher adopts the natural logarithm with a step differ-
ence of 100 times to compute the return rate for the
Thailand’s stock index-namely
). / ( ln*100 1  ttt THAILTHAILRTHAIL
The Japan’s stock price return rate equals to
). / ( ln*1001  ttt JAPANJAPANRJAPAN
The exchange rate volatility rate equals to
). / ( ln*100 1  ttt THERTHERRTHER
In Figure 1, the Thailand’s stock price return volatility,
exchange rate return volatility, and the Japan’s. stock
return volatility shows the clustering phenomenon, so
that we may know the stock market and exchange rate
market have certain relevance. By the unit root test as
below, the Thailand’s stock index return rate, the Japan’s
stock index return rate and the volatility rate of the ex-
change rate are all stationary sequences. The basic statis-
-20
-15
-10
-5
0
5
10
15
250 500 7501000125015001750
RT H
A
IL
-8
-4
0
4
8
250 500 7501000125015001750
RTHER
-12
-8
-4
0
4
8
250 500 7501000125015001750
RJAPAN
Figure 1. Tend chart of Thailand’s stock price index return
rate, the return rate of exchange rate, and the Japan’s stock
return.
tics of these sequences are stated in Table 1. According
to Table 1, as shown by the Jarque-Bera statistics under
the null hypotheses of normal distribution, these two
markets do not obey the assumption of normal distribu-
tion. Therefore, the heavy tails distribution is used to
evaluate the proposed mode l.
2.2. Unit Root Test and Co-Integration Test
This paper further uses the unit root tests of ADF [6] and
KSS [7] to determine the stability of the time series data.
The ADF and KSS examination results is listed in Table
2. It shows that the Thailand’s stock index return, the
Japan’s stock index return and the exchange rate return
do not have the unit root characteristic−namely, the three
markets are stationary time series data, under %1


significance level.
By the cointegration test of Johansen [8], we know that
the statistics ofmax

is not significant under the level
%5


in Table 3. This demonstrates that these three
markets of the Thailand’s stock index, the Japan’s stock
index and exchange rates do not have co-integration of
their relations. Therefore, we are not considered the
model of error correction.
Table 1. Basic statistics of the research data.
Statistics RTHAIL RTHER RJAPAN
Mean 0.0178 −0.0046 −0.0196
Standard deviation1.5366 0.6068 1.4642
J-B
(p-value)
11747.17
(0.000)
143066***
(0.000)
305.0880
(0.000)
Sample 1768 1768 1768
Notes: (1) J-B denotes the normal distribution test of Jarque-Bera. (2) ***
denotes significance at level

= 1%.
Table 2. Unit root test of adf and kss methods.
ADF RTHAIL RTHER RJAPAN
Statistic −42.3730 *** −10.3556 *** 44.8710***
Critical value −3.963 (

= 1%), −3.412 (

= 5%)
KSS RTHAIL RTHER RJAPAN
Statistic −18.4679 *** −33.6306 *** 22.2000***
Critical value −2.82 (

= 1%), −2.22 (

= 5%)
Notes: *** denotes significance at the 1% level.
Table 3. Johanson co-integration test (var lag = 3).
Null 0 H max  Critical value
None 17.6491 25.8232
At most 1 8.6794 19.3870
At most 2 4.3717 12.5180
Notes: The lag of VAR is selected by the AIC rule [9]. The critical value is
given under the 5% level.

DCC and Analysis of the Exchange Rate and the Stock Market Returns’ Volatility: An Evidence Study of Thailand Country
220
2.3. ARCH Effect Test
Based on the Formulas (1) and (2) as below, we uses the
methods of LM test [10] and F test [11] to test the condi-
tionally heteroskedasticity phenomenon. In Table 4, the
results of the ARCH effect test show that these two mar-
kets have the conditionally heteroskedasticity phenome-
non exists. This result suggests that we can use the
GARCH model to match and analyze it. The detail is
omitted here.
3. Asymmetric Test of the Bivariate
IGARCH Model with a DCC
The bivariate IGARCH (1, 1) model with a DCC can be
constructed in the next section. The asymmetric test
methods [12] are used the following two methods as:
negative size bias test and joint test.
Table 5 asymmetrically examines the result for the
Thailand’s stock market as: 1) The positive size bias test
does not reveal (

= 10%). 2) The joint test does not
reveal (

= 10%). Table 5 asymmetrically examines the
result for the exchange rate market as: 1) The positive
size bias test does not reveal (

= 10%). 2) The joint test
does not reveal (

= 10%).
4. Proposed Model
A dynamic conditional correlation (DCC) and the bivari-
ate GARCH (1, 1) model with an Japan’s. stock market
factor is proposed in this section, its model may be ex-
pressed as
 1110 tt RTHERRTHAIL


ttt aRJAPANRTHAIL ,131121  


(1)
Table 4. Arch effect test (lag = 15).
RTHAIL Engle LM test Tsay F test
Statistics 316.4800 *** 7.5925***
(p-value) (0.0000) (0.0000)
RTHER Engle LM test Tsay F test
Statistics 504.9780 *** 20.4977***
(p-value) (0.0000) (0.0000)
Notes: ** denotes significance at the level 5% and ***denotes significance at
level

= 1%.
Table 5. Asymmetric test of the bivariate igarch.
Asymmetric test Positive size bias test Joint test
F statistic 0.2893 0.4174 RTHAIL
(p-value) (0.5907) (0.7405)
Asymmetric test Positive size bias test Joint test
F statistic 0.5850 0.6530
RTHER
(p-value) (0.4444) (0.5810)
Notes: p-value <

denotes significance (

= 5%).



1110tt RTHERRTHER


ttt aRJAPANRTHAIL,232121




(2)
)/)2(,0(~),(,2,1
'

tvttt HTaaa 


(3)
t
h,11 = 10

+ 1,1111
2
1,111 tt ha
 + 2
11 t
RJAPAN  (4)
t
h,22 = 20

+ 1,2221
2
1,221 ttha
 + 2
1,12t
a  (5)
1,221,111,21,12110 /  tttttt hhaaq

)1 )( (exp / )1)( (exp 


ttt qq

(6)
tttt hhh ,22,11,12
  (7)
where )/ )2( ,0( vHvT tv 

denotes the bivariate Student’s t
distribution, its mean is equal to 0 and its covariance ma-
trix is equal tovHvt / )2(

, and
v
is the degree of free-
dom. The DCC and the bivariate GARCH model can also
refer to the papers of Engle [13] and Tse and Tsui [14].
5. Empirical Results
From the asymmetric test results in Table 5, we can use
the symmetric GARCH model to analyze the exchange
rate and the Thailand’s stock markets. Table 6 shows the
estimate results for the Thailand’s stock index return and
exchange rate volatility rate by the DCC and the bivariate
IGARCH (1, 1) model with a factor of Japan’s stock
market. Empirical result shows that the Thailand’s stock
market return receives the previous one period’s influ-
ence of the exchange rate volatility. Empirical result also
indicates that the Thailand’s stock market return receives
the previous one period’s influence of the Thailand’s
stock return volatility. The Thailand’s stock market re-
turn also receives the previous third period’s influence of
the Japan’s stock return volatility. Empirical result also
shows that the exchange rate market return receives the
previous one period’s influence of the exchange rate re-
turn volatility. Empirical result also indicates that the
exchange rate market return receives the previous one
period’s influence of the Thailand’s stock return volatility.
The exchange rate market return does not receive the
previous third period’s influence of the Japan’s. stock
return volatility. Regarding the degrees of freedom of the
Student’s distribution estimated value, it is 3.859, which
under the 1% significance level is significant.
Empirical result also shows that the variation risks of
the exchange rate and the Thailand’s stock return volatil-
ity do have the different variation risks. Besides, the like-
lihood ratio test is also supported the proposed model
under the Japan and non-Japan stock market factor. The
details are omitted in this paper. And proposed model
conforms to the parameters of the IGARCH and GARCH
model’s supposition. From the above results, we can re-

DCC and Analysis of the Exchange Rate and the Stock Market Returns’ Volatility: An Evidence Study of Thailand Country
221
Table 6. Asymmetric test of the bivariate igarch.
Parameter 0
 11
 21 
Coefficient 0.0419 −0.0961 0.0599
(p-value) (0.1054) ( 0.0302) (0.0104)
Parameter 1  0
 11

Coefficient 0.0722 −0.0048 −0.0541
(p-value) (0.0001) (0.4632) (0.0257)
Parameter 21  2 
Coefficient −0.094 −0.0006
(p-value) (0.0000) (0.8952)
Parameter 10
 11  11 
Coefficient 0.1457 0.1839 0.7921
(p-value) ( 0.0001) (0.0000) (0.0000)
Parameter 1
 20  21 
Coefficient 0.0240 0.0187 0.3156
(p-value) (0.0914) (0.0000) (0.0000)
Parameter 21
 2 
Coefficient 0.6467 0.00001
(p-value) (0.0000) (0.9870)
Parameter 0
 1  2 
Coefficient −0.6615 −2.0047 0.0180
(p-value) (0.0000) (0.0045) (0.2685)
Parameter t


Coefficient −0.1650 3.8590
(p-value) (0.0000) (0.1914)
Notes: p-value <

denotes significance (

= 1%,

= 5%,

= 10%);

is the significance level.
alize that the exchange rate and the Thailand’s stock
market return’s volatility do not have an asymmetrical
effect. The square item of the Japan’s stock return also
affects the variation risk of the Thailand stock market.
But the error square item of the Thailand’s stock return
does not affect the variation risk of the exchange rate
market. Therefore, the DCC and the bivariate IGARCH
(1, 1) model with a Japan’s stock market factor might
capture the exchange rate and the Thailand’s stock mar-
ket return’s volatility process.
To test the inappropriateness of the DCC and the
bivariate IGARCH (1, 1) model with an U.S. stock mar-
ket factor, the test method of Ljung & Box [15] is used to
examine autocorrelation of the standard residual error.
This model does not show an autocorrelation of the stan-
dard residual error, the details are omitted. Based on the
paper of Engle [13], the DCC and the bivariate IGARCH
(1, 1) model with a factor of Japan’s stock market are
more appropriate.
6. Conclusions
The empirical results present that the volatility process do
not have an asymmetrical in the exchange rate and
Thailand’s stock markets. The empirical results also
show that the exchange rate volatility rate truly has an
affect on the Thailand’s stock market return rate’s vola-
tility. However, the proposed model is different from the
traditional model of the bivariate GARCH. Based on the
viewpoint of DCC, the DCC and the bivariate IGARCH
model have a better explanatory ability compared to the
traditional bivariate GARCH model.
REFERENCES
[1] C. Kearney, “The Causes of Volatility in a Small, Interna-
tionally Integrated Stock Market: Ireland, July 1975 -
June 1994,” Journal of Financial Research, Vol. 21, No.
4, 1998, pp. 85-104.
[2] T. Bollerslev, “Modeling the Coherence in Short-Run
Nominal Exchange Rates: A Multivariate Generalized
ARCH Model,” Review of Economics and Statistics, Vol.
72, No. 3, 1990, pp. 498-505.
[3] C. C. Nieh and C. F. Lee, “Dynamic Relationship be-
tween Stock Prices and Exchange Rates for G-7 Coun-
tries,” The Quarterly of Economics and Finance, Vol. 41,
No. 3, 2001, pp. 477-490.
[4] S. Y. Yang and S. C. Doong, “Price and Volatility Spill-
overs between Stock Prices and Exchange Rates: Empirical
Evidence from the G-7 Countries,” International Journal of
Business and Economics, Vol. 3, No. 2, 2004, pp. 139-153.
[5] E. K. Berndt, B. H. Hall, R. E. Hall and J. A. Hausman,
“Estimation and Inference in Nonlinear Structural Mod-
els,” Annals of Economic and Social Measurement, Vol. 3,
No. 4, 1974, pp. 653-665.
[6] D. A. Dickey and W. A. Fuller, “Distribution of the Esti-
mators for Autoregressive Time Series with a Unit Root,”
Journal of the American Statistical Association, Vol. 74,
No. 366, 1979, pp. 427-431.
[7] G. Kapetanios, Y. Shin and A. Snell, “Testing for a Unit
Root in the Nonlinear STAR Framework,” Journal of
Econometrics, Vol. 112, No. 2, 2003, pp. 359-379.
[8] S. Johansen, “Estimation and Hypothesis Testing of Coin-
tegration Vector in Gaussian Vector Autoregressive Mod-
els,” Econometrica, Vol. 59, No. 6, 1991, pp. 1551-1580.
[9] H. Akaike, “Information Theory and an Extension of the
Maximum Likelihood Principle,” 2nd International Sym-
posium on Information Theory, B. N. Petrov and F. C.
Budapest, Eds., Akademiai Kiado, Budapest, 1973, pp.
267-281.
[10] R. F. Engle, “Autoregressive Conditional Heteroskedas-
ticity with Estimates of the Variance of United Kingdom
Inflation,” Econometrica, Vol. 50, No. 4, 1982, pp. 987-
1007.
[11] R. S. Tsay, “Analysis of Financial Time Series,” John
Wiley & Sons, Inc., New York, 2004.
[12] R. F. Engle and V. K. Ng, “Measuring and Testing the
Impact of News on Volatility,” Journal of Finance, Vol.
48, No. 5, 1993, pp. 1749-1777.
[13] R. F. Engle, “Dynamic Conditional Correlation - A Sim-

DCC and Analysis of the Exchange Rate and the Stock Market Returns’ Volatility: An Evidence Study of Thailand Country 222
ple Class of Multivariate GARCH Models,” Journal of
Business and Economic Statistics, Vol. 20, No. 3, 2002,
pp. 339-350.
[14] Y. K. Tse and A. K. C. Tsui, “A Multivariate GARCH
Model with Time-Varying Correlations,” Journal of
Business & Economic Statistics, Vol. 20, No. 3, 2002, pp.
351-362.
[15] G. M. Ljung and G. E. P. Box, “On a Measure of Lack of
Fit in Time Series Models,” Biometrika, Vol. 65, No. 2,
1978, pp. 297-303.