Journal of Software Engineering and Applications, 20 12, 5, 30-35
doi:10.4236/jsea.2012.512b007 Published Online December 2012 (http://www.SciRP.org/journal/jsea)
Reliable Multi-path Routing in Selfish Networks with
Hidden Information and Actions
Gang Peng, Mingrui Zou, Sammy Chan*
Departmentof Electronic Engineering, City University of Hong Kong, Hong Kong SAR, China.
Received 2012
ABSTRACT
In this paper, we propose a novel game-theoretical solution to the multi-path routing problem in wireless ad hoc net-
works co mprising selfis h node s with hidd en infor mation and a ctions. B y incorpora ting a suitable traffic allo catio n poli-
cy, the proposed mechanism results in Nash equilibria where each node honestly reveals its true cost, and forwarding
subgame perfect equilibrium in which each node does provide forwarding service with its declared service reliability.
Based on the generalised second price auction, this mechanism effectively alleviates the over-payment of the
well-kno wn VCG mechanism. The effectiveness of this mechanism will be shown through simulati ons.
Keywords: Wireless ad hoc network; non-cooperative networks; hidden information; hidden action; mechanism design;
GSP auction
1. Introduction
Wireless ad hoc networks consist of a set of autonomous
nodes distributed in a certain area, and do not have a
central coordinator to support communication among the
nodes. Wireless devices rely on each other to forward
packets to the destinatio n. Initiall y, protocol design often
assumed that nodes would always follow the protocol.
These kinds of design worked well because such wireless
devices were usually owned by a single entity and were
supposed to cooperate with each other. With great ad-
vancement of mobile communication and computing,
more and more small and convenient mobile devices,
such as smart phones and tablet PCs, come into everyday
life. Wireless ad hoc networks can possibly be formed by
these devices owned by different individuals. Due to li-
mitations of memory, energy supply and computing re-
sources, such devices may behave selfishly and do not
follow the protocol. This results in non-cooperative net-
works in which each node relies on other nodes to for-
ward its packets and yet is not willing to spend its own
resources to forward packets for other nodes.
To ensure normal operation in non-cooperative wire-
less networks, it requires selfish nodes to participate in
the routing protocol to establish available paths and for-
ward packets if it is along a chosen path to a destination
[18]. Since selfish nodes are mainly interested in max-
imizing their own payoffs, one common approach to deal
with them is to design an appropriate payment mechan-
ism to reward cooperation. That is, if a cooperating node
receives a payment more than its expended cost in for-
warding a packet, then it is likely to follow the routing
protocol and forward packets for other nodes. However,
an important issue of this approach is to ensure that each
node hone stly repo rts its cost expenditure in forwarding a
packet, otherwise, traffic sources will be asked to make
unrealistic payments. In many literatures [2,13,14], me-
chanis ms were designed for soliciting the truthful cost
declaration from selfish nodesso that a certain optimal
routing structure could be bui lt to connect a so urce node
and a destination node. The problem can be modeled as a
hidden information game. In addition, another important
issue is to ensure that intermediate nodes indeed forward
data packets when they are asked to [17]. Unfortunately,
as shown in [18], no dominant strategy solution exists in
which every node always forwards others’ packets.
When packet loss occurs dur ing for wardi ng, i t is dif ficult
for other nodes to distinguish whether a failure is due to
natural hazard, or due to intentionally dropping by a node.
Even if the protocol deploys monitoring mechanism to
allow the senders or the receivers to ascertain the loca-
tion of the failure, they may still be unable to attribute
the causes of failure to either the deliberate action of the
intermediate node, or some external factors beyond the
contr ol of the no de, suc h as ne twork co ngestion, channe l
interference, or data corruption. This problem is referred
to as the hidden action problem.
The VCG payment mechanism has been applied in
single-path routing [3,5,6,15,16], and multi-path routing
*Corresponding author.

Reliable Multi-path Routing in Selfish Networks with Hidden Information and Actions
31
[5] scenarios to deal with hidden information and hidden
actions. However, VCG suffers from the inevitable
over-payment problem [4,10]. Efforts to alleviate this
problem have been made in single-path routing scenario
[12]. A game method proposed in [5,16] stimulates co-
operation from intermediate nodes to overcome the hid-
den-action problem with hidden information. They
mainly considered the single-path scenario. In [8,9], we
assumed that all links and nodes are reliable, and have no
hidden action. The generalised second price (GSP) auc-
tion in multi-path routing was proposed to d eal wit h hi d-
den information of selfish nodes. In this paper, we will
extend the G SP a uction in mu lti-pat h routi ng to take i nto
account more complex conditions such as hidden action
of a node. We assume that the link failures are indepen-
dent among different links, and aim to design protocols
that can eliminate the hidden action without using addi-
tional monitoring scheme. As discussed in [8,9], al-
though GSP achieves lo wer over-pa yment than VCG, its
existing form used in Internet advertising does not guar-
antee each node to reveal its true cost. Therefore, we also
need to design a mechanism which results in Nash equi-
libria for all nodes to behave honestly.
The remainder of this paper is organized as follows.
Section 2 discusses the abstracted network representation
and system model. Section 3 builds the mechanism and
designs the algorithm that can efficiently deal with the
hidden action and hidden information problem and en-
sure reliable multi-path routing in the link layer. Section
4 evaluates their effectiveness through simulations. Sec-
tion 5 concludes this paper.
2. System Model
2.1. Network Model
A wireless network is formed by a finite number of
nodes, denoted by V = {1, 2,...,n}. The existence of the
directed edge (i, j) ∈E between node i and node j is de-
pendent on the transmission power. We assume that each
node i has a set Ti of discrete transmission power levels.
For any i, j∈V, there is a minimum power level Tij at
which node i could transmit packets to node j. If Tij≤
max(Ti), then we say node j is reachable from node i. In
this way, the network could be represented by a weighted
directed graph G = {V, E, W}, where W is the set of
weights representing the cost on each edge.
Each l ink (i, j) ∈E is assi gned an inher ent val ue η(i, j)
∈ [0, 1], denoting the reliability of the link (i, j). The
reliability of a link means the probability of decoding the
packet correctly when node i has sent a packet through
the wireless channel to node j. In other words, node j will
receive the data correctly with probability η(i, j) due to
possible corruption by interference, after node i sends
data to node j. We assume that η(i, j) is public informa-
tion i n this paper.
Each node i∈V is assigned an inherent value γi∈ [0, 1],
indicating the service reliability that a data packet will be
successfully forwarded by i if a path includ ing i i s chosen
for packet forwarding. In other words, node j will receive
the data correctly with probability γiif the link (i,j) is
completely reliable, when node ishould forward data to
node j. We assume that γi is private for each node i. Node
i can choose to declare this private information correctly
or incorr e c tly in or derto maximize its o wn utility.
For convenience, we denote δ(i, j)= γi · η(i, j) as the
value of the corresponding service from node i to node j.
We consider implementing a routing protocol that will
reliably route data from a source node S to a target node
D through multiple paths. Such a routing protocol with
selfi sh part icipati ng nodes co mpri ses of the ro uting sta ge
and forwarding stage, which are modelled as routing
subgame and forwarding subgame [18].
2.2. Least Cost Path Construction
The player set of this multi-path routing game are the
intermediate nodes. We assume each intermediate node
incurs a per-packet cost for forwarding traffic with the
corresponding service reliabilityγi, and thi s cost a nd γiare
private to itself. The reliable minimum cost multi-path
routing pro blem is to find a set of least cost p aths (LCPs)
connecting S and D such that the expected total cost
spent by all nodes (including the retransmissions) is mi-
nimized, for the g iven probabilities δ(i, j)= γi ·η(i, j).
When the link layer reliability is implemented, it means
that the retransmission is completed by the upstream
node till a packet is successfully received by the down-
stream node. Consider a path P connecting the set of
nodes {a1,a2,...,ah} wherea1is the so urce a ndah is the des -
tination, respectively. The expected cost of sending a
packet through P, ε(CP ), is given by
∑
−
=+
+
=
1
1),(
1
.
),(
1
)(
1
h
taa
tt
P
tt
c
aa
C
δ
ε
(1)
Here, 1/δ(at,at+1) is the expected number of total trans-
missions over link(at,at+1) including the initial trans-
mission and all retransmissions,
c
(at,at+1) is the cost of
sending a packet thro ugh l ink (at,at+1).
For the sake of simplicity, we assume in this pa per that
there is no collusion among the nodes. In the route dis-
covery process, each node declares a cost for an outgoing
link along with service reliability. Note that the declara-
tion may not be honest. After obtaining all the link in-
formation and constructing the network graph, the
routing protocol orders the node-disjoint paths as the
reliable LCP candidates according to the expected cost of
each path. That is, after path ordering, ε(Ci) <ε(Cj) if i<j,
where ε(Ci) is the expected cost of LCPi.

Reliable Multi-path Routing in Selfish Networks with Hidden Information and Actions
32
2.3. System Objective
Assume that the first mLCP candidates are selected for
packet forwarding. A fraction of data traffic fiwill be
forwarded through LCPi. The per-packet payment is cal-
culated according to the routing decision, forwarding
action and the bids placed by intermediate nodes. The bid
of each intermediate node is kept confidential b y encr yp-
tion and can only be exposed to the destination and
source nodes. Once the route discovery process is fi-
nished, nodes cannot change their bids before the trans-
mission is completed or rerouting is triggered. Therefore,
we model this auction as a simultaneous-move, one-shot
strategic game.
Following the definition in game theory [7], node i’s
per-packet payoff or utility uiis given by
,
iii
cpu
−= (2)
where ciis node i’s cost and piis the pa yment mad e by the
source to node i.
While it is obvious that e ach intermediate node i’s ob-
jective is to maximize its utility by giving a proper bid,
the goal of the entire system is to minimize the total
transmission cost by allocating proper
traffic among the m paths, subject to certain constraints
{P(n)}, which represent a set of policies to be discussed in
the follo wi ng section.
2.4. Policy Enhancement
In the formulation presented above, the constraints rep-
resent a set of policies {P(n)}. Such policies are an im-
portant part of our mechanism design. The basic policies
are as follows:
P(1) : Since we consider multi-pa th r out in g i n thi s paper,
naturally, the number of selected LCP candidates mis
larger than one, but less than the total number of LCP
candidates between the source and destination.
P(2) : The fractions of data traffic carried by different
selected LCP satisfy the conditions
∑=
=
m
ii
f
1
1
and
f1>f2> ··· >fm> 0. The first condition follows directly
from the fact that all packets need to be forwarded to the
destination. Moreover, we emphasize that
i∀
, fi>0 since
any fi=0 will reduce m. Also, the fact that the fractions of
traffic allocated to the mLCP candidates appear in des-
cending ord er is compatible to the entire syste m’s goa l o f
minimizing total cost, since LCP iwith larger i tends to
introduce higher cost per packet.
P(3): For any p<q, we require [ε(Cp+1) −ε(Cp)]fp>
[ε(Cq+1) −ε(Cp)]fq> [ε(Cq+1) −ε(Cq)]fq.This policy governs
how traffic are allocated among the m LCPs. The first
inequality[ε(Cp+1) −ε(Cp)]fp> [ε(Cq+1) −ε(Cp)]fqsays that a
player on a path with les s total cost tends to have a better
utility than one on a path with larger total cost. The
second inequality [ε(Cq+1) −ε(Cp)]fq> [ε(Cq+1)
−ε(Cq)]fqsays that by overbidding to go from a path with
less total cost to one with larger total cost, a player can-
not increase its utility. As we will see later , this condition
guarantees a truth-telling node’s utility if some other
nodes are trying to game the routing protocol.
3. Reliable Multi-path Routing with GSP
Auction
3.1. Payment Me ch ani sm Design
A sel fish node has certain private information such as it s
service cost and the service reliability. Thus, the actions
taken by a selfish node are 1) declaring whether it can
provid e suc h s ervices and 2 ) pr oviding the tr uthful tel ling
of service cost and what kind of forwarding service. The
main goal of this routing scheme (composed of routing
subgame and forwarding subgame) is then to ensure that
every selfish node fulfills its declared service cost and
forwarding service.
We design GSP mechanism to calculate the payment.
The objective of such a mechanism is to stimulate the
rational pla yers being honest without hurtin g their utility.
In the link layer multi-path reliable routing game, GSP
per-packet payment only considers the service cost and
service reliability of other nodes on LCPk(excluding itse lf)
and LCPk+1, and i s given by
),(
)()(
]
),(
)([)(
1
1
,
kk
i
kkk
k
k
kk
i
kkk
GSP
ki
ji
c
CfC
f
f
ji
c
CfC
p
k
k
δ
εε
δ
εε
+−=
−−
=
+
+
(3)
δ(ik,jk)is the link reliability asδ(ik,jk)=γik· η(ik,jk), and ε(Ck)
is the expected cost of LCPkpath calculated by Equation
(1).
Although GSP achieves lower over-payment than
VCG (which will be sho wn in Sectio n 4.2), GSP auction
has an unpleasant flaw that generally it does not have any
truth-telling equilibrium [1,11], where each node truth-
fully reveals its private type. In our mechanism design,
we eliminate this flaw by adding the polices discussed in
Section 2.4 which control the tr a ffic alloc a tion among the
selected LCP candidates.
3.2. Algorithms
First, we design Algor ithm 1 to alloc a te tr a ffic among the
selected paths between a source-destination (S−D) pair.
We allocate traffic based on routing policy P(3) and
make sure all selected mLCP paths can jointly carry the
traff ic. The n, we desi gn the li nk layer multi-path re liable
routing scheme given byAlgorithm 2. This scheme en-
sures t he link layer re lia bility.
Based on a similar approach in [8], it can be proved
that, if Algor ithm 2 is used, t here are Nash equilibria for
all player nodes to truthfully declare their costs, and for-
warding packets according to the declared service relia-

Reliable Multi-path Routing in Selfish Networks with Hidden Information and Actions
33
bilities by all player nodes is a subgame perfect equili-
brium. Due to spac e limit, the p r oof is omitted in here .
4. Performance Evaluation
To establish m LCPs according to our criteria, any exist-
ing routing algorithm can be used. Here, we use the
commonly used Dynamic Source Routing (DSR) proto-
col as an example. The basic route discovery and route
maintenance are handled by DSR as usual. The only
modification is that instead of hop-count metric, the en-
crypted bidding cost and offered service reliability of
each node is included in the route request (RREQ) mes-
sage. Accordingly, the route reply (RREP) message sent
from destination to source includes the network graph
constructed from the information gathered in RREQ
message s. T hen the routing protocol determines f1,f2,...,fm
by usin g Algorithm 1.
In order to investigate the incentive aspect of our me-
chanism, we have developed an event-driven simulator
using C++ (Microsoft Visual Studio 2008, Ver.
9.0.21022.8 RTM) programming language. The general
settings of our simulation experiments are as follows.
There are 100 nodes and 250 links in the network. To
generate a network topology, these 100 nodes are ran-
domly connected by 250 links. The costs of links are
uniforml y chose n from [1, 5]. The reliability of a link or
a node is uniformly chosen from [0.001, 1]. For each
intermediate node, the cost involved in forwarding a
packet is dominated by the cost of the corresponding
outgoing links. Each source node splits traffic among all
but one of the available paths according to the specified
rules. Without loss of generality, the packet generation
rate at each source is assumed to be 1 packet per second,
and the transmission time of a packet between two nodes
is always 1 second.
4.1. Effects of Different Strategies
In this scenario, we investigate the effects of different
strategiesand we mainly look at two different aspects,
namely, the credit balance and the utility. The credit bal-
ance of each node is the payment received from other
nodes minus the payment made to others. The utility of
each node is the payment received from others minus the
cost involved in forwarding packets. There are two ac-
tions a node could choose to take during the auction,
namely honest and cheating. By honest, it means that a
node bids with its true cost and indeed provides its de-
clared service reliability, while cheating means a node
either understates or exaggerates its cost, and violate its
declared service reliability. Therefore there are totally
four combinations of different strategies depending on
actions by a node itself and other s. While we expec t that
when others behave honestly, the strategy of being hon-
est always leads to a better utility than the strategy of
cheating, we are also interested in comparing them with
the other two strategies experimentally. Therefore, we
generate the cheating scenario as follows. When we de-
cide a node to be cheating, with equal probability the
reported cost is either increased or decreased based on
Algorithm 2 Link layer multi-path reliab le routing
Suppose S wants to send data to D through mul-
tiple paths.
Input: we ighted graph G= {V, E, W} where |V|=n,
service cost of nodes, ci,i∈[1,n], service reliab ility of
nodes, γi,i ∈[1,n], link reliability, η(i, j), (i, j) ∈E;
Routing subgame:
1) Initialization: Sinitiates with bro adcasting a query
for forwarding packets with certain QoS. On re-
ceiving the query, each node player ideclares its ser-
vice cost , which may not be its tr ue cost,to provide
a forwarding service δ(i, j) on link (i, j) for each one
of its out-going neighbors j, and the corresponding
service reliabilityγi. For all links (i, j), we define its
weight ω(i, j) as /(γi· ηi, j);
2) Calculation: Scomputes all pathsto Dusing Di-
jkstra’s algorithm under each intermediate node’s
claimed cost with the corresponding service relia-
bility, and selects the first mLCP candidates;
3) Traffic allocation: Suses Algorithm 1to allocate
traffic among the selectedLCP candidates;
4) Forwarding subgame: When an intermediate
node ireceives a packet from its upstream node, it
will forward the packet to the next-hop node jusing
service reliability γior using some other forwarding
reliabilit y.
5) Compensation: Send s the tr ansmissi on, and only
if Dreceives the data correctly, Spays each inter-
mediate node iin one of the selected LCPs with
ε(C
k+1
) − ε(C
k
)+ ω(i
k
,j
k
).
Algorithm 1 Traffic alloca tion
Input: selected mpaths, cost of LCPi: ε(C1),...,ε(Cm);
Output: the fraction of data traffic f1, ..., fm;
do {
1) randomly generate f1, ..., fm, subject to
∑=
=
m
ii
f
11
,fi>0,i ∈[1,m],
2) sortfisuch thatf1>f2>··· >fm.
3)for i: 1 to m − 2
if[ε(Ci+1) − ε(Ci)]fi>[ε(Ci+2) − ε(Ci)]fi+1>[ε(Ci+2)
− ε(Ci+1)]fi+1,
flag = 1;
else
{flag = 0; break;}
}
while {flag == 0}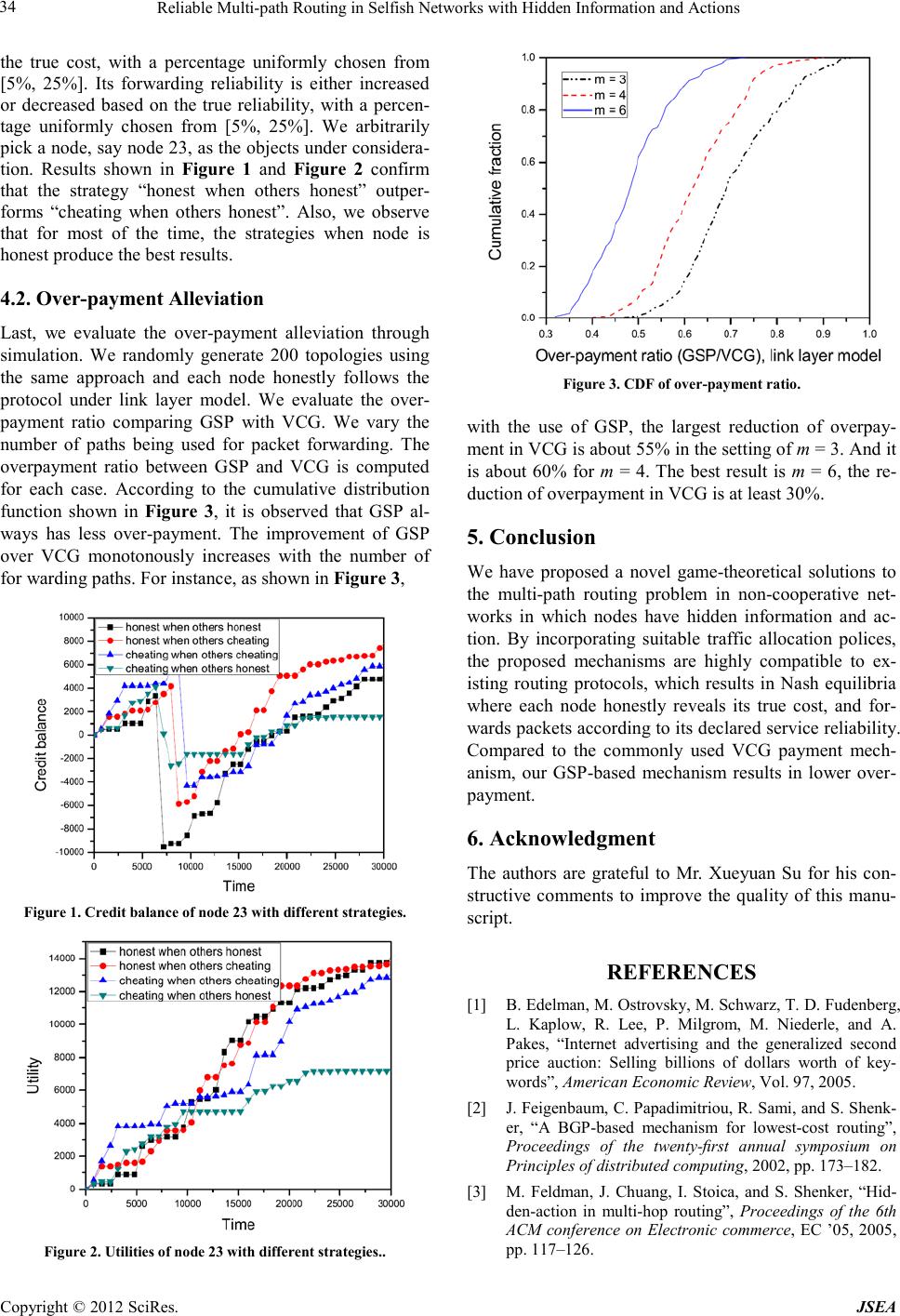

Reliable Multi-path Routing in Selfish Networks with Hidden Information and Actions
34
the true cost, with a percentage uniformly chosen from
[5%, 25%]. Its forwarding reliability is either increased
or decreased based on the true reliability, with a percen-
tage uniformly chosen from [5%, 25%]. We arbitrarily
pick a node, say node 23, as the objects under considera-
tion. Results shown in Figure 1 and Figure 2 confirm
that the strategy “honest when others honest” outper-
forms “cheating when others honest”. Also, we observe
that for most of the time, the strategies when node is
honest produce the best results.
4.2. Over-payment Alleviation
Last, we evaluate the over-payment alleviation through
simulation. We randomly generate 200 topologies using
the same approach and each node honestly follows the
protocol under link layer model. We evaluate the over-
payment ratio comparing GSP with VCG. We vary the
number of paths being used for packet forwarding. The
overpayment ratio between GSP and VCG is computed
for each case. According to the cumulative distribution
function shown in Figure 3, it is observed that GSP al-
ways has less over-payment. The improvement of GSP
over VCG monotonously increases with the number of
for ward ing p aths . For ins tance, as shown in Figure 3 ,
Figure 1. Credit balance of node 23 with different strategie s.
Figur e 2. Ut il it ies of node 23 with different strategies..
Figure 3. CDF of over-payment ratio.
with the use of GSP, the largest reduction of overpay-
ment in VCG is ab out 55 % in the sett in g of m = 3. And it
is about 60% for m = 4. The best result is m = 6, the re-
duction of overpayment in VC G is at le a st 30%.
5. Conclusion
We have proposed a novel game-theoretical solutions to
the multi-path routing problem in non-cooperative net-
works in which nodes have hidden information and ac-
tion. By incorporating suitable traffic allocation polices,
the proposed mechanisms are highly compatible to ex-
isting routing protocols, which results in Nash equilibria
where each node honestly reveals its true cost, and for-
wards packets according to its declared service reliability.
Compared to the commonly used VCG payment mech-
anism, our GSP-based mechanism results in lower over-
payment.
6. Acknowledgment
The authors are grateful to Mr. Xueyuan Su for his con-
structive comments to improve the quality of this manu-
script.
REFERENCES
[1] B. Ed elman, M. Ostrovsky, M. Schwarz, T. D. Fudenberg,
L. Kaplow, R. Lee, P. Milgrom, M. Niederle, and A.
Pakes, “Internet advertising and the generalized second
price auction: Selling billions of dollars worth of key-
words”, American Economic Review, Vol. 97, 2005.
[2] J. Feigenbaum, C. Papadimitriou, R. Sami, and S. Shenk-
er, “A BGP-based mechanism for lowest-cost routing”,
Proceedings of the twenty-first annual symposium on
Principles of distributed computing, 2002, pp. 173–182.
[3] M. Feldman, J. Chuang, I. Stoica, and S. Shenker, “Hid-
den-action in multi-hop routing”, Proceedings of the 6th
ACM conference on Electronic commerce, EC ’05, 2005,
pp. 117–126.

Reliable Multi-path Routing in Selfish Networks with Hidden Information and Actions
35
[4] D. Kar ger and E. Ni kolova, “On the expected VCG over-
payment in large networks”, Proceedings of45th IEEE
Conference on Decision and Control, December 2006, pp.
2831–2836.
[5] X.-Y. Li, Y. Wu, P. Xu, G. Chen, and M. Li, “Hidden
information and actions in multi-hop wireless ad hoc
networks”, Proceedings of the 9th ACM international
symposium on Mobile ad hoc networking and computing,
MobiHoc ’08, 2008, pp. 283–292.
[6] H. Liu and B. Krishnamachari, “A price-based reliable
routing game in wireless networks”, Proceedi ngs of the
2006 workshop on Game theory for communications and
networks, GameNets ’06, 2006.
[7] M. Osborne and A. Rubinstein, “A course in game
theory”, The MIT Press, 1994.
[8] X. Su, S. Chan, and G. Peng, “Auction in multi-pa th mu l-
ti-hop routing”, IEEE Communications Letters, Vol. 13,
No. 2, 2009, pp. 154–156.
[9] X. Su, S. Chan, and G. Peng, “Generalized second price
auction in multi-path routing with selfish nodes”, Pro-
ceedings of the IEEE GLOBECOM, 2009, pp.
3413–3418.
[10] K. Talwar, “The price of truth: Frugality in truthful me-
chani sms”, Proceedings of the 20th Annual Symposium
on Theoretical Aspects of Computer Science, 2003, pp.
608–619.
[11] H. R. Varian, “Position auctions”,International Journal of
Industrial Organization, Vol. 25, No. 6, 2007, pp.
1163–1178.
[12] W. Wan g, S. Eidenbenz, Y. Wang, and X.-Y. Li, “OURS:
optimal unicast routing systems in non-cooperative wire-
less networks”, Proceedings of the 12th annual interna-
tional conference on Mobile computing and networking,
MobiCom ’06, 2006, pp. 402–413.
[13] W. Wang and X.-Y. Li, “Low-cost routing in selfish and
ration al wirel ess ad ho c n etworks ”, IEEE Transactions on
Mobile Computing, Vol. 5, May 2006, pp. 596–607.
[14] W. Wang, X.-Y. Li, and X. Chu, “Nash equilibria and
dominant strategies in routing”, Proceed ings of the First
international conference on Internet and Network Eco-
nomics, WINE’05, 2005, pp. 979– 988.
[15] F. Wu, T. Chen, S. Zhong, L. E. Li, and Y. R. Yang, “In-
centive-compatible opportunistic routing for wireless
networks”, Proceedings of the 14th ACM international
conference on Mobile computing and networking, Mobi-
Com ’08, 2008, pp. 303–314.
[16] Y. Wu, S. Tang, P. Xu, and X.-Y. Li, “Dealing with sel-
fishness and moral hazard in non-cooperative wireless
networks”, IEEE Trans. on Mobile Computing, Vol. 9,
No. 3, March 2010, pp. 420–434.
[17] S. Zhong, J. Chen, and Y. Yang, “Sprite: a simple,
cheat-proof, credit-based system for mobile ad-hoc net-
wor k s ”, Pro ceedings of theINFOCOM 2003, 2003, pp.
1987–1997.
[18] S. Zhong, L. Li, Y. Liu, and Y. Yang, “On designing
incentive-compatible routing and forwarding protocols in
wireless ad-hoc networks: an integrated approach using
game theoretic and cryptographic techniques”, Wireless
Networks, Vol. 13, No. 6, 2007, pp. 799–816.