Engineering, 2012, 5, 88-93
doi:10.4236/eng.2012.410B023 Published Online October 2012 (http://www.SciRP.org/journal/eng)
Microchip Electrode Development for Traveling wave
Dielectrophoresis of Non-Spherical Cell Suspensi on s*
Sakshin Bunthawin1#, Jatuporn Kongklaew 1, Adisor n Tuantr anont2, Kata Jaruwongrangsri2, Thitima Maturos2
1Bi o tech nology o f Electromechan ics Res earc h Unit, Science of Physics, Faculty of Technology and Environment,
Prin ce of Songk la Universit y, Kathu, P huke t, 83120 Tha ilan d
2Nano-Electronic s and MEMs lab oratory, Na tiona l E lec tronic s and Computer T echn ology Center,
Pathumthani , 12120 Thai land
Received 2012
ABSTRACT
A microchip interdigitated electrode with a sequential signal generator has been developed for traveling wave dielectrophoresis
(twDEP ) of biological cell suspensi ons. The el ectrod e was fabricated on a microsco pe glass sli de and coated with a 0.5 μm thickness
of gold through a sputtering technique which was designed for large-scale inductions of cells rather than for individual cells as in
previous versions of our device. As designed for a representative cell size of 10 μm, the electrode array was 50 μm in width to allow
large nu mbers (>1 06) o f cells t o be p ro cessed . The seq u ent ial si gnal gener ato r pr odu ces an arbitr ary AC qu adrat ur e-ph ase to gen erate
travelin g electri c field for a microch ip interd igi tated elect rode. Each phase si gnal can b e au to matical ly alter ed an d alter nat ed with the
other phases within interval time of 0.01-30 seconds (controlled by programming). We demonstrate the system could be used to es-
timate the dielectric properties of the yeast Saccharomyces cerivisiae TISTR 5088, the green alga Tetraselmis sp. and human red
blood cells (HRBCs) through curve-fitting of dielectro- phor etic velociti es and critical frequencies.
Keywords: Traveling wave Dielectrophoresis; Microchip Interdigitated Electrode; Cell Suspensions; Dielectric Properties
1. Introduction
It is well known that a micro-interdigitated electrode can be
employed for dielectrophoresis (DEP) and traveling wave di-
electrophoresis (twDEP) of cell suspensions [1-4]. The micro-
electrodes for such work can generally be classified as three
types: a one planar linear interdigitated array [1,5-7], two pa-
rallel arra ys [2 -4 ,8, 9] and a mu lt i-co n cent ric ri ng st ructure [10] .
Such systems have considerable biotech- nological potential. It
is important to develop a user friendly version of the technolo-
gy that is able to be used routinely in a biotechnology laborato-
ry on a variety of types of cells.
The two-parallel electrode array might offer advantages for
both of cell manipulation and separation. The methods allow
cell suspensions to move either toward the electrode tips or
along the electrode track simultaneously, as a result of two
driving orthogonal forces [11]. Wang et al. [ 4] were the first to
term them the “unified force” for a dielectric sphere which
depends on both the real (Re[CMF]) and the imaginary part
(Im[CMF]) of the complex dielectric-frequency dependent
Clausius-Mossotti factor [CMF]. The model was then ex-
tended for a shelled spheroidal dielectric by [11]. These ana-
lyses describe cell behavior in a traveling electric field and the
models can be used to evaluate cell dielectric properties
through curve-fitting of experimentally measured dielectropho-
retic velo cities an d two critical frequencies.
The present study proposes a microchip interdigitated elec-
trode of two parallel arrays equipped with a sequential signal
generator for experiments on traveling wave dielectrophoresis
(twDEP) of cell suspensions. This microelectrode is designed
for large-scale inductions of cells rather than for individual
cells in our previous versions of the device such as “the
octa-pair interdigitated electrode” described by [11]. The se-
quen tial signal generato r generates traveli ng electric field o f an
arbitrary AC quadrature-phase to apply for t ype of cell. Dielec-
trophoresis and traveling wave dielectrophoresis spectra of a
non-spherical unicellular green alga, Tetraselmis sp ., yeast of
Saccharomyces cervisiate TISTR 5088 and human red blood
cells (HRBCs) wer e investigated. A curve-fitting method of cell
velocities and the lower critical frequency (LCF) were em-
ployed to determine their dielectric properties using a spheroid-
al cell model proposed in our previous work. Our newl y dev el-
oped system is a significant step towards biotechnology appli-
cations of the technology.
2. Theoretical Approaches
2.1. Traveling Dielectrophoretic Force
In AC electric field, the time-average dielectrophoretic force
(t F

) [4] actin g on a shel led sph eroidal diel ectric pos sessing th e
volume
2
4 /3ab π
(Figure 1) in a non-uniform sinusoidal
traveling electric field of magnitude
E
is given by [11]
( )
2
20222
Re[CMF] Im[CMF]
2
3
ts
xx yy zz
E
F abEEE π εεϕϕϕ
 ∇+
=
∇+∇+∇



(1)
where Re[CMF] and Im[CMF] are the real and the imaginary
*Facult y of Techn ology and En vironmen t and Prin ce of Songkla Un ive r
sity
are spon so r s f or the trip to BEB 2012.
#Corresponding author.

S. BUNTHAWIN ET AL.
89
parts of the complex dielectric- frequency dependent Clau-
sius-Mossotti factor [CMF],
0
ε
and
s
ε
are dielectric constants
of the vacuum and the suspending medium, resp ectively.
The value of
E
and its three components in the Cartesian
co-ordinate frame
,,xyz
(
,,
xyz
EEE
) is the root mean square
(rms) and
φ
is the electrical phase sequences addressing onto
each tip of the microelectrode (Figure 2). The real part of the
time-average dielectrophoretic force (
t
F

) represents the con-
ventional dielectrophoretic force (
cDEP
F

) and the imaginary
term is the traveling wave dielectrophoretic force (twDEP F

).
2.2. The Clausius-Mossotti Factor (CMF)
The Clausius-Mossotti factor (CMF) of a shelled spheroidal
model [11] possesses the physical parameters of the shell (cell
me mbr a ne) thickness ( δ ) and complex dielectric constants of
the shell (*
m
ε
), th e cytopl asm (*
c
ε
) and the suspending medium
(
*
s
ε
), respectively. As for the whole spheroid, the dielectric
properties can be considered as a single value of
*
eff
ε
, the so
called “t he effecti ve value of the complex relative permittivity”.
The [CMF] factor is defined as [ 12],
[CMF] ()
eff s
seffs k
L
εε
εεε
∗∗
∗∗∗
−
=+−
(2)
As is seen from (2) [11,13], both of Re[CMF] and Im[CMF]
are affected b y the d ielect ric an d con duct ivit y paramet ers o f the
cytoplasm (
,
cc
εσ
), the membrane (
,
mm
εσ
) and the suspending
medium (
,
ss
εσ
). The values of the parameters chosen were of
particular rel evance to cel ls.
2.3. Translational Ve locity and Two Crit ic al
Frequencies
Evaluation of cell translational velocity can be made using
Newton’s first laws of motion. For the present analysis, the
electric field gradient was assumed to be so low that the trans-
lational velocity of the spheroid will be essentially constant,
that is, the particle has reached terminal velocity, where the
translational force is balanced by the frictional drag force [11].
The translational speed of a spheroid for dielectrophoresis
(DEP) and traveling wave dielectro phoresi s (twDEP) are,
22
0
Re[] ,
9
s
DEP
bCMF E
vK
εε
η
∇
=′
(3)
22
0,,
Im[] ()
.
9
s ii
i xyz
twDEP
b CMFE
vK
εε ϕ
η
=
∇
=′
∑ (4)
where
η
is the viscosity of the suspending medium and
K′
is a shape factor. The direction of
cDEP
v
and
twDEP
v
depends
on the polarity of the Re[CMF] and Im[CMF], respectively.
Both velocit ies are written as a fu nction of cell diel ectric prop-
erties and they are frequency dependent. In case of the dielec-
trophoretic force, the spheroid experiences positive dielectro-
phoresis if the field frequency is in the range from the lower
critical frequency (
f
) to the higher critical value (
h
f
). The
higher critical frequency value is usually so high that it is not
measurabl e experi ment ally [11].
Figu re 1. Pro late-spheroidal cell geometry in three orthogonal axes.
Figure 2. Diagram of the electrode configuration in top view. The track length of the microchannel is about 750 μm and electric phase se-
quences (in radians ) are addressed to the tips of the electrode as the quadrature pattern.

S. BUNTHAWIN ET AL.
90
3. Experimental
3.1. Microelectrodes
The present version of the octa-pairs interdigitated gold elec-
trode was fabricated on microscope glass slides of dimension
75
×
25
×
1 mm (Marienfeld, Germany) (Figur e 2). The elec-
trode was strengthened by coating with a 0.5 μm thickness of
gold through a sputtering technique. Processes of photolitho-
graphy and wet-etching were employed to finalize a prototype
of the microelectrode. The electrode array was 50 μm in width
and the separation of the adjacent bars on the same array was
50 μm and the microchannel width between the two arrays was
50 μm. The microchannel track length was about 750 μm. The
glass slide of the microelectrode was mounted on the socket
base shown in (Figure 3). An inferometer was employed to
measure th e thickn ess of the elect r ode tip s .
3.2. Electrical Setup
The present version of the microchip interdigitated electrode
equipped with the sequential quadrature-signal generator was
developed from the previous version [11]. The sequential qua-
drature-signal generato r was the so urce gen erating t he traveling
electric field of a qu adrature ph ase for the 16 tips of the micro-
chip octa-pair interd igitated electrod e. The generator also h as a
function to split the electrical phase sequences (
φ
) i.e.
0,/ 2,,3/ 2 φπ ππ =
in series. They can be automatically
be altered and circulated to be in or out of phase within interval
times of 0.01-30 seconds (controlled by programming). The
equipment is connected directly to the microelectrode via the
computer cables and the microchip junction unit [11].
3.3. Cells Preparation
Yeast cells of Saccharomyces cerivisiae TISTR 5088 were
determined as a prolate spheroids of a = 4.0 ± 0.7 and b = 3.0 ±
0.4
μm
(mean
±
SD). They were cultured in Biotechnology of
Electromechanics research unit, Prince of Songkla University.
The cells were h arvested i n the station ary phase after 24 h r and
washed twice with deionized water, then centrifuged at 1,000
×
g for 2 min and re-suspended twice in 0.5 M sorbitol solution.
The solution conductivity
()
s
σ
was measured by using a
conductivity meter (Eutech Instruments, Cyberscan CON 11),
the conductivity was adjusted to be in the range of 3 to 300
mS.m-1 by adding 0.1M KCl solution, using a micropipette
(Nichipet, model 5000DG). For the experiments with dead
yeast cells, the cell suspension was heated to75C for 10 min
[8] and then cooled down to room temperature [8,14]. The sus-
pensi on was then centrifuged as described for viab le cells.
Phytoplankton of Tetraselmis sp., obtained from the National
Institute for Coastal Aquaculture (NICA), Songkla, Thailand.
The cells were cultured in Sato and Serikawa’s artificial sea-
water and harvested when the cells were in log-growth phase.
They were considered as a spheroid with average dimensions a
= 10.0 ± 0.7 µm and b = 8.0 ± 0.5 µm. Centrifugations at 7,000
rpm for 2 min were made to re-suspend twice in 0.5 M sorbitol
solution as described by [14]. The solution conductivity was
measured by using a conductivity meter (Tetracon 325, LF318 ),
and it was adjusted to be between 3 and 300 mS.m-1 by adding
0.1 M KCl solution, using a micropipette (Nichipet, model
5000DG). Non-viable cells were prep ared by boiling the cells at
80 °C for 10 min, cooling down to room temperature, centri-
fuging and re–suspending in the same experimental solution as
was used for the live cells [14]. Arsenic pre-treated cells were
prepared by adding arsenic solution (Sodium arsenite, NaAsO2,
MW 129.9) into the cell culture at concentrations varying from
1 to 150 ppm and leaving them for 24 hrs before being used in
an experi ment.
Human red b lood cells (HR BCs) were ob tained direct ly from
the blood bank of Vachira Phuket Hospital (Phuket, Thailand).
The normal mature red cells of blood group A and B were used
in the present study. Cell were centrifuged at 1,000 g for 2 min
then resuspended twice in isotonic sorbitol (300 mOsmol.kg-1).
The solution conductivity
()
s
σ
was adjusted to be between 3 to
300 mS.m-1 by adding 0.1M KCl solution. HRBCs were consi-
dered as an oblate spheroid with average radius dimensions a =
3.5 ± 0.3 µm, b = 3.0 ± 0.5 µm and c
≈
1.5 µm.
Figure 3. Microchip interdigitated electrode on the glass slide covered with PDMS sheet. The electrode has a fluid circulation system to flow
cell suspe nsions through the microchannel of the electro de using microtubes connected at the end of the track.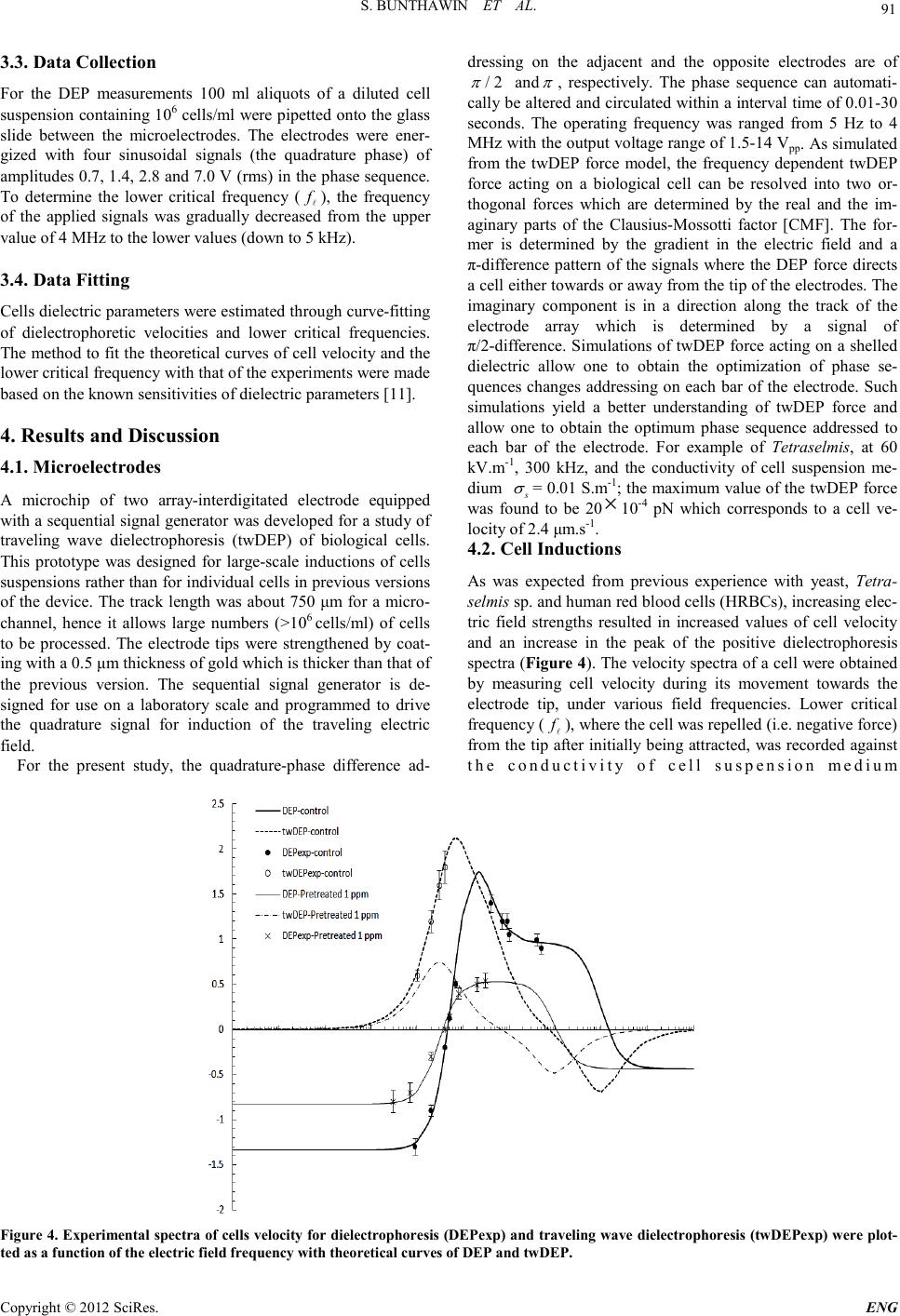

S. BUNTHAWIN ET AL.
91
3.3. Data Collectio n
For the DEP measurements 100 ml aliquots of a diluted cell
suspension containing 106 cells/ml were pipetted onto the glass
slide between the microelectrodes. The electrodes were ener-
gized with four sinusoidal signals (the quadrature phase) of
amplitudes 0.7, 1.4, 2.8 and 7.0 V (rms) in the phase sequence.
To determine the lower critical frequency (
f

), the frequency
of the applied signals was gradually decreased from the upper
value of 4 MHz to the lower values (down to 5 kHz).
3.4. Data Fitting
Cells d ielect ric p ara meters wer e e stimat ed t hr ou gh curve-fitting
of dielectrophoretic velocities and lower critical frequencies.
The metho d to fit th e theoretical curves of cell velocity and the
lower critical frequency with that of the experiments were made
based on the known sensitivities of dielectric parameters [11].
4. Results and Discussion
4.1. Microelectrodes
A microchip of two array-interdigitated electrode equipped
with a sequent ial signal gen erator was developed for a stud y of
traveling wave dielectrophoresis (twDEP) of biological cells.
This prototype was designed for large-scale inductions of cells
suspensions rather than for individual cells in previous versions
of the device. The track length was about 750 μm for a micro-
channel, hence it allows large numbers (>106 cells/ml) of cells
to be processed. The electrode tips were strengthened by coat-
ing with a 0.5 μm thickness of gold which is thicker than that of
the previous version. The sequential signal generator is de-
signed for use on a laboratory scale and programmed to drive
the quadrature signal for induction of the traveling electric
field.
For the present study, the quadrature-phase difference ad-
dressing on the adjacent and the opposite electrodes are of
/2 π and
π
, respectively. The phase sequence can automati-
cally be alt ered and ci rculated wit hin a interval time of 0.01-30
seconds. The operating frequency was ranged from 5 Hz to 4
MHz with the output voltage range o f 1.5-14 Vpp. As simulated
fro m the twDEP force model, the frequency dependent twDEP
force acting on a biological cell can be resolved into two or-
thogonal forces which are determined by the real and the im-
aginary parts of the Clausius-Mossotti factor [CMF]. The for-
mer is determined by the gradient in the electric field and a
π-difference pattern of the signals where the DEP force directs
a cell eith er towards o r away from the tip of the electr odes. The
imaginary component is in a direction along the track of the
electrode array which is determined by a signal of
π/2-difference. Simulations of twDE P force acting o n a shelled
dielectric allow one to obtain the optimization of phase se-
quences changes addressing on each bar of the electrode. Such
si mul ations yield a better understanding of twDEP force and
allow one to obtain the optimum phase sequence addressed to
each bar of the electrode. For example of Tetraselmis, at 60
kV. m-1, 300 kHz, and the conductivity of cell suspension me-
dium
s
σ
= 0.0 1 S.m-1; the maximum valu e of the twDEP force
was found to be 20
×
10-4 pN which corresponds to a cell ve-
locity of 2.4 μm.s-1.
4.2. Cell Inductions
As was expected from previous experience with yeast, Tetra-
selmis sp. and human red blood cells (HRBCs), increasing elec-
tric field strengths resulted in increased values of cell velocity
and an increase in the peak of the positive dielectrophoresis
spectra (Figure 4). The velo city spectra of a cell were obtained
by measuring cell velocity during its movement towards the
electrode tip, under various field frequencies. Lower critical
frequency (
f

), wh e re th e cell was repel led (i.e. negative force)
from the tip after initially being attracted, was recorded against
the conductivity of cell suspension medium
Fig ure 4. Experi mental spec tra of cell s veloc ity fo r diel ectro phores is (DEP exp) a nd tra veli ng wave dielectrophoresis (twDEPexp) were plot-
ted as a function of the electric field frequency with theoretical curves of DEP and twDEP.

S. BUNTHAWIN ET AL.
92
(
s
σ
). It was observed that as the
s
σ
was increased the
f
was
shifted towards a higher frequency value for S. cerevisiae
TISTR 5088, Tetraselmis sp. and HRBC. It should be noted
that cell velocity spectra for all three cell types were reduced
significan tly at greater
s
σ
values. According to the model, when
the increased
s
σ
reached a critical value the attractive force
became negligible, implying an equivalence to the cytoplasmic
conductivity. Yeast cells at a cell density of 105 ml-1 displayed
positive dielectroph oretic force over a frequ ency range b etween
50 kHz and 15 MHz, when increasing
s
σ
from 0.01 to 0.25
S.m-1. For traveling wave dielectrophoresis, the cells expe-
rienced the traveling wave dielectrophoretic force at about 60
kHz and
s
σ
of 0.01-0.25 S.m-1 for electric field strength of
10-143 kV/m. By curve-fitting methods to the model, it was
shown t hat dielectric valu es of yeast were similar to what were
reported using other methods [11,15,16]. The cytoplasmic and
the membrane conductivity for yeast cells were 0.23 S.m-1 and
0.1 µS.m-1, respectively. For Tetraselmis sp., cells experienced
posi tive d iel ectrop horesi s o ver a frequency ranged from 50 kHz
and 0.5 MHz, when increasing
s
σ
from 0.01 to 0.10 S.m-1.
Tetraselmis sp . experien ced traveling wave dielectrophoresis in
the 20 -48 kHz frequ ency range wit h
s
σ
of 0.01-0.37 S.m-1 for
28-143 kV/m. In the case of HRBC, it was found that positive
dielect rophoresis occurred in the range 8 kHz-10 MHz, when
increasing
s
σ
from 0.64 to 60 mS.m-1. HRBC cells expe-
rienced traveling wave dielectrophoresis in the 50-150 kHz
frequency range with
s
σ
of 56 S.m-1 and 4.7-14 kV/m for
both type of A and B groups.
Dead yeast cells exhibited positive dielectrophoresis over the
frequency range from 100 kHz (
f
) to 1 MHz if the medium
conductivities were between 0.01-0.04 S.m-1. The value
of
f

was shifted towards greater values when
s
σ
was increased.
The spectra o f cells t ranslat ion al velocit y and criti cal frequen cy
of the living and dead cells were different and allowed the dif-
ferent dielectric properties of these to be determined. The DEP
velocity (
cDEP
v

) spectra and the value of
f
of Tetraselmis sp.
were investigated in control and arsenic treated cells. Increasing
arsenic level from 1 to 150 ppm reduced the magnitude of cell
velocity and shifts the
f
to a lower value. When the control and
the arsenic contaminated cells were combined, one can distin-
guish the control from the arsenic pretreated cells if the fre-
quency used was below 35 kHz.
The s pecific capacit ance (
m
C
) and conductance (m G) of the
membrane were calculat ed for co ntrol and arsenic treat ed cells.
The results showed that
m
C
and
m
G
of living and dead yeast
cells were 1 0.1 mF.m-2, 8.3 S.m-2 and 18.4 mF.m-2, 33.3
3
10×
S.m-2, respectively. Thus arsenic has a relatively small effect
on
m
C
but a ver y large effect o n
m
G
in yeast. The values of m C
and m
G
of the control Tetraselmis sp. cells were 5.5 mF.m-2
and 13.0 S.m-2, respectively, which were smaller than that of
the arsenic pretreated cells. For 1, 5, 10, 50, and 150 ppm pre-
treated cells, m Cvalues were 6.7, 8.3, 10.8, 14.3 and 21.8
(mF .m-2), respectively. It was interesting that while the
m
Cval-
ues of the arsenic pretreated cells were increased, the value
of
m
G
remained constant and the conductivity of cell membrane
(
m
σ ) was 23.0 S.m-2.
5. Acknowledgements
This work has been supported by National Electronics and
Computer Technology Center, National Science and Technol-
ogy Development Agency (NSTDA), Thailand (grant
NT-FD-B-22-EDS-19-54-05). Thanks are also extended to
Vachira Phuket Hospital (Phuket, Thailand) and NICA for pro-
viding HRBCs and Tetraselmis sp. cells, respectively, and Dr.
Raymond Ritchie for help with the manuscript.
REFERENCES
[1] S. Masuda, M. Washizu, and I. Kawabata, “Movement of blood
cells by nonuniform traveling field,” IEEE Trans. Ind. Applicat.,
vol. 24, pp. 214-222, 1988.
[2] G. Fu h r, R . Ha ged orn , T. Mu ller, W. Ben ec k e, B. Wagn er , an d J.
Gimsa, “Asynchronous traveling wave induced linear motion of
living cells, ” Journal of Studia Biophisica, vol. 140 (2),
pp.79-102. 1991.
[3] R. Hagedorn, G. Fuhr, T. Muller, and J. Gimsa, “Traveling wave
dielectrophoresis of microparticles,” Electrophoresis, vol.13,
pp.49-54, 1992.
[4] X. B.Wang, M. P. Hughes, Y. Huang, F. F. Becker, and P. R. C.
Gascoyne, “Non-uniform spatial distributions of both the mag-
nit ude an d ph ase of AC elect ric fi elds d eter min e dielec tr oph oret-
ic forces,” Biochimica et Biophysica Acta., vol. 1243,
pp.185-194, 1995.
[5] M. P. Hughes, “AC electrokinetic: applications for nanotechnol-
ogy,” Na notechnology, vol. 11, pp.124-132, 2000.
[6] T. B. Jones, “Basic theory of dielectrophoresis and electrorota-
tion,” IEEE Engineering in Medicine and Biology Magazine,
vol. 22(6), pp. 33-42, 2003.
[7] R. Pethig, M. S. Talary, and R. S. Lee, “Enhancing travel-
ing-wave dielectroph oresis with si gnal superposi tion,” IEEE En-
gineering in Medicine and Biology Magazine, vol. 22(6), pp.
43-50, 2003.
[8] M. S.Talary, J. P. H. Burt, J. A. Tame, and R. J. Pethig, “Elec-
tromanipulation and separation of cells using traveling electric
fields,” Journal of Physics D: Applied Physics. Vol. 29, pp.
2198-2203, 1996.
[9] L. M. Fu, G.B. Lee, Y. H. Lin, and R. J. Yang, “Manipulation of
microparticles using new modes of traveling wave dielectropho-
retic force: Numerical simulation and experiments,” Journal of
IEEE/ASME Transactions (Mechatronics), vol. 9 (2), pp.377-383.
2004.
[10] E. G. Cen, C. Dalton, Y. Li, S. Adamia, L.M. Pilarski, and
K.V.I.S. Kaler, “A combined dielectrophoresis, traveling wave
dielect rop h oresis and elect rorota t ion m ic rochip for th e m anipu la-
tion and characterization of human malignant cells,” Journal of
MicrobiologicalMethods, vol.58, pp.387-401, 2004.
[11] S. Bunthawin, P.Wanichapichart, A.Tuantranont, and H. G. L.
Coster, “Dielectrophoretic spectra of translational velocity and
critical frequency for a spheroid in traveling electric field,” Bio-
microfluidics. 4:014102 [doi:10.1063/1.3294082], 2010.
[12] L. D. Land au and E. M. Lift sc hit z, Elekt rodan ami k der k ontinua.
Akadem ie Verlag, Berlin, 1985 .
[13] K. Asami, “Characterization of biological cells by dielectric
spectroscopy,”Non-Crystal Solids, vol. 305, pp . 268-277, 2002.
[14] P. Wanichapichart, T. Wongluksanapan, and L. Khooburat,
“Electrorotation: diagnostic tool for abnormality of marine phy-
toplankton cells,” Proceedings of the 2nd IEEE International
Conference on Nano/Micro Engineering and Molecular Systems,

S. BUNTHAWIN ET AL.
93
Bangkok, Thailand, January 16 - 19, pp.1115-1120, 2007.
[15] X. F. Zh ou, G. H. Markx, and R. Pethi g, “Effect of biocide c on-
centration on electrorotation spectra of yeast cells,” Biochim.
Biophys. Acta., vol.1281, pp. 60-64, 1996.
[16] S. Bunth awi n, P.Wa nich api chart , and J. Gims a, “An in vest igation
of dielectric properties of biological cells using RC-model,”
Songklanakarin Journal of Science and Technology, vol.29 (4),
pp.1163-1181, 2007.