Advances in Ma terials Physics and Che mist ry, 2012, 2, 248-252
doi:10.4236/ampc.2012.24B063 Published Online December 2012 (htt p://www.SciRP.org/journal/ampc)
Resolving a Challenge i n t he Modeling of Hydrogen
Production Using Steam Reforming of Methane in Monolith
React ors Using CFD Methods
Mohammad Irani
Research Institute of Petroleum Industry (RIPI), Tehran, Iran
Received 2012
ABSTRACT
Reaction modeling of SMR (Steam Methane Reforming) process inside monolith reactors using two approaches were investigated
and compared with each other . In the first ap proach, the reaction s were assu med to take p lace exactly on the wall su rfaces, while in
the seco nd approach th ey considered in side a thin thickness n ear the walls. Experi ments of SMR were carried o ut in a lab-scale mo-
nolith reactor. A single-channel was considered and CFD model were developed for each of aforementioned approaches. Compari-
sons b etween model ing resu lts an d experi mental d ata sho wed that t he first appr oach (su rface model) give s better result s. P erforming
reaction s are d if ficul t an d exp ensi ve, CF D si mulat io ns ar e con sid ered as n umeric al e xper imen ts in man y cases. It was co ncluded that
obtained results from CFD analysis gives precise guidelines for further studies on optimization of SMR monolithic reactor perfor-
mance.
Keywords: Hydrogen Production; Monolith ic Reactor; CFD; SMR; Surface-model; Volume-model
1. Introduction
Hydrogen is one o f the cl eanest fuels whi ch can b e used inst ead
of fossil fuels. There are variety of applications for hydrogen in
industries such as: fuel cells, green cars, metal production and
fabrication, Petroleum recovery and refinery, chemical processing,
power generation, etc. The mentioned applications made the
Hydrogen a strategic product. The most famous process for
hydrogen production is Steam Reforming of Methane (SMR)
which converts Methane and other hydrocarbons presented in
natural gas into Hydrogen in large centralized industrial plants.
Researchers are being done in order to develop small-scale
SMR technologies to enable the development of distributed
hydrogen production and delivery infrastructure [1,2]. There-
fore due to attaining this goal small-scale SMR technologies
should be modeled and optimized [3-7]. Monolith catalysts can
be widely used in many applications particularly for their high
geometric su rface are a, low pr essure d rop and good mechan ical
strength and durability [8]. In addition using monolithic
reactors have significant advantages such as reduced capital
cost, smaller footprints and potentially easier transportation [1,
9-11]. These advantages can be particularly valuable when
considering the exploration of remote resources such as offshore
reserves of natural gas[12]. In the present work, hydrogen
production in a bench-scale SMR monol ith reacto r was stud ied.
Two different approaches were presented in the literature for
implementing reaction rat es in monolith react or models , namely
surface approach and volumetric approach. In the first approach,
the diffusion into the thin catalytic layers (washcoat) in
modeling of monolithic reactors is neglected and the reactions
are assumed to take place at the surface of the washcoat. Case
studies for this approach include steam Methane reforming
(SMR) [14], steam reforming of methanol [15-17], ethanol steam
reforming [18] and autothermal reforming of n-hexadecane [19].
Hartmann et al. [20,21] studied Hydrogen production by
catalytic p artial o xidation of iso-octane at varying flow rate an d
fuel/oxygen ratio.
Massing et al. [24] studied the catalytic conversion of
propene and demonstrated that diffusional limitations within
the washcoat limit the propene conversion. Stutz and
Poulikakos [25] considered diffusion and reaction inside the
washcoat of a monolithic reformer.
In the present study, the surface and volumetric approaches
were used to model SMR in a single-channel monolith reactor.
The obtained results from each model were compared with
experimental dat a.
2. Mathematical Model
In order to model the problem, five sets of equations should be
solved; continuity equation, momentum balance, energy and
species transport equations.
.() 0v ρ
∇=
(1)
( )
.( ).
T
vvPvvg S ρ µρ

∇=−∇+∇∇ +∇++

(2)
()( )
1
.()..
n
ii R
i
vH PhJqS ρ
=

∇++ ∇=−∇+


∑ (3)
where,
ρ
represents mi xture den sity, v is veloci ty vector,
µ
is the mixture viscosity, H and hi are total enthalpy and
enth alpy of species, respecti vely and Ci stands for concentration
of chemical sp ecies . P i s the static pr essur e and SR is the heat of
reaction.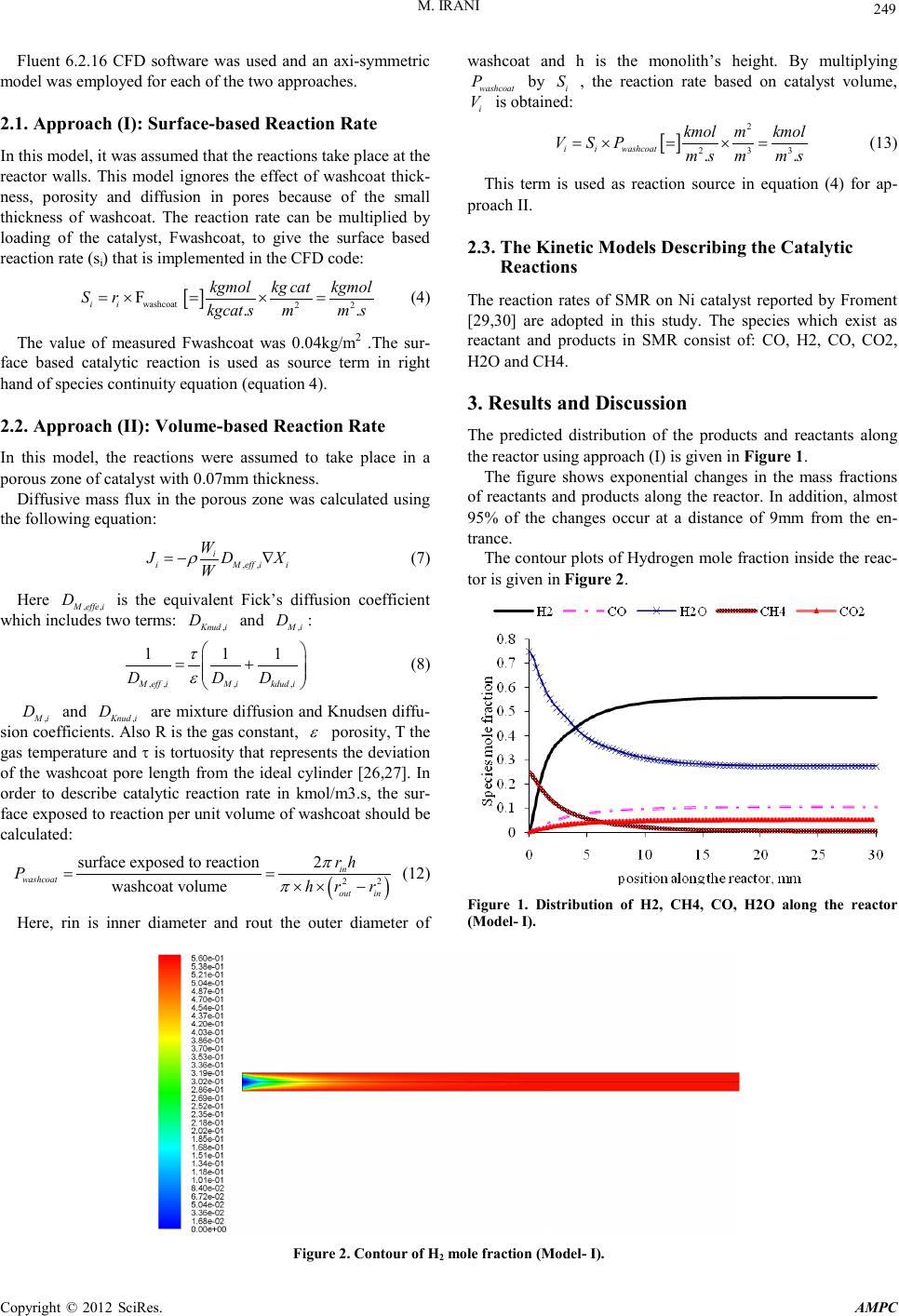

M. IRANI
249
Fluent 6.2.16 CFD software was used and an axi-symmetric
model was employed for each of the two approaches.
2.1. Approach (I): Surfa c e-based Reaction Rate
In this model, it was assumed that the reacti ons t ake place at the
reactor walls. This model ignores the effect of washcoat thick-
ness, porosity and diffusion in pores because of the small
thickness of washcoat. The reaction rate can be multiplied by
loading of the catalyst, Fwashcoat, to give the surface based
reaction rate (si) that is implemented in the CFD code:
[ ]
washcoat 22
F..
ii
kgmolkg catkgmol
Sr kgcat smms =× =×=
(4)
The value of measured Fwashcoat was 0.04kg/m2 .The sur-
face based catalytic reaction is used as source term in right
hand of species continuity equation (equation 4).
2.2. Approach (II) : Volume-based Reaction Rate
In this model, the reactions were assumed to take place in a
porous zone of catalyst with 0.07mm thickness.
Diffusive mass flux in the porous zone was calculated using
the following equation:
,,
i
iM eff ii
W
J DX
W
ρ
=−∇
(7)
Here
,,
Meffe i
D is the equivalent Fick’s diffusion coefficient
which includes two terms:
,Knud i
D
and
,Mi
D
:
,,, ,
1 11
M effiM ikdud i
D DD
τ
ε

= +



(8)
,Mi
D
and ,Knud i D are mixture diffusion and Knudsen diffu-
sion coefficients. Also R is the gas constant,
ε
porosity, T the
gas temperatu re and τ is tortuosity that represents the deviation
of the washcoat pore length from the ideal cylinder [26,27]. In
order to describe catalytic reaction rate in kmol/m3.s, the sur-
face exposed to reaction per unit volume of washcoat should be
calculat ed:
( )
22
surface exposed to reaction2
washcoat volumein
washcoat
out in
rh
Phr r
π
π
== ×× −
(12)
Here, rin is inner diameter and rout the outer diameter of
washcoat and h is the monolith’s height. By multiplying
washcoat
P
by
i
S
, the reaction rate based on catalyst volume,
i
V
is obtained:
[ ]
2
2 33
..
ii washcoat
kmol mkmol
VSP ms mms =×=×=
(13)
This term is used as reaction source in equation (4) for ap-
proach II.
2.3. The Kinetic Models Describing the Catalytic
Reactions
The reaction rates of SMR on Ni catalyst reported by Froment
[29,30] are adopted in this study. The species which exist as
reactant and products in SMR consist of: CO, H2, CO, CO2,
H2O and CH4.
3. Results and Discussion
The predicted distribution of the products and reactants along
the reactor usin g approach (I) is given in Figure 1.
The figure shows exponential changes in the mass fractions
of reactants and products along the reactor. In addition, almost
95% of the changes occur at a distance of 9mm from the en-
trance.
The contour plots of Hydrogen mole fractio n inside the reac-
tor is given in Figure 2 .
Figure 1. Distribution of H2, CH4, CO, H2O along the reactor
(Model- I).
Figure 2. Contour of H2 mole fr ac tion (Mo del- I).

M. IRANI
250
Higher concentrations of Hydrogen are observed near the
reactor walls wher e it is produ ced. Ho wever, the rad ial gradien t
of hydrogen concentration is descended along the reactor due to
convectional and diffusional mass transfer and lower rate of
Hydrogen production in the frontier regions. Figures 3 and 4
reveal that the main changes in the concentrations of reactants
and products occur in the first 9mm of the reactor. The pre-
dicted distribution of the products and reactants along the reac-
tor using approach (II) is given in Figure 8.
This figure shows that there are considerable changes in the
concentrations at the reactor output. Radial distribution of
hydrogen plotted in Figure 9 confirms this point by showing
that there is still a significant difference between the
concentrations in the lengths of 25 and 30mm. The product gas
species from experi ment s were measured by GC. A compariso n
between experimental and predicted values of Methane
conversion at different reactor temperatures is given in Figure
6 . This figure shows that the predicted conversions of approach
(I) at all the examined temperatu res are more accurat e than that
of approach (II).
It can be explained by the fact that due to low diffusion coef-
ficient in the washco at, the sp ecies can o nly diffuse to a limited
thickness of the washcoat. Therefore, the available volume of
the porous zone for chemical reactions is smaller than the total
volume of washcoat. Thus the conversions of the reactions are
underestimated in this model. In the other hand, by considering
the fact th at the resid ence time of gas species in side the reacto r
is in the order of milliseconds [10], it can be realized that the
species don't have enough opportunity to diffuse into the porous
Figure 3. H2 m ole fraction at 6 locat ion s (Mode l- I).
Figure 4. ِ◌Distribution of H2, CH4, CO, H2O along the reactor
(Model- II).
washcoat.
The comparison of predicted and experimental values of
Hydrogen yield (Figure 7) shows similar results and the
predictions of approach (I) are better than that of approach (II)
for all exa min ed reacto r temperatures .
The experi mental an d p redicted values of Hydrogen selectiv-
ity are compared in Table 1. The values in this table show that
the error values for approach (I) are less than 5%, while for
approach (II) it is more than 30%. The whole above discussion
testify that predictions of approach (I) is more accurate than
that of approach (II).
Figure 5. H2 m ole fraction at 6 locat ion s (Mode l- I).
65
70
75
80
85
90
95
100
9239731023 10731123
Temperature(K)
% CH4 Co nversion
Experiment Model - I Model - II
Figure 6. Comparison of CH4 conversions between Model-1, Mod-
el-2 and experiments.
Figure 7. Comparison of H2 yield between Model-I, Model-II and
experiments.

M. IRANI
251
Table 1. Comparisons between the two models and experimental
results.
Model 1 Model 2 Exp Model 1
Error (%) Model 2 Error (%)
H2 selectivity*
(T=700 ºC) 71.26 51.83 73.78 3 .41 2 9 .7
H2 selectivity
(T=750 ºC) 75.65 55.37 77.81 2.775 2 8.8
H2 selecti vity
(T=800 ºC) 7 8 .1 58.36 79.11 1 .27 2 6 .2
4. Conclusion
The current study presents two approaches for numerical mod-
eling and implementation of reaction rates in simulation of heat
and mass transfer in monolithic reactors. The chemical conver-
sion on the Ni-catalyst is modeled using general kinet ic models
for SMR and Water–Gas-Shift (WGS) reaction rates based on
Langmuir–Hinshelwood type. Monolithic reactor was simu-
lated using mentioned two approaches under steady-state con-
dition. The results of two approaches were compared to cor-
responding experimental data and a comprehensive evaluation
was carried out. The results showed that the predictions of sur-
fac e-based approach are more accurate than that of vo-
lume-based approach. The volume-based mod el underest imates
the conversion of reactions. Small values of effective diffusion
coefficien t in po rous washcoat layer and low resid ence ti me are
the main reasons of discrepancy between volume-based ap-
proach and experiment results. In total, despite of its ease of
implementation, the first approach (surface reactions) gives
better r esults both in generality and accuracy. Also. It was con-
cluded that obtained results from CFD analysis gives precise
guidelines for further studies on optimization of SMR mono-
lithic reactor performance.
REFERENCES
[1] A.Y. Tonkovich , S. Perry, Y. Wang, D. Qiu, T. LaPlante and
W.A. Rogers , “Microchanel process technology for compact
Methane steam reforming,” Chem. Eng .Sci , vol. 59, pp.
4819–48 24, 2004.
[2] D. Hickman and L.D. Schmidt, “ Production of syngas by
direct catalytic oxidation of Methane”, Science , vol. 259, pp.
343–346,1993.
[3] E.E. Gonzo, “ Hydrogen from methanol-steam reforming.
Isothermal and adiabatic monolith reactors’ simulation.” ,Int J
Hydrogen Energy, vol.33,pp. 3511 – 3516, 2008.
[4] E. Lo´pez, A. Irigoyen, T. Trifonov, A. Rodrı´guez, J. Llorca,
“ A million-cha nnel reformer on a fin gertip: Moving d own the
scale in hydrogen production”, Int.J. Hydrogen Energy,
vol.35 ,pp. 3472 – 3479, 2010.
[5] L. Shi, “ Bayless D J and Prud ich M E. A CFD model of auto-
therma l reformi n g”, Int J Hydrogen E n ergy ,vol .35 ,pp . 3472 –
3479 , 201 0.
[6] W. Cai, F. Wang, A.V. Veen, C. Descorme, Y. Schuurman and
W. Shen , “ Mirodatos C. Hydrogen production from ethanol
steam reforming in a micro-channel reactor”, Int J Hydrogen
Energy, vol. 35,pp. 1152 – 1159, 2010.
[7] X. Zhai, S. Ding, Y. Cheng, Y. Jin and Y. Cheng, “ CFD si-
mulation with detailed chemistry of steam reforming of Methane
for hydrogen production in an integrated micro-reactor” , Int J
Hydrogen Energy , vol. 35, pp. 5383 – 5392, 2010.
[8] T. Boger, “ Monolithic catalysts for the chemical Industry”, Ind
Eng Ch em Res, vol.43 ,pp. 4602-4611, 2004.
[9] R.S. Benson and J .W. Ponton., “ Process Miniaturisation-A
Route to Total Environmental Acceptability”, Chem. Eng. Res.
Des. ,vol. 71,pp . 160–168,1993.
[10] A.Y. Tonkovich, B. Yang , S.T. Perry, S.P. Fitzgerald, Y. Wang ,
“ From seconds to milliseconds to microseconds through tai-
lored mic rocha nn el rea ct or d esi gn of a stea m Met h aner efor m er” ,
Catal Today , vol.120 ,pp. 21-29, 2007.
[11] R. J. Bradley, L.C. Nathan, N.T. Diana, A.D. Robert, D.H.
Jamelyn, Y. Wang , “ Engineered SMR catalysts based on hy-
drothermally stable, porous, ceramic supports for microchannel
reactors” ,Catal Today,vol. 120 , pp. 54-62, 2007.
[12] A.K. Avci, D.L. Trimm, M. Karakaya, “ Microreactor catalytic
combustion for chemicals processing”, Catal Today,vol.155 ,pp.
66-74 ,2010.
[13] G. Arzamendi, P.M. Diéguez, M. Montes, J.A. Odriozola,
E. Falabella, E. Sousa-Aguiar and L.M .Gandía, “Methane
steam reforming in a microchannel reactor for GTL intensifica-
tion: A computational fluid dynamics simulation study ”, Chem-
ica l Engineering Journa l , vol.168 ,pp. 168-173, 2009.
[14] A. Fazeli, M. Behnam, “ Hydrogen production in a zigzag
and straight catalytic wall coated micro channel reactor by CFD
modeling”, Int J Hydrogen Energy, vol.35 ,pp. 9496-9503,
2009..
[15] G. Arzamendi, P.M. Diéguez, M. Montes, M.A . Centeno, J.A.
Odriozola, L.M . Gandía, “In tegration of methanol steam re-
forming and combustion in a microchannel reactor for H2 pro-
ducti on: A CF D sim ulati on s tudy ”, Catalysis Today, vol.143,
pp. 25-31,2009.
[16] S. Fukahori, H. Koga, T . Kitaoka, M. Nakamura, H. Wa-
riis hi , “ Steam reforming behavior of methanol using pa-
per-structured catalysts: experimental and computational fluid
dynamic analysis”, Int J Hydrogen Energy, vol. 33, pp.
1661-70¸2008.
[17] I.Uriz, G.Arzamendi, E.,López,J. Llorca, L.M. Gandía , “Com-
putational fluid dynamics simulation of etha nol steam reformi ng
in catalytic wall microchannels ”, Chemical Engineering Jour-
nal, vol.167 ,pp. 536-544 ,2011.
[18] L. Shi, D.J. Bayless and M.E. Prudich , “ A CFD model of
autothermal reforming” , Int J Hydrogen Energy, vol.34 ,pp.
7666-7675, 2009.
[19] M. Hartmanna, L . Maierb, O. Deutschmann, “ Hydrogen
produc tion by catalytic partial oxidation of iso-octan e at varyin g
flow rate and fuel/oxygen ratio: From detailed kinetics to reactor
behavior”, Applied CatalysisA:General , vol.391, pp. 144–152,
2011.
[20] M . Hartmann, L. Maier and H.D .Minh, “ Deutschmann O.
Catalytic partial oxidation of iso-octane over rhodium catalysts:
An experimental, modeling, and simulation study”, Combustion
and Flame , vol.157 , pp. 1771–1782,2010.
[21] K. Zygourakis and R. Aris, “ Multiple oxidation reactions and
diffusion in the catalytic layer of monolith reactors”, Chem. Eng
Sci ,vol.32, pp. 733-744 ,1983.
[22] Influence of the propene diffusion inside the catalytic layer”,
Chemical Engineering Sc ience, vol. 55,p p. 1707-1716,2000.
[23] M.J. Stutz, D. Poulikakos, “ Optimum washcoat thickness of a
monolith reactor for syngas production by partial oxidation of
Methane” ,Chemical Engineering Science ,vol.63 ,pp. 1761 –
1770,2008.
[24] N. Mladenov, J. Koop, S. Tischer, O. Deutschmann “Modeling
of transport and chemistry in channel flows of automotive cata-
lytic converters ”, Chem.Eng.Sci, v ol.65, pp. 812-826, 2010.

M. IRANI
252
[25] Hoseini N, Msc thesis, Tarbiat Modares University: Tehr an- Iran,
2010.
[26] J.P. Du Plessis, W.G. Gray, “ Pore-scale modeling of interstitial
transport phenomena. In: Fluid Transport in Porous media”,
Computational Mechanics Publication Southampton, pp.
61–104,1997.
[27] H.K. Plummer, R.J. Jr, R.H. Baird, A.A. Hammerle and Adamc-
zyk JD, “Measurement of Automotive Catalyst Washcoat Load-
ing Parameters by Microscopy Techniques”, Microscopy and
Microanalysis, vol.5 , pp. 267-281,1999.