Paper Menu >>
Journal Menu >>
 Journal of Software Engineering and Applications, 20 12, 5, 14-19 doi:10.4236/jsea.2012.512b003 Published Online December 2012 (http://www.SciRP.org/journal/jsea) Copyright © 2012 SciRes. JSEA Maximum Load Balancing with Optimized Link Metrics Touraj Shabanian, Massoud Reza Hashemi, Ahmad Askarian Department of Electrical and Computer Engineering, Isfahan University of Technology, Isfahan, Iran. Email: shabanian@ec.iut.ac.ir, hashemim@cc.iut.ac.ir, a.askarian@ec.iut.ac.ir Received 2012 ABSTRACT Traffic engineering helps to use network resources more efficiently. Network operators use TE to obtain different ob- jectives such as load balancing, congestion avoidance and average delay reduction. Plane IP routing protocols such as OSPF, a popular intradomain routing protocol, are believed to be insufficient for TE. OSPF is based on the shortest path algorithm in which link weights are usually static value without considering network load. They can be set using the inverse proportional bandwidth capacity or certain value. However, Optimization theory helps network researchers and operators to analyze the network behavior more precisely. It is not a practical approach can be implemented in tradi- tional protocol .This paper proposes that to address the feasibility requirements, a weight set can be extracted from op- timization pr oblem use as a link metric in OSPF. W e show the routes t hat selected i n OSPF with these metric distrib ute the traffic more c lose to optimal situation than ro utes from OSPF with defa ult metric. Keywords: Component; Formatting; Style; Styling; Insert 1. Introduction This In recent years, the use of the Internet as communi- cation infrastructure for different telecommunication applications has been growing significantly. Because band- width is one o f the most important require ments of these applications, network hardware should support band- width management techniques. Traffic engineering (TE) is a bandwidth management technique that considers different objectives such as maximum throughput, mini- mum congestion and load balancing in the network. TE puts the traffic where network bandwidth is available [1]. TE with the objective of load balancing can reduce maxi mu m l i n k utilizat io n (M LU) a nd increa se b and width efficiency (BWE). Because considerable delay may oc- cur at congested links, reduction of end to end delay can be achieved as a side result of load balancing. Destination -based routing is not flexible for TE, and so it is highly susceptible to congestion. Because of this reason the concept of TE was developed mostly in MPLS-based networks [2,3]. MPLS-based TE can op- timize traffic distribution using dedicated label switch paths (LSP). The capability of explicit routing and arbi- trary traffic splitting are the most important features of MPLS TE. But the MPLS has not been widely deploy Rapid increase in network traffic especially that of new applications which require QoS guarantees, has encour- aged the network providers to apply IP based TE with different objectives. The main idea of IP-based TE is to find a set of weights that optimizes a specific objective function. If the objective function is the total link cost, the constraint of equal cost multipath (ECMP) causes the problem to be NP hard [4]. Different near-optimal heu- ristic algorithms based on local search were proposed to solve this problem [4]. One approach for analyzing the TE problem is formu- lating it with optimization theory problems. If we con- sider load-balancing as an objective of the optimization problem and consider the amount of traffic load on all links that belong to a specific session as the problem outcome, the solution of such problem is the path of each session that results in minimum conge s tion. Measurements in [5] indicate that bottlenecks of the Internet backbone are not only located between ASs but also they exist in intradomain links. The popular intra- domain routing protocol is OSPF. In this paper we present a formulation of the optimization problem that object to provide maximum load balancing. This objec- tive function is use ful in a situation that net wor k entrance is random since increase the probability of new traffic admission. In addition we try to extract the OSPF metric from this problem and therefore reach the load balancing with OSPF routing. These attempts result in a new defi- nition such as equivalent weight set and equivalent con- straints. In this paper we analyze the optimization prob- lem from feasibility perspective and show that a set of link weights that can be embedded as a link metric in OSPF protocol results in optimal or near optimal load balancing. Our simulations show that this method im-  Maximum Load Balancing with Optimized Link Metrics Copyright © 2012 SciRes. JSEA 15 proves bandwidth efficiency and reduces network con- gestion and also leads to a substantial reduction in the end to end delay. 2. Problem Statement First, Different TE objectives lead to different objective functions of optimization problem. We consider load balancing as an objective of traffic engineering so the objective function of the optimization problem is to mi- nimize MLU (maximum link utilization). Consider the linear optimization problem that is called first primal problem (PRIMAL_I) with the following notation. A connected graph is given. is a set of edge capacities and is a set of source- destination p airs for each sessio n . Is the total amount of session traffic. The amount of traffic in link that belongs to session is . So the problem is: ,, :( ,):(, ) ,, , min (1) (2) 0. . (3) 0 (4) i kk i jjii ji jAjjiA k ij ij kK ij MLU Di sourse XXDi destination ow XC MLU X ∈∈ ∈ = −=− = ≤ ≥ ∑∑ ∑ Constraints (2) are flow conservation constraints that are derived from network topology. Constraint (3) ensure that link flows do not violate link capacity and (4) says that li nk flo ws are nonne gative . The PRI MAL_I solution specifies the , and so we have the optimal path with arbitrary splitting for all sessions that minimize MLU. Our objective is to find a practical method suited for IP netwo rks that fo rces the t raffic to go through a set of op- timal paths. To achieve this goal we should find a set of new link metrics such that all paths which are specified by PRIMALI problem can also be obtained by the short- est path algor ithm in regard t o the new metrics. It means that if 0 k ij X> , then l ink should be selected by ses- sion k according to the shortest path algorithm. Here we assume that the shortest path algorithm is OSPF that supports Equal-Cost Multi-Path (ECMP). The load balancing methods introduced in [6,7] are based on primal optimization problem. In this paper we consider the dual optimization problem (DUAL_II) which is obtained with respect to Lagrange Multipliers. In other word we aim to distribute traffic by deter mining the links weight. And It will be shown that t he Lagra nge Multipliers comparable with constraint (3) can be inter- preted as OSPF link metrics that satisfy the load balanc- ing objective. Link metric in OSPF protocol must be an inte ger be tween 1 and 655 35 but we will sho w in secti on IV tha t the La gr an ge Multip lie rs that are o btains fro m the solution of DUAL_II problem and comparable with con- straint (3), do not satisfy this range in general. So the following definition gives us the choice of an alternative weight set. Definition 1: Two weights set { } 1 L ii Ww = = and { } 1 L ii Ww = ′′ = are equivalent with respect to a given graph (,) GNA with L links, if and only if the shortest paths between any arbitrary nodes in G are the same consi- dering any one of these two weight sets. 3. The Dual Problem Before Before Defining the Lagrange multiplayer { } 1 N ii p= comparable with constraint (2) and { } ,(,) ij ij A w ∈ compara- ble with constr a int (3), the Lagrange polynomial is: 0 :( ,):(.) (,) (,,,) k ij X kk i kijji kK iNj i jAjjiA k ijij ij ij AkK LXMLUP W MLUp DXX w XC ≥ ∈∈∈ ∈ ∈∈ =+ −+ +− ∑∑∑ ∑ ∑∑ (5) For more details can be referred to chapter 5 of [9].To achieve the dual problem the following equation should be satisfied for each feasible X and MLU . (,,, )MLULXMLUP W≥ (6) To satisfy (6) we must have: 0 ij w≥ . Now the func- tion (,) gW P is defined as bellow: , (, )min(,, ,) X MLU gWPLXMLUP W= (7) So we have: , (, ) (, ) (, )min () (1) kk ii X MLU k ij jiij k K ijA ij ij ij A gW PpD Xp pw MLUw C ∈∈ ∈ = + −+ +− ∑∑ ∑∑ ∑ (8) Because ij w and k ij X are positive values, we have: (,) 1 (,) 1 kk iiijijij ij k Ki N ijijij ij ijA pDppwandC w gW PppworC w ∈∈ ∈ −≤ = =−∞− ≥≠ ∑∑ ∑ ∑ (9) The dual function is defined to maximize (,)gW P when all ij w are positive values. Equation (10) shows the DUAL_I problem that is the dual function of PRIMAL_I. max .(10) k kk t kK pD ∈ ∑ (11) kk ijij ppw−≤ (, ) 1 (12) ij ij ij A Cw ∈ = ∑  Maximum Load Balancing with Optimized Link Metrics Copyright © 2012 SciRes. JSEA 16 0 (13) k k s p= 0 (14) ij w≥ As the primal and dual problems are linear, strong duality holds and according to complementary slackness in KKT theorem if ˆ k ij X is optimal solution of PRIM- AL_I and { } ˆˆ , k ij ij wp is the optimal solution of DUAL_I we have: ˆ ˆˆˆ .() 0 kk k ij ijij Xp pw −+ = (15) Equation (15) indicates that if session k passes link (, )ij then kk j iij ppw−= . According to theorem 1 in [8] if { } (,) ˆ ij ij A w ∈ is used as a link metric in a shortest path algorithm, all non empt y links ( 0 k ij X> ) will be included among the selected paths by the shortest path algorithm procedure. 4. Practical Requirements { } (,) ij ij A w ∈ that is calculated from the DUAL_I are equal to or greater than zero. But as we mentioned before OSPF link metrics cannot be zero. We show that there exists a weight set equivalent to { } (,) ij ij A w ∈ that can be obtained using the new optimization problem. Proposition 1: consider (,)GNA with weight set { } (,) ij ij A w ∈ and some scalars { } 1 N ii δ = corresponding to each link and node respectively. If we change the link weight to ijijji ww δδ = +− , then the weight set { } (,) ij ij A w ∈ and { } (,) ij ij A w ∈ are equivalent weight sets with respect to (,)GNA [8]. To achieve non-zero weight set we changed the weights of the links according to algorithm 1. Algorithm 1: Step 1: For each session kK∈ assign the scalar set { } 1 N k ii δ = as follows: ● If there exists at least one directed path to node i from source node of session k (k s), the n k i δ is equal to th e length of the longest hop-count non-loopy path from k sto i. ● Else k i δ is equal to zero. Step 2: Assign the max k i k δ as the final scalar i δ Step 3: ● If the 0 ji δδ −≥ then ijijji ww δδ = +− ● Else 1 ij ij ww= + . So according to Proposition 1 and algorithm 1, there exists an equivalent weight set to { } (,) ij ij A w∈ that all of them are greater or equal to one. Thus we can assume . ij ij ij Cw H= ∑ . Theorem 1: consider two optimization p roblems called DUAL_I and DUAL_II. DUAL_I: (,) max . 1 0 0 k k kk t kK kk ijij ij ij ij A k s ij pD ppw Cw p w ∈ ∈ −≤ = = ≥ ∑ ∑ DUAL_II: (,) max . 0 1 k k kk t kK kk ij ij ij ij ij A k s ij pD ppw CwH p w ∈ ∈ ′ ′′ ′ −≤ ′= ′= ′≥ ∑ ∑ If { } (,) ˆ ij ij A w ∈ is an optimal solution of DUAL_I and { } (,) ˆ ij ij A w ∈ ′ is an optimal solution of DUAL_II, the sets { } (,) ˆ ij ij A w ∈ and { } (,) ˆij ij A w∈ ′ are equivalent weight sets with respect to (,)GNA . Proof: Consider the optimization problem PRIM- AL_II. PRIMAL_II: (,) max. . 1 0 0 k k kk t kK kk ijij ij ij ij A k s ij HpD ppw Cw p w ∈ ∈ −≤ = = ≥ ∑ ∑ It is clear that the ij X s which minimizes the objec- tive function of the problem PRIMALL_II are the same as the ones which cause the problem PRIMALL_I to be optimized. The dual of PRIMAL_II is the DUAL_TEMP. DUAL_TEMP: (, ) max . 0 0 k k kk t kK kk ijij ij ij ij A k s ij pD ppw CwH p w ∈ ∈ ′ ′′ ′ −≤ ′= ′= ′≥ ∑ ∑ From complementar y slackness theorem ˆˆˆˆ .() 0 kk k ij ijij Xpp w ′′′ −+ = (16) Since the optimal solutions of the PRIMAL_I and  Maximum Load Balancing with Optimized Link Metrics Copyright © 2012 SciRes. JSEA 17 PRIMAL_II are the same, thus the weight sets { } (,) ˆ ij ij A w ∈ and { } (,) ˆ ij ij A w ∈ ′ are equivalent weight sets. The weight set { } (,) ij ij A w∈is the feasible set of the prob- lem DUAL_TEMP and hold (16). Therefore it is the op- timal solutio n o f t his problem. So we in this way, we were able to obtain optimal weights that do not include any link with weight 0 by limiting the constraint 0 ij w≥ to 1 ij w′≥ . This converts the problem DUAL_TEMP to DUAL_II. Figure 1 shows the fl ow c hart of our method. With ECMP routing a flow arriving at a node is split evenl y ove r the l ink s on the sho rtest paths fro m this node to the destination. It should be mentioned that arbitrary routing is not possible once ECMP in OSPF is used. so in OSPF environment we can never obtain the optimal routing but we can get close to it as much as possible. Objec tive function that is used in [8] is min . The second term in this ob- jective function cause to minimizes (,) k ij ij A X ∈ ∑ in addi- tion to MLU . In this case the weight set resulted from the dual function is { } ij wr+ (where { } (,) ij ij A w ∈ are Lagrange multipliers that correspond to the non-equal constraint). The routing algorithm that we use in this paper is OSPF. This protocol splits the traffic equally among the available shortest paths, so we prefer traffic splitting as much as possible even if it passes through longer paths. As the constant r in the second term pre- vents the flow to go through long paths we assume that 0r= . Figure 1 . Maximum load balancing flow chart. 5. Simulation Results In this section we simulate the OSPF protocol with its default link metrics and with the metrics that are calcu- lated using the optimizatio n problem. A. Scenario I : In fir st scenario the simula tion plat for m is shown in Figur e 2. All links in this network are DS3 with 44.7 Mbps rate. We suppose FIFO as a queuing policy. The session is a VOIP with GSM quality and the average bit rate is 40 Mbps. Node 1 is the source node and node 2 is the desti- nation. Table 1 show the solution of primal problem ( ) which indicate t he paths that mini mize maximum utiliza- tion. Solution of DUAL_I problem is shown in Ta ble 2 and Ta b l e 3 show the solution of DUAL_II problem. Figure 2. Simulation network to pology. Table 1. O pt imum f lows. X12 20 X13 20 X23 0 X24 20 X25 0 X35 20 X54 20 Table 2. The Soluti on of DUAL_ I. w12 0.0056 w13 0.0017 w23 0 w24 0.0056 w25 0 w35 0.0077 w54 0.0017 Table 3. The Solution of DUAL_II. W12 2 .0177 W13 1 .3567 W23 1 .0000 W24 1 .9823 W25 1 .0000 W35 1 .2843 w54 0.0017  Maximum Load Balancing with Optimized Link Metrics Copyright © 2012 SciRes. JSEA 18 Table 1 sho w that t he opti mum pat hs are 1->2->4 and 1->3->5. These paths can obtain in a shortest path algo- rithm regardin g to the weig hts that show in Table 2. Ta- ble 2 and Table 3 are the equivalent weight s with respect to the graph that shows in Figure 2. So we use the sub- optimal weigh set in Table 3 instead of default OSPF link metrics. Figure 3 show tha t in rec ent me thod p acket drop decrease signifi cantly. In fowlloing scenarioes (senario 2-) the simulation plat for m is s ho wn in Fig ur e 4. We co mpare MLU, BWE (Band width Efficiency), Nu mber of Over Utilized Links, IP Traffic Dropped and IP Traffic Received for all scena- rios Figure.3. D ropping traffic in scenario1 for default protocol and new method. Figure 4. Si mulation Network T opology. In fowlloing scenarioes (senario 2-) the simulation plat for m is s ho wn in Fig ur e 4. We co mpare MLU, BWE (Bandwidth Efficiency), Num ber of Over Utilized Links, IP Traffic Dropped and IP Traffic Received for all scena- rios Scenario 2: In this scenario R1 is the traffic source and R13 is the tra ffic destinat ion. Table 4 and Table 5 show the Subo ptimal Link Weights that obt in by DUAL_II . MLU in new method decreases from 91.3 percent to 36.3 percent and BWE increases from 7.6 percent to 10 percent as shown in Table 6. Table 4. Solution of DUAL_ II f or Senario2. W1_2 56.84 W3_6 1.000 W2_1 55.56 W6_3 1.000 W1_3 1.000 W3_7 1.000 W3_1 1.000 W7_3 1.000 W1_4 1.000 W4_9 1.000 W4_1 1.000 W9_4 1.000 W2_5 1.000 W4_8 1.000 W5_2 1.000 W8_4 1.000 W2_11 1.000 W5_12 1.000 W11_2 1.000 W12_5 1.000 W2_3 1.000 W6_11 1.000 W3_2 1.000 W11_6 1.000 W3_4 2.000 W6_10 1.000 W4_3 1.000 W10_6 1.000 Table.5. Solution of D UAL_ II, cont for Senario2. W6_7 55.84 W10_13 1.000 W7_6 1.000 W13_10 1.000 W7_10 1.000 W10_14 1.000 W10_7 1.000 W14_10 1.000 W7_9 1.283 W11_12 1.000 W9_7 1.000 W12_11 1.000 W8_9 1.000 W11_13 1.000 W9_8 1.000 W13_11 1.000 W9_10 1.000 W12_13 1.000 W10_9 1.000 W13_12 1.000 W9_15 2.000 W13_14 1.000 W15_9 1.000 W14_13 1.000 W10_11 1.000 W14_15 1.000 W11_10 1.000 W15_14 1.000 Table 6. MLU and BWE v alue s for Senar io2. Default Algorithm Suboptimal Algorithm M LU 91.3 36.3 BWE 7.6 10 Number of Over Utilized Lin k 0 0 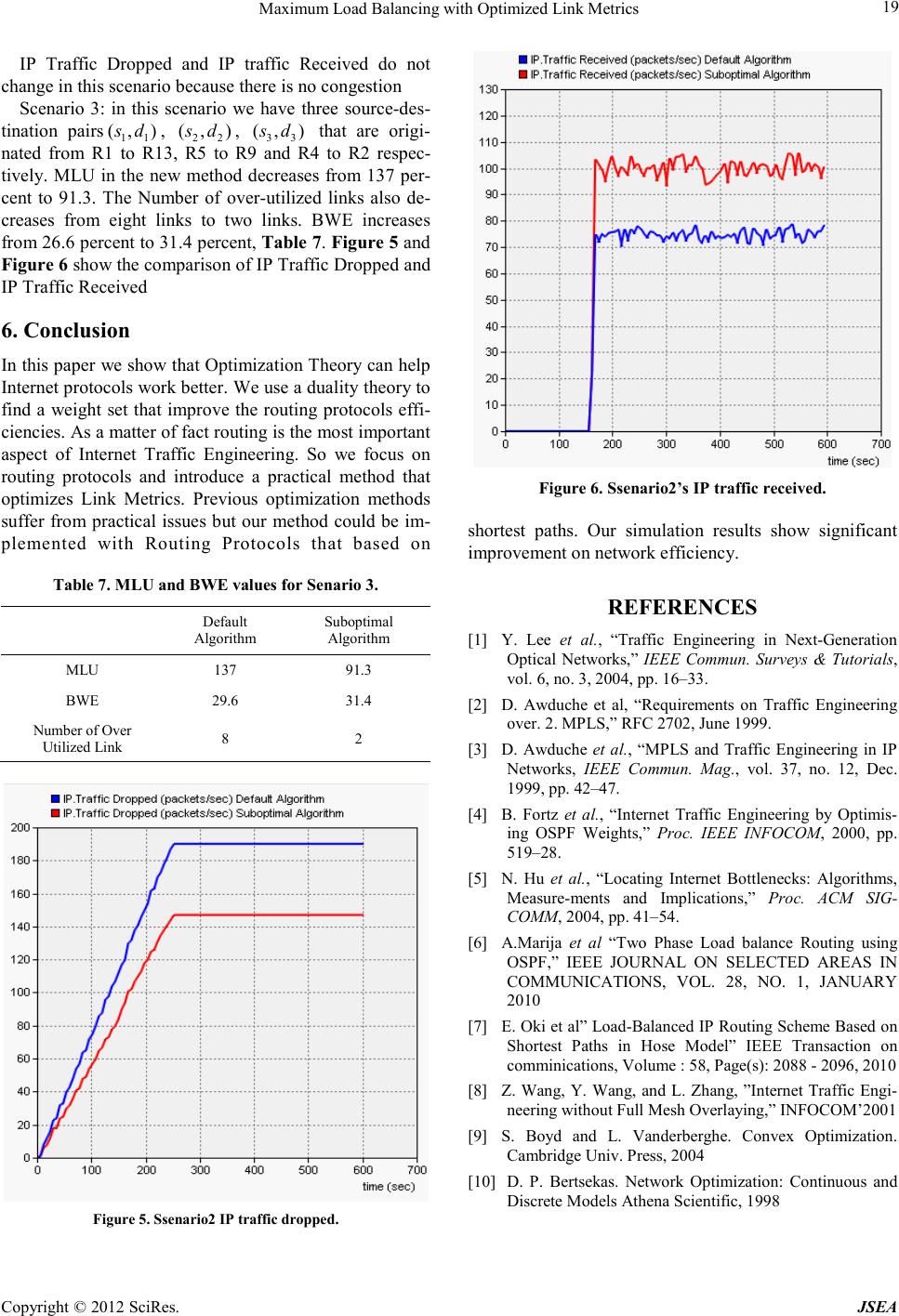 Maximum Load Balancing with Optimized Link Metrics Copyright © 2012 SciRes. JSEA 19 IP Traffic Dropped and IP traffic Received do not change in this scenario because there is no congestion Scenario 3: in this scenario we have three source-des- tination pairs 11 (, ) sd , 22 (, )sd , 33 (, )sd that are origi- nated from R1 to R13, R5 to R9 and R4 to R2 respec- tively. MLU in the new method decreases from 137 per- cent to 91.3. The Number of over-utilized links also de- creases from eight links to two links. BWE increases from 26.6 percent to 31.4 percent, Table 7. F igure 5 and Figure 6 show the comparison of IP Traffic Dropped and IP Traffic Received 6. Conclusion In this paper we show that Optimization Theory can help Internet protocols work better. We use a duality theor y to find a weight set that improve the routing protocols effi- ciencies. As a matter of fact ro uting is the most i mportant aspect of Internet Traffic Engineering. So we focus on routing protocols and introduce a practical method that optimizes Link Metrics. Previous optimization methods suffer from practical issues but our method could be im- plemented with Routing Protocols that based on Table 7. MLU and BWE values for Senario 3. Default Algorithm Suboptimal Algorithm M LU 137 91.3 BWE 29.6 31.4 Number of Over Utilized Link 8 2 Figure 5. Ssenario2 IP traffic dro pped. Figure 6 . Ssenario2’s IP traffic received. shortest paths. Our simulation results show significant improvement on network e fficiency. REFERENCES [1] Y. Lee et al., “Traffic Engineering in Next-Generation Optical Networks,” IEEE Commun. Surveys & Tutorials, vol. 6, n o. 3, 2004, pp. 16 –33. [2] D. Awduche et al, “Requirements on Traffic Engineering over. 2. MPLS,” RFC 2702, June 1999. [3] D. Awduche et al., “MPLS and Traffic Engineering in IP Networks, IEEE Commun. Mag., vol. 37, no. 12, Dec. 1999, pp . 42–47. [4] B. Fortz et al., “Internet Traffic Engineering by Optimis- ing OSPF Weights,” Proc. IEEE INFOCOM, 2000, pp. 519–28. [5] N. Hu et al., “Locating Internet Bottlenecks: Algorithms, Measure-ments and Implications,” Proc. ACM SIG- COMM, 2004, pp. 41–54. [6] A.Marija et al “Two Phase Load balance Routing using OSPF,” IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, VOL. 28, NO. 1, JANUARY 2010 [7] E. Oki et al” Load-Bal anced IP Routin g Scheme Based on Shortest Paths in Hose Model” IEEE Transaction on comminications, Volume : 58, Page(s): 2088 - 2 09 6, 2010 [8] Z. Wang, Y. Wang, and L. Zhang, ”Internet Traffic Engi- neering without Full Mesh Overlaying,” INFOCOM’2001 [9] S. Boyd and L. Vanderberghe. Convex Optimization. Cambrid ge U niv. Pres s, 20 04 [10] D. P. Bertsekas. Network Optimization: Continuous and Discrete M odels Athena Sci entific, 1998 |

