Possibility Fuzzy Soft Expert Set
Maruah Bashir
School of Mathematical Sciences, Faculty of Science and
Technology, Universiti Kebangsaan Malaysia, 43600 UKM
Bangi, Selangor DE, Malaysia
Abdul Razak Salleh
School of Mathematical Sciences, Faculty of Science and
Technology, Universiti Kebangsaan Malaysia, 43600 UKM
Bangi, Selangor DE, Malaysia
Abstract— In this paper we introduce the concept of possibility fuzzy soft expert set .We also define its basic operations,
namely complement, union, intersection, AND and OR, and study some of their properties. Finally, we give an application of this
theory in solving a decision making problem.
Keywords—Fuzzy soft expert set, possibility fuzzy soft set, possibility fuzzy soft expert set
1. Introduction
In 1999 Molodtsov [1] initiated a novel concept of soft set
theory as a new mathematical tool for dealing with
uncertainties . After Molodtsov’s work, some different
operations and application of soft sets were studied by Chen et
al. [2] and Maji et al. [3,4]. Furthermore Maji et al. [5]
presented the definition of fuzzy soft set as a generalization of
Molodtsov’s soft set. Roy and Maji [6] gave an application of
this concept in decision making problem. In 2010 Çağman et
al. introduced the concept of fuzzy parameterized fuzzy soft
sets and their operations [7]. Alkhazaleh et al. [8] generalized
the concept of fuzzy soft set to possibility fuzzy soft set and
they gave some applications of this concept in decision
making and medical diagnosis. They also introduced the
concept of fuzzy parameterized interval-valued fuzzy soft set
[9], where the mapping in which the approximate functions
are defined from fuzzy parameters set to the interval-valued
fuzzy subsets of universal set, and gave an application of this
concept in decision making. Alkhazaleh and Salleh [10]
introduced the concept of soft expert sets where the user can
know the opinion of all experts in one model and gave an
application of this concept in decision making problem. Salleh
et al. [11] introduced the concept of multi paramatriezed soft
set and studied its properties and basic operations. Alkhazaleh
and Salleh [12] introduced the concept of fuzzy soft expert
sets and gave an application of this concept in a decision
making problem. In this paper we introduce the concept of
possibility fuzzy soft expert set which is a combination of
possibility fuzzy soft set and fuzzy soft expert set. We also
define its basic operations namely complement, union,
intersection, AND and OR. Finally,we give an application of
this concept in adecision making problem.
2. Preliminaries
In this section we recall some definitions and properties
regarding soft expert set , fuzzy
soft expert set and possibility fuzzy soft set.
Alkhazaleh and Salleh [10] defined soft expert set and in [12]
Alkhazaleh and Salleh defined a fuzzy soft expert set in the
following way. Let
Ube a universe,E a set of parameters,
and
X
a set of experts (agents). Let Obe a set of opinions,
Z
EXO

 and
A
Z.
Definition 2.1. [12] A pair

,
F
Ais called a soft expert set
over ,U where
F
is a mapping


:
F
APU
and


PU denotes the power set of .U
Definition 2.2. [12] A pair


,
F
Ais called a fuzzy soft expert
set over ,U where
F
is a mapping:
U
F
AI,and
U
Idenotes all fuzzy subsets of .U
Definition 2.3. [12] The complement of a fuzzy soft expert set


,
F
A is denoted by

, c
F
Aand is defined by

, c
F
A=


, Ί
c
F
A where


:Ί
c
F
ApU is a
mapping given by

 
Ί,Ί,
c
F
cF A  where c
is a fuzzy complement.
Definition 2.4. [12] The union of two fuzzy soft expert sets


,
F
Aand


,GB over ,U denoted by



,,
F
AGB

, is
a fuzzy soft expert set

,
H
C where CAB

and
,C






  
,
,
, ,
FifAB
HG ifBA
sFGifAB

 
 








where is an -norm. ss
Definition 2.5. [12] The intersection of two fuzzy soft expert
sets


,
F
Aand


,GB over ,U denoted by




,,,
F
AGB

is a soft expert set


,
H
Cwhere
andCAB

 ,C



Open Journal of Applied Sciences
Supplement：2012 world Congress on Engineering and Technology
208




  
,
,
, ,
FifAB
HG ifBA
tFGifA B

 
 








where is a -norm. tt
The following definitions are due to Alkhazaleh et al. [8].
Definition 2.6. Let

12
,,..., n Uxx x be the universal set of
elements and

12
,,..., m Eee ebe the universal set of
parameters. The pair (,)UE will be called a soft universe. Let
:U
F
EIand

be a fuzzy subset of ,E i.e. :U
EI  ,
where U I is the collection of all fuzzy subsets of U. Let
:UU
F
EII

 be a function defined as follows:




()(), ()
F
e Fexex

 ,
x
U .
Then
F

is called a possibility fuzzy soft set (PFSS in short)
over the soft universe (,).UE For each parameter
  
, (),
ii ii
eFeFe xex

 indicates not only the
degree of belongingness of the elements of U in (),
i
F
ebut
also the degree of possibility of belongingness of the elements
of U in (),
i
F
e which is represented by()
i
e

. So we can
write ()
i
F
e

as follows:
1
1
1
( ),()(),...,,()()
()( )()().
n
ii in
iin
xx
Fee xe x
Fe xFe x

 
 

 
 

Sometime we write
F

as

,.
F
E

If
A
Ewe can also
have a PFSS

,.
F
A

Definition 2.7. Union of two PFSSs
F

and ,G

denoted by
,
F
G



 is a PFSS :UU
H
EII

 defined by
   
(), ,
H
eHexex eE


such that

()(), ()
H
esFeGe and

()(), ()es ee  
where s is an s-norm.
Definition 2.8. Intersection of two PFSSs
F

and ,G

denoted by ,
F
G



 is a PFSS :UU
H
EII

 defined
by
 

 
() ,
H
e Hexex

  ,eE
such that

()(), ()
H
etFeGe and

()(), ()et ee  
where t is a t-norm.
3. Possibility Fuzzy Soft Expert Sets
In this section we generalise the concept of fuzzy soft expert
sets as introduced by Alkhazaleh and Salleh. [12]. In our
generalisation of fuzzy soft expert set, a possibility of each
element in the universe is attached with the parameterization
of fuzzy sets while defining a fuzzy soft expert set.
Definition 3.1. Let


12
,,...,n Uuuu be the universal set of
elements,


12
,,..., m Eee ebe the universal set of
parameters,
X
be a set of experts, and


1agree, 0disagreeO a set of opinions.
Let


Z
EXOand .
A
Z Let :U
F
ZIand

be
a fuzzy subset of ,
Z
i.e. :U
Z
I  , where U I is the
collection of all fuzzy subsets of U. Let :UU
F
ZII


be a function defined as follows:




()(), ()
F
z Fzuzu

 ,.uU
Then
F

is called a possibility fuzzy soft expert set (PFSES in
short) over the soft universe (, ).UZ For each





 


, (),
ii ii
zFzFzu zu

 indicates the degree of
belongingness of the elements of U in (),
i
F
zand also the
degree of possibility of such belongingness which is
represented by()
i
z

. So we can write ()
i
F
z

as follows:
1
1
1
( ),( )(),...,,( )( )
()()()() .
n
ii in
iin
uu
Fzz uz u
Fz uFzu

 








Sometime we write


,
F
Z

as .
F

If
A
Zwe can also
have a PFSES


,.
F
A

Definition 3.2. Let


,
F
A

and

,GB

be two PFSESs
over (,)UZ .


,
F
A

is said to be a possibility fuzzy soft
expert subset (PFSE subset) of


,,GB

and we write




,,,
F
AGB

 if
A
Band ,
A


i.




is a fuzzy subset of

,


ii.


is a fuzzy subset of .FG


Definition 3.3. A possibility agree - fuzzy soft expert
set


1
,
F
A

over U is a possibility fuzzy soft expert subset of


,
F
A

defined as follows :










1
,,, where 1.FAFE X


Definition 3.4. A possibility disagree - fuzzy soft expert
set


0
,
F
A

over Uis a possibility fuzzy soft expert subset of


,
F
A

defined as follows :










0
,,, where 0.FAFEX


2

Definition 3.5. Let

,
F
A

be a PFSES over (,)UZ . Then
the complement of

,
F
A

, denoted by

,c
F
A

is defined
by

   

,, ,
c
F
AcFcA

 
┐┐ ┐ where
c
is a fuzzy soft expert complement and cis a fuzzy
complement.
Definition 3.6. Union of two PFSESs

,
F
A

and

, over ,GB U

denoted by

 
,,,
F
AGB


 is a
PFSES

,
v
H
Cwhere , isCAB defined by

()(),(),
s
C   
and
 
() ,
H
FG C  


where s is an s-norm and  is a fuzzy soft expert union.
Definition 3.7. Intersection of two PFSESs

,
F
A

and

, over ,GB U

denoted by
 
,,,
F
AGB


 is a PFSES

,
v
H
Cwhere , isCAB defined by

()(),(), et eeeC  
and
 
() ,
H
eFeGeeC


where t is a t-norm and  is a fuzzy soft expert intersection.
4. An application of possibility fuzzy
soft expert set
Ahkhazaleh and Salleh [12] applied the theory of fuzzy
soft expert sets to solve a decision making problem. In this
section, we present an application of PFSES in a decision
making problem by generalizing Ahkhazaleh and Salleh’s
algorithm to be compatible with our work.
The problem we consider is as below.
Suppose that electricity board wants to make an
electric generator using waterfalls. Suppose there are
three different locations and they want to take the opinion of
some experts concerning these locations. Let 123 {,, }Uuuu
be a set of locations, 1234 {,, , }Eeeee a set of decision
parameters where

1, 2,3,4
i
eidenotes the decision “Ebb
and tide,” “wind power,” “the power of the regression” and
“solar energy” respectively, and let

,
X
qmbe a set of
experts (two members). Suppose that the electricity
board wants to choose one such location depending on the
parameters. After a serious discussion the committee
constructs the following possibility fuzzy soft expert set:




3 12
1
3 12
2
1
4
,,,1,,0.3,,0.2,,0.3,
0.4 0.2 0.5
,,1,,0.3,,0.4,,0.3,
0.1 0.20.7
,,1,,0
0.9
u uu
FZ eq
u uu
eq
u
eq






  




 
  
  


 





 












3 2
.1 ,,0.4,,0.5,
0.6 0.1
u u




 




 
 







3 12
1
3
12
2
1
3
,,1,,0.1,,0,,0.2,
0.80.3 0.3
,,1,,0.1,,0.5,,0.1,
0.1 00.2
,,1,0.
u uu
em
u
uu
em
u
em


  
 
 
 






 




 
 






3
2
3 12
1
12
2
,0 ,,0 ,,0.1,
10.30.1
,,0,,0.2,,0.3,,0.1,
0.1 0.6 0.2
,,0,,0.5,,0.5,
0.3 0.6
u
u
u uu
eq
uu
eq


  
 
 
  





 




 
 









3
3 12
3
3 12
1
,0.1 ,
0.5
,,0 ,,0.2,,0.3,,0.1,
0.2 0.4 0.5
,,0,,0.3,,0.5,,0.3,
0.3 0.50.4
u
u uu
eq
u uu
em

















 




 
 








 




 








3 12
3
3 12
4
,,0,,0.3,,0.7,,0.3,
0.2 0.40.1
,,0,,0.1,,0.1,,0.1.
0.2 0.3 0.4
u uu
em
u uu
em




 




 
 














 
 
 






The following algorithm may be followed by the electricity
board to determine the best location.
1. Input the PFSES


,.
F
Z
2. Find the highest numerical grade for the agree-PFSES and
disagree-PFSES.
3. Compute the score of each such locations by taking the sum
of the products of these numerical grades with the
corresponding possibility

, for the agree-PFSES which is
denoted by


j
A
and disagree-PFSES denoted by


j
D.
4. Find .
j
jj
s
AD


5. Find ,mfor which max .
mj
s
s

Then m
s
is the highest
score. If mhas more than one value, then any one of them
could be chosen by the electricity board using its option.
Now we use this algorithm to find the best choice for the
electricity board to make an electric generator.
210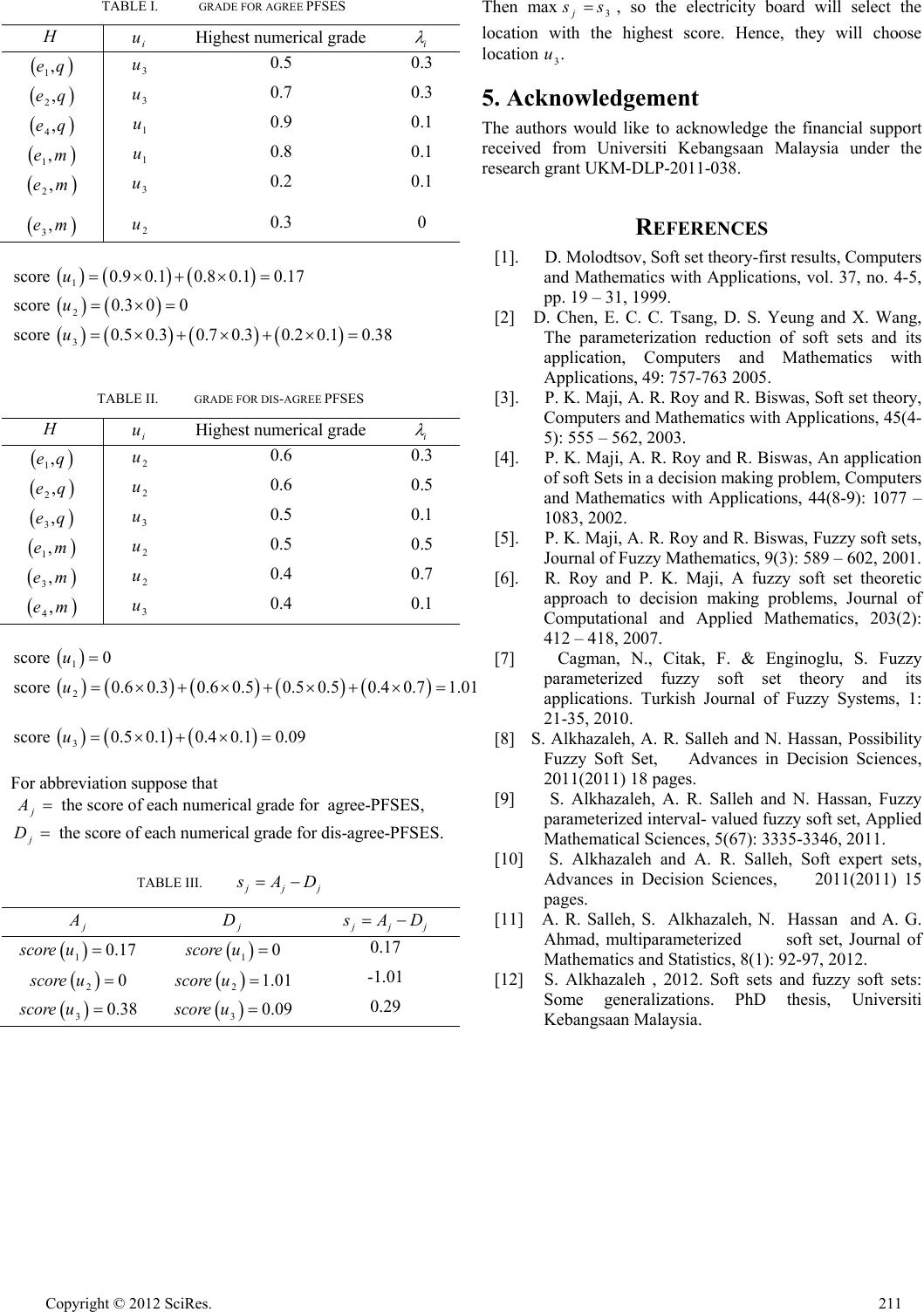

TABLE I. GRADE FOR AGREE PFSES
H
i u Highest numerical grade i


1,eq 3
u 0.5 0.3

2,eq 3
u 0.7 0.3

4,eq 1
u 0.9 0.1

1,em1
u 0.8 0.1

2,em
3
u 0.2 0.1

3,em 2
u 0.3 0
 
1
score 0.90.10.80.10.17u

2
score 0.300u
  
3
score 0.50.30.70.30.20.10.38u
TABLE II. GRADE FOR DIS-AGREE PFSES
H
i
u Highest numerical grade i


1,eq 2
u 0.6 0.3

2,eq 2
u 0.6 0.5

3,eq 3
u 0.5 0.1

1,em2
u 0.5 0.5

3,em 2
u 0.4 0.7

4,em 3
u 0.4 0.1

1
score 0u

2
score 0.60.30.60.50.50.50.40.71.01u 
 
3
score 0.50.10.40.10.09u
For abbreviation suppose that
the score of each numerical grade for agree-PFSES,
j
A
the score of each numerical grade for dis-agree-PFSES.
j
D
TABLE III.
j
jj
s
AD


j
A
j
D
j
jj
s
AD

10.17score u

10score u

0.17

20score u

21.01score u -1.01

30.38score u

30.09score u 0.29
Then max3j
s
s

, so the electricity board will select the
location with the highest score. Hence, they will choose
location 3.u
5. Acknowledgement
The authors would like to acknowledge the financial support
received from Universiti Kebangsaan Malaysia under the
research grant UKM-DLP-2011-038.
REFERENCES
[1]. D. Molodtsov, Soft set theory-first results, Computers
and Mathematics with Applications, vol. 37, no. 4-5,
pp. 19 – 31, 1999.
[2] D. Chen, E. C. C. Tsang, D. S. Yeung and X. Wang,
The parameterization reduction of soft sets and its
application, Computers and Mathematics with
Applications, 49: 757-763 2005.
[3]. P. K. Maji, A. R. Roy and R. Biswas, Soft set theory,
Computers and Mathematics with Applications, 45(4-
5): 555 – 562, 2003.
[4]. P. K. Maji, A. R. Roy and R. Biswas, An application
of soft Sets in a decision making problem, Computers
and Mathematics with Applications, 44(8-9): 1077 –
1083, 2002.
[5]. P. K. Maji, A. R. Roy and R. Biswas, Fuzzy soft sets,
Journal of Fuzzy Mathematics, 9(3): 589 – 602, 2001.
[6]. R. Roy and P. K. Maji, A fuzzy soft set theoretic
approach to decision making problems, Journal of
Computational and Applied Mathematics, 203(2):
412 – 418, 2007.
[7] Cagman, N., Citak, F. & Enginoglu, S. Fuzzy
parameterized fuzzy soft set theory and its
applications. Turkish Journal of Fuzzy Systems, 1:
21-35, 2010.
[8] S. Alkhazaleh, A. R. Salleh and N. Hassan, Possibility
Fuzzy Soft Set, Advances in Decision Sciences,
2011(2011) 18 pages.
[9] S. Alkhazaleh, A. R. Salleh and N. Hassan, Fuzzy
parameterized interval- valued fuzzy soft set, Applied
Mathematical Sciences, 5(67): 3335-3346, 2011.
[10] S. Alkhazaleh and A. R. Salleh, Soft expert sets,
Advances in Decision Sciences, 2011(2011) 15
pages.
[11] A. R. Salleh, S. Alkhazaleh, N. Hassan and A. G.
Ahmad, multiparameterized soft set, Journal of
Mathematics and Statistics, 8(1): 92-97, 2012.
[12] S. Alkhazaleh , 2012. Soft sets and fuzzy soft sets:
Some generalizations. PhD thesis, Universiti
Kebangsaan Malaysia.
