Implementation of LT Code with a Novel Degree
Distribution
Qingxiao Du, Xiaoqin Song, Ying Liu
College of Electronic and Information Engineering,
Nanjing University of Astronautics and Aeronautics
Nanjing, China
[e-mail], [e-mail]
Liping Zhao
Nanjing Telecommunication Technology Institute
Nanjing, China
Abstract—It is known that Luby Transform code (LT code) is the first code fully realizing the digital fountain concept and
provides an efficient scheme to transfer information over different channels. The key to make LT code work well is the degree
distribution used in the encoding procedure. It determines the degree of each encoding symbol. On the basis of robust solition
distribution and optimized degree distribution, a novel degree distribution which has only one parameter is proposed in this paper.
Through computer simulation, the performance of LT code with the novel degree distribution is better than the robust solition
distribution and sparse degree distribution. The conclusion of the research is practically valuable in improving the efficience of
data distribution application.
Keywor ds- LT code; degree distribution; robust solition distribution; sparse degree distribution
1. Introduction
Reliable transmission of data over different channels has
been the subject of many researches. Digital fountain [1] is an
ideal protocol which guarantees both the efficiency and the
reliability of the distribution of bulk data. With the academic
theory became more and more mature, fountain code attracted
increasing attention in many practical applications such as
multicast, downloading in parallel and streaming video [2].
Digital fountain was also widely accepted.
The LT code proposed by Luby [3] was the first practical
realization of fountain code. The algorithm was further
analyzed and optimized so as to improve the efficiency [4]. In
the practical implementations of LT code, random number
generator was employed to determine the degree and neighbors
of an encoding symbol. However, the key to make LT code
work well is the degree distribution used in the encoding
procedure. A good degree distribution should meet the
following two requirements: Firstly, as few encoding symbols
as possible on average are required to ensure successful
recovery of source symbols; Secondly, the average degree of
the encoding symbols shall be as low as possible.
In this paper, we propose a novel degree distribution
scheme which is effective in both theory and practical.
Through computer simulations, it is shown that the novel
degree distribution algorithm performs better than the robust
solition degree distribution and the sparse degree distribution.
The proposed novel degree distribution can then improve the
performance of LT code.
The paper is organized as follows: Section II describes the
encoding and decoding principles of LT codes. Some basic
degree distributions are proposed in Section III. In Section IV,
a novel degree distribution is proposed. In Section V, the
performances of novel degree distribution, robust soliton
distribution and sparse degree distribution are tested and
compared. Finally, the conclusions are drawn in Section VI.
2.Encoding and Decoding Principles
In this section, a brief introduction of the encoding and
decoding of LT code is provided.
A.Encoding of LT code
In LT codes, each encoding symbol is generated and
independent with all the other encoding symbols. Assume that
the number of source symbols is K and the degree of encoding
symbols is equal to d.
The process of generating an encoding symbol is as
follows:
zRandomly choose a degree d according to the degree
distribution ;
zChoose uniformly at random d different source
symbols as neighbors of one encoding symbol;
zXOR the d different source symbols which are chosen
above to generate an encoding symbol.
Repeating the above procedures can generate encoding
symbols one by one.
B.Decoding of LT code
The Belief Propagation (BP) algorithm of LDPC was
researched in [5-6]. However, there is an important difference:
the tanner graph of LDPC code includes one kind of variable
node, while LT code contains two kinds of variable nodes. One
is the information variable nodes which are not transmitted and
have no channel information. The other is encoding variable
nodes which are transmitted over the channel.
This paper is sponsored by University of preresearch funds (NS2012045)
and PLA University of Science and Technology preresearch funds (20110603)
and A Project Funded by the Priority Academic Program Development of
Jiangsu Higher Education Institutions(PAPD).
Open Journal of Applied Sciences
Supplement：2012 world Congress on Engineering and Technology
Cop
y
ri
g
ht © 2012 SciRes.203

For each of the encoding symbols and all relative source
symbols with the encoding symbol, if those symbols take XOR
operation, it results in zero. Therefore, assuming that the
generated matrix of LT code is KN Gu, in which K is the
number of source symbols and N is the number of encoding
symbols, then the pseudo checking matrix is
()
[]
T
NKN
HGI
u
, where
I
is a unit matrix .
Let
,ij
h
denotes the value of i row and j column in the
matrix of H
. Some parameters of BP algorithm are as follows:
^`
,
() :1 =
ml
Lml h
: the set of code positions that
participate in the m-th check equation.
^`
,
() :1
ml
Ml mh
: the set of check positions in which
code position l participates.
,
x
ml
q
: The probability that the value of variable node l is x,
given the information obtained via the check nodes other than
check node m.
,
x
ml
r
: The probability that a check node m is satisfied when
variable l is fixed to a value x and given the information
obtained via the variable nodes other than variable node l.
In the following, binary transmission over an AWGN
channel is assumed. Modulated symbols ()mi are transmitted
over an AWGN channel and () ()
i
rmini 
denote received
symbols where ()ni
is a Gaussian white noise which is
independent and obeys normal distribution
2
(0, ) KV .
Ini t ia li za ti o n
Since the receiver receives only the encoding variable
nodes which are transmitted over the channel, the initial
information of source symbols is zero. For 1, 2,,lK L
,
initialize the priori probabilities of the nodes of source symbols:
10
=1/2, =1/2
ll
pp
(1)
For 1,2, ,lK KKN L , initialize the priori
probabilities of the nodes of encoding symbols
12-101
=(1+exp(-2r/)) ,=1-
lll
ppp V
(2)
For every(, )lm , such that
,
1
ml
h
1100
,,
=, =
ml lml l
qpqp (3)
Message passing
The source symbols and encoding symbols of LT code
are considered variable node to deal with.
Step 1: Bottom-up (horizontal):
For each ,lm
, compute
,ml
r G
,
0
,ml
r
and
1
,ml
r
.
01
,,','
'()\
()
mlml ml
lLml
rqq G



(4)
10
,,,,
(1) / 2,(1) / 2
mlml mlml
rrrr GG  
(5)
Step 2: Top-down (vertical):
For each ,lm
, update the values of
0
,ml
q
ˈ
1
,ml
q
and
normalize:
11 1000
,',, ',
'()\ '()\
,
mllm lmllm l
mMlm mMlm
qp rqpr


(6)
01
,,
1/( )
ml ml
qq D 
(7)
000 0
,,, ,
,
ml mlml ml
qqq q DD
(8)
For each l , compute the posteriori probabilities:
1110 00
,,
() ()
,
llml llml
mMl mMl
qp rqpr


(9)
01
1/( )
ll
qq E 
(10)
110 0
,
lll l
qqqq EE (11)
Decoding judgment
For 1, 2,,lKN L , compute
0
sgn(1/ 2)
ll
Cq 
(12)
And get
12
[, ,,]
KN
CCC C

L
.
The first K
of Care source symbols, and the remainder
of C
are encoding symbols.
The algorithm stops.
3. Some Basic Degree Distribution
Schemes
In practice, the key to make LT code work well is
choosing a good degree distribution.
C.Ideal Solition Distribution [7]

1/ ,1
1/ (1),2,3,,
ISD
Ki
iii iK P

®
¯L
(13)
Ideal soliton distribution ensures that all the release
probabilities are identical to 1/K
at each subsequent step.
Hence, there is one expected ripple generated at each
processing step when the number of encoding symbols is equal
to K . After K processing step, the source symbols can be
ideally recovered.However, ideal soliton distribution works
poorly in practice.
D.Robust Solition Distribution [7]
Define ln(/ )Rc KK G  , c and G are two parameters.
c
Controls the mean of degree distribution.The smaller the
c
,
the greater the probability of low degrees.is the allowable
failure probability of the decoder to recover the source
symbols.In this distribution, we need the help of ideal soliton
distribution.
/(),1,2,,(/) 1
()ln(/)/,(/)
0,
RiKiround KR
iRRKiround KR
else
WG


°
®
°
¯
L
(14)
1
() ()
K
ISD
i
ii EP W 
¦
(15)
204 Cop
y
ri
g
ht © 2012 SciRes.

()(()())/,1,2,,
RSD ISD
iiii K PPWE  L (16)
Robust solition distribution is not only viable but also
practical. It is an improvement of the ideal solition distribution.
E.Sparse Degree Distribution [8-9]

234
1
589 19
65 66
0.008 0.4940.1660.073
0.083 0.056 0.0370.056
0.025 0.003
xxxxx
xxx x
xx
: 
 

(17)
24 8
2
16 3264
( )0.190.340.270.13
0.03 0.01 0.03
xxxx x
xxx
: 

(18)
As mentioned above, 1()x:and 2()x:are two different
sparse degree distribution schemes. The index of x is the
degree and the value which is in front of x
is the probability of
the degree.
F.Optimized Degree Distribution [9]
0.083, 1
0.487, 2
() 0.032, 100
1/ (1),
i
i
ii
ii else
M

°
°
®
°
°
¯
(19)
1
()
K
i
i EM ¦ (20)
()()/ ,1,2,,
OPD
ii iK PME L
(21)
The optimized degree distribution has shown outstanding
performance. It also gives us some valuable references to find
other forms of degree distributions which make LT code work
better.
4. A Novel Degree Distribution Scheme
In this section, on the basis of robust solition distribution
and optimized degree distribution, we proposed a novel degree
distribution scheme.
G.A Novel Degree Distribution
Even more effective degree distributions forms have been
achieved by some researcher. One characteristic of these
degree distribution schemes is that the probability for degree
one is less than the probability for degree two. This ensures
that not too many redundant degree one packets are sent,
resulting in more efficient transmission. However, the ideal
solition distribution itself performs rather poorly, as is well
known. To improve it, we take the first two degree
probabilities as parameters.
The choice of the right parameter values with degree
distribution is very important for a promising performance of
the algothrim. Noted that the spike presented in robust solition
distribution is really necessary, thus we considered a slightly
modified form and an extra parameter for the probability of
degree 100. Finally, we define the rest of our distribution to be
the ideal solition distribution.
Let ln( )Rc KK  , where c is a constant and0c!.
On the basis of robust solition distribution and optimized
degree distribution, a novel degree distribution scheme is then
proposed. The expression of the novel degree distribution is as
follows:
0.083, 1
0.487, 2
( )0.032,100
ln() /,(/)
1/ (1),
i
i
ii
RRKiround KR
ii else
I

°
°
°
®
°
°
°
¯
(22)
1
()
K
i
i EI ¦ (23)
()()/ ,1,2,,
NDD iii K
PIE L (24)
In the novel degree distribution, the allowable failure
probability G
introduced by Luby was removed by
considering the fact that this parameter is only approximation.
In fact, the practical failure probability is much larger than G
.
5. Performance Evalution
In this section, the performance of the novel degree
distribution, the robust solition distribution and the sparse
degree distribution were evaluated and compared. Bit error rate
(BER) is employed as a measure of the performance of degree
distribution schemes.
Definition of BER: Bit error rate is the ratio between the
number of error bits that the decoder decodes the received bits
comparing with source bits and the total number of bits.
Assume that the number of source symbols is 1000, the
channel is AWGN channel and the mode of modulation
adopted is BPSK. Each point is the average value which is
running 100 frames. Simulation results and analysis are as
follows:
H.BER of LT code with novel degree distribution VS. SNR
Figure 1. BER of LT Code with novel degree distribution versus SNR for
transmission over AWGN channel
Cop
y
ri
g
ht © 2012 SciRes.205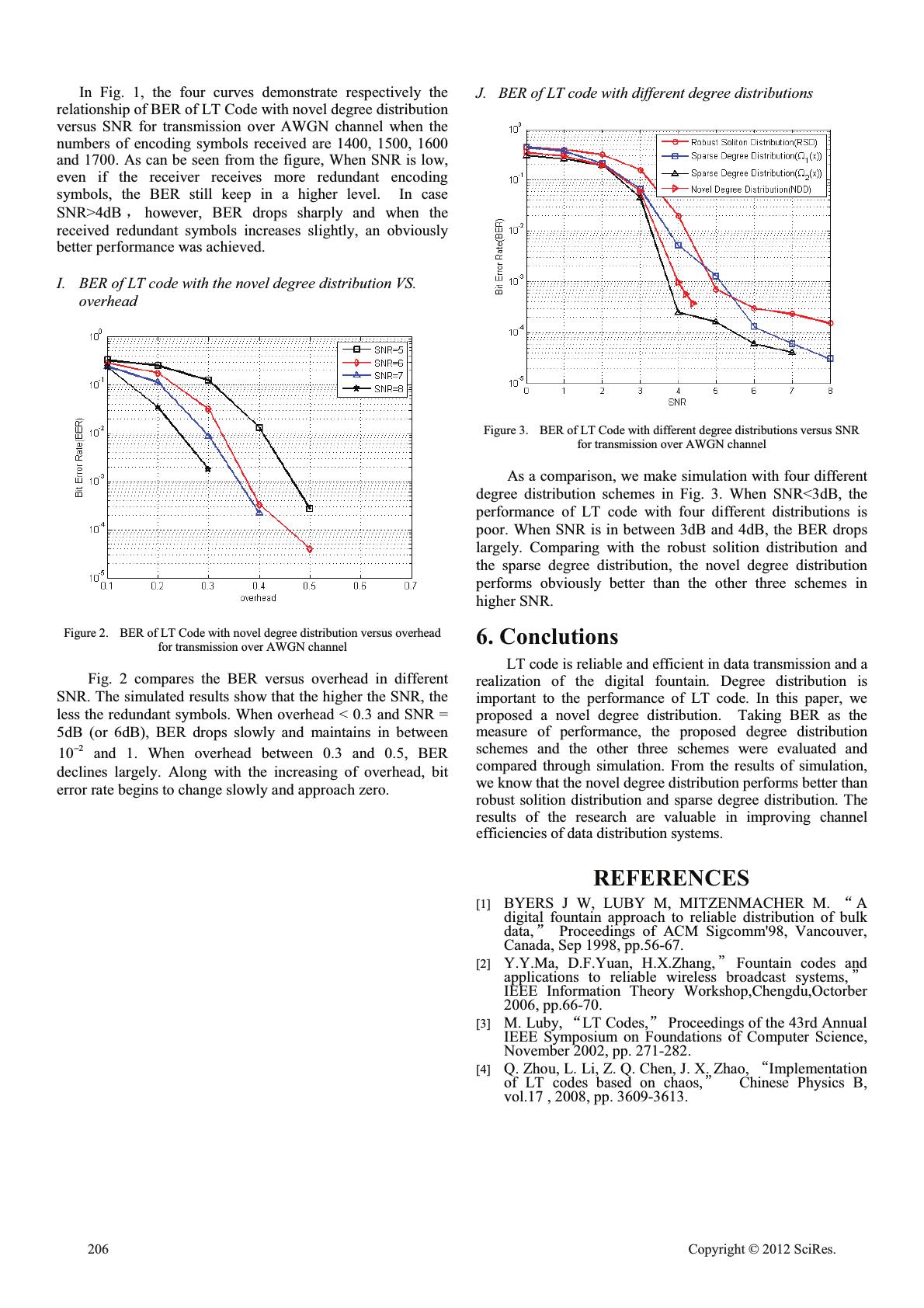

In Fig. 1, the four curves demonstrate respectively the
relationship of BER of LT Code with novel degree distribution
versus SNR for transmission over AWGN channel when the
numbers of encoding symbols received are 1400, 1500, 1600
and 1700. As can be seen from the figure, When SNR is low,
even if the receiver receives more redundant encoding
symbols, the BER still keep in a higher level. In case
SNR>4dB ˈhowever, BER drops sharply and when the
received redundant symbols increases slightly, an obviously
better performance was achieved.
I.BER of LT code with the novel degree distribution VS.
overhead
Figure 2. BER of LT Code with novel degree distribution versus overhead
for transmission over AWGN channel
Fig. 2 compares the BER versus overhead in different
SNR. The simulated results show that the higher the SNR, the
less the redundant symbols. When overhead < 0.3 and SNR =
5dB (or 6dB), BER drops slowly and maintains in between
2
10

and 1. When overhead between 0.3 and 0.5, BER
declines largely. Along with the increasing of overhead, bit
error rate begins to change slowly and approach zero.
J.BER of LT code with different degree distributions
Figure 3. BER of LT Code with different degree distributions versus SNR
for transmission over AWGN channel
As a comparison, we make simulation with four different
degree distribution schemes in Fig. 3. When SNR<3dB, the
performance of LT code with four different distributions is
poor. When SNR is in between 3dB and 4dB, the BER drops
largely. Comparing with the robust solition distribution and
the sparse degree distribution, the novel degree distribution
performs obviously better than the other three schemes in
higher SNR.
6. Conclutions
LT code is reliable and efficient in data transmission and a
realization of the digital fountain. Degree distribution is
important to the performance of LT code. In this paper, we
proposed a novel degree distribution. Taking BER as the
measure of performance, the proposed degree distribution
schemes and the other three schemes were evaluated and
compared through simulation. From the results of simulation,
we know that the novel degree distribution performs better than
robust solition distribution and sparse degree distribution. The
results of the research are valuable in improving channel
efficiencies of data distribution systems.
REFERENC ES
[1] BYERS J W, LUBY M, MITZENMACHER M. ĀA
digital fountain approach to reliable distribution of bulk
data,ā Proceedings of ACM Sigcomm'98, Vancouver,
Canada, Sep 1998, pp.56-67.
[2] Y.Y.Ma, D.F.Yuan, H.X.Zhang,͇Fountain codes and
applications to reliable wireless broadcast systems,͇
IEEE Information Theory Workshop,Chengdu,Octorber
2006, pp.66-70.
[3] M. Luby, ĀLT Codes,ā Proceedings of the 43rd Annual
IEEE Symposium on Foundations of Computer Science,
November 2002, pp. 271-282.
[4] Q. Zhou, L. Li, Z. Q. Chen, J. X. Zhao, ͆Implementation
of LT codes based on chaos,͇ Chinese Physics B,
vol.17 , 2008, pp. 3609-3613.
206 Cop
y
ri
g
ht © 2012 SciRes.

[5] Xiaojing Feng,Wei Zhou, ͆Study on BP decoding
algorithm of LDPC codes,͇ Electronic Test,NO.7
Jul.2009, pp.42-43.
[6] Robert H,Morelos-Zaragoza, ĀThe art of Error
Correcting Coding(Second Edition),ā John
Wiley&Sons,Ltd, 2006, pp.204-206.
[7] Zengqiang Chen,Qian Zhou,āImplementation of LT
codes with a Revised Robust Solition Distribution by
Using Kent Chaotic Map,ā 2010 International
Workshop on Chaos-Fractal Theory and its
Applications,2010, pp.149-153.
[8] Shokrollah A.āRaptor codes,ā.IEEE Transactions on
Information Theory,2006,52(6):2551-2567.
[9] E. Hyytiä, T. Tirronen, J. Virtamo, ͆Optimal the degree
distribution of LT codes with an importance sampling
approach,͇ RESIM 2006, 6th International Workshop on
Rare Event Simulation, Bamberg, Germany,
October,2006, pp.64-73.
Cop
y
ri
g
ht © 2012 SciRes.207