Engineering, 2013, 5, 163-167
doi:10.4236/eng.2013.51b030 Published Online January 2013 (http://www.SciRP.org/journal/eng)
Planning of Anti-Disaster Transf orm er S ubst at i on Based
on NN and PSO
T. Wang1, Q.J. Tang2, X.L. Yang2, X.D. Liu2
1Wenzhou Electric Power Bureau, Wenzhou, China
2 High Voltage Division, Xi’an Jiaotong University, Xi’an, China
Abstract
Recently, the frequent extreme natural disasters made enormous damage to the electric grid leading to blackouts. The
lifeline system aiming at providing continuous power supply for the important load in extreme natural disasters was
designed in that condition. In t his paper , a d evelop ed model for plannin g of the tra nsfor mer substation in lifeli ne syste m
which considered the effect of existing transformer substations, the motivated areas and punishment areas was propo sed.
The Hopfield NN was adopted to solve the feeders and the PSO was adopted to new the locations of the transformer
substa tions based on the feed ers. The planning result not only took fully use of the existing subs tation but also get the
suitable location for new construction which was satisfactory.
Keywords: lifeline system, transformer substation, Hopfield NN, PSO
1. Introduction
In recent years, the globe climate beca me more abnormal
[1]. More and more power equipment accidents caused
by the natural disasters would lead to the blackouts
which affected the normal social activities a lot [2].
Many works have been done to prevent the blackouts
from happening. One major research area was focused on
finding the more suitable topological structure for power
grid to improve the robustness aga inst the dis tur bance [3].
The other was aimed at improving the secondary
controlling and predicting system to minimize the loss
when disaster happened [4][5]. All those work improved
the reliability of the power grid in some way. However,
in 2008, the Wenchuan earthquake in Sichuan province
led to almost 31.8% load shedding which resulted in a
loss of about 10.65 billion yuan directl y [6]. In the same
year, the ice disaster in South China also destroyed over
36000 10kV+ transmission lines and 2000 35kV+
transformer stations which caused large area outage and
a great number of economic losses [2]. The frequent
blackouts caused by the natural disasters exposed the
shortcomings of the defense system that the
improvements on the topological structure and secondary
system couldn’t make up the defect on primary side
completely which meant that the strong primary side was
necessar y [7]. In that conte xt, the State Grid Corporatio n
of China proposed the differentiation construction which
included the lifeline system aiming at providing
continuous power supply for the important load in
extreme natural disasters [8].
As the juncture between the power source and the load,
the distribution of the transformer substation determined
the structure of the power grid, especially in the lifeline
system in which the topological structure was as compact
as possible. The problem of distribution planning could
be divided into two sub-problems that the substations
optimization a nd feeder s op timizatio n [9] . A lot o f work s
had been done to optimize the distribution substation
locations [9]-[13]. Masud defined an approach
employing linear and integer programming to optimize
the capacities and the expansion of the system substation
subject to the constraints of cost, load, voltage, and
reserve requirements [9]. Crawford used operations
research to simultaneously optimize substations and
reliability constraints. Thompson made the further
research by using the branch and bound model which
was utilized a shortest path table to obtain lower bounds
and solutions from a transshipment linear programming
model for upper bounds [11]. With the development on
computer technology, more and more intelligent
algorithms were applied in choosing optimal substation
location. Xi’an Jiaotong University used the Hopfield
neura l net work ( NN) co mbine d wit h gree dy al gorit hm to
find the o p timal fee de r bo unda ry [1 4 ]. T i anj i n Uni versity
and North Electric Power University used the particle
swarm opti mization (PSO) to find the center in the p lane
which would be helpful to get the o ptimal loca tion of the
transform substation [15]-[17]. However, almost all

T. WANG ET AL.
164
those works were focused on expanding the power grid
system and the building new transformer substation.
Little work had been done on how to get the important
transform substation in the existing power grid to
enhance so that the continuous power supply could be
provided to the important load in the extreme disaster.
Actually, in the planning of distribution transformer
substation, the model was aimed at getting a better
economic benefit. Based on that, in this paper, a new
kind of improved model considering the effect of
environment, the differentiation cost between new
construction and reinforce of the existing transformer
substation was proposed. The Hopfield NN and PSO
were combined in model solution by which no potential
substation locations were needed in the calculation
process.
2. The mathematical model
The planning of the distribution transformer substation
aimed at getting best economic benefit. The cost [17]
could be divided into two parts that the cost on
substa tion a nd the cost o n tra nsmi ssion line (a s sho wn in
equation 1):
min sub line
CostCost Cost=+ (1)
Here the cost of substation could be seen as follow:
00
0
00
0
(1+) + (,)(,)
(1+) -1
=(1+) + (,)(,)
(1+) -1
t
newi ikk
t
sub t
existi ikk
t
rr
CSRx yxy
r
Cost rr
CSRx yxy
r
≠



=


(2)
where the (xi, yi) was the coordinate of the transformer
substation in the model; the (xk, yk) was the coordinate of
the exi stin g trans for mer subst atio n; the Cnew was the cost
of new transfor mer substatio n co nstruction; Cexist was th e
cost of existing transformer substation reinforce; r0 was
the discount rate; t was the depreciable life of the
transformer substatio n.
In that model the effect of existing transformer
substations were considered. However, in the lifeline
system, it was excepted that the existing transformer
substation could be used as fully as possible as the cost
of reinforce might had the better economic efficiency
than new construction which meant that the Cnew was
much larger than Cexist. But in same special conditions,
considering the effect of environment, new construction
was necessary sometime as discussed later.
Similarly, the cost of line could be expressed as follo w
considering the effect of existing transformer substation.
To simplify the model, here the effect of existing line
was ignored and the distance between substation and
load was treated as the straight-line distance on the map.
2 00
=1 =1=1 =1
0
2
00
=1 =1=1 =1
0
(1+ )+
(1+) -1
(,)(,)
=(1+ )+
(1+) -1
(,)(,)
l
mn mn
jnewijj ij
l
ij ij
jj kk
line l
mn mn
jexistijj ij
l
ij ij
jj kk
rr
Ld Wd
r
xy xy
Cost rr
Ld Wd
r
xy xy
α
α



≠


×

=


∑∑ ∑∑
∑∑ ∑∑
(3)
22
=(-)+(-)
i jiijiij
dxx yy
(4)
123
22
=cosU
ααα
αθ
××
×
(5)
where r0 was the discount rate; Ljnew was cost of the
transmission line construction per unit length; Ljexist was
cost of the transmission line reinforce per unit length; l
was the depreciable life of the transmission on low
voltage side; dij was the distance between transformer
substation i and load j; α was net loss conversion
coefficient; α1 was electric energy loss coefficient per
unit; α2 was the resistance per unit length; α3 was the loss
hours of the transmission per year; U was the line
voltage; cosθ was the power factor; Wj was the active
power of load.
In the lifeline system, the transformer substation was
excepted to be far away from the high-risk area, such as
the seismic zones, lakes, ice disaster areas and so on. So
here two kind of function [16], the Rew(dik) and the Pun
(dim), were proposed to impro ve the obje ctive function.
The Rew(dik) was defined as the motivational factor that
encouraged the transformer substation to be built in the
suitable area. For example, the suitable area was
simplified to a cycle whose center coordinate was (xk, yk)
and the radius was Dk. It was assumed that the area
closer to the center was more suitable to transformer
substation construction for that a motivate factor would
be added to the objective function while the area outside
the suitable cycle adde d nothing, as shown in equation 6.
2
k ikkik
ik
k ik
Rew(D-d) Dd
Rew( d)0 Dd

×≥

=<

 (6)
where the Rew was the motivate factor; the Dk was the
radius of the cycle; dik was the distance between the
location (xi, yi) and the center (xk, yk).
Similarly, a punitive function was added to the
objection function for those area which was not suitable
to transformer substation construction, as shown in
equation 7.
2
m immim
im
m im
Pun(D-d) Dd
Pun( d)0 Dd
×≥

=<


(7)
Where the Pun was the punitive factor; the Dm was the
radius of the cycle; dim was the distance between the
location (xi, yi) and the center (xm, ym).
Based on the discussion above, the developed model
could be seen as follow.

T. WANG ET AL.
165
min
() ()
n
subline k
n
ik im
m=1 1=
Rew d+PuCost =Costond+C st+
∑ ∑
(8)
However, the model wa s tried to get a bette r eco no mic
efficiency. In other word, the suitable locations of the
trans fo r mer sub stati on s ho uld b e found to ma ke t he va l ue
of Costmin as small as possible. So, the Rew was ne gati ve
while the Pun was positive.
3. The Model Solution with Hopfield NN and
PSO
The problem of planning distribution could be divided
into two aspects that the substations optimization and
feeders optimization. However, those two aspects were
influenced by each other. Based on that condition, the
model solution should be divided into two correlative
steps, too. In this paper, the feeder optimization was got
by Hopfield NN [19] and then the location of transformer
substation was got by PSO based on the feeders
calculated. The iteration method (as shown in figure 1)
was used between those two steps to renew the location
of the transformer substation and the feeders. The
iteration was begun with a series of random substation
coordinate and wouldn’t be ended until the lo cation erro r
between the adjacent two calculations was acceptable.
Start
Random location of
the substation
Feeders optimization by
Hopfield NN
Renew the location of the
substation by PSO
The error was acceptable?
Stop
Yes
Iteration with the
location renewed
No
Figure 1 . Flow Diagram of Algorithm
As the load capacity of the lifeline system was about
20 percent of the total load capacity, the existing
capacity of the transformer substation could meet the
requirement of the existing important load. Considering
the increase of the load, new transformer substation
might be needed whose capacity could be determined
base on the capacity-load ratio and the load factor of the
transformer as discussed in [16]. The capacity of the
substation could be optimized based on the certain
location and the feeders.
As shown in equation 8, when the location of the
transformer s ubstatio n was certain, the Cost s ub, Rew(dik)
and Pun(dim) could be calculated which could be
treated as a constant C. The Costli ne (as shown in
equation 3) could be simplified as following equation.
=1 =1
=(, )
mn
linejjj ij
ij
CostMxyd
∑∑
(9)
Assumed that one load connected to only one
tra ns fo r me r s ubst a ti o n, a c o rre sp o nd e nc e a mo n g n
substation and m loads could be seen in Table 1.
Table 1. The corr e spondence among substat ion and load
B1 B2 … Bm
A1 1 0 … 0
A2 0 1 … 0
… 0 0 … 1
An 0 0 … 0
whe re A i(i=1,2,…,n) wa s the subs tat ion; B i ( i=1,2,…,m)
was the load; 1 r epre sent t he co n nectio n ; 0 rep re se nt
the di sco n nection.
Here, the prob le m co uld be descr ibed a s findi ng the
suitab le corresponding connection to get the minimum
val u e of Costline which could be solved by a Hopfield
NN composed of
nm×
uni ts. T he va lu e o f t he u ni t s
was r eco rde d in t he ma tr ix V (n, m). A n ene rg y
function was defined considering the equation 9 a nd
the constrain t o f the sub statio n capaci ty [14 ][18] .
j=1i=1j=1 =1
2
-/
=1
=-1 +
22
1
+(-1)
21+e
is
m nmn
ijjij ij
i
n
SU
i
AB
E VMdV
C
∆
∑ ∑∑∑
∑
2
（）
(10)
where the Vij wa s t he eleme n t in ma tri x V ( n, m);
=1
=-
n
iij ij
j
S SWV ∆
∑
respect the co nstrai nt o f the
substation;
min
0.001
sj
UW≤×
; A, B, C wa s the
weight coefficients.
Ta ki n g t he der ivation of equation 10 , the dynamical
function of the Hopfield NN was got as follow [14][18].
i=1
-/
-/-/ 2
=1
-1 2
e
1
+(-1)
1+e(1+e )
is
is is
n
ij
ijji j
ij
SU
nj
SU SU
is
du EB
A VMd
dt V
W
Cu
∆
∆∆
∂
=−=− −
∂
∑
∑
（）
(11)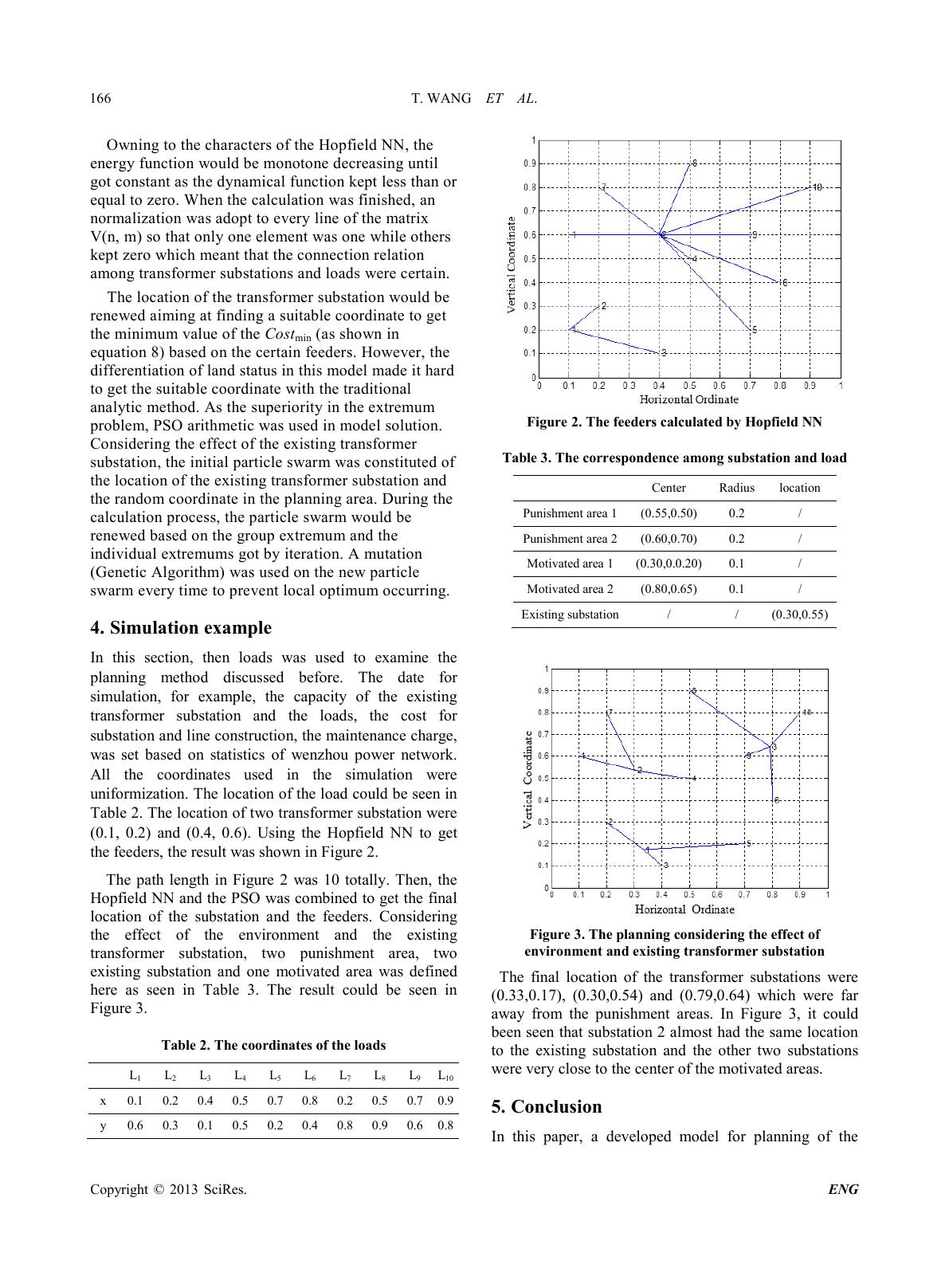

T. WANG ET AL.
166
Owning to t he charact ers o f t he Hop field NN , the
energy function would be monotone decreasing u ntil
got co n st ant as th e d yn a mi c al fu ncti o n ke pt l e ss t han o r
equa l to z e ro . Whe n t he ca l c ul a ti o n wa s fi ni s he d , a n
norma liza tio n wa s ado pt to e ver y li ne o f t he matr ix
V(n, m) so t hat o n l y one el eme n t wa s one wh il e o t hers
kept zero whi c h mea nt t hat t he conne ct ion r ela tion
among transformer substations and loads were certain.
The loc ation o f t he tr an sfo r mer sub sta tio n wou ld b e
renewed aiming at finding a suitable coordinate to get
the minimum value of t he Costmin (as shown in
equation 8) based on the certai n feeders. However, the
differentiation of land status in this model made it hard
to get t he s u itab le co or di na te wit h t he tr adit ional
ana lyt ic me tho d. A s the sup er ior it y in the ex tre mu m
problem, PSO arithmetic was used in model solution.
Co nsider in g t he e ffe ct o f the ex is tin g tr a nsfor mer
substation, the initial particle swarm was constituted of
the l o ca t ion of t he exi st i n g t r a ns fo rmer s ub s tation and
the random coordinate in the planning area. During the
calculation proc es s, t he parti cle s warm would be
renewed based on the group extremum and the
indi vidual e xtremu ms got by itera tion. A muta tio n
(Genetic Algorithm) was used on the new particle
swar m every t i me to p reve nt local optimum occurring.
4. Simulation example
In this section, then loads was used to examine the
planning method discussed before. The date for
simulation, for example, the capacity of the existing
transformer substation and the loads, the cost for
substa tio n a nd line co nstr uct io n, the mai nte nance cha rge,
was set based on statistics of wenzhou power network.
All the coordinates used in the simulation were
uniformization. The location of the load could be seen in
Table 2. The location of two transfor mer substation were
(0.1, 0.2) and (0.4, 0.6). Using the Hopfield NN to get
the feeders, the re sult was sho wn in F igur e 2.
The path length in Figure 2 was 10 totally. Then, the
Hopfield NN a nd the PSO was co mbined to get the final
location of the substation and the feeders. Considering
the effect of the environment and the existing
transformer substation, two punishment area, two
existing substation and one motivated area was defined
here as seen in Table 3. The result could be seen in
Figure 3.
Table 2. The coo r dinates of the loads
L1 L2 L3 L4 L5 L6 L7 L8 L9 L10
x 0.1 0 .2 0.4 0.5 0.7 0.8 0.2 0.5 0.7 0 .9
y 0.6 0 .3 0.1 0.5 0.2 0.4 0.8 0.9 0.6 0.8
Figure 2. The feeders calculated by Hopfield NN
Table 3. The correspondenc e among s ubsta ti o n and loa d
Cen ter Radius location
Punishment area 1 (0.55,0.50) 0.2 /
Punishment area 2 (0.60,0.70) 0.2 /
Motivated area 1 (0.30,0.0.20) 0.1 /
Motivated area 2 (0.80,0.65) 0.1 /
Existing substation / / (0.30,0.55)
Figure 3. The planning c onsidering the e ffect of
environment and existing transformer substation
The final location of the transformer substations were
(0.33,0.17), (0.30,0.54) and (0.79,0.64) which were far
away from the punishment areas. In Figure 3, it could
been seen that substation 2 almost had the same location
to the existing substation and the other two substations
were very close to the center of the motivated areas.
5. Conclusion
In this paper, a developed model for planning of the

T. WANG ET AL.
167
transformer substation in lifeline system was proposed.
In the lifeline system, it was excepted that the existing
transformer substation could be used as fully as possible
to get the better economic efficiency. So in this model,
the effect of existing transformer substations, the
motivated areas and punishment areas were considered.
To solve the model, the Hopfield NN was adopted to
solve the feeders and the PSO was adopted to new the
locations of the transformer substations based on the
feeders. The iteration method was used between those
two steps. By the model and the corresponding algorithm,
the planning of transformer substation not only took fully
use of the existing substation but also get the suitable
location for new construction, whic h was satisfactor y
REFERENCES
[1] Q. Xie and J. Li, “Current situation of natural disaster in
electric power system and countermeasures,” Journal of
Natural Disasters, Vol. 15, No. 4, 2006, pp. 126-131.
[2] AMIN.M, “Toward self-healing energy infrastructure
systems,” IEEE Computer Applications in Power, VOL.
14, NO. 1, 2001, pp: 20-29.
[3] S.Blumsack. “Defining Power Network Zones from
Measures of Electrical Distance,” Conference Record of
the IEEE Power & Society General Meeting, 2009, pp:
1-8.
[4] Y.S. Xue. “Space-time cooperative framework for
defending blackouts: Part Ⅱ reliable information,
quantitative analyses and adaptive controls,” Electric
Power System, 2006, VOL. 30, NO. 2, pp: 1-10.
[5] Y.S. Xue. “Quantitative study of general motion stability
and an example on power system stability,” Jiangsu
Science and Technology Press, 1999.
[6] X.H. Zhang, G.N. Wu, etc. “Effects of Wenchuan
Earthquake on Sichuan Grid,” Modern Electric Power,
2009, VOL. 26, NO. 4, pp: 4-9.
[7] Y.S. Xue, S.Y. Fei, etc. “The Blackouts Defense System
in Extreme Disaster Part Ⅰ new challenge and
introspection,” Automation of Electric Power System,
2008, VOL. 32, NO. 9, pp: 1-6.
[8] M. Lu, D.H. Hu, etc. “Consideration of Strong & Smart
Grid,” Central China Electric Power, 2010, VOL. 12,
NO. 6, pp: 1-7.
[9] Enver Masud. “An Interactive Procedure for Sizing and
Timing Distribution Substations Using Optimization
Techniques,” IEEE Power System, 1973, VOL. PAS-93,
NO. 5, pp: 12 81-1285.
[10] D.I. Sun, D.R. Farris, etc. “Optimal Distribution
Substation and Primary Feeder Planning via the Fixed
Charge Network Formulation,” IEEE Transactions on
Power Apparatus and Systems, 1982, VOL. PAS-101,
NO. 3, pp: 602-609.
[11] D.M Cowford. “A Mathematical Optimization Techniqu e
for Locating and Sizing Distribution Substations and
Deriding Their Opitmal Service,” IEEE Transaction on
Power Apparatus and System s , 1975, VOL. 94, NO. 2, pp:
230-235.
[12] G.L. Thompson. “A Branch and Bound Model for
Choosing Optimal Substation Location,” IEEE
Transactions on Power Apparatus and Systems, 1981,
VOL. 100, NO. 5, pp: 2683-2688.
[13] T.H. Fawzi, K.F. Ali, etc. “A New Planning Model for
Distribution Systems,” IEEE Transactions on Power
Apparatus and Systems, 1983, VOL. PAS-102, NO. 9, pp:
3010-3017.
[14] W.X. Gao, X.J. Luo, etc. “A New Distribution Substation
Planning Algorithm Based on Greedy Algorithm and
Hopfield Neural Network,” Power System Technology,
2004, VOL. 28, NO. 7, pp: 73-76.
[15] T. Zeng. “Research on Substation Planning Based on
Particle Swarm of Culture Algorithm,” Tianjin University,
2008.
[16] Y.W. Zhang. “Optimal Planning for Substation Locating
and Sizing,” Tianjin University, 2 005
[17] H.W. Dai. “Optimal Planning of Distribution Substation
Location and Sizes-model and Algorithm,” International
Journal of Electrical Power and Energy System, 1996,
VOL. 18, NO. 6, pp: 353-357.
[18] F.Shi, X.C. Wang, etc. “30 cases analysis of Matlab
Neural Network,” The Beijing University of Aeronautics
and Astronau t ics Press, 2010.