Paper Menu >>
Journal Menu >>
 Engineering, 2013, 5, 157-162 doi:10.4236/eng.2013.51b029 Published Online January 2013 (http://www.SciRP.org/journal/eng) Copyright © 2013 SciRes. ENG Differential Evolution Immunized An t Colony Optimization Technique in Solving Economic Load Dispatch Prob lem N. A. Rahmat, I. Musirin Universiti Te knologi M ARA, Mala ysia Email: azamrahmat@gmail.com, i_musirin@yahoo.co.uk Received 2013 Abstract Since t he introduction of Ant Colony Optimization (ACO) technique in 1992, the algorithm starts to gain popularity due to its attractive features. However, several shortcomings such as slow convergence and stagnation motivate many re- searchers to stop further implementation of ACO. Therefore, in order to overcome these drawbacks, ACO is proposed to be combined with Differential Evolution (DE) and cloning process. This paper presents Differential Evolution Im- munized Ant Colony Optimization (DEIANT) technique in solving economic load dispatch problem. The combination creates a new algorithm tha t will be termed as Di fferential Evolutio n Immunized Ant Co lony Optimizatio n (DEIANT). DEIANT was utilized to optimize economic load dispatch problem. A comparison was made between DEIANT and classical ACO to evaluate the performance of the new algorithm. In realizing the effectiveness of the proposed tech- nique, IEEE 57-Bus Reliable Test System (RTS) has been used as the test specimen. Results obtained from the study revealed that the proposed DEIANT has superior computation time. Keywords: Ant C olony Optimization (ACO), Differential Evolution (DE), Differential Evolution Immunized Ant Colony Opti- mization (DEIANT) 1. Introduction In 1992, Marco Dorigo introduced a probabilistic algo- rithm known as Ant Colony Optimization (ACO) tech- nique. In his PhD thesis, he described that ACO resem- bles the natural behavior of a colony of ant during their random expedition to find the best path between their nest and food source. The ant will deposit a chemical trace known as pheromone. The pheromone will act as the stimulant to attract more ant s to utilize on the same path. An y l e s s -traveled paths will be for gotte n since the ir pheromone traces has been evaporated. Marco Dorigo empl oyed this behavior into his research to solve the travelling salesmen problem (TSP) [1] . Since, ACO has attracted many researchers to employ the algorithm into their research. Mohd Rozeli Kalil et. al successfully im- plements ACO to gain maximum loadability in voltage control study [2]. Ashish Ahuja and Anil Pahwa [3] stated in their research that ACO significantly minimized the loss i n a distribution s ystem. Moreover, D. Nualhong et. al utilizes ACO in his research to solve the unit co m- mitment problems [4]. However, further research on the algorithm indicates that ACO suffers from several short- comings. H. B. Duan, et al stated in his research that ACO may exper ience stagnation due to its positive feed- back strategy. The researcher also highlighted that the random selection strategy of ACO makes the algorithm sluggish [5]. Another researcher claimed that ACO has slow convergence rate [6-7]. Another attractive optimization technique is the Diffe- rential Evolution (DE). DE was created by Storn and Price in 1995 [8]. As a typical Evolutionary Algorithm (EA), DE was used to sol ve stochastic , no n -differentiable, non-linear, multi-dimensional and population-based op- timization problem [9]. The algorithm was also used to solve a Chebychev Polynomial Fitting Problem during the First Inte rnati o na l Conte s t o n Evo l ut io nary Comp ute r (1st ICE O) in Na goya. As a typi cal Evo lutio n Algo rith m, DE comprises of mutation, crossover, and selection process. In 1997, Storn and Price stated that DE is much better than Simulated Annealing and Genetic Algorithm [10]. As such, DE has become the candidate technique to optimize Neural Network Learning, Radio Network de- sign, multiprocessor synthesis and gas transmission net- work design. Therefore, this paper presents Differential  N. A. RAHMAT, I. MUSIRI Copyright © 2013 SciRes. ENG 158 Evolution Immunized Ant Colony Optimization (DEIANT) technique in solving economic load dispatch problem. The aim of the proposed technique is to alle- viate the slow convergence, and stagnation experienced in the traditional ACO through the application of DE. The performance of DEIANT will be evaluated b y using the algorithm to solve and optimize economic load dis- patch problems. Performance evaluation of the proposed DEIANT revealed that the proposed technique is supe- rior than the traditional ACO in terms of achieving op- timal solutio n and c omputation time. 2. Differential Evolution Immunized Ant Colony Optimization Formulation The capability to achieve fast convergence has been iden- tified as the attractive feature of DE [10]. This feature will be used to compensate the stagnation of ACO algo- rithm. The modification of ACO algorithm will be focus- ing o n the pheromone upda ting rule which is subject ed to cloning, mutation, crossover, and selection process. Fig- ure 1 depi cts the ove rall str ucture and proce sses of Diffe- rential Evolution Immunized Ant Colony Optimization (DEI ANT) algorithm. DEIANT is configured from the combination of original ACO, combined with DE and cloning process. ACO search agent will initialize random tours and deposit pheromone layers. The algorithm will update the pheromone level at each iteration. Cloning process will increase the pheromone amount by generat- ing the exact copies of the pheromone layer. To enhance the pheromone layer, DE will mutate and crossover the pheromone layer, thus increasing the diversity of the pheromone. ACO will evaluate the fitness of the phero- mone layer. ACO Cloning process DE Ant colony deposit pheromone layer Increases pheromone quantity Mutation and crossover process enhance pheromone diversity DEIANT∑ Figure 1. Structural diagram of DEIA NT 2.1. Initialization DEIANT consist of several classical ACO parameters. Therefore, similar to ACO technique, the initial num- ber of ant, nodes, pheromone decay parameter, α, and the initial pheromone level, τ0 will be heuristically in- itializ ed . The maxi mum distance travelled by each ant, dmax, is subjected to a constraint in order to avoid large computation time. dmax is obtained by calculating the longest distance travelled by the ants. Each ant will tour and select the next unvisited node until all nodes have been visited. 2.2. Apply State Transition Rule The next un visit ed no de is chosen according to the state transition rule, s. Each node can only be visited once. The ant that was positio ned at node(r) will go to the next node(s). [ ] [ ] [ ] [ ] ⋅ ⋅ = ∑ β β ητµε ητ )u.r()u,r(J )s.r()s,r( )s,r(P )r(k k (1) 2.3. Apply Local Updating Rule Altering the level of pheromone deposition is done dur- ing the construction of solution. The amount of phero- mone is either increased or decreased to vary the attrac- tiveness of the route via the evaporation rate, ρ. Dorigo stated that parameter ρ is needed to avoid the algorithm converge pre-maturely. The parameter ρ act as a multip- lier and is set between 0 to 1. In thi s rese arc h, t he e vapo- ration rate is set to 0.7, meaning that at every iteration; the pheromone will be reduced by 0.7. 2.4. Pheromone Cloning The cloning process from Artificial Immune System is implemented into DEIANT. The p heromo ne level will be duplicated to increase pheromone population and diver- sity. Figure 2 below depicts the cloning of the original pheromone level. Where υ represents the set of pheromone that will be cloned, and ω represents the c loned pheromone set. Both υ and ω can be written as υ = 1,…,V and ω = 1,…W, respectively. 2.5. Pheromone Mutation The pheromo ne mutation process is used to enhance the pheromone layer over the visited node during ant exploration. The Gaussian Distribution Equation was utilized to mutate the pheromone level as in (2): [ ] υω sr [ ] 12 sr [ ] 11 sr Figure 2 . Pheromone cloning process  N. A. RAHMAT, I. MUS IRI Copyright © 2013 SciRes. ENG 159 ( ) ⋅−⋅+= +max i minjmaxjj,ij,mi f f XX,0NXX β (2) Where j,mi X +: Pheromone mutation function minj X : Smallest visited node maxj X : Largest visited node i f : Distance travelle d by ant max f : Longest distance tr a velled b y ant 2.6. Crossover Crossover operation is implemented to emphasize the diversification vector of the pheromone trail. The mutated pheromone trail and the original one will merge together by applying a binomial distribution known as the crossover operation. In this algorithm, the original and mutated p hero mone level will be resorte d withi n the same matrix. The crossover matrix, Xgi is sorted in des- cending order, as shown below: Where n is the highest pheromone level for the tour, and n-m is the lowes t phero m one level. 2.8 Selection Trial pheromone trail, ρt is the product of the crossover process. The algorithm will now select the required trail accord ing to this rule: ≤ =otherwise , level, pheromone if , t t ρ αρρ ρ Where α is the phero mone deca y parameter. Basically, the selection process will specify the accepta- ble condition to accept the pheromone level. The trail with a higher pheromone leve l will b e selected. The trail with fewer pheromone levels will be discarded. 2.9 Control Variable Calculation The control variable x, is computed by applying the fol- lowing equation: Where: d : distance for every ants tour dmax : maximum distance for every ants tour xmax : maximum of x Variable x will become the multiplier to calculate the objective function. In this research, variable x is multip- lied with the co s t fu nctio n (7). 2.10 Global Updating Rule After all ants have finished performing their random ex- ploratio n, the best ant of the colony will be selected . The best ant i s ca rryi ng t he d at a o f the b e s t to ur , and t hu s, t he data will be stored. The following equation is applied to update the pheromone level glo bally: ( )()( ) )s,r(.s,r1s,r τ∆ατατ +−← (6) The globally best tour will be selected as the first node of the next iteration. 2.11 End Condition The DEACO algorithm will halt the iteration when the maximum number of iteration (tmax) has been reached and all ants have completed their tours. If a b etter path is discovered, it will be used as the reference. Only o ne an t will find the optimal pa th. 3. Economic Load Dispatch Formulation Economic load dispatch is the operation of determining the optimal output that must be produced by the genera- tion facilities to feasibly satisfy the load demand [12]. Therefore, the key objective of economic load dispatch is to reduce the operati ng cost of e ach generating unit in the power system. The operation cost can be calculated by utilizing equation (7): ∑ = Ng i ii )P(F cost (7) Where Ng is the number of generating unit. Fi(Pi) is the cost function, and Pi is the real power output of the unit I, measured in MW. Fi(Pi) is usually approximated by a quadratic function: cPbPa)P(F ii 2 iiii ++= (8) max max x d d x⋅= (5) −− − = mn1n 1nn Xgi (3) (4) 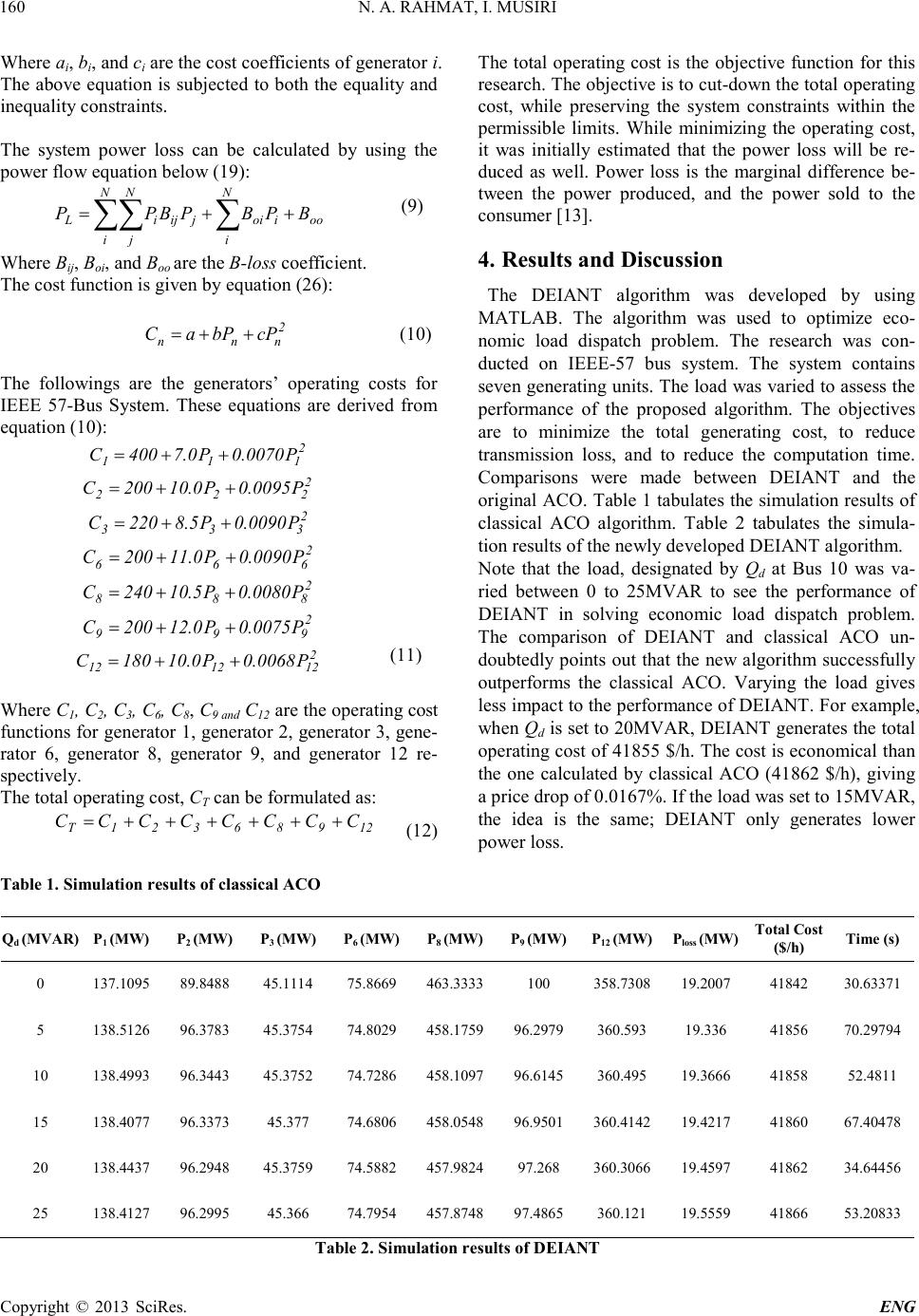 N. A. RAHMAT, I. MUSIRI Copyright © 2013 SciRes. ENG 160 Where ai, bi, and ci are the cost coefficients of generator i. The above equation is subjected to both the equality and inequality constraints. The system power loss can be calculated by using the po wer flow equation below (19): ∑∑ ∑ N i N j N i ooioijijiL BPBPBPP ++= (9) Where Bij, Boi, and Boo are the B-loss coefficient. The cost function is given b y equa tion (26): 2 nnn cPbPaC ++= (10) The followings are the generators’ operating costs for IEEE 57-Bus System. These equations are derived from equa tion (10): 2 111 P0070.0P0.7400C++= 2 222 P0095.0P0.10200C++= 2 333 P0090.0P5.8220C++= 2 666 P0090.0P0.11200C++= 2 888P0080.0P5.10240C++= 2 999 P0075.0P0.12200C++= 2 121212 P0068.0P0.10180C++= (11) Where C1, C2, C3, C6, C8, C9 and C12 are the oper ating cost functi ons for ge nerato r 1, gene rator 2, ge nerator 3, gene- rator 6, generator 8, generator 9, and generator 12 re- spectively. The total operating cost, CT can be formulated as: 12986321TCCCCCCCC ++++++= (12) The total operating cost is the objective function for this research. The objective is to cut-down the total operating cost, while preserving the system constraints within the permissible limits. While minimizing the operating cost, it was initially es ti mated that the power loss will be re- duced as well. Power loss is the marginal difference be- tween the power produced, and the power sold to the consumer [13]. 4. Results and Discussion The DEIANT algorithm was developed by using MATLAB. The algorithm was used to optimize eco- nomic load dispatch problem. The research was con- ducted on IEEE-57 bus system. The system contains seven gene rating un its. The load was varied to assess the performance of the proposed algorithm. The objectives are to minimize the total generating cost, to reduce transmission loss, and to reduce the computation time. Comparisons were made between DEIANT and the original ACO. T able 1 tabulates the si mulatio n results o f classical ACO algorithm. Table 2 tabulate s the simula- tion results of the newly developed DEIANT algorithm. Note that the load, designated by Qd at Bus 10 was va- ried between 0 to 25MVAR to see the performance of DEIANT in solving economic load dispatch problem. The comparison of DEIANT and classical ACO un- doubtedly points out that the ne w algorithm successfully outperforms the classical ACO. Varying the load gives less impac t to the performance of DEIANT. For example, when Qd is set to 20MVAR, DEIANT generates the total operating cost of 41855 $/h. T he cost is economical than the one calculated by classical ACO (41862 $/h), giving a price drop of 0.0167%. If the load was set to 15MVAR, the idea is the same; DEIANT only generates lower power loss. Table 1. Simulati o n results of classical ACO Qd (MVAR) P1 (MW) P2 (MW) P3 (MW) P6 (M W) P8 (MW) P9 (MW) P12 (MW) Plos s (MW) Total Cost ($/h) T ime (s) 0 137.1095 89.8488 45.1114 75.8669 463.3333 100 358.7308 19.2007 4 1842 30.63371 5 138.5126 96.3783 45.3754 74.8029 458.1759 96.2979 360.593 19.336 41856 70.29794 10 138.4993 96.3443 45.3752 74.7286 458.1097 96.6145 360.495 19.3666 41858 52.4811 15 138.4077 96.3373 45.377 74.6806 458.05 48 96.9501 360.4142 19.4217 41860 67.40478 20 138.4437 96.2948 45.375 9 74.5882 457.9824 97.268 360.3066 19.4597 41862 34.64456 25 138.4127 96.2995 45.366 74.7954 457.87 48 97.4865 360.121 19.5559 41866 53.20833 Table 2. Simulation results of DEIANT 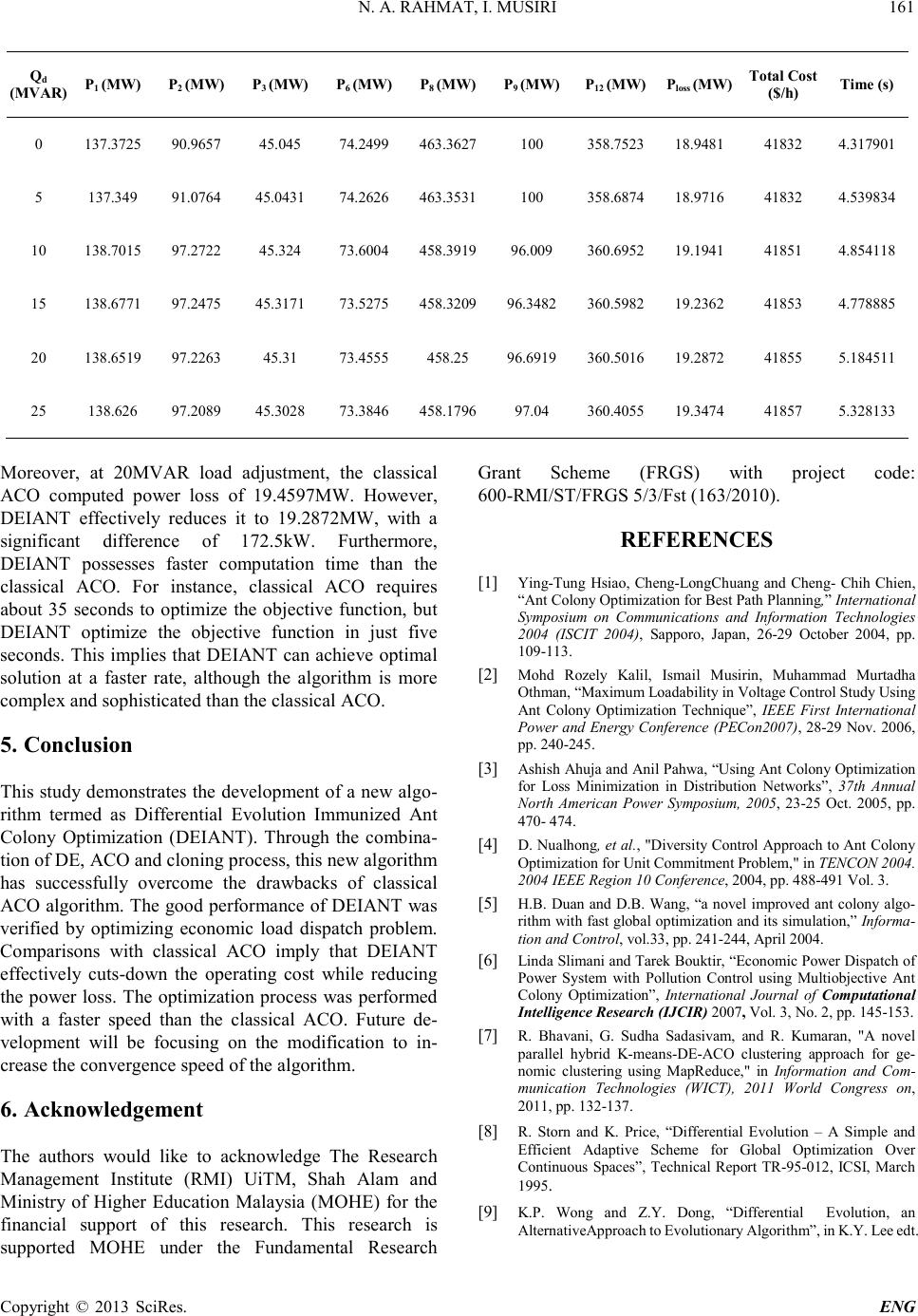 N. A. RAHMAT, I. MUS IRI Copyright © 2013 SciRes. ENG 161 Qd (MVAR) P1 (MW) P2 (MW) P3 (MW) P6 (MW) P8 (MW) P9 (MW) P12 (MW) Ploss (MW) Total Cost ($/h) Time ( s) 0 137.3725 90.9657 45.045 74.2499 463.3627 100 358.7523 18.9481 41832 4.317901 5 137.349 91.0764 45.0431 74.2626 463.3531 100 358.6874 1 8.9716 41832 4 .539834 10 138.7015 97.2722 45.324 73.6004 458.3919 96.009 360.6952 19.1941 41851 4.854118 15 138.6771 97.2475 45.3171 73.5275 458.3209 96.3482 360.5982 19.2362 41853 4.778885 20 138.6519 97.2263 45.31 73.4555 458.25 96.6919 360.5016 19.2872 41855 5.184511 25 138.626 97.2089 45.3028 7 3.3846 458.1796 97.04 360.4055 19.3474 41857 5.328133 Moreover, at 20MVAR load adjustment, the classical ACO computed power loss of 19.4597MW. However, DEIANT effectively reduces it to 19.2872MW, with a significant difference of 172.5kW. Furthermore, DEIANT possesses faster computation time than the classical ACO. For instance, classical ACO requires about 35 seconds to optimize the objective function, but DEIANT optimize the objective function in just five seconds. This implies that DE IANT can achieve optimal solution at a faster rate, although the algorithm is more complex and sophisticated than the cla ssic al A CO. 5. Conclusion This study demonstrates the d evelop ment of a new al go- rithm termed as Differential Evolution Immunized Ant Colony Optimization (DEIANT). Through the combina- tion of DE, ACO and cloning process, this new algor ith m has successfully overcome the drawbacks of classical ACO algorith m. T he good performance of DEIANT was verified by optimizing economic load dispatch problem. Comparisons with classical ACO imply that DEIANT effectively cuts-down the operating cost while reducing the power loss. The optimizatio n process was performed with a faster speed than the classical ACO. Future de- velopment will be focusing on the modification to in- crease the convergence speed of the algorithm. 6. Acknowledgement The authors would like to acknowledge The Research Management Institute (RMI) UiTM, Shah Alam and Ministry of Higher Education Malaysia (MOHE) for the financial support of this research. This research is supported MOHE under the Fundamental Research Grant Scheme (FRGS) with project code: 600-RMI/ST/FRGS 5/3/Fst (163/2010). REFERENCES [1] Ying-Tung Hsiao, Cheng-LongChuang and Cheng- Chih Chien, “Ant Colony Optimization for Best Path Planning,” International Symposium on Communications and Information Technologies 2004 (ISCIT 2004), Sapporo, Japan, 26-29 October 2004, pp. 109-113. [2] Mohd Rozely Kalil, Ismail Musirin, Muhammad Murtadha Othman, “Maximum Loadability in Voltage Control Stud y Using Ant Colony Optimization Technique”, IEEE First International Power and Energy Conference (PECon2007), 28-29 Nov. 20 06, pp. 240-245. [3] Ashish Ahuja and Anil Pahwa, “Using Ant C olony Opti miza tion for Loss Minimization in Distribution Networks”, 37th Annual North American Power Symposium, 2005, 23-25 Oct. 2005, pp. 470- 474. [4] D. Nualhong, et al., "Diversi ty Control App roach to Ant Colon y Optimization for Unit Commitmen t Prob lem," in TENCO N 2 00 4. 2004 IEEE Region 10 Conference, 2004, pp. 488-491 Vol. 3. [5] H.B. Duan and D.B. Wang, “a novel improved ant colony algo- rithm with fast global optimization and its simulation,” Informa- tion and Contro l, vol.33, pp. 241-244, April 2004. [6] Lind a Slimani and Tarek Boukt ir, “Econom ic Power Dispa tch of Power System with Pollution Control using Multiobjective Ant Colony Optimization”, International Journal of Computational Intelli gence Resear ch (I JCI R) 2007, Vol. 3, No. 2, pp. 1 45-153. [7] R. Bhavani, G. Sudha Sadasivam, and R. Kumaran, "A novel parallel hybrid K-means-DE-ACO clustering approach for ge- nomic clustering using MapReduce," in Information and Com- munication Technologies (WICT), 2011 World Congress on, 2011, pp. 132-137. [8] R. Storn and K. Price, “Differential Evolution – A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces”, Technical Report TR-95-012, ICSI, March 1995. [9] K.P. Wong and Z.Y. Dong, “Differential Evolution, an AlternativeApproach to Evolutionary Algorithm”, in K.Y. Lee edt.  N. A. RAHMAT, I. MUSIRI Copyright © 2013 SciRes. ENG 162 Intelligent Optimization and Control for Power Systems, IEEE Publi shing , invited cha pter, No v. 200 5. [10] Storn R., Price K.: ‘Differential Evolution – A Simple and Effi- cient Adaptive Scheme For Global Optimization Over Continu- ous Spa ce”, Jou rnal of Globa l Optimization, 1997. [11] N. A. Rahmat, I. Musirin (2012). Differential Evolution Ant Colony Opt im iza tion Tech niqu e (DE ACO) In S olvi n g Ec onom ic Load Dispatch Problem. IEEE Internation Power Engineering and Optimization. [12] S. M. V. Pandian and K. Thanus hkodi, "Solvin g Economic Load Dispatch Problem Considering Transmission Losses by Hybrid EP-EPSO Algori thm for Solvin g Both S mooth and Non -Smooth Cost Fu nction ," Intern ational Journal of Co mputer and Electric- al Engineering, vol. 2, 2010 [13] M. Basu, “Artificial Immune System for Dynamic Economic dispatch,” Electrical Power and Energy System, vol. 33, pp. 131-136, 7 June 2010 |

