 Engineering, 2013, 5, 108-114 doi:10.4236/eng.2013.51b020 Published Online January 2013 (http://www.SciRP.org/journal/eng) Copyright © 2013 SciRes. ENG Seasonal Regression Mod els f or Elect ricit y Consumption Characteristics Analysis Yusri Syam Akil1,2, Hajime Miyauchi1 1Department of Frontier Technology for Energy and Devices, Kumamoto University, Kumamoto, Japan 2Department of Electrical Engineering, Hasan uddi n Univer s ity, Makassa r, Indo nesi a Email: yusuri@st.c s.ku mamoto-u.ac.jp , miyauchi@c s.kuma moto -u.ac.jp Received 2013 Abstract This paper presents seasonal regression models of demand to investigate electricity consumption characteristics. Elec- tricity consumption in commercial areas in Japan is analyzed by using meteorological variables, namely temperature and relative humidity. A dummy variable for holidays is also considered. We have developed models for two levels of period to analyze demand characteristics, that is, half year models and seasonal models. Some options for each model are calculated and validated by statistical tests to obtain better models. As r esul t s, hal f year and se asonal models present explicit information about how the variables affect the demand differently for each period. These specific information help in analyzing characteristics of studied commercial demand. Keywords: Commercial Area; Demand Characteristics; Regression Model; Seasons; Relative Humidit y; T e mperature 1. Introduction In general, electricity consumption analyses such as cha- racteristics investigation and forecasting can provide much information related to the time variance of demand. The result of demand analysis is useful for electric utili- ties in many aspects, for instanc e, to mana ge and control their systems more effective. Therefore, it is valuable to analyze an electricity demand in detail through develop- ment of demand models. A number of methods can be used for a demand analysis, and one of them is regres- sion analysis. As a tool, a regression model needs a number of data (dependent and explanation variables). The implementation of proper explanation variables is req uir ed to ge t a go od model. As an explanation variable, meteorological parameters such as temperature, humidity, wind speed, and so on, are commonly used and con- firmed electricity demand effectively. Prior studies which employed meteorological parameters and regres- sion models for electricity demand can be found in ref- erences such as [1-4]. Reference [1] develops a demand model using a stepwise procedure to forecast Spanish daily electricity demand. Reference [2] develops regres- sion equations to analyze electricity consumption for residential area in Hong Kong by using climatic and economic variables. Reference [3] develops the model of electricity consumption for residential area in Bangkok Metrop o lis and analyzes e ffect of climatic and economic factors for demand. Meanwhile, in [4], authors have de- veloped two statistical models for demand in Greece, namely dai ly a nd mont hly model s to for ecast d emand up to 12 months ahead (mid-term demand). As electricity demand may differ to time [2,3] and place generally, we have an interest to analyze demand characteristics for commercial area in a typical city in Japan by developing demand models. This study also aims to find the electricity consumption characteristics in Japan. We analyze demand characteristics based on seasonal periods for commercial area in Japan. To achieve the aim, two demand model of two period levels based on different time length, namely half year models (CTEChy1, and CTEChy2) and seasonal models (CTECSM, CTECA, CTECW, and CTECS) are proposed to reveal further demand characteristics by regression analysis. They are developed from an initial model (CTEC) that is derived from all data (whole period) with the same explanation variables and statistical validation processes. In the context of this study, the application of regression approach is effective enough. Beside simple in composing the models, the obtained regression coefficients and statistics contain specific information about the direct relationship between variables and demand. It may be useful to draw a seasonal strategy and to meet demands in maintaining power system performance. 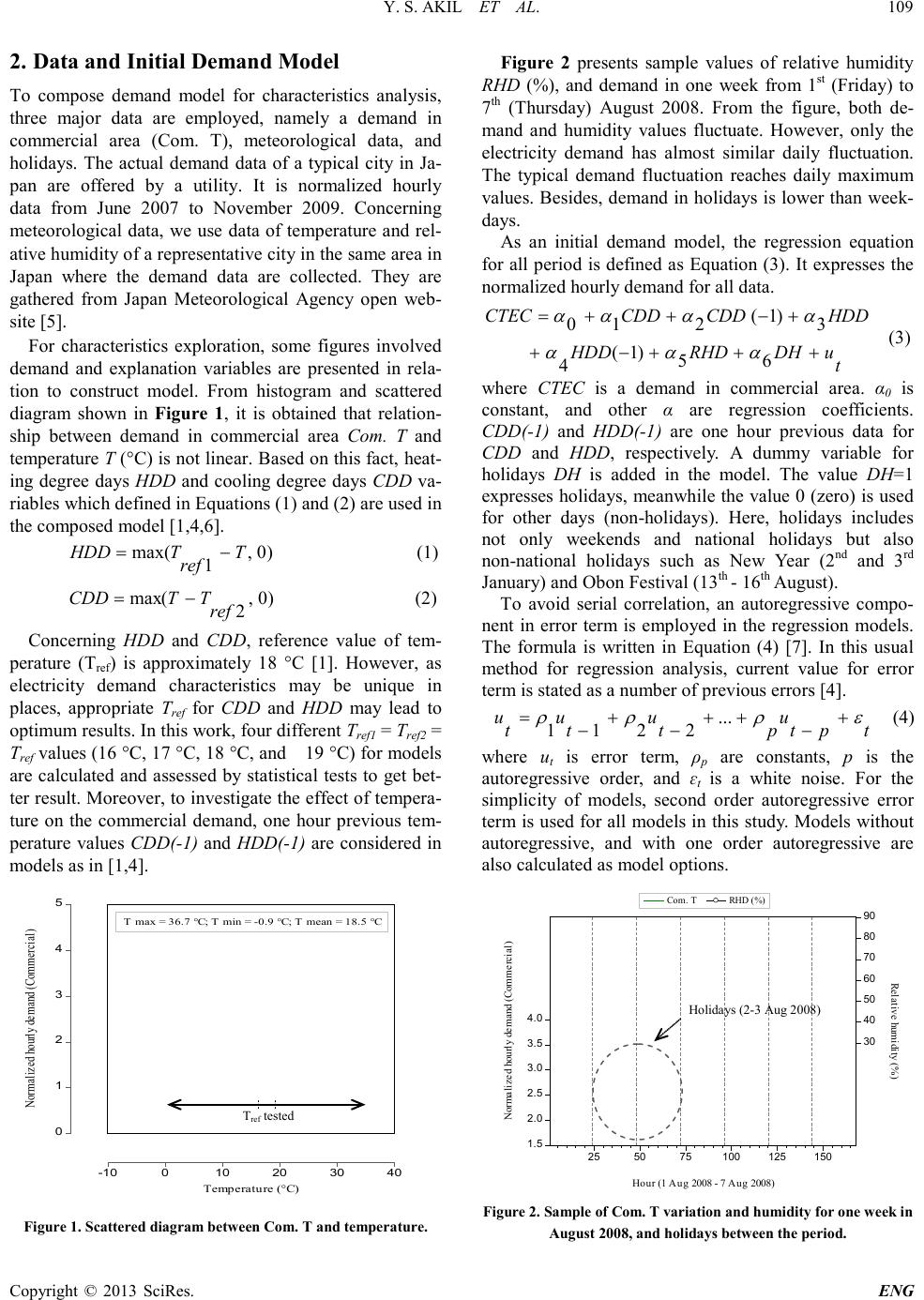 Y. S. AKIL ET AL. Copyright © 2013 SciRes. ENG 0 1 2 3 4 5 Normalized hourly demand (Commercial) -10 010 20 30 40 Temperature (°C) T max = 36.7 °C; T min = -0.9 °C; T mean = 18.5 °C Tref tested 1.5 2.0 2.5 3.0 3.5 4.0 30 40 50 60 70 80 90 255075 100 125 150 Com. TRHD (%) Normalized hourly demand (Commercial) Relative humidity (%) Hour (1 Aug 2008 - 7 Aug 2008) 2. Data and Initial Demand Model To compose demand model for characteristics analysis, three major data are employed, namely a demand in commercial area (Com. T), meteorological data, and holidays. The actual demand data of a typical city in Ja- pan are offered by a utility. It is normalized hourly data from June 2007 to November 2009. Concerning meteorological data, we use data of temperature and rel- ative humidit y of a representative city in the same area in Japan whe r e the demand data are collected. They are gathered from Japan Meteorological Agency open web- site [5]. For characteristics exploration, some figures involved demand and explanation variables are presented in rela- tion to construct model. From histogram and scattered diagram shown in Fig ure 1, it is obtained that relation- ship between demand in commercial area Com. T and temperature T (° C) is not linear. B ased on this fact, heat- ing degree days HDD and cooling degree days CDD va- riables which defined i n Equations (1) and (2) are used in the composed model [1,4,6]. (1) (2) Concerning HDD and CDD, reference value of tem- perature (Tref) is approximately 18 °C [1]. However, as electricity demand characteristics may be unique in places, appropriate Tref for CDD and HDD may lead to optimum res ul ts. In t his work, fo ur differ ent Tref1 = Tref2 = Tref values (16 °C, 17 °C, 18 °C, and 19 °C) for models are calculated and assessed by statistical tests to get bet- ter result. Moreover, to i nvestigate the effect of te mpera- ture on the commercial demand, one hour previous tem- perature values CDD(-1) and HDD(-1) are considered in models as in [1,4]. Figure 1. Scattered diag ra m betwe en Com. T and temperature. Figure 2 presents sample values of relative humidity RHD (%), and demand in one week from 1st (Friday) to 7th (Thursday) August 2008. From the figure, both de- mand and humidity values fluctuate. However, only the electricity demand has almost similar daily fluctuation. The typical demand fluctuation reaches daily maximum values. Besides, demand in holidays is lower than week- days. As an initial demand model, the regression equation for all period is defined as Equation (3). It expresses the normalized hourly demand for all data. t uDHRHDHDD HDDCDDCDDCTEC +++−+ +−++= 6 5 )1( 4 3 )1( 2 10 ααα αααα (3) where CTEC is a demand in commercial area. α0 is constant, and other α are regression coefficients. CDD(-1) and HDD(-1) are one hour previous data for CDD and HDD, respectively. A dummy variable for holidays DH is added in the model. The value DH=1 expresses holidays, meanwhile the value 0 (zero) is use d for other days (non-holidays). Here, holidays includes not only weekends and national holidays but also non-national holidays such as New Year (2nd and 3rd Januar y) and Obon F est ival (13th - 16th August). To avoid serial correlation, an autoregressive compo- nent in error term is employed in the regression models. The formula is written in Equation (4) [7]. In this usual method for regression analysis, current value for error term is stated as a number of previous errors [4]. tpt u pt u t u t u ερρρ + − ++ − + − =... 2211 (4) where ut is error term, ρp are constants, p is the autoregressive order, and ɛt is a white noise. For the simplicity of models, second order autoregressive error term is used for all mode ls in this st udy. Models without autoregressive, and with one order autoregressive are also calculated as model options. Figure 2. Sample of Com. T variation and humidity for one week in August 2008, and holi days between the peri od. 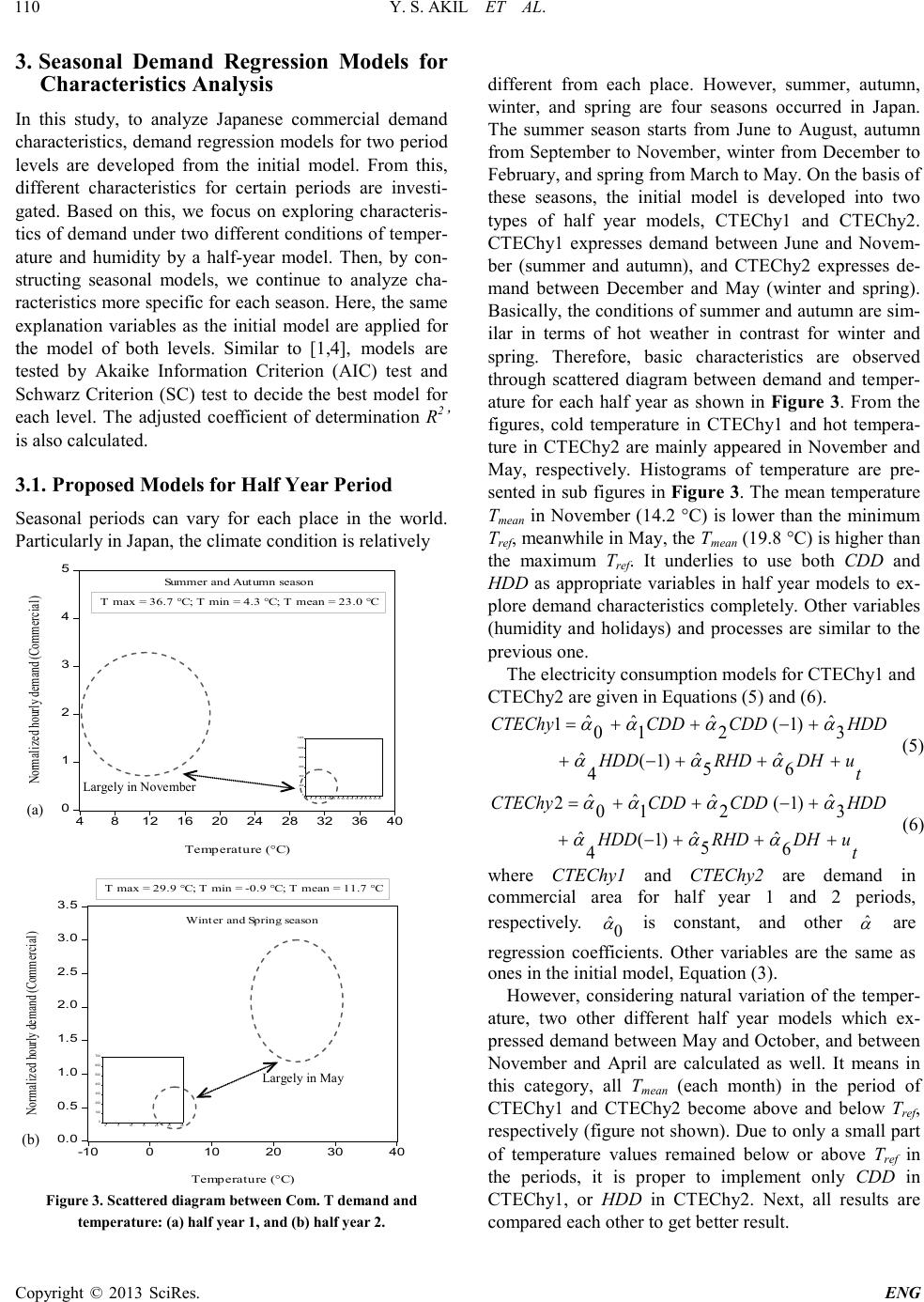 Y. S. AKIL ET AL. Copyright © 2013 SciRes. ENG 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 -10 010 20 30 40 Temperature (°C) Normalized hourly demand (Commercial) Winter and Spring season T max = 29.9 °C; T min = -0.9 °C; T mean = 11.7 °C 0 100 200 300 400 500 600 700 0510 15 20 25 30 (b) Largely in May 0 1 2 3 4 5 4812 16 20 24 28 32 36 40 Temperature (°C) Normalized hourly demand (Commercial) Summer and Autumn season T max = 36.7 °C; T min = 4.3 °C; T mean = 23.0 °C 0 200 400 600 800 1,000 1,200 468 10 12 14 16 18 20 22 24 26 28 30 32 34 36 Largely i n November 3. Seasonal Demand Regression Models for Characteristics Analysis In this study, to analyze Japanese commercial demand characteristics, demand regression models for two period levels are developed from the initial model. From this, different characteristics for certain periods are inves ti- gated. Based on this, we focus on exploring characteris- tics of dema nd under two d ifferent conditio ns of temper- ature and humidity by a half-year model. Then, by con- structing seasonal models, we continue to analyze cha- racteristics more specific for each season. Here, the same explanation variables as the initial model are applied for the model of both levels. Similar to [1,4], models are tested by Akaike Information Criterion (AIC) test and Schwarz Criterion (SC) test to decide the best model for each level. The adjusted coefficient of determination R2’ is also calculate d. 3.1. Proposed Mod e ls for Ha lf Year Period Seasonal periods can vary for each place in the world. Particularly in Japan, the climate condition is relatively Figure 3. Scat tered diagram between Com. T demand a nd temperature: (a ) half year 1, and (b) half year 2. different from each place. However, summer, autumn, winter, and spring are four seasons occurred in Japan. The summer season starts from June to August, autumn from September to November, winter from December to February, and spring fr om March to Ma y. On t he basis of these seasons, the initial model is developed into two types of half year models, CTEChy1 and CTEChy2. CTEChy1 expresses demand between June and Novem- ber (summer and autumn), and CTEChy2 expresses de- mand between December and May (winter and spring). Basically, the co nd itio ns of su mme r and aut umn ar e sim- ilar in terms of hot weather in contrast for winter and spring. Therefore, basic characteristics are observed through scattered diagram between demand and temper- ature for each half year as shown in Figure 3. Fro m the figures, cold temperature in CTEChy1 and hot tempera- ture in CTEChy2 are mainly appeared in November and May, respectively. Histograms of temperature are pre- sented in sub figures in F igure 3. The mean temperature Tmean in November (14.2 °C) is lower than the minimum Tref, mea n whi le i n May, the Tmean (19.8 °C) is higher than the maximum Tref. It underlies to use both CDD and HDD as appropriate variables in half year models to ex- plore demand characteristics completely. Other variables (humidity and holidays) and processes are similar to the previous one. The electricity consumption models for CTEChy1 and CTEChy2 are given in Equations (5) and (6). t uDHRHDHDD HDDCDDCDDCTEChy +++−+ +−++= 6 ˆ 5 ˆ )1( 4 ˆ 3 ˆ )1( 2 ˆ 1 ˆ 0 ˆ 1 ααα αααα (5) t uDHRHDHDD HDDCDDCDDCTEChy +++−+ +−++= 6 ˆ 5 ˆ )1( 4 ˆ 3 ˆ )1( 2 ˆ 1 ˆ 0 ˆ 2 ααα αααα (6) where CTEChy1 and CTEChy2 are demand in commercial area for half year 1 and 2 periods, respectively. is constant, and other are regression coefficients. Other variables are the same as ones in the initial mode l, Equation (3). However, considering natural variation of the temper- ature, two other different half year models which ex- presse d demand between May and October, and between November and April are calculated as well. It means in this category, all Tmean (each month) in the period of CTEChy1 and CTEChy2 become above and below Tref, resp ective ly (f igure not s hown) . Due to onl y a s mall pa rt of temperature values remained below or above Tref in the periods, it is proper to implement only CDD in CTEChy1, or HDD in CTEChy2. Next, all results are compared each other to get better result.  Y. S. AKIL ET AL. Copyright © 2013 SciRes. ENG -10 0 10 20 30 40 1 2 3 4 T maxT meanT min SM A WS Time period Temperature (°C) Sep - Nov Dec - Feb Tref lines (1.71) Notes: ( ) M ean de mand 3.2. Proposed Models for Seasonal Demand Models With regard to the eff ort to reveal dem and characteristics, the preceding models are developed according to the seasons. Four electricity consumption models, namely summer (CTECSM), autumn (CTECA), winter (CTECW), and spring model (CTECS) are composed. Based on the seasons, November and May are months in aut u mn and sp ring sea son, re spe ctive ly. The refo re, we use two temperature variables (CDD and HDD) to com- pose autumn and spring models (CTECA and CTECS). For other two models (CTECSM and CTECW), both in their periods contain a few temperature values below (Tmin = 13.4 °C) or above (Tmax = 20.8 °C) of Tref range. Howev e r, we consider only dominant temperature to compose CTECSM and CTECW models for simplifica- tion. The range of temperature for each season is shown in Figure 4. The regression equations for each seasonal model are defined in Equations (7)-(10). t uDH RHDCDDCDDCTECSM ++ +−++= 4 ˆ3 ˆ )1( 2 ˆ 1 ˆ 0 ˆ β ββββ (7) t uDHRHDHDD HDDCDDCDDCTECA +++−+ +−++= 6 ˆ 5 ˆ )1( 4 ˆ3 ˆ )1( 2 ˆ 1 ˆ 0 ˆ βββ ββββ (8) t uDH RHDHDDHDDCTECW ++ +−++= 4 ˆ3 ˆ )1( 2 ˆ 1 ˆ 0 ˆ β ββββ (9) t uDHRHDHDD HDDCDDCDDCTECS +++−+ +−++= 6 ˆ 5 ˆ )1( 4 ˆ3 ˆ )1( 2 ˆ 1 ˆ 0 ˆ βββ ββββ (10) where CTECSM, CTECA, CTECW, and CTECS show demand in summer, autumn, winter, and spring season, respectively. The is constant, and other values are Figure 4. Comparison of temperature limits for each season: SM = summer, A = autumn, W = winter, S = spring. regression coefficients. The other variables are the same as ones i n t he previo us mo d el , Equatio n (3). 4. Result and Analysis 4.1. Demand Char a ct erist ics with Al l Period The regression coefficients and results of the statistical tests for the initial model of commercial area is listed in Table 1. From tested Tre f (Tre f 1 = Tref2 = Tref ) in the model, 19 °C gives better result from the assessment by AIC test, SC test, and R2’. The results listed in Tables 1 is the results for Tre f = 19 °C. In this study, EViews 6 [8] is used to compute the model eq uations. As presented in Table 1, R2 and R2’ are almost 90%. It indicates that used variables can explain the commercial demand well. The application of 5% significance level for p-value gives that all explanation variables are significant. The value of 0 for Prob. (F-Statistics) indicates at least one of the applied variables influence the demand. Besi de s, Dur b in-Watson (D-W) statistic implies the initial model doe s not contain serial correlation because its value is around 2. To confirm the nonexistence of heteroskedasticity problem, corrected standard errors regression is performed [7]. The related adjusted standard errors are listed in Table 1 as well. Among coefficie nt values for meteoro logical variables, CDD (0.0410) has the highest influence to the demand, followed by HDD, CDD(-1), HDD(-1), and RHD. As temperature functions, the coefficient ratio of CDD to HDD (α1/α3) [9] is around 2.67. The comme rcial de mand can increase easier under hot temperature than under cold temperature. Likewise for influence of one hour previous temperature, CDD(-1) affects the demand around 4.03 times of HDD(-1). For humidity, it has the lowest influence to demand. As coefficient for dummy holidays α6 is ne gative, demand is lower in holida ys than in non-holidays. Note: R2 = 0.8988; R2’ = 0.8988; SE Reg. = 0.1814; D-W = 2. 1230; Prob. (F-Stat.) = 0.0000; AIC = -0.5752; SC = -0.5719 Expl. Variabl e All Period Demand Model CTEC Mo de l (Tref = 19 °C ) Coef. t-statistic (p-value) standard error 0 α 1.7456 81.93 0 0.0213 CDD 0.0410 30.88 0 0.0013 CDD(-1) 0.0125 13.61 0 0.0009 HDD 0.0153 24.08 0 0.0006 HDD(-1) 0.0031 5.44 0 0.0005 RHD 0.0011 11.96 0 9.7E-05 DH -0.1744 -60.58 0 0.0028 Table 1. Regression results for all period demand model.  Y. S. AKIL ET AL. Copyright © 2013 SciRes. ENG 10 20 30 40 50 60 70 80 90 100 123456 7 8 910 11 12 RHD min RHD mean RHD max Relative humidity (%) Jun Jul Aug Sep OctNov DecJan Feb Mar Apr May Month RHD mean 4.2. Demand Char a ct erist ics with Hal f Year Models Half year models started from May to October (CTEChy1) and from November to April (CTEChy2) are obtained. Naturally, as period of CTEChy1 is hot season, the tem- perature in CTEChy1 is higher than CTEChy2. Moreover, all monthl y a verage va lues o f humidit y (RHD mean) i n the period of CTEChy1 tend to higher than in the period of CTE Chy2 as shown in F ig ur e 5. The best results for half year models which are specified with second order autoregressive error ter m are presented in Tables 2 and 3. In Table 2, where 19 °C and 16 °C are optimum Tref va lue s for CDD in CTECh y1 , a nd HDD in CTEChy2 model, respectively. T he statistical Figure 5. Variation of humidity values for each month from June 2000 to May 2007 Table 2. Regressi on coeffi cients of the half y ear models. results in Table 3 and Table 2 show both models validated well. B y separating the perio d, the value of R2’ increases slightly in CTEChy1 (90.88%) and decreases in CTEChy2 (85.55%) when we compared with R2’ val ue of CTEC model (89.88%). CTEChy1 has higher degree of fitne ss t ha n CT E Ch y2 model. For constant values , it is obtained larger in CTEChy2 (1.8137) than in CTEChy1 (1.6260). The constant value is associated with base demand. Among meteorological variables in CTEChy1 and CTEChy2 models as in Table 2, CDD (0.0468) and HDD (0.0178) have the largest effect to the demand, respectively. However, comparing these coefficient values (CDD in CTEChy1, and HDD in CTEChy2), the demand responses higher in hot temperature than in cold temperature. Concerning humi dity, this variable gives the lowest influence, and affects the demand only in CTEChy1 period (high humidity). The elimination of non-significance variable RHD in CTEChy2 is proper as it gives almost the same r esults. T he dummy variable DH shows decrease of the commercial demand in holidays, but in different amount for both half year models. 4.3. Demand Characteristics with Seasonal Models Tables 4 and 5 present best regression results with opti- mum Tref for each seasonal model. Optimum Tref is 19 °C for summer and autumn models, meanwhile 16 °C for other two models. The Tref value tends to high under hot seasons and vice versa. From the results, the value R2’ ranges between 81.34% and 90.19%. The models under hot seasons (CTECSM and CTECA) have higher R2’ values than others under cold seasons (CTECW and CTE CS ). The hig hest R2’ is in summer, and the lowest is in winter. However, with R2’values exceed 80% and three of them above 86%, all models have quite good fitness degree. Next, among implemented var ia bles in the seasonal models, CDD(-1) and HDD(-1) in spring (CTECS) are not significant at 5% significance le vel. As spring is not so hot or so cold (comfortable season), it may related to the non-significance of the one hour pre- vious temperature (CDD(-1) and HDD(-1)) to demand. For simplification, both CDD(-1) and HDD(-1) in CTECS model can be eliminated without influence on regr ession r esults. Expl. Variable Half Y ear Dem and Model CTEChy1 (Tref = 19 °C) CTEChy2 (Tref = 16 °C) Coef. (p-value) Coef. (p-value) 1.6260 0 1.8137 0 (48.26) 0.0336* (74.35) 0.0243* CDD 0.0468 0 (31.75) 0.0014* CDD(-1) 0.0110 0 (11.84) 0.0009* HDD 0.0178 0 (24.01) 0.0007* HDD(-1) 0.0030 0 (4.61) 0.0006* RHD 0.0030 0 8.00E-05 0.4484 (16.92) 0.0001* (0.75) 0.0001* DH -0.1870 0 -0.1562 0 (-43.16) 0.0043* (-44.29) 0.0035* Notes: CTEChy1 = from May to October; CTEChy2 = from November to April; () t -statistic; *adjs. s tanda rd e rro r; _not significant related to its var iab le Table 3. Regressi on statistics of the half y ear models. R2 R2’ D-W AIC SC CTEChy1 0.9089 0.9088 0.1978 2.1343 -0.4024 -0.3982 CTEChy2 0.8556 0.8555 0.1524 2.0946 -0.9231 -0.9178 N ote : Prob. (F-Stat.) both C TEChy1 a nd CTEC hy2 = 0. 0000; Without RHD in CTEChy2 mode l, R2’ = 85.55% 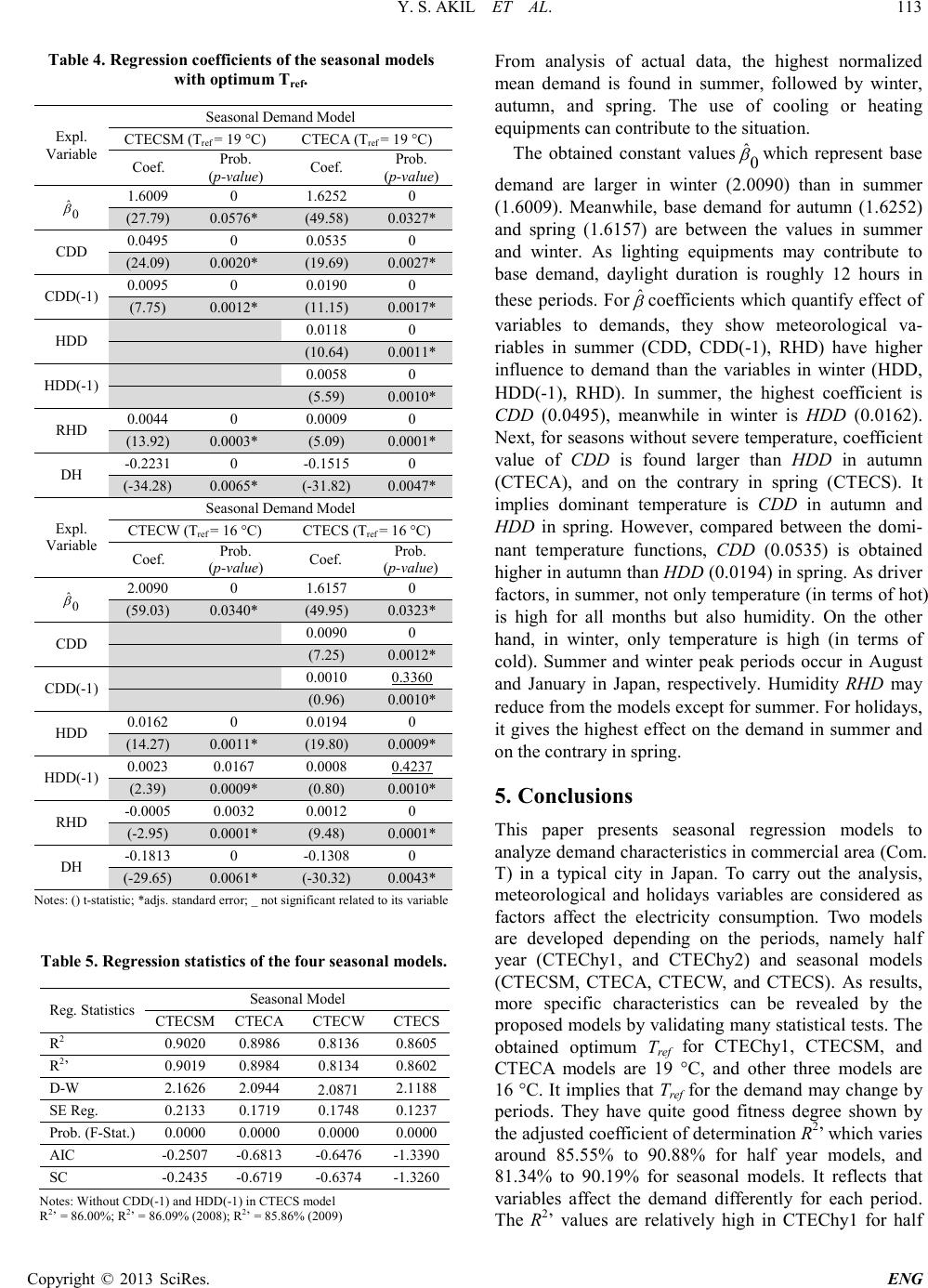 Y. S. AKIL ET AL. Copyright © 2013 SciRes. ENG Table 4. Regressi on coeffi cients of the seasonal models with optimum Tref . From analysis of actual data, the highest normalized mean demand is found in summer, followed by winter, autumn, and spring. The use of cooling or heating equipments can contribute to the sit uation. The obtained constant values which represent base demand are larger in winter (2.0090) than in summer (1.6009). Meanwhile, base demand for autumn (1.6252) and spring (1.6157) are between the values in summer and winter. As lighting equipments may contribute to base demand, daylight duration is roughly 12 hours in these periods. For coefficients which quantify effect of variables to demands, they show meteorological va- riables in summer (CDD, CDD(-1), RHD) have higher influence to demand than the variables in winter (HDD, HDD(-1), RHD). In summer, the highest coefficient is CDD (0.0495), meanwhile in winter is HDD (0.0162). Next, for sea sons withou t severe temperature, coefficient value of CDD is found larger than HDD in autumn (CTECA), and on the contrary in spring (CTECS). It implies dominant temperature is CDD in autu mn and HDD in spring. However, compared between the domi- nant temperature functions, CDD (0.0535) is obtained higher i n a ut u mn t ha n HD D (0.0194) in spring. As drive r factors, in su mmer, n ot only temperature (in ter ms of hot) is high for all months but also humidity. On the other hand, in winter, only temperature is high (in terms of cold). Summer and winter peak periods occur in August and January in Japan, respectively. Humidity RHD may reduce from the models except for summer. For holidays, it gives the highest effect on the demand in summer and on the contrary in spring. 5. Conclusions This paper presents seasonal regression models to analyze demand characteristics in com mercial area (Com. T) in a typical city in Japan. To carry out the analysis, meteorological and holidays variables are considered as factors affect the electricity consumption. Two models are developed depending on the periods, namely half year (CTEChy1, and CTEChy2) and seasonal models (CTECSM, CTECA, CTECW, and CTECS). As results, more specific characteristics can be revealed by the proposed models by validatin g many statistica l tests. The obtained optimum Tref for CTEChy1, CTECSM, and CTECA models are 19 °C, and other three models are 16 °C. I t implies that Tref for the de mand may change b y periods. They have quite good fitness degree shown by the adjusted coefficient of determination R2’ which varies around 85.55% to 90.88% for half year models, and 81.34% to 90.19% for seasonal models. It reflects that variables affect the demand differently for each period. The R2’ values are relatively high in CTEChy1 for half Expl. Variable Seasonal Demand Model CTECSM (Tref = 19 °C) CTECA (Tref = 19 °C) Coef. Coef. 0 ˆ β 1.6009 0 1.6252 0 (27.79) 0.0576* (49.58) 0.0327* CDD 0.0495 0 0.0535 0 (24.09) 0.0020* (19.69) 0.0027* CDD(-1) 0.0095 0 0.0190 0 (7.75) 0.0012* (11.15) 0.0017* HDD 0.0118 0 (10.64) 0.0011* HDD(-1) 0.0058 0 (5.59) 0.0010* RHD 0.0044 0 0.0009 0 (13.92) 0.0003* (5.09) 0.0001* DH -0.2231 0 -0.1515 0 (-34.28) 0.0065* (-31.82) 0.0047* Expl. Variable Seasonal Demand Model CTECW (Tref = 16 °C) CTECS (Tref = 16 °C) Coef. (p-value) Co ef . (p-value) 0 ˆ β 2.0090 0 1.6157 0 (59.03) 0.0340* (49.95) 0.0323* CDD 0.0090 0 (7.25) 0.0012* CDD(-1) 0.0010 0.3360 (0.96) 0.0010* HDD 0.0162 0 0.0194 0 (14.27) 0.0011* (19.80) 0.0009* HDD(-1) 0.0023 0.0167 0.0008 0.4237 (2.39) 0.0009* (0.80) 0.0010* RHD -0.0005 0.0032 0.0012 0 (-2.95) 0.0001* (9.48) 0.0001* DH -0.1813 0 -0.1308 0 (-29.65) 0.0061* (-30.32) 0.0043* Note s: () t-st a t is tic ; *adjs . s ta nda rd error; _ not significant related to its varia ble Reg. Statistics Seasonal Model CTECSM CTECA CTECW CTECS R2 0.9020 0.8986 0.8136 0.8605 R2’ 0.9019 0.8984 0.8134 0.8602 D-W 2.1626 2.0944 2.0871 2.1188 SE R eg . 0.2133 0.1719 0.1748 0.1237 Prob. (F-Stat.) 0.0000 0.0000 0.0000 0.0000 AIC -0.2507 -0.6813 -0.6476 -1.3390 SC -0.2435 -0.6719 -0.6374 -1.3260 Notes: Without CDD(-1) and HDD(-1) in CTEC S mode l R2’ = 86.00%; R2’ = 86.09% (2008); R2’ = 85.86% (2009) Table 5. Regression st ati stics of the four seasonal models.  Y. S. AKIL ET AL. Copyright © 2013 SciRes. ENG year model, and in CTECSM (summer) and CTECA (autumn) for seasonal models. Implemented variables can explain commercial demand o ptimally in ho t weather rather than in cold weather. The base demand is relatively higher in the cold than in hot season. Among meteorological variables, CDD and HDD are the most significant variables. For non-significance variables, elimination of them results in simplified models which may reduce computation burden. Next, in holidays, demand decreses in a ll period s b ut in difference amount. The presented results can give more insight especially when demand characteristics in seasonal levels are required. It is usefull in quantifying influence of variables on demand at certain area or period, and in understanding demand situati on more detail. REFERENCES [1] A. Pardo, V. Meneu and E. Valor, “Temperature and Seasonality Influences on Spanish Electricity Load,” Energy E conomics, Vol. 24, 2002, pp. 55-70. doi: 10.1016/S0140-9883(01)00082-2 [2] J. C. Lam, “Climatic and Economic Influences on Residential Electricity Consumption,” Energy Convers. Mgmt, Vol. 39, No. 7, 1998 , p p. 623-629. doi: 10.1016/S0196-8904(97)10008-5 [3] K. Wangpattarapong, S. Maneewan, N. Ketjoy and W. Rakwichian, “The Impacts of Climatic and Economic Factors on Residential Electricity Consumption of Bang- kok Metropolis,” Energy and Buildings, Vol. 40, 2008, pp. 1419 -1425. doi: 10.1016/j.enbuild.2008.01.006 [4] S. Mirasgedis, Y. Sarafidis, E. Georgopoulou, D. P. Lalas, M. Moschovits, F. Karagiannis and D. Papakonstanti- nou, “Models for Mid-Term Electricity Demand Forecasting Incorporating Weather Influences,” Energy, Vol. 31, 20 06 , pp. 208-227. doi: 10.1016/j.energy.2005.02.016 [5] Japan Meteorological Agency (JMA). http://www.jma.go.jp/jma/indexe.ht ml [6] B. E. Psiloglou, C. Giannakopoulos, S. Majithia and M. Petrakis, “Factors Affecting Electricity Demand in Athens, Greece and London, UK: A Comparative Assessment,” Energy, Vol. 34, 20 09, pp. 1855-1863. doi: 10.1016/j.energy.2009.07.033 [7] R. S tartz, “EViews Illustrated for Version 6,” 1st Edition, Quantitative Micro Software, LLC, 2007. [8] EViews. http://www.eviews.com [9] D. J. Sailor and J. R. Muñoz, “Sensitivity of Electricity and Natural Gas Consumption to Climate in the U.S.A.–Methodology and Results for Eight States,” Energy, Vol. 22, No. 10, 1997, pp. 9 87-998. doi: 10.1016/S0360-5442(97)00034-0
|