Engineering, 2013, 5, 69-74
doi:10.4236/eng.2013.51b013 Published Online January 2013 (http://www.SciRP.org/journal/eng)
Numerical Study of a Con f ined Axisymmet ri c Jet
Impingement Heat Transfer with Nanofluids
Jun-Bo Huang, Jiin-Yuh Jang
Department of Mechanical Engineering, National Cheng-Kung University
Received 2013
ABSTRACT
A nume rical si mulatio n on conf ined imp inging ci rcular jet worki ng with a mixture of wate r and Al2O3 nanop articles is
investigated. The flow is turbulent and a constant heat flux is applied on the heated plate. A two-phase mixture model
approach has been adopted. Different nozzle-to-plate distan ce, nanoparticle volume concentrations and Reynolds num-
ber have been considered to study the thermal performances of the system in terms of local, average and stagnation
point Nusselt number. T he local Nusselt n umber p r ofi les s how t ha t t he hi g hest va l ue s wit hi n the s tag na tion p o int re gion,
and the lowest at the end of the heated plate. It is observed that the average Nusselt number increases for increasing
nanoparticle concentrations, moreover, the highest values are observed for H/D = 5, and a maximum increase of 10% is
obtained at a concentration equal to 5%.
Keywords: Nanofluid; Confined J et; Turbulent Flow
1. Introduction
Among the numerous approaches enhancing heat transfer
rate, j et impingement is o ne of the most powerful cooling
solutions for high heat flux removal by impinging fluid
on a heater surface. Applications of impinging jets include
drying of textiles and films, cooling of gas turbine,
material processing and electronic cooling. Many studies
considering jet impingements with liquids have been
carried out due to their high heat transfer performances.
Comparison between the cooling performances of water
and air impingement reveals that the thermophysical
prop erties of working fluid will greatl y affect the cooling
features.
In the e xistin g invest igation s, the t hermal co nducti vity
of some traditional natural and organic working fluids
such as water or ethylene glycol may not meet the re-
quirement of high-heat-flux removal. To meet the needs
of enhanced heat transfer, an innovative category of heat
transfer fluid, nanofluid, has been proposed with devel-
opment of nanomaterial technology. Nanofluid, a mix-
ture of nanoparticles with average particle size smaller
than 100nm suspended in base fluid such as water or
ethylene glycol, has drawn much attention due to the
potential for high rate of heat transfer with little penalty
in pressure drop.
Impi nging je ts with o r witho ut confi nement ha ve bee n
widely investigated over the past several decades. Con-
finement has significant effects on the flow field of the
jet, as well as on the heat transfer rates and distribution.
The existence of the secondary peak of local Nusselt
number was found, which is believed to be due to the
laminar -turbulent transition of the flow. In recent years,
many researchers have carried out numerical investiga-
tions of impinging jet heat transfer with different work-
ing fluids and under various boundary conditions. For
example, Gherasim et al. [1] highlighted the limitations
in the use of Al2O3 /water nan ofluid in a rad ial flo w con-
figura ti o n d ue to the significant increase in the associated
pumping power. Also, Yang and Lai presented numerical
results on confined jets with constant [2] and tempera-
ture-dependent [3] properties. Results confirmed the
Nusselt number increases with the increase of Reynolds
number and nanoparticle volume fraction and the in-
crease in pressure drop. Furthermore, temperature-de-
pendent thermophysical properties of nanofluids were
found to have a marked bearing on the simulation re-
sults.Manca et al. [4] numerically investigated the con-
fining effects on impinging slot jets in the turbulent re-
gime, such as for Reynolds numbers, ranging from 5000
to 20000. They adopted the single-phase approach in
order to describe the Al2O3/water nanofluid behaviour
for particle concentrations up to 5%. A significant en-
hancement in terms of convective heat transfer coeffi-
cients was evaluated for high particle volume concentra-
tions as well as an increase of required pumping power.
To our knowledge, there exists relatively sparse nu-
merical data regarding the heat transfer performance of
nanofluids turbulent flow under the geometrical configu-

J.-B. HUANG, J.-Y. JANG
70
ration of a confined impinging jet. In the present paper,
Al2O3-water nanofluids are introduced into confined sin-
gle ci rcula r je t impinge ment coo ling s ystem a s the work-
ing fluid. The objective of this work is to numerically
investigate the impingement heat transfer features of the
nanofluids. The effects of the nanoparticle concentration,
Reynolds number and nozzle-to-plate distance on the
heat transfer and flow performances of the nanfluids for
the jet impingement are discussed. The results are ex-
pected to be valuable toward the design of cooling sys-
tem for e ngineering ap plications.
2. Geometrical Configuration
An axisymmetric turbulent confined jet impinging on a
flat plate with constant heat flux has been analyzed nu-
merically. A geometrical configuration used in the analy-
sis is shown in Figure 1. Because of axisymmetric, si-
mulation of only a half-doma in is adequate for com-
plete characterization of the flow. The jet orifice diame-
ter D is 2mm. The geo metrical c onfiguration has a radius
R equal to 16 mm and the nozzle-to-plate distance H/D
ranging from 1 to 5.
3. Mathmatical Method
3.1. Mixture Model
For incompressible steady flow, the continuity equation
for the mixtur e is:
0=








⋅∇
→
m
m
v ρ
(1)
The momentum equation for the mixture can be ex-
pressed as:







+⋅∇+
⋅∇+−∇=








⋅∇
→→→→
→→→
sdrsdr
ss
pdrpdr
pp
mmm
m
vvvv
pvv
,,,,
ραρα
τρ
(2)
( )
→→→→ −







∇+∇+= Ikvv mm
T
mm
mtm
m
ρµµτ
3
2
,
(3)
The energy equation for the mixt ure is:
( ) TTvcTvc
meff
s
spss
p
pppp
∇⋅∇=







+⋅∇
→→
,,,
λραρα
(4)
D
H
Jet
Confined wallConfined wall
Impingement Surface
Pressure Outletyr
Figure 1. Sketch of the geometrical model.
m
ρ
is the mixture density defined as :
ssppm
ραραρ +=
(5)
m
v
→
is the mas s-averaged mixture velocity :
m
s
ss
p
pp
m
vv
v
ρ
ραρα
→→
→
+
=
(6)
p
α
and
s
α
are the volume fractions of the primary
and the secondary phases, respectively.
p
ρ
and
s
ρ
are
the densitie s of t he primary and the secondary phases, re-
spectively. ,
pp
c and ,ps c are the specific heat of the
pri- mary and the secondary phases, respectively.
,eff m
λ
is the effective thermal conductivity.
The viscosity of the mi xtur e
m
µ
is defined as:
ssppm
µαµαµ +=
(7)
where
p
µ
and
s
µ
are the viscosities of the primary
phase and the secondary phase, respectively. The drift
velocity for the secondary phase
,dr s
v
→
is defined as the
velocity of the dispersed phase relative to that of the
mixtur e ve lo city:
mssdr
vvv
→→→
−=
,
(8)
The slip of the secondary dispersed phase relative to
continuous phase is calculated by balancing the drag and
body forces resulting from density differences. The rela-
tive velocity
sp
v
→
is defined as the velocit y of the second-
dary phase relative to the pri mary phase velocity.
pssp
vvv
→→→
−=
(9)
The dr ift velocity is related to the relati ve velo c ity:
sp
m
ss
spsdr vvv →→→ −=
ρ
ρα
,
(10)
The relative velocity is calculated by:
( )
→→
−
=a
f
d
v
Dp
sms
sp
µ
ρρ
18
2
(11)
where s d is the diameter of the particles of secondary
phase and
a
→
is the secondary phase particle accelera-
tion. T he drag functio n
D
f
is given by:
24
Re
D
D
C
f=
(12)
There are several correlations that fit the drag coeffi-
cient as a function of Reynolds number available in the
literature. The general form used in this study is given
by:
2
32
1Re
Re
aa
aCD++=
(13)
where a1, a2 and a3 are sets of constants that apply over
various range of Reynolds number.

J.-B. HUANG, J.-Y. JANG
71
The acceleration
a
→
is given by:
t
v
vvga
m
mm
∂
∂
−







∇⋅−=
→
→→→→
(14)
From the continuity equation for the secondary phase,
the volume fraction equation for the secondary phase is:








−∇=








∇
→→
sdr
ss
m
ss
vv
,
ραρα
(15)
3.2. Turbulence Modeling
Previous studies have shown that the heat transfer simu-
lation of turbulent confined jet flow configuration is
quite co mplex. A suitable turb ulence model is re quired to
predict the flow and thermal structure with reasonable
accuracy. This is required to minimize the error associ-
ated with turbulence modeling and enables the investiga-
tion of the mixture model. A comparison between the
results obtained by using different turbulence models has
shown that a k-ω based shear stress transport (SST)
model developed by Menter [8] is the appropriate model
to determine the local wall Nusselt number for this kind
of flow co n figura tion. The k-ω SST model include the
addition of a cross-diffusio n ter m in the ω equat ion a nd a
blending function to ensure that the model equations be-
have appropriately in both the near-wall and far-field
zones. It has been shown to be quite adequate for appli-
cations with separating flows. This turbulence model is
used in the present work. The transport equations for
SST
k ω −
are:
kk
k
t
m
m
YGkkv−+







∇







+∇=








⋅∇
→
σ
µ
µρ
(16)
ωωω
ω
ω
σ
µ
µωρ DYGv
t
m
m
+−+







∇







+∇=








⋅∇
→
(17)
In Eqs. (16) and (17), Gk represents the generation of
the turbulent kinetic energy k, due to mean velocity gra-
dients, and Gω represents the generation of the specific
dissipation rate ω. Yk and Yω represents the dissipa tion of
k and ω due to turbulence. Dω is a cr oss-diffusion term .
3.3. Boundary Conditions
The bo undary conditions are expressed as follows:
Inlet section: Uniform temperature equal to 300K and
different uniform velocities, corresponding to Reynolds
number ranging from 5000 to 30000 are considered.
Furthermore, the inlet turbulence intensit y value is set to
2%.
Outlet section: pressure outlet boundary condition is
specified.
Botto m wall: T he no-slip boundary condition is imposed
on the target plate that i s ke pt at const ant hea t fl ux o f 5 x
105W/m2.
Upper wall: The no-slip boundary condition is imposed
on the confinement surface that is considered to be an
adiabatic wall.
The axis-symmetric boundary condition is applied
along the line of axis-symme tr ic. The working fluid is
water or a mixture of water and Al2O3 nanoparticles at
different volume fractions equal to 1, 3 and 5%.
3.4. Physical Properties of Nanof luids
The following equations are used to evaluate the effect-
tive prope rties of the nano fluid.
Density:
( )
pfnf
φρρφρ +−= 1
(18)
Specific heat:
( )
pppfpfnfpnf
ccc
,,,
1 φρρφρ +−=
(19)
Viscosity:
( )
fnf
µφφµ 13.7123
2
++=
(20)
This was presented by the Maiga et al. [9] for water-
Al2O3 nanofluid based on available experimental results
in the literature.
Thermal conductivity:
( )
fnf
kk 172.297.4
2
++= φφ
(21)
3.5. Dimens ionl ess Para m eter s
The dimensionless parameters considered here are:
µ
ρ VD
=Re
(22)
k
D
TT
q
k
hD
Nu
fs −
== "
(23)
The local Nusselt number distribution is averaged to
obtain an average Nusselt number. The average Nusselt
number is defined as
∫⋅⋅==
R
o
drrNu
R
k
Dh
Nu
2
2
(24)
3.6. Numerical Procedure
The computational fluid dynamic code FLUENT was
employed to solve the present problem. The governing
equations of continuity, momentum and energy were
solve d by the fi ni te vo l u me me tho d . A QUICK scheme is
chosen for momentum and energy equations. The SIM-
PLE algorithm was chosen as scheme to couple pressure
and velocity. The discretization grid is finer near the wall
where the velocity and temperature gradients are signifi-

J.-B. HUANG, J.-Y. JANG
72
cant. The convergence criteria of 10-5 for the resid uals o f
the velocity components and of 10-6 for the residuals of
the energy are specified.
4. Results and Discussion
The local Nusselt number distributions for H/D= 2 are
sho wn in F ig ure 2. T he local Nusselt numbers at the first
peaks (Nu1st) are approximately 7% - 10% higher than
the stagnation point values (Nu0) for all the cases
considered in the paper. The first peak values of the 8%
nanofluid jet are about 5% - 6% higher than the
stagnation point values of the water jet. However, the
local Nusselt numbers at the second peaks (Nu2nd) are
approximately 2% - 14% less than the stagnation point
values. The ratio of Nu2nd/Nu1st is weakly dependent on
the jet Reynolds number. These results indicate that the
heat transfer mechanism between these two peaks is
nearly independent of the jet Reynolds number. The first
peaks in local Nusselt number distributions correspond-
ing to the maximum heat transfer rates occur at r/D~0.5
of the orifice noz zles. T he first p eak is stron gly attr ibuted
to the high turbulence intensity at the nozzle edge. The
secondary peaks occur in the range of 1.4<r/D<1.9 fo r a l l
nozzle configurations and Reynolds numbers tested.
The local heat transfer distributions for the nozzle-
to-plate spacing of H/D = 5 are shown in F igure 3. The
local Nusselt numbers decrease monotonically and do not
show the secondary maxima at all. For all the cases con-
ducted in the paper, the local heat transfer distributions
show nearly similar shapes in the wall jet region. In the
stag natio n regio n, the 5% nanofluid jets have highe r hea t
transfer rates than the other jets. The stagnation point
r / D
Nu
01234
100
150
200
250
Pure Water
1% Nanofluid
3% Nanofluid
5% Nanofluid
H/D=2, Re=20000
Figure 2. Local Nusselt number distribution at the nozzle-
to-plate s pacing of H/D=2.
r / D
Nu
01234
100
150
200
250
Pure Water
1% Nanofluid
3% Nanofluid
5% Nanofluid
H/D=5, Re=20000
Figure 3. Local Nusselt number distribution at the nozzle-
to-plate s pacing of H/D=5.
Re
Nuo
10000 20000 30000
100
150
200
250
300 Pure Water
Nanofluid 1%
Nanofluid 3%
Nanofluid 5%
H/D=2
Figure 4. Various of stagnation point Nusse lt numbers with
Reynolds number at H/D=2.
Nusselt numbers of the 5% nanofluid jet are approx-
imately 7-9% higher than those of the water jet. Fur-
the rmore, in the transition and wall jet regions, the local
heat transfer rates of the nanofluid jet with different vo-
lume fraction of nanoparticles are higher than the pure
water jet. For high H/D values, local Nusselt number
decreases more slowly than high H/W r atios.
The effects of volume fraction of nanoparticles on the
stagnation point heat transfer are shown in Figure 4 and
Figure 5 as functio n o f je t Re ynold s n umbe r. I t is sho wn
how the variation of nanofluid concentration affects the
heat transfer. The Reynolds number dependency of the
5% nanofluid jet is larger than that of the water jet at
H/D = 2. The effect of volume fraction of nanoparticles
on the stagnation point heat transfer is more sensible at
shorter nozzle-to-plate spacing. The present Nu0 data of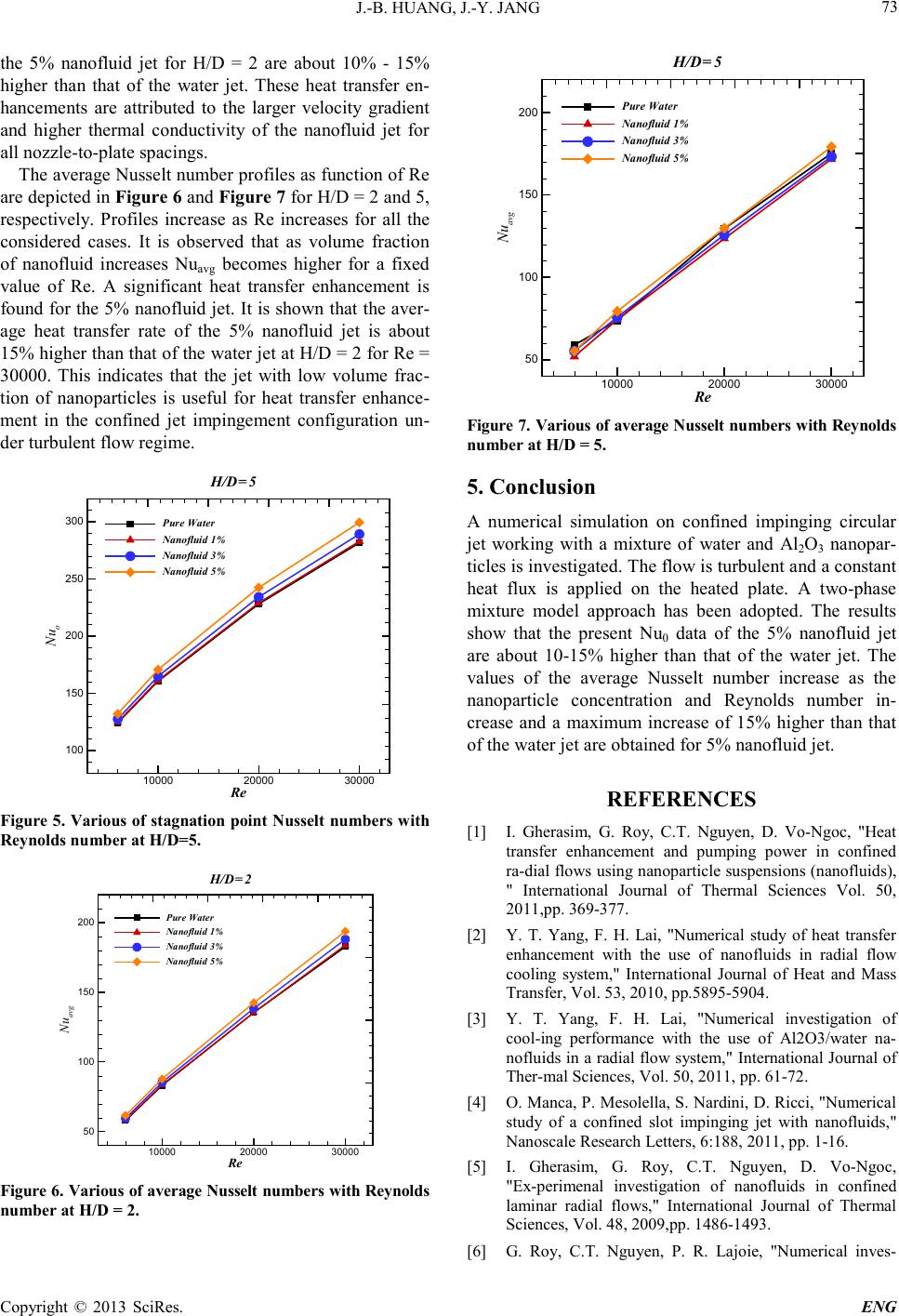

J.-B. HUANG, J.-Y. JANG
73
the 5% nanofluid jet for H/D = 2 are about 10% - 15%
higher than that of the water jet. These heat transfer en-
hancements are attributed to the larger velocity gradient
and higher thermal conductivity of the nanofluid jet for
all nozzle-to-plate spacings.
The average Nusselt number profiles as function of Re
are depicted in Figure 6 and Figure 7 for H/D = 2 a nd 5,
respectively. Profiles increase as Re increases for all the
considered cases. It is observed that as volume fraction
of nanofluid increases Nuavg becomes higher for a fixed
value of Re. A significant heat transfer enhancement is
found for the 5% nanofluid jet. It is shown that t he aver-
age heat transfer rate of the 5% nanofluid jet is about
15% higher than that o f the water je t at H/D = 2 for Re =
30000. This indicates that the jet with low volume frac-
tion of nanoparticles is useful for heat transfer enhance-
ment in the confined jet impingement configuration un-
der turbulent flow re gime.
Re
Nu
o
10000 20000 30000
100
150
200
250
300 Pure Water
Nanofluid 1%
Nanofluid 3%
Nanofluid 5%
H/D=5
Figure 5. Various of stagnati on point N usselt numbers w ith
Reynolds number at H/D=5.
Re
Nu
avg
10000 20000 30000
50
100
150
200 Pure Water
Nanofluid 1%
Nanofluid 3%
Nanofluid 5%
H/D=2
Figure 6. Various of aver age Nusselt nu mbe rs with Rey nolds
number at H/ D = 2.
Re
Nu
avg
10000 20000 30000
50
100
150
200 Pure Water
Nanofluid 1%
Nanofluid 3%
Nanofluid 5%
H/D=5
Figure 7. Various of a verage N usselt numbers w ith Rey nolds
number at H/ D = 5.
5. Conclusion
A numerical simulation on confined impinging circular
jet working with a mixture of water and Al2O3 nanopar-
ticles is investi gated. T he flow is turbule nt and a constant
heat flux is applied on the heated plate. A two-phase
mixture model approach has been adopted. The results
show that the present Nu0 data of the 5% nanofluid jet
are about 10-15% higher than that of the water jet. The
values of the average Nusselt number increase as the
nanoparticle concentration and Reynolds number in-
crease and a maximum increase of 15% higher than that
of the water jet are obtained for 5% nanofluid jet.
REFERENCES
[1] I. Gherasim, G. Roy, C.T. Nguyen, D. Vo-Ngoc, "Heat
transfer enhancement and pumping power in confined
ra-dial flows using nanoparticle suspensions (nanofluids),
" International Journal of Thermal Sciences Vol. 50,
2011,pp. 369-377.
[2] Y. T. Yang, F. H. Lai, "Numerical study of heat transfer
enhancement with the use of nanofluids in radial flow
cooling system," International Journal of Heat and Mass
Tra nsfer, Vol. 53 , 2010, pp.5 895-5904.
[3] Y. T. Yang, F. H. Lai, "Numerical investigation of
cool-ing performance with the use of Al2O3/water na-
nofluids in a radial flow system," International Journal of
Ther-mal Sciences, Vol. 50, 2011, p p. 61-72.
[4] O. M anca, P. Meso lella, S. Nardini, D. Ricci, "Numerical
study of a confined slot impinging jet with nanofluids,"
Nanoscale Research Letters, 6:188, 2011 , pp. 1-16.
[5] I. Gherasim, G. Roy, C.T. Nguyen, D. Vo-Ngoc,
"Ex-perimenal investigation of nanofluids in confined
laminar radial flows," International Journal of Thermal
Scie nc e s , Vol. 48, 2009,p p. 1486-1493.
[6] G. Roy, C.T. Nguyen, P. R. Lajoie, "Numerical inves-

J.-B. HUANG, J.-Y. JANG
74
ti-gation of laminar flow and heat transfer in a radial flow
cooling system with the use of nanofluids," Superlattices
and Microstructures, Vol. 35, 2004, pp. 497-511.
[7] G. Roy, I. Gherasim, F. Nadeau, G. Poitras, C. T. Nguyen,
“Heat transfer performance and hydrodynamic behavior
of turbulent nanofluid radial flows,” International
Jour-nal of Thermal Sciences, Vol. 58, 2012,pp. 120-129.
[8] F. Menter, Two-equation eddy-viscosity turbulence mod-
els for engineering applications, AIAA J., 32 (8), 1994,
pp. 1598 -1605.
[9] S.E.B. Maiga, N. Cong Tam, N. Galanis, G. Roy, T. Mar e,
M. Coqueux, “Heat transfer enhancement in turbulent
tube flow using Al2O3 nanoparticle suspension,” In-
ter-national Journal of Numerical Methods Heat Fluid
Flow, Vol. 16, 2006, pp. 275-292.
[10] S.J. Palm, G. Roy, C.T. Nguyen, “Heat transfer
en-hancement with the use of nanofluids in radial flow
cool-ing systems considering temperature dependent
properties,” Applied Thermal Engineering, Vol. 26, 2006,
pp. 2209 -2218.
[11] M. Manninen, V. Taivassalo, S. Kallio, On the Mixture
Model for Multiphase Flow, VTT Publica-tions 288,
Technical Research Centr e of Finlan d, 1996.