New Approach to Approximate Circular Arc by
Quartic Bezier Curve
Azhar Ahmad1, Rohaidah Masri,
Nor’ashiqin Mohd Idrus
Department of Mathematics
Universiti Pendidikan Sultan Idris
Tanjung Malim, Perak, Malaysia
1
Jamaluddin M. Ali
School of Mathematical Science
Universiti Sains Malaysia
Penang, Malaysia
Abstract—This paper presents a result of approximation an arc circles by using a quartic Bezier curve. Based on the
barycentric coordinates of two and three combination of control points, the interior control points are determined by forcing the
curvature at median point as similar as the given curvature at end points. Hausdorff distance is used to investigate the order of
accuracy compare to the actual arc circles through central angle of 0 TS d. We found that the optimal approximation order is
eight which is somewhat similar to preceding methods in the literatures.
Keywords- arc circle, barycentric coordinate, Hausdorff distance, quartic Bezier
1. Introduction
Parametric representations of curves and surfaces are
essential to the field of Computer Aided Geometric Design
(CAGD). Representing of an arc circles using parametric
curves is one of an important study in related to design conic
sections in geometric modeling. The important of arc circles in
geometric modeling are undeniable, along with the used of the
others primitive elements, such as a straight line, conic curves
and spiral. Arc circles are widely used in CAD/CAM and can
be found in industrial as well as in product manufacture; the
aircraft and the automobile industries where surfaces are
frequently constructed from curves involving circular arcs
using lofting or skinning technique [4]. Furthermore it is used
in solving communication problem between CAD/CAM
systems when working with curve representations in different
data formats [8]. Generally, these significant uses of
parametric polynomial curve are concentrated on the
aesthetical and functional purposes. Since NURBS form is the
standard form in most of geometric software systems so the
used of the curve that based on parametric polynomial
representation became more important.
A considerable amount of work has been done on
approximating circular arc by polynomial curves. We consider
that most of the previous work related to the used of the low
degrees of Bezier curve modeling. Although a circle arc can
be exactly represented by rational parametric curve of low
degree, such the rational quadratic Bezier, some CAD/CAM
systems require a polynomial representation of circular
segments. Also, some important algorithms, such as lofting
and blending cannot be directly applied to rational curves [10].
Previous work showed that we can only representing an arc
circle by polynomials curve with a small acceptable tolerance.
The cubic approximation was proposed by de Boor et al. [2]
and Dokken et al. [3]. Goldapp [5] presented the best k
G
cubic approximations for 0,1, 2k , whose approximation
orders are six. Ahn and Kim [1] gave the quartic 3
G
approximation to arc of angle 0 TS d. Their approach has
the optimal approximation of order eight. And they also find
the quintic 4 G approximation with order ten. Kim and Ahn [7]
presented the quartic Bezier approximations of circular arcs
with approximation of order eight by using subdivision
scheme with equi-distance of the circular arc. The
approximation proposed by them has a smaller error than other
previous results. By using quintic, Fang [4] presented a
scheme with different boundary conditions that yields
approximation curves with k
G, 2,3,4k continuities at the
circular arc’s ends.
In our method, we consider the barycentric coordinate with
positive ratio to locate the interior control points of the quartic
form and suggest the symmetrical position of first two points
against the last two points respect to the middle point. From
this assumption, we can automatically avoid the existence of
cusp, loop and the inflexion point. We suggest a simple and
direct method to obtain those approximations which facilitate
to designers. In practice, designers or users usually do not
concern about the underlying mathematics and related
equations. This paper only discusses the curves with second
order of geometric continuity and not extended on higher
order since it is adequate for our objective. Since it involved
the manipulation of quartic form, this will involve a long and
difficult mathematical computation, so the use of CAS
manipulator such as MATEMATICA will make a great help.
The remaining part of this paper is organized as follows. We
start with some preliminary background and notation in Section
II. We prescribe the method that used to construct an arc circles
in the given range of the central angle [0, ) T S  in Section III.
In Section IV, we discuss the radial approximation error and
approximation order which based on Hausdorff distance. The
Open Journal of Applied Sciences
Supplement：2012 world Congress on Engineering and Technology
132 Cop
y
ri
g
ht © 2012 SciRes.

result is compared to the others best known methods. We
present the result of a numerical example in Section V. Finally,
we conclude our results in the final section.
2. Some Preliminary
The following notations and conventions are used. We write
the dot product of two vectors,
A
and
B
as
A
Bx. The
notation of
A
B represents the outer product of two plane
vectors
A
and
B
. Note that the dot and outer products are
scalar which are written as cosAB AB
T x and
sinABAB T  , respectively, where T is the turning
angle from
A
to B. Positive angle is measured anti-
clockwise. The Euclidean norm or length of vector
A
is
A
.
Planar quartic Bezier curve
>@
2
:0,1Zo\ is represented as

44
0
4
() 1
i
ii
i
i
Z
tP tt


§·
¨¸
©¹
¦ , 01tdd, (1)
where i
P
, 0,1, 2, 3,4i are the control points,

4
41
i
ii
tt


§·
¨¸
©¹ is the Bernstein polynomial and t is global
parameter. We denote the end points as 0 P and 4 P, also
j
P,
1,2, 3 j as the interior points. As a planar parametric curve,
the signed curvature of 

Z
t is defined as in [9]:
3
'( )"( )
() '( )
Z
tZt
t
Zt
N

(2)
The signed radius is the reciprocal of (2). It is known that
()t N is positive sign when the curve segment bends to the left
and it is negative sign if it bends to the right at t. '( )
Z
t and
''( )
Z
t are first and second derivatives of (1).
3. Prescribing Methods
In this section, we describe an approach for approximating
the given data. The problem that we considered can be
expressed in following problem statement;
Let 0
P and 4 P be the two points on the circumference of
circle with radius r, and 0
T and 1 T be the unit tangent
vectors, respectively. The central angle of this two point is in
the interval of 0
TS d . Find an approximation of a
circular arc that satisfies this given data by using a single
Bezier quartic curve.
Firstly, we denote
s
P as the intersection point between two
tangent lines parallel to unit vector ,
i
T 0,1i , that pass
through endpoints 0 P and 4 P, respectively. Here, we only
consider the construction of curve segment that is negative
curvature, whereby for approximation of arc circle with
positive curvature is in the similar manner. According to
Grandine and Hogan [6], S P can be achieved by
410001
01
()()
S
PTTT PT
PTT

 (3)
If we denoted 0 B as the centre of the circle, so the circular arc
is divided symmetrically by line 0S PB . By using the
barycentric coordinate, the interior points 123 ,,PPP
may now
be written in the terms of 04
,,
S
P
PP as


10
1S
P
PP
U
U ,


34
1S
P
PP
U
U , (4)

213
12 S
P
PP P DD D .
Point 1 P and 3 P are in barycentric form of 2 points, where
their barycentric coordinates were 

,1
U
U and


1,
U
U ,
respectively. While 2 P is a barycentric combination of 3
points with coordinate


,,12 DD D . All of those coefficients
satisfy 0,1 DU  . Without any loss of generality in terms of
translation, rotation, reflection and uniform scaling, we can
allocate 0
P
, 4
P
on same ordinate, while S
P
on y-axis and
the center of the circle 0
B
on the origin. Fig. 1, shows the
position of these control points and their interior points
123
,,
P
PP
with respect to the canonical positions.
P
4
P
0
P
1
P
2
P
3
P
S
ǂǂ
1 ǂ 2 ǂ
ǂ
1 ǂǂ 1 ǂǂ
ǂ
Fig. 1 Position of control points and their barycentric coordinates
Secondly, since our objective is to obtain the sufficient
condition of a single segment of Bezier quartic to approximate
arc circle with 2 G continuity condition, hence we fix




011/r NN  and forced the curvature at median point
as


0.51/r N . Furthermore, we apply 0(0,0)B and
Cop
y
ri
g
ht © 2012 SciRes.133

1r since this do not give any effect on
U
and
D
in general
on curvature analysis. The following procedure shows in detail
how the curvature is obtained. It starts by letting
001
00 0
401
(-),
-,
-,
S
PB TT
PBrN
PBrN
Q 
(5)
where Q is a constant. 0 N and 1 N are unit normal vectors of
0
T and 1 T at 0 P and 4 P, respectively. Since we considering
the arc circular of negative curvature then 00
0TN and
11
0TN. Substituting (4), (5) into (1) give

Z
t in the
terms of unit vectors as

10 2130 41
Z
taNaNaTaT  (6)
where





2
1
2
1.
1361424
art
tt DUU U

 ,
 
 
2
2
2
36 14,
614131
t
art
t
DUU
DUD U
§·

¨¸
¨¸
 
©¹
(7)
 

 
2
3
36 142
21 ,
3614
t
att
t
DUUU
QDUU
§·

¨¸
¨¸

©¹
43
.aa 
The first derivative of

Z
tis

10 2130 41
'''''
Z
taNaNaTaT 
. (8)
And the second derivative of


Z
t is

10 2130 41
'''''''''' .
Z
taNaNaTaT 
(9)
Here, '
j
a and ''
j
a are first and second derivatives of
j
a,
1, 2,3,4j , respectively. By using the prior conventions,
several product vectors and the related coefficient Q
is
obtained as follow
 
00 0011
11001 1
00 1100
001 111
00100 101
010 00110
41 11
01 01
1
0
sin ,
cos ,
sin
NN TTNN
TTNTN T
NTNTNN
TTN NTT
NTNTTTNN
TT NNNT NT
PT rNTr
TT TT
T
T
QT
 

  
  
 


<<<
<
<<
<<
<<
(10)
By applying (8), (9) and (10) onto (2), the numerator and
denominator of curvature, N can be write as
 

13 24 4231
21 122332
43 341441
''''''''''''' ''
''''''sin''''''cos
''''''sin''''''cos,
ZZ aaaa aaaa
aa aaaaaa
aa aaaaaa
TT
TT
 
 
 
(11)


2222
1234
14 2312 34
''''''
2''''sin 2''''cos
ZZ aaaa
aa aaaa aa TT

 
<. (12)
Since as fixed earlier that


011 NN , we achieve

3
2
31cossin csc
22 1
TT
DU T
U

. (13)
And as 1/2t , so for

1/2 1 N , simplification yield to
  

3
12 12132sincsc
21
32
T
DU UT
U
 

. (14)
From (13), D can be write in the terms of
U
and /2 T ) as

22
2sec
31
U
D
U
)
. (15)
Substituting (15) into (14), we get the quadratic equation in
the terms of
U
as follows



23
48sec12 96sec0 UU )) . (16)
It is clear from (16) that if 2
cos 3 )t then we get two positive
values of
U
. The result is obtained from


96sec0 )d
which come directly from Descartes’s Rule of Signs. And
from the discriminate of (16) we prove that there exist two real
values as shown below

2
961 sec12secsec0)))t . (17)
134 Cop
y
ri
g
ht © 2012 SciRes.

If we name 12 ,
UU
as the solutions of (16), we obtain

2
13
361 sec12secsec,
24sec
U
)))
) (18)

2
23
361 sec12secsec.
24sec
U
)))
) (19)
Finally, by substituting each of these solutions into (15),
we obtain the values of D that satisfies (13) and (14). As the
result,

11
,
U
D and

22
,
U
D are two possible values that give
us the necessary condition to approximate the given problem.
Fig. 2 shows the function of 1
U
and 2
U
given in plain and
dashed curves, respectively, which referred to 0/2 S d) .
Positive value of 1
U
is
>
@
0,0.5 since interval of ) is
1
0,cos (2/3)

ªº
¬¼
.
ǂ
1
ǂ
2
0
.5 1.0 1.
5
ǂ 0.1
0.1
0.2
0.3
0.
4
0.
5
Fig. 2 Value of 1
U
and 2
U
for 0/2 S d)
Since 2
U
has bigger range of ) compare to his counterpart
1
U
, so for further discussion we only consider 2
U
where we
obtain an approximate curve which satisfies the given problem
in high order of accuracy. The explicit approximate quartic
form which is easy to use can been stated as follows.
An approximation quartic Bezier of circular arc can be
found by using (1), with control points as (4) and (3), where
U
as (19),
D
from (15) and the central angle is


1
01 0
1
01 0
sinif 0
sinif 0
TT TT
TT TT
TS


t
°
® 
°
¯
<
<
(20)
It is clear that the parameters D and
U
are depend on the
central angle that has been created by the end points. Here,
T
as specified in (20) satisfy the acute and obtuse angle.
4. Approximation Accuracy Analysis
In this section we discuss the accuracy of the approximation
that make by the quartic Bezier form which introduced in the
previous section. The approximation accuracy is obviously
considered as a distance between set of points on given curves,
i.e., a circular arc and a quartic curve in this case. Here we will
consider Hausdroff distance as proposed by Ahn and Kim [1],
where it is most reliable scheme to measures how far two
subsets of a Euclidean space are from each other. The
Hausdorff distance can be described as the longest distance
between two ste of points. First, let us consider b as the arc
circle, so the Hausdroff distance between the arc circle and the
approximation arc can be derived as follows


>@


0,1
,max,
Ht
dbZ t H

(21)
where
 
22
1txtyt H 
. (22)
The function in (22) is known as the radical error, and another
alternative error function that has been used for the analysis is






22
1txtyt \ 
. (23)
Function (22) and (23) have their zero sets and extreme
values at the same locations, however using (23) is preferable
since there is no square root term involved. It can be shown
that when


t \
is small, then




2tt
\
H | as in [4]. We use
those two error functions in order to determine the
approximate errors and for comparisons manner.
We locate the end points of arc circle at


11, 0P ,


4cos,sinP ))
with center of the unit circle is


00,0B . Since we consider the minor arc circle with
positive curvature therefore the unit tangent vectors at 04 ,PP
are


00, 1T and


1sin ,cosT )), respectively. As a
result of substituting 01
(-)/sin2
S
PrTT )
and (4) into (1),
the components of quartic curve ()
Z
t is simplified as


434
22
3
()(-1 )-4(-1 )cos2
-6(-1)-1(-1)cos2
4(1-)cos2-cos2,
xttt tt
tt
tt
DDUDU
UU
)
)
))
(24)
and


33
2
2
()
sin 2- 4(-1)tan
-6(-1)-1(-1)cos 2tan
4(-1)sin2 - cos2 tan
yt
tt
ttt
tt
U
DDUD U
U
§·
))
¨¸
 ))
¨¸
¨¸
¨¸
) ))
©¹
. (25)
So


t \ and it’s derivative


't \ , respectively are

2
3
223 1
11 2
x
yBttt k
§·
§·
 
¨¸
¨¸
¨¸
©¹
©¹
, (26)
Cop
y
ri
g
ht © 2012 SciRes.135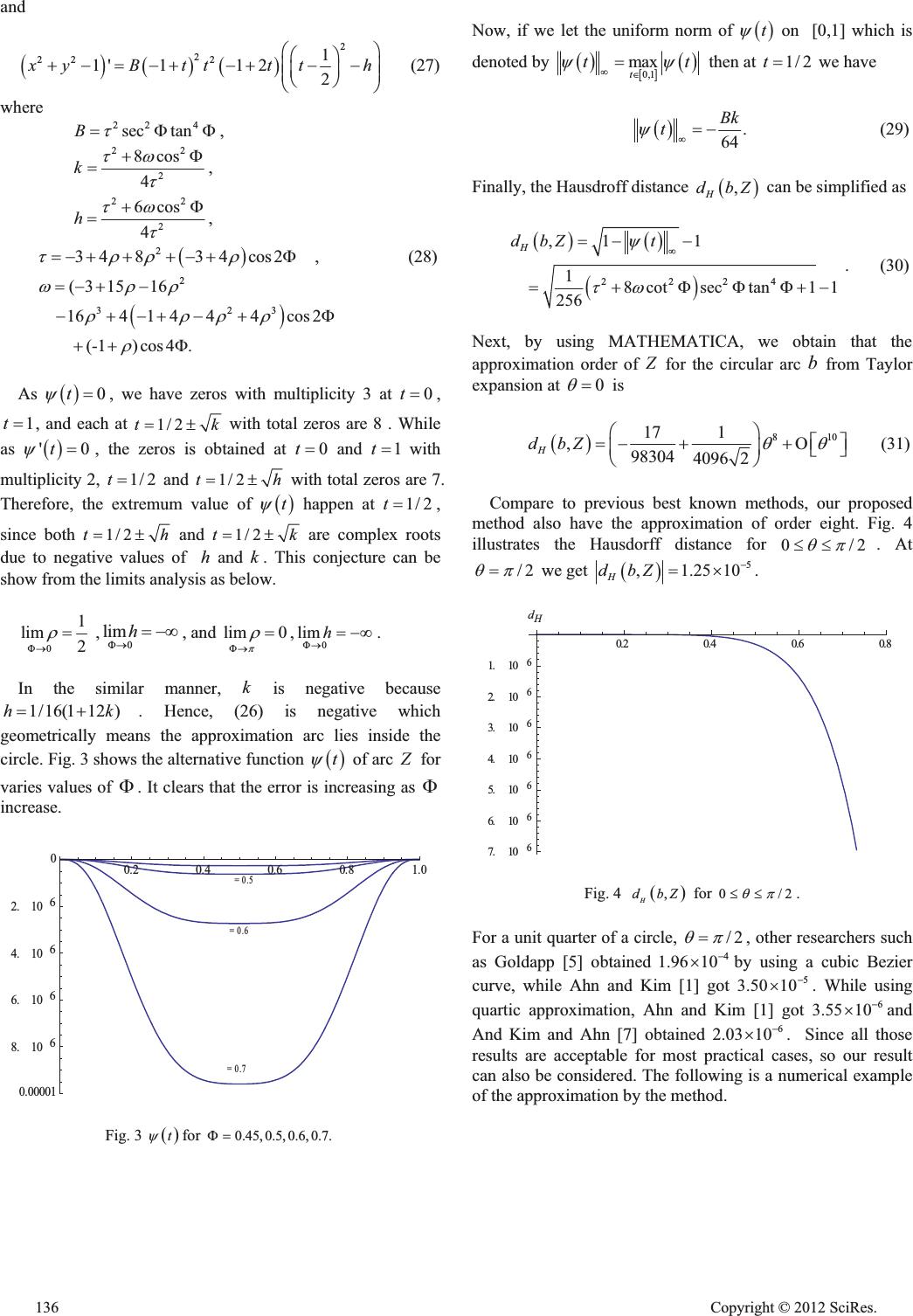

and

 
2
2
222 1
1'11 22
x
yBtttth
§·
§·
 
¨¸
¨¸
¨¸
©¹
©¹
(27)
where
22 4
sec tanB W )),
22
2
8cos
4
k
WZ
W
)
,
22
2
6cos
4
h
WZ
W
)
,

2
34834 cos2 WUU U ) , (28)

2
323
(3 1516
1641444cos2
(-1)cos4.
ZUU
UUUU
U

 )
 )
As


0t \ , we have zeros with multiplicity 3 at 0t ,
1t , and each at 1/2tk r
with total zeros are 8 . While
as

'0t \ , the zeros is obtained at 0t and 1t with
multiplicity 2, 1/2 t and 1/2th r
with total zeros are 7.
Therefore, the extremum value of


t \
happen at 1/2
t ,
since both 1/2th r and 1/2tk r are complex roots
due to negative values of h and k. This conjecture can be
show from the limits analysis as below.
0
1
lim 2 U
)o
,0
limh
)o f, and lim0
S
U
)o
,0 lim h
)o f.
In the similar manner, k is negative because
1/16(112 )hk . Hence, (26) is negative which
geometrically means the approximation arc lies inside the
circle. Fig. 3 shows the alternative function


t \ of arc
Z
for
varies values of ). It clears that the error is increasing as )
increase.
= 0.7
= 0.6
ǂ = 0.5
0.2 0.4 0.6 0.8 1.0
ǂ 0.00001
ǂ 8. ǂ 10
ǂ 6
ǂ 6. ǂ 10
ǂ 6
ǂ 4. ǂ 10
ǂ 6
ǂ 2. ǂ 10
ǂ 6
0
Fig. 3 
t \
for 0.45, 0.5, 0.6, 0.7.)
Now, if we let the uniform norm of


t \ on [0,1] which is
denoted by


>@


0,1
max
t
tt \\
f
then at 1/2t we have

.
64
Bk
t
\
f  (29)
Finally, the Hausdroff distance


,
H
dbZ can be simplified as
 

2224
,1 1
1
8cotsectan11
256
H
dbZ t \
WZ
f

)))
. (30)
Next, by using MATHEMATICA, we obtain that the
approximation order of
Z
for the circular arc b from Taylor
expansion at 0
T is

810
17 1
,98304 4096 2
H
dbZ TT
§·
ªº
2
¨¸
¬¼
©¹
(31)
Compare to previous best known methods, our proposed
method also have the approximation of order eight. Fig. 4
illustrates the Hausdorff distance for 0/2 TS dd . At
/2 TS we get


5
,1.2510
H
dbZ  u.
0
.
2
0
.
4
0.6 0.8
ǂ 7. ǂ 10
6
ǂ 6. ǂ 10
6
ǂ 5. ǂ 10
6
ǂ 4. ǂ 10
6
ǂ 3. ǂ 10
6
ǂ 2. ǂ 10
6
ǂ 1. ǂ 10
6
d
H
Fig. 4


,
H
dbZ for 0/2 TS dd .
For a unit quarter of a circle, /2 TS , other researchers such
as Goldapp [5] obtained 4
1.96 10 uby using a cubic Bezier
curve, while Ahn and Kim [1] got 5 3.50 10 u. While using
quartic approximation, Ahn and Kim [1] got 6
3.55 10 uand
And Kim and Ahn [7] obtained 6
2.03 10 u. Since all those
results are acceptable for most practical cases, so our result
can also be considered. The following is a numerical example
of the approximation by the method.
136 Cop
y
ri
g
ht © 2012 SciRes.

I. NUMERICAL EXAMPLE
Given the following data,
0
13
,
22
P§· 
¨¸
¨¸
©¹
, 4
13
,
22
P§· ¨¸
¨¸
©¹
,
0
31
,
22
T§· ¨¸
¨¸
©¹
, 1
31
,
22
T§· 
¨¸
¨¸
©¹
, 1r .
Substituting the given data into (20), (19), (15), (3) and
followed by (4), we have the following results
0.3451 D , 0.4585
U
,

0,1.1547
S
P ,

10.2707,0.9984P ,

20,1.0468P ,

30.2707,0.9984P
So from (1), we obtained the quartic Bezier that satisfies the
given data. We illustrate this approximation curve as shown in
Fig. 5, where the approximate curve is in plain arc and the
standard arc circle is in dashed arc. Note that the
approximation arc is coinciding with the standard arc circle.
P
4
P
0
P
1
P
2
P
3
P
S
Fig. 5 An approximate curve and a standard circular arc
5. Conclusion
We present a method that give quick finding of an
approximate curve to circular arcs by a single segment of
quartic Bezier curve. An approximate curve can be
straightforward blended on given two points with prescribed
locations and directions on the circumference of a circle. The
setting of interior control points of quartic Bezier curve is
defined from a set of barycentric coordinate which
geometrically understandable by users and give the curvature
continuous approximation of degree two. Compared to the
other previous methods, the approximation order of this
proposed method is also eight. Although the order of accuracy
of the proposed method is less than the best previous known
results, our introduced quartic Bezier form has the advantage
of easily counter the constrained 2 G Hermite interpolation
problem by combination through S,C-shape of a single cubic
or quartic transition curve. Also we can easily extend the
result to find the spline arc, which will reduce the error of the
approximation or to construct an arc of central angle
2 ST S dd .
6. Acknowledgment
The authors are very grateful to the anonymous referees for
their valuable suggestions. This work was supported by the
Ministry of Higher Education of Malaysia FRGS (2010-0066-
102-02).
REFERENCES
[1] Ahn Y.J. and Kim H.O. Approximation of circular arcs by
Bezier curves. Computer Aided Geometric Design,
81:145-163, 1997.
[2] deBoor C., Hollig K. and Sabin M. High accuracy
geometric Hermite interpolation. Computer Aided
Geometric Design, 4:269–278, 1987.
[3] Dokken T. , Dehlen M., Lyche T and Morken K. Good
approximation of circles by curvature-continuous Bezier
curves. Computer Aided Geometric Design, 7:33-41,
1990.
[4] Fang L. Circular arc approximation by quintic polynomial
curves. Computer Aided Geometric Design, 15:843-861,
1998.
[5] Goldapp M., Approximation of circular arcs by cubic
polynomial. Computer Aided Geometric Design, 3:227-
238, 1991
[6] Grandine T.A and Hogan T.A. A parametric quartic
spline interpolant to position, tangent and curvature.
Computing (DOI), 72:65-78, 2004.
[7] Kim S.H. and Ahn Y.J. An approximation of circular arcs
by quartic Bezier curves. Computer Aided Geometric
Design, 30:490-493, 2007.
[8] Riskus A. Approximation of a cubic Bezier curve by
circular arcs and vice versa. Information Technology and
control, Vol 35, 4:371-378, 2006.
[9] Yamaguchi F. Curves and surfaces in computer aided
geometric design. Springer-Verlag 1988
[10] Žagar, Emil, Jakliþ, Gašper, Kozak, Jernej, Krajnc,
Marjeta. Approximation of circular arcs by parametric
polynomial curves . Annali Dell'Universita' di Ferrara,
53;2:271-279, 2007.
Cop
y
ri
g
ht © 2012 SciRes.137