Dynamic Contact Problem for Slide Hinge
Kazunori Shinohara
JAXA's Engineering Digital Innovation Center (JEDI)
Japan Aerospace Exploration Agency (JAXA)
Sagamihara, Japan
Ryoji Takaki
Institute of Space and Astronautical Science (ISAS)
Japan Aerospace Exploration Agency (JAXA)
Sagamihara, Japan
Takeshi Akita
Faculty of Engineering
Chiba Institute of Technology
Chiba, Japan
Abstract—Contact analysis can be either static or dynamic. In static contact analysis, the position on the contact surface is
constant. In dynamic contact analysis, the position on the contact surface changes at every time step. In static contact analysis, the
computing results (stress, strain, etc.) of contact states have been verified through the Hertz contact problem in literature. On the
other hand, there has been insufficient research into dynamic contact analysis. The contact algorithm is insufficiently constructed
in finite element model (FEM) discretization. The gap between two objects cannot be calculated accurately. A contact method is
demanded for artificial parameters. Inappropriate setting of artificial parameters causes artificial numerical oscillations on the
contact surface between objects. To develop a high-reliability satellite, we started the development of FEM contact-friction
modeling techniques in this study. A dynamic contact method was realized by using the appropriate parameters required in the
contact analysis. We verified the reproducibility of the physical behavior of the contact friction via numerical simulation
techniques by using a computational model of the hinge joints.
Keywords-FEM; Contact; Friction; Stress; Joints; Structural Analysis; Advance/FrontSTR; Dynamic Contact Analysis; Static
Contact Analysis
1. Introduction
This year, failures due to joints between parts have become
apparent [1]-[3], as high-precision equipment of space
structures are demanded. Various contaminants in the air on the
ground adhere to the contacting parts of metal surfaces. These
contaminants, in turn, act as a lubricant, thereby reducing the
coefficient of friction. Therefore, the frictional force on the
contact surface is naturally decreased on the ground. Space,
however, is a vacuum, and because metal contamination does
not occur in space, the friction coefficient between the metals
in space increases to about 10 times that on the ground [4]. In
space, the friction force causes incomplete movement at joints
because of the lack of lubrication.
In this study, to develop the high-precision space structure,
we construct a simulation based on contact-friction finite
element analysis (FEM) using Advance/FrontSTR [5]-[7]. The
accuracy of the calculated results using Advance/FrontSTR is
verified. To develop high-reliability satellites, we started the
development of contact modeling techniques by using a
high-performance computer (JSS) in this study. The contact
behaviors were verified by using computational joint models of
the slide hinge.
2. Contact-friction analysis [6] [8]
The variable ȡ represents the density. The subscript curly
brackets of variables represent object {1} and object {2}. The
superscript ˆ represents the known variables. The sign · and
the sign : represent the inner product of the first order
tensor and second order tensor, respectively. The sign ȍ{i}
represents the internal domain of objects. Signs Ȗ{1} and Ȗ{2}
represent the traction boundary conditions. The non-index Ȗ
represents the contact surface between objects. The sign ѭ
ѭ
represents nabla. The boundaries ī{1} and ī{2} represent the
displacement boundary conditions. The tensor ı represents the
Cauchy stress tensor. The vector g represents the gravity vector.
The vectors v and
v

represent the velocity vector and
acceleration vector, respectively. The vectors n, u, and s
represent the outward normal vector, the displacement vector,
and the surface traction vector, respectively. The function u*
represents arbitrary weighting functions. Governing equations
including moving objects consist of the force balance, the
displacement boundary conditions, and the traction boundary
conditions.
^`^`^` ^`^` iiiii
in : vgı U
(1)
^` ^`^`^` iiii
on J snıˆ 
(2)
Open Journal of Applied Sciences
Supplement：2012 world Congress on Engineering and Technology
82 Cop
y
ri
g
ht © 2012 SciRes.

^` ^`^`^` iiii
on J snı 
(3)
^` ^`^` iii on * uu ˆ
(4)
Governing equations including moving objects consist of
the force balance, the displacement boundary conditions, and
the traction boundary conditions. Using the force balance (1)
and the arbitrary weighted function, the residual equation is
derived as follows:
^`^`^` ^`

^` ^`
^`
^`
2,10
* : :
³
:iindiiiiiii
i
uvgı U
(5)
Using the partial integration based on Gauss-Green’s
theorem, (5) is transformed as follows:
^`^`^`^` ^`^` ^`

^`
^`
^`^` ^`
^`
^` ^`^`
2,10
ˆ
:
**
***
: 
:
³³
³:
iindd
d
iiiiii
iiiiiiii
i
i
JJ JJ
U
usus
uguvuı
(6)
Equation (6) is transformed as follows:
^` ^`

^`
^`
^`^` ^`^` ^`

^`
^`
^`^` ^`
^`
^`^`^ `
^`
^` i
ii
iii
i
iiiiii
i
iii
indd
dd
i
ii
: 
::
¦³ ¦³
¦³ ¦³
: :
0
ˆ
:
2
1
*
2
*
11
2
1
*
2
1
**
2
1
*
JJ
JJ
U
uusus
uguvuı
(7)
3. Algorithm of Contact-Friction
Analysis
In this study, the Advance/FrontSTR and JAXA
supercomputer system (JSS) are applied to solve the
contact-friction problem. Advance/FrontSTR was
jointly-developed as part of a government project (Ministry of
Education, Culture, Sports, Science and Technology) by the
University of Tokyo (Prof. Hiroshi Okuda) and Advance Soft
Co. Ltd. Presently, Advance Soft Co. Ltd. provides commercial
versions of the software and is responsible for upgrades. The
software can calculate the geometric non-linearity, the material
non-linearity, and the contact non-linearity. The JSS consists of
a massively parallel supercomputing system, a storage system,
a large-scale shared memory system, and a remote access
system. We attempted to realize a large-scale FEM analysis of
the high efficient parallel supercomputing system by
Advance/FrontSTR and JSS. The increments of displacements
are unknown variables at the nodes in the FEM model. The
displacement can be obtained by the increments of
displacements. The strain can be subsequently calculated by
the displacement. Then, the stress can be calculated by the
stress-strain relationship. Advance/REVOCAP is applied for the
pre-processing and the post-processing. Advance/REVOCAP
can easily make FEM meshes, set calculation conditions, and
visualize results from Advance/FrontSTR [5][6].
4. Calculation results
A.Slide hinge model
Fig.2 shows the computing model. The structure consisted
of a hollow cylinder and a ring. The hollow cylinder makes
physical contact with the ring. The outer and inner diameters of
the ring were 10.0 and 12.0 (mm), respectively. The length in
the longitudinal direction (direction z) was 20.0 (mm). The
outer and inner diameters of the hollow cylinder were 10.0 and
8.0 (mm), respectively. The length in the longitudinal direction
(direction z) was 150.0 (mm). There were 4640 nodes and 2240
elements. The element type was applied to the first-order
hexahedral element. For the material properties, the Young's
modulus, Poisson ratio, and density were set to 2.03 × 105
(N/mm2), 0.3, and 7.85 × 10-6 (kg/mm3), respectively. The
displacements on both sides were fixed as boundary conditions.
Using this computing model, we conducted the static and
dynamic contact analyses. In static contact analysis, the
position on the contact surface does not change with respect to
time. On the other hand, in dynamic contact analysis, the
position on the contact surface does change with respect to
time.
Figure 1 Computer model (by Advance/REVOCAP [5]).
Figure 2 Computing model of sliding hinge (by Advance/REVOCAP [5])
B.Static Contact Analysis of Slide Hinge Model
Fig.3 shows the strain contour and deformation (scale
factor: 1 × 105). The center of the cylinder bent under the
influence of the ring weight. Fig.4 shows the strain contour.
Fig.5 shows the strain distribution for the red line on the
cylinder and blue line on the ring in Fig.4. The vertical axis
represents the radial strain. The horizontal axis represents the
coordinates with respect to the z direction in Fig.4. Red line (1)
represents the line (x = 0, y = 10) on the cylinder. Red line (2)
represents the line (x = 0, y = -10) on the cylinder. Blue line (3)
represents the line (x = 0, y = 10) on the ring. Blue line (4)
represents the line (x = 0, y = -10) on the ring. As shown in
Fig.5, in order to deform the cylinder under the ring weight, the
strain distribution of the cylinder was larger than that of the
ring. Fig.6 shows the radial stress distribution along the cross
section z = 0. The radial strain was plotted at every angle going
in the counterclockwise direction. The yellow circle in Fig.6
represents 0.0. For plots inside the yellow circle, the direction
of the radial strain vector was inward toward the center of the
Cop
y
ri
g
ht © 2012 SciRes.83

circle. For plots outside the yellow circle, the direction of the
radial strain vector was outward toward the center of the circle.
In static contact analysis, the strain distribution on the ring
surface did not agree with that on the cylinder surface. The
radial strain on the cylinder surface was greater than that on the
ring surface.
Figure 3 Strain distribution and deformation (Scale factor: 1 × 105)
Figure 4 Strain contour
Figure 5 Radial strain distribution with respect to z axis
Figure 6 Radial strain distribution with respect to circumferential direction
C.Dynamic contact analysis of slide hinge model
The cylinder was inclined at a 45° angle with respect to the
gravity vector. Strain distributions were calculated when the
ring slipped to 33 (mm) in the z direction. The slip velocity of
the ring was 8.3 (mm/s). The coefficient of friction was set to
0.0. The radial strain distribution is shown in Fig.12. The
horizontal axis represents the distance along the z axis. As
shown in Fig.9, the original point o’ represents the slip point 33
(mm) from the original point o in the initial position (Fig.4).
The vertical axis represents the radial strain. The radial strain
increased monotonically from the negative side of the z
coordinate to the positive side of the z coordinate. The strain
calculated by dynamic contact analysis was greater than that
calculated by static contact analysis, shown in Fig.6. As shown
in Fig.13, the strain distribution with respect to the
circumferential direction was visualized along the cross section
z = 0. The radial strain on the contact surface of both the
cylinder and the ring was positive at every angle. Radial strains
on the upside and the downside were greater than those on the
right and left sides. In static contact analysis, the radial strain
distribution of the ring was different from that of the cylinder.
On the other hand, in dynamic contact analysis, the radial strain
distributions of the ring and cylinder almost agreed with each
other. Figs.10 and 11 show the time history of the slip velocity
of the ring. The slip velocity in the z direction increased. The
slip velocity in the y direction caused a vibration, as shown in
Fig.11. Vibration dampened with time.
Figure 7 Strain contour figure (1.9 (s))
Figure 8 Strain contour figure (4.6 (s))
84 Cop
y
ri
g
ht © 2012 SciRes.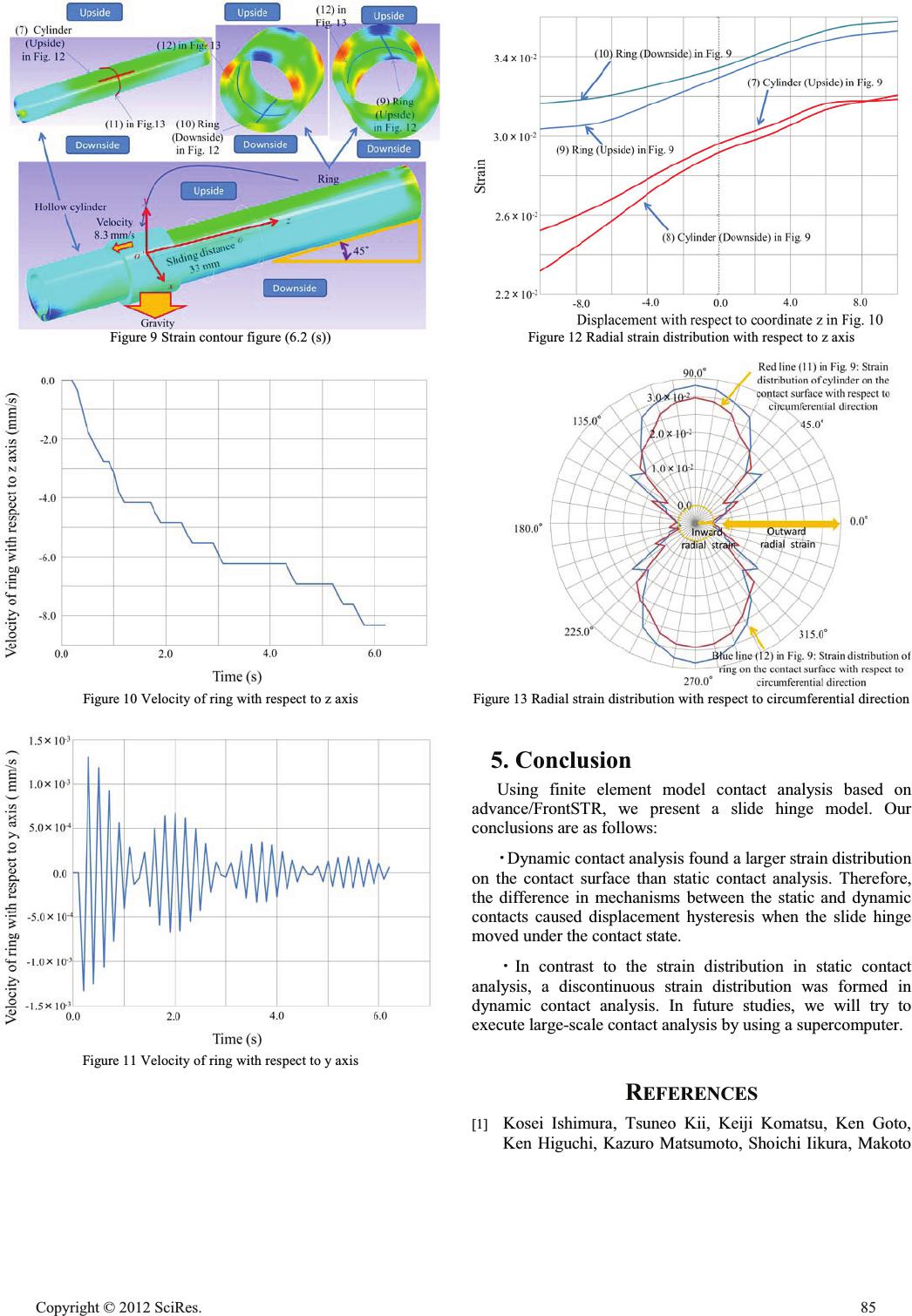

Figure 9 Strain contour figure (6.2 (s))
Figure 10 Velocity of ring with respect to z axis
Figure 11 Velocity of ring with respect to y axis
Figure 12 Radial strain distribution with respect to z axis
Figure 13 Radial strain distribution with respect to circumferential direction
5. Conclusion
Using finite element model contact analysis based on
advance/FrontSTR, we present a slide hinge model. Our
conclusions are as follows:
࣭Dynamic contact analysis found a larger strain distribution
on the contact surface than static contact analysis. Therefore,
the difference in mechanisms between the static and dynamic
contacts caused displacement hysteresis when the slide hinge
moved under the contact state.
࣭In contrast to the strain distribution in static contact
analysis, a discontinuous strain distribution was formed in
dynamic contact analysis. In future studies, we will try to
execute large-scale contact analysis by using a supercomputer.
REFERENCES
[1] Kosei Ishimura, Tsuneo Kii, Keiji Komatsu, Ken Goto,
Ken Higuchi, Kazuro Matsumoto, Shoichi Iikura, Makoto
Cop
y
ri
g
ht © 2012 SciRes.85

Yoshihara, and Masaharu Tsuchiya, Shape Prediction of
Large Deployable Antenna Structure on Orbit,
Transactions of the Japan Society for Aeronautical and
Space Sciences, Aerospace Technology Japan, 10(2012).
[2] Hiroshi Kitahara, Kiku-6's Unsuccessful Injection into
GEO: Then and Afterwards, The Journal of the Institute of
Electronics, Information, and Communication Engineers
80(1997), pp. 570-575.
[3] Hiraku Sakamoto, Nicholas Ragosta, and Mori Osamu,
Finite-element Analysis of Membrane Deployment and Its
Validation, Proceedings of 55th Space Sciences and
Technology Conference, paper No.1B08, (2011).
[4] Donald H. Buckley, Friction, Wear and Lubrication in
Vacuum, NASA-SP-277, 1971.
[5] AdvanceSoft. Co., Ltd., http://www.advancesoft.jp/.
[6] Xi Yuan, Theory reference on nonlinear analysis of
Advance/FrontSTR Ver.3.0, Advance Simulation, vol. 4,
pp. 6–59, 2010.
[7] FrontISTR, http://www.ciss.iis.u-tokyo.ac.jp/.
[8] Klaus Jurgen Bathe, Finite Element Procedures, New
Jersey, Prentice Hall, 1995.
86 Cop
y
ri
g
ht © 2012 SciRes.