Paper Menu >>
Journal Menu >>
 Unification and Application of 3-point Approximating Subdivision Schemes of Varying Arity Abdul Ghaffar*, Ghulam Mustafa† Department of Mathematics The Islamia University of Bahawalpur Bahawalpur, PAKISTAN *gulzarkhan143@yahoo.com, Beijing 100084, P. R. CHINA †ghulam.mustafa@iub.edu. pk Kaihuai Qin Dept. of Computer Science & Technology Tsinghua University Corresponding author: E-mail: qkh-dcs@tsinghua.edu.cn Abstract—In this paper, we propose and analyze a subdivision scheme which unifies 3-point approximating subdivision schemes of any arity in its compact form and has less support, computational cost and error bounds. The usefulness of the scheme is illustrated by considering different examples along with its comparison with the established subdivision schemes. Moreover, B-splines of degree 4and well known 3-point schemes [1, 2, 3, 4, 6, 11, 12, 14, 15] are special cases of our proposed scheme. Keywords-component; Approximating subdivision scheme; binary; ternary; ࢇ-ary; continuity and Laurent polynomial MSC (2000): 65D17, 65D07, 65D05. 1. Introduction In recent years, subdivision schemes has becomeone of the most popular methods of creating geometric objects in computer aided geometric design and animation industry. Their popularity is due to the facts that subdivision algorithms are easy to implement and suitable for computer applications. Subdivision schemes can be classified into approximating and interpolating ones. The beginning of the subdivision story can be dated back to the papers of Chaikin [2] over thirty years ago, but the idea of families of subdivision schemes of higher arity is relatively new. Based on wavelet theory, Lian [8] introduced 2݉െpoint ܽ-ary for any ܽ2 and (2݉ + 1) െpoint ܽ-ary for any odd ܽ3 interpolatory subdivision schemes for curve design. These schemes include the extended family of the classical 4- and 6-point interpolatory Į-ary schemes [9] and the family of the 3- and 5-point ܽ- aryinterpolatory schemes [10]. Mustafa and Khan [7] offered a new 4-point quaternary approximating subdivision scheme. Siddiqi and Rehan [15] introduced a modified form of binary and ternary 3-point subdivision schemes which are C1and ܥ2 in the intervals ቀെ1 8,1 5ቁand ቀെ1 72,7 72ቁrespectively. Most work in the area of subdivision schemes has considered binary and ternary schemes. But the research communities are gaining interest in introducing higher arity schemes (i.e. ternary, quaternary,…,݊-ary) that give better results and less computational cost. This motivates us to present the family of schemes with higher arity and more degree of freedom for curve designing. We decided to investigate schemes with an odd number of control points, specifically 3-point schemes. This led to a more general investigation of higher arity subdivision schemes. In this paper 3-point subdivision schemes are extended to Į-ary 3-point approximating subdivision schemes for any integer ܽ2.In ܽ-ary 3-point approximating subdivision schemes, we introduced new families of subdivision schemes for curve design. The first family is binary approximation, second is ternary approximation and onto ܽ- ary approximation. A general formula for the mask of ܽ-ary 3-point approximating subdivision scheme is defined as follows Ƚ3 ܽ(ݖ)=1 (2ܽ)2൬1െݖܽ 1െݖ൰3൭൬2݅൰ݖ݅ 2 ݅=0൱, (1) where “ܽ” represents the arity. In this paper we recall basic definitions and preliminary results in Section II. The family of ܽ-ary 3-point approximating scheme is presented in Section III. Comparison with the existing 3-point scheme, basic properties of the limit function, error analysis and effect of parameters ܽ-ary 3-point schemes are discussed in Section IV. Conclusion isalso discussed in Section IV. I. ANALYSIS OF THE GENERAL ܽെARY SCHEME A general form of univariatea-ary subdivision scheme S which maps a polygon ^` = i i kk ff to a refined polygon ^` Zi k i k ff 1 1 is defined by ݂݅݇+1=ߙ݆ܽെ݂݆݅݇, ݅אܼ (2 ݅אܼ ) where the set ߙ={ߙ݅:݅אܼ}of coefficients is called the mask at ݇-th level of refinement. Anecessary condition for the uniform convergence of subdivision scheme (2) is Open Journal of Applied Sciences Supplement:2012 world Congress on Engineering and Technology 48 Cop y ri g ht © 2012 SciRes.  ߙ݆ܽ= ݅אܼ ߙ݆ܽ+1= ݅אܼ ߙ݆ܽ+2= ݅אܼ …ߙ݆ܽ+ܽെ1= ݅אܼ 1. (3) A subdivision scheme is uniformly convergent if for any initial data ݂0 = {݂݅0: ݅אܼ}, thereexistsa continuous function ݂ such that for any closed interval ܫ ؿ ܴ, it satisfies ݈݅݉ ݇՜λݏݑ ݅אܽ݇ܫ|݂݇െ݂(ܽെ݇݅)|=0. Obviously, ݂ = ܵλ݂0. Introducing a symbol called Laurent polynomial ߙ(ݖ)=ߙ݅ݖ݅ ݅אܼ , (4) of the mask ߙ={ߙ݅:݅אܼ} which play an efficient role to analyze the convergence andsmoothness of subdivision scheme. From (3) and (4) the Laurent polynomial of convergentsubdivision scheme satisfies ߙ൫݁4݄݅ ߨ/ܽ൯=0, ݄אܼת (0,ܽ)andߙ(1)=ܽ. (5) This condition guarantees the existence of a related subdivision scheme for the divided differencesof the original control points and the existence of an associated Laurent polynomial Į(ݖ) ߙ(1)(ݖ)=ܽݖܽെ1൬1െݖ 1െݖܽ൰ߙ(ݖ). The subdivision scheme ܵ1 with Laurent polynomial ߙ(1)(ݖ), is related to the scheme ܵ withLaurent polynomial ߙ(ݖ) by the following theorem. Theorem 1[5] Letܵdenote a subdivision scheme with Laurent polynomial ߙ(ݖ)satisfying (5). Then there exists a subdivision scheme ܵ1with the property ο݂݇=ܵ1ο݂݇െ1, where݂݇=݂ܵ݇0and ο݂݇={(݂݇)݅=ܽ݇൫݂݅+1 ݇െ݂݅݇൯; ݅א ܼ}. Furthermore, ܵis a uniformlyconvergent if and only if 1 ܵ1converges uniformly to zero function for all initial data݂0, in the sense thatlim ݇՜λ൬1 ܽܵ1൰݂݇0=0. The above theorem indicates that for any given scheme ܵ, with the mask Į satisfying (3), wecan prove the uniform convergence of ܵ by deriving the mask of 1 ܽܵ1and computing ฯቀ1 ܽܵ1ቁ݅ฯλfor ݅ = 1,2,3...,ܮ, where ܮ is the first integer for whichฯቀ 1 ܽܵ1ቁܮฯλ<1.If such an ܮ exists,then ܵ converges uniformly. Since there are ܽ rules for computing the values at the nextrefinement level, so we define the norm ԡܵԡλ =݉ܽݔ൝หߙ݆ܽห, ݅אܼ หߙ݆ܽ+1ห ݅אܼ ,หߙ݆ܽ+2ห ݅אܼ ,…,หߙ݆ܽ+ܽെ1ห ݅אܼ ൡ, (6) and ብ൬1 ܽܵ1൰ܮብλ=݉ܽݔ൝ቚܾ݅+ܽܮ ݊,ܮ ݆ቚ;݅ ݅אܼ =0,1,2,…,ܽܮെ1ቋ,(7) where ܾ[݊, ܮ]=1 ܽܮෑߙ(݊)ቀݖ݆ܽቁ ܮെ1 ݆=0 , (8) and ߙ(݊)(ݖ)=ܽݖܽെ1൬1െݖ 1െݖܽ൰ߙ(݊െ1)(ݖ) =ܽݖܽെ1൬1െݖ 1െݖܽ൰ߙ(ݖ),݊1. Definition 1. The number of points inserted at the level ݇ + 1 between two consecutive points from a level ݇ is called arity of the scheme. In the case when number of points inserted are 2,3,...ܽ, the subdivision schemes are called binary, ternary,..., ܽ -ary, respectively. Figure 1: (a), (b) and (c) represent binary, ternary and quaternary refinement of coarse polygons using (1) for ݊ = 2,3,4, respectively. 2. Family of the general ܉-ary 3-point approximating scheme In this section, we are introducing a family of 3-point ܽ - ary approximating subdivision schemes for curve design for any integer ܽ ı 2, which is an extension of “B-spline”. We have proved this family by using Chaikin [2], Hassan and Dodgson [4]. The Chaikin’s algorithm for curve design introduced in 1974 is given by ൝݂2݅ ݇+1=3 4݂݅݇+1 4݂݅+1 ݇, ݂2݅ ݇+1=1 4݂݅݇+3 4݂݅+1. ݇ (9) About twenty seven years later, it was extended to the 3- point scheme by Hassan and Dodgson and is given by ቐ݂2݅ ݇+1=5 16݂݅െ1 ݇+10 16݂݅݇+1 16݂݅+1 ݇, ݂2݅ ݇+1=1 16݂݅െ1 ݇+10 16݂݅݇+5 16݂݅+1. ݇ (10) The Laurent polynomials of (9) and (10) are ൞ߙ22(ݖ)=1 4ቀ1െݖ 2 1െݖቁ2൫σ൫1݅൯ݖ ݅ 1 ݅=0 ൯, ߙ32(ݖ)=1 16ቀ1െݖ2 1െݖቁ3൫σ൫2݅൯ݖ ݅ 2 ݅=0 ൯. (11) If “ ܽ ” represents the arity, then by generalizing, we get Cop y ri g ht © 2012 SciRes.49  Ƚ3 ܽ(ݖ)=1 (2ܽ)2൬1െݖܽ 1െݖ൰3൭൬2݅൰ݖ݅ 2 ݅=0 ൱. (12) where integers ܽ2. From the coefficients of Laurent polynomial (12), we get the mask Ƚ3 ܽof family of 3-point ܽ- ary approximating subdivision schemes for curve design for any integerܽ 2. By adjusting the shape parameter in eq (12), we get the 3- point ܽ-ary parametric approximatingsubdivision scheme Ƚ3 ܽ(ݖ)=1 (2ܽ)2൬1െݖܽ 1െݖ൰3൭൬2݅൰ߤ݅ݖ݅ 2 ݅=0 ൱, (13) and ܽ 22൬2݅൰ߤ݅=ܽ,ߤ݆=ߤ2െ݆, ݆=0,1. (14) 2 ݅=0 From the coefficients of Laurent polynomial (13) and using (14), we get the mask Ƚ3 ܽ of afamily of the 3-point ܽ- ary parametric approximating subdivision schemes for curve design forany integer ܽ 2. Remark:For a = 2, 3, 4, in (12), we get the mask of the following 3-point binary, ternary and quaternary schemes, re spec t iv ely, ە ۔ ۓ Ƚ3 ܽ=1 16{1,5,10,10,5,1}, Ƚ3 ܽ=1 36{1,5,13,22,26,22,13,5,1}, Ƚ3 ܽ=1 64{1,5,25,38,46,46,38,25,5,1}. For a = 2, 3, 4, in (12) and using (13) we get the mask of the following 3-point binary, ternary and quaternary schemes, respectively, ە ۖ ۔ ۖ ۓ ߙ3ܽ=1 16{ߤ0,4+ ߤ0,12െ2ߤ0,12െ2ߤ0,4+ߤ0,ߤ0}, ߙ3ܽ=1 36൜ߤ0,4 +ߤ0,12+ߤ0,24െ2ߤ0,28െ2ߤ0, 24െ2ߤ0,12+ߤ0,4+ߤ0,ߤ0ൠ , (15) ߙ3ܽ=1 64൜ߤ0,4+ߤ0,12+ߤ0,24+ߤ0,40െ2ߤ0,48 െ2ߤ0, 40െ2ߤ040െ2ߤ0,24+ߤ0,12+ߤ0,4+ߤ0,ߤ0ൠ. 3. Comparison with existing approximating schemes In this section, we will show that the popular existing Chaikin scheme and 3-point schemes arespecial cases of our proposed family of schemes. Here we will also present support of the basiclimit function and compare the error bounds between the limit curve and the control polygonafter the ݇-fold subdivision of the 3-point schemes. A.Special cases Here we see that the existing symmetric schemes are the special cases of our scheme (15). xBy takingߤ0 = 0,ߤ0= െ48߱,ߤ0 = 1,ߤ0 = െ3 2,ߤ0 =2 3+ 4߱,ߤ0 = 1/2and ߤ0 = െ3 2+ 16ߤ in ߙ32, we get the 3-point binary scheme of [2,3,4,6,11,14,15], respectively xBy settingߤ0= ݑ–1 3, ߤ0 =4 3,ߤ0 = െ4,ߤ0 = 1/3 + 4߱ and ߤ0 = 1/2 + 36ߤ in ߙ33, we get the 3-point ternary scheme of Aslam et al. [1, 4, 10, 15], respectively. B.Support of basic limit function The basic function of a subdivision scheme is the limit function of the proposed scheme forthe following data ݂݅0=ቄ1, ݅=0, 0, ്݅0. (16) Theorem 2.The basic limit functions of ܽ߶3 proposed ܽ-ary 3-point approximating schemes have support width ݏ = 3ܽെ1 ܽെ1, forܽ = 2,3,4,...,݉, which implies that it vanishes outside theinterva lቂെ3ܽെ1 2(ܽെ1),3ܽെ1 2(ܽെ1)ቃ. Figure 2: In this figure (a), (b), and (c) represent the basic limit functions of 3-point binary, ternary andquaternary schemes, respectively. C.Error bounds In Table 1 by using [13], with ߯ = 0.1, we have computed the error bounds between limit thecurve and the control polygon after the ݇-fold subdivision of the 3-point schemes. It is clearfrom Table 1 and Fig. 3 that the error bounds of the 3-point schemes (13) at each subdivisionlevel decrease by increasing the arity of the schemes. Moreover, the support, computationalcost and error bounds of higher arity schemes are better than the lower arity schemes. TABLE 1: ERROR BOUNDS OF 3-POINT SCHEME WITH VARYING ARITY: k/a1 23 45 binary0.075000 0.0375000.018750 0.0093750.004687 ternary 0.033333 0.011111 0.003704 0.001235 0.000412 quaternary 0.020833 0.005208 0.001302 0.000326 0.000081 Figure 3: Comparison: Error bounds between the ݇-th level control polygons and the limitcurves of 3-point schemes of varying arity. 4. Effects of parameters in proposed We will discuss the three major effects/upshots of parameter in schemes (13). Effects ofparameters in other schemes can be discussed analogously. D. Continuity 50 Cop y ri g ht © 2012 SciRes. 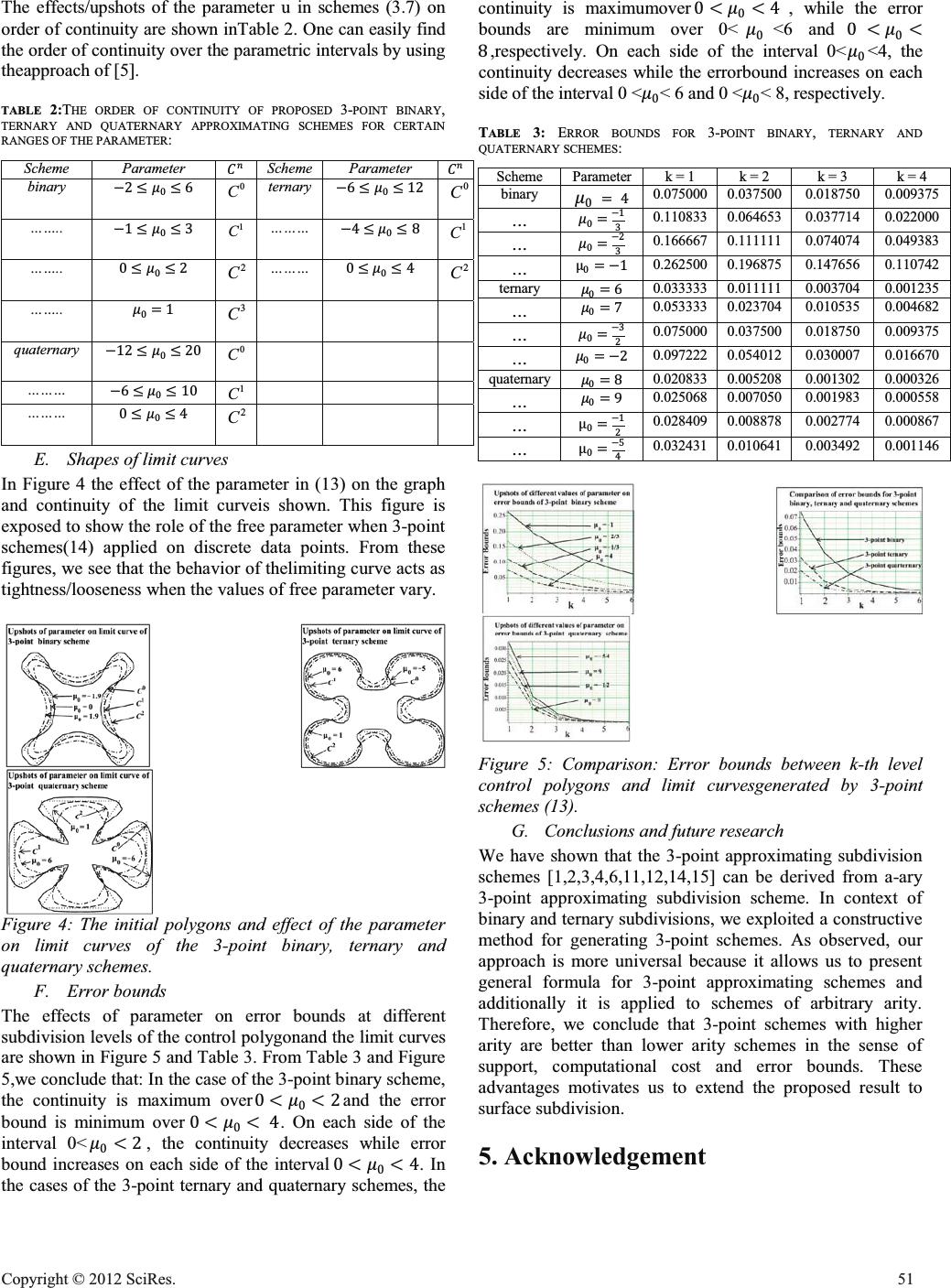 The effects/upshots of the parameter u in schemes (3.7) on order of continuity are shown inTable 2. One can easily find the order of continuity over the parametric intervals by using theapproach of [5]. TABLE 2:THE ORDER OF CONTINUITY OF PROPOSED 3-POINT BINARY, TERNARY AND QUATERNARY APPROXIMATING SCHEMES FOR CERTAIN RANGES OF THE PARAMETER: SchemeParameter ܥ݊Scheme Parameter ܥ݊ binary െ2ߤ06 0 Cternary െ6ߤ012 0 C …….. െ1ߤ03 1 C ……… െ4ߤ08 1 C …….. 0ߤ02 2 C……… 0ߤ04 2 C …….. ߤ0=1 3 C quaternary െ12ߤ020 0 C ……… െ6ߤ010 1 C ……… 0ߤ04 2 C E.Shapes of limit curves In Figure 4 the effect of the parameter in (13) on the graph and continuity of the limit curveis shown. This figure is exposed to show the role of the free parameter when 3-point schemes(14) applied on discrete data points. From these figures, we see that the behavior of thelimiting curve acts as tightness/looseness when the values of free parameter vary. Figure 4: The initial polygons and effect of the parameter on limit curves of the 3-point binary, ternary and quaternary schemes. F.Error bounds The effects of parameter on error bounds at different subdivision levels of the control polygonand the limit curves are shown in Figure 5 and Table 3. From Table 3 and Figure 5,we conclude that: In the case of the 3-point binary scheme, the continuity is maximum over0<ߤ0<2and the error bound is minimum over 0<ߤ0< 4. On each side of the interval 0<ߤ0<2, the continuity decreases while error bound increases on each side of the interval 0<ߤ0<4. In the cases of the 3-point ternary and quaternary schemes, the continuity is maximumover0<ߤ0<4 , while the error bounds are minimum over 0<ߤ0<6 and 0 <ߤ0< 8,respectively. On each side of the interval 0<ߤ0<4, the continuity decreases while the errorbound increases on each side of the interval 0 <ߤ0< 6 and 0 <ߤ0< 8, respectively. TABLE 3:ERROR BOUNDS FOR 3-POINT BINARY, TERNARY AND QUATERNARY SCHEMES: Scheme Parameter k = 1 k = 2 k = 3 k = 4 binary ߤ0 = 4 0.075000 0.037500 0.018750 0.009375 ... ߤ0=െ1 3 0.110833 0.064653 0.037714 0.022000 ... ߤ0=െ2 3 0.166667 0.111111 0.074074 0.049383 ... Ɋ0=െ1 0.262500 0.196875 0.147656 0.110742 ternary ߤ0=6 0.033333 0.011111 0.003704 0.001235 ... ߤ0=7 0.053333 0.023704 0.010535 0.004682 ... ߤ0=െ3 2 0.075000 0.037500 0.018750 0.009375 ... ߤ0=െ2 0.097222 0.054012 0.030007 0.016670 quaternary ߤ0=8 0.020833 0.005208 0.001302 0.000326 ... ߤ0=9 0.025068 0.007050 0.001983 0.000558 ... Ɋ0=െ1 2 0.028409 0.008878 0.002774 0.000867 ... Ɋ0=െ5 4 0.032431 0.010641 0.003492 0.001146 Figure 5: Comparison: Error bounds between k-th level control polygons and limit curvesgenerated by 3-point schemes (13). G.Conclusions and future research We have shown that the 3-point approximating subdivision schemes [1,2,3,4,6,11,12,14,15] can be derived from a-ary 3-point approximating subdivision scheme. In context of binary and ternary subdivisions, we exploited a constructive method for generating 3-point schemes. As observed, our approach is more universal because it allows us to present general formula for 3-point approximating schemes and additionally it is applied to schemes of arbitrary arity. Therefore, we conclude that 3-point schemes with higher arity are better than lower arity schemes in the sense of support, computational cost and error bounds. These advantages motivates us to extend the proposed result to surface subdivision. 5. Acknowledgement Cop y ri g ht © 2012 SciRes.51  This work is supported bytheBeijing Municipal Natural Science Foundation(4102027), theNational Natural Science Foundation of China (60973101) and HEC, Pakistan. REFERENCES [1] M. Aslam, G. Mustafa, and A. Ghaffar, “(2n1)-point ternary approximating and interpolatingsubdivision schemes,” Journal of Applied Mathematics, Article ID 832630, 12 pages,2011. [2] G. M. Chaikin, “An algorithm for high-speed curve generation, Computer Graphics andImage Processing,”vol. 3, 1974, pp. 346-349. [3] S. Daniel and P. Shunmugaraj, “Three point stationary and non-stationary subdivisionschemes,” 3rd International Conference on Geometric Modeling & Imaging,DOI:10.1109/GMAI.2008.13 [4] M. F. Hassan and N. A. Dodgson, “Ternary and three- point univariate subdivision schemes,” in:A. Cohen, J. L. Marrien, L. L. Schumaker (Eds.), Curve and Surface Fitting: Sant-Malo2002, Nashboro Press, Brentwood, pp. 199-208, 2003. [5] M. F. Hassan, I. P.Ivrissimitzis, N. A. Dodgson,and M. A. Sabin, “An interpolating4-point ternary stationary subdivision scheme,” Computer Aided Geometric Design,vol. 19, pp.1-18, 2002. [6] K. Hormann and M. A. Sabin, “A family of subdivision schemes with cubic precision,” ComputerAided Geometric Design, vol.25, 2008,pp. 41-52. [7] F. Khan, G. Mustafa, “A new 4-point quaternary approximating subdivision scheme,”Abstractand Applied Analysis, doi:10.1155/2009/301967 (2009). [8] J.-A. Lian, “On a-ary subdivision for curve design: III. 2mെ point and (2m + 1)െpoint interpolatoryschemes,” Applications and Applied Mathematics: An International Journal, vol. 4(2),2009, pp. 434-444. [9] J.-A. Lian, “On a-ary subdivision for curve design: I. 4- point and 6-point interpolatoryschemes,” Applications and Applied Mathematics: An International Journal, vol. 3(1), 2008, pp.18-29. [10] J.-A. Lian, “On a-ary subdivision for curve design: II. 3- point and 5-point interpolatoryschemes,” Applications and Applied Mathematics: An International Journal, vol. 3(2), 2008, pp. 176-187. [11] G. Mustafa, F. Khan and A. Ghaffar, The m-point approximating subdivision scheme,Lobachevskii Journal of Mathematics, vol. 30(2), 2009, pp. 138-145. [12] G. Mustafa, A. Ghaffar and F. Khan, “The Odd-Point Ternary Approximating Schemes,”American Journal of Computational Mathematics, vol. 1(2), pp. 111-118, 2011. doi: 10.4236/ajcm.2011.12011 [13] G. Mustafa & M. S. Hashmi, Subdivision depth computation for n-ary subdivisioncurves/surfaces, Vis Comput, vol. 26, , 2010, pp. 841-851. [14] S. S. Siddiqi and N. Ahmad, A new three point approximating C2 subdivision scheme,Applied Mathematics Letters, vol. 20, 2007, pp. 707-711. [15] S. S. Siddiqi and Rehan, K, Modified form of binary and ternary 3-point subdivisionscheme, Applied Mathematics and Computation, vol. 216, 2010, pp. 970- 982. 52 Cop y ri g ht © 2012 SciRes. |

