On Efficient Monitoring of Process Dispersion
using Interquartile Range
Shabbir Ahmad1, Zhengyan Lin1, Saddam Akber Abbasi2, Muhammad Riaz3,4
1 Department of Mathematics, Institute of Statistics, Zhejiang University, 310027, Hangzhou, China
2Department of Statistics, University of Auckland, New Zealand
3 Department of Statistics, Quaid-i-Azam University, Islamabad Pakistan
4 Department of Mathematics and Statistics, King Fahd University of Petroleum and Minerals,
Dhahran, 31261, Saudi Arabia
Abstract: The presence of dispersion/variability in any process is understood and its careful monitoring may furnish the
performance of any process. The interquartile range (IQR) is one of the dispersion measures based on lower and upper
quartiles. For efficient monitoring of process dispersion, we have proposed auxiliary information based Shewhart-type IQR
control charts (namely IQRr and IQRp charts) based on ratio and product estimators of lower and upper quartiles under
bivariate normally distributed process. We have developed the control structures of proposed charts and compared their
performances with the usual IQR chart in terms of detection ability of shift in process dispersion. For the said purpose power
curves are constructed to demonstrate the performance of the three IQR charts under discussion in this article. We have also
provided an illustrative example to justify theory and finally closed with concluding remarks.
Keywords:Auxiliary Information, Bivariate Normal Distribution, Control Carts, Interquartile Range, Lower and Upper
Quartiles, Power Curves.
1. Introduction
Statistical Process Control (SPC) is a collection of
fundamental tools which are used to monitor process
behavior. In the early 1920s Walter A. Shewhart developed
control charting as a useful tool of Statistical Process
Control (SPC) to monitor process parameters such as
location, dispersion etc. The existence of variability is
unavoidable in any process and its careful monitoring is
necessary to improve the performance of any process. The
variability in a process can be classified in two parts namely
natural and unnatural. Natural/normal variation has a
consistent pattern while unnatural/unusual variation has an
unpredictable behavior over the time. The presence of
natural variation in a process ensures that the process is in-
control state, otherwise out-of-control. Control charts assist
differentiating between natural and unnatural variations and
hence declaring the process to be in-control or out-of-
control.
To monitor process variability [1] proposed usual range
and standard deviation charts (namely R and S charts). The
efficiency of R chart is affected with the increment in
sample size where as the performance of S chart becomes
poor due to existence of outliers in data (cf. [2]). Later on
different estimators of interquartile range (IQR) have been
used to establish design structures of dispersion charts such
as: [3] and [4] have used interquartile range by restricting
the position of lower and upper quartiles as integer, which
become cause of some uneven patterns in design structure
of control chart. Rocke [5] proposed IQR based Rq chart
which out performs the R chart for detecting shifts in
process dispersion in outlier scenario. To avoid some
irregularities of Rq chart, [2] proposed a new method of
usual IQR chart based on the definition of [6]. Abbasi &
Miller [7] compared the performances of different
dispersion charts under normally and non-normally
distributed environments and concluded that for small
sample size the IQR chart exhibits reasonable performance
while the performances of R and S charts are significantly
influenced for highly skewed process environments. Much
of the work related to dispersion control charts may be seen
in the bibliographies of the above authors.
In this article we have proposed IQR control charts
namely IQRr and IQRp charts to monitor the process
dispersion in Shewhart setup. These charts are based on
ratio and product estimators of lower and upper quartiles of
study variable Y using one auxiliary variable X under
bivariate normally distributed process. The rest of the article
is organized as: Section II provides the design structure of
IQR charts based on different quantile estimators considered
here. In Section III the performance of IQR charts are
investigated under the assumption of normality. An
illustrative example is provided in Section IV to justify our
proposal and finally the study is concluded with some
recommendation in Section V.
2. Quantile Estimators andIQR
Charting Structures
Let the quality characteristic of interest is Y (e.g. inner
diameter of shaft) and X be an auxiliary characteristic (e.g.
Open Journal of Applied Sciences
Supplement：2012 world Congress on Engineering and Technology
Cop
y
ri
g
ht © 2012 SciRes.39

outside diameter) associated with Y. Let
() & ()
yx
QQ
EE
be the
E
-quantile of Y & X respectively
and
() & () ()()
yy xx
fQ fQ EE
be the values of density function at
() & ()
yx
QQ EE
respectively which can also be obtained by
the kernel method or the kth nearest neighbor (cf. [8]). Also
yx
I
be the Cramer’s coefficient defined as:
2
11 (, )(1)
()()
yx
Pxy EEE I  where E lies between 0 and 1
depending upon the choice of quantile;
11
() & () (, )) (
xy
XQ YQ Pxy P EE dd (cf. [9]).
Let
& (1,2,,)
ii
yxi n ! be a sample of size n to get
estimated values of quantile E  of Y & X
as
ව
() & ()
yx
QQ EE
respectively. We consider three
estimators of ()
y
Q E
, one usual and two based on an
auxiliary characteristic X (using ratio and product patterns)
defined as:
>@
>@
ˆ
: ()()
ව
:()() () ()
ව
:()()() ()
uy
ryxx
pyxx
Usual QQ
Ratio QQQQ
Product QQQQ
EE
EEEE
EEEE
½
°
¾
°
¿
.
(1)
It is to be mentioned that we are taking ()
x
Q E to be a known
quantile of auxiliary characteristic X. For the case of
unknown ()
x
Q E
we may estimate it by applying two phase
sampling procedure (cf. [10] and [11]). The properties of the
estimators, given in (1), can be easily obtained up to first
order degree of approximation, following [10] and [12].
In our study we have considered normally distributed
process environment under bivariate setup (, )YX
with
density function given as:

2
2
, 0
<, exp 0.5(1)
,, for
<, 11
21
/[]
xy
xy xy
yx
yx yx
yx
w
fyx
VV
U
PP U
SV VU
!
f f
 °
®f fd d
°
¯
(
2)
where,
22 22
2, ()()()()()
xy yyxxx xyx
wyxy x U PVPVP PVV  
&
yx
PP
are means of Y & X respectively,
22
&
yx
VV
are
variances of Y & X respectively,
yx
V is covariance between
Y & X, and ()
xyxyx y
UVVV be the correlation coefficient
between Y & X . The bivariate normal density plot is given
as:
Based on the estimators, given in (1)
for 0.25 & 0.75 E , we define interquartile range statistic
as:
(0.75)(0.25) ( , & ) =
ii i
IQR QQiur p
.
(
3)
We may define the control charting structures based on IQRi
( , & )iur p
to monitor the dispersion parameter
y
V of
quality characteristic Y. The probability limits of IQRi based
charting structures can be described as:


with
=
with 1
Prob Limits:
iliil l
ic
iui iuu
LPLIQRFIQRIQR
CL IQR
UPLIQRF IQRIQR
D
D
d
t

°
®
°
¯
(
4) where CL, LPL and UPL refer to the Central Limit,
Lower Probability Limit and Upper Probability Limit
respectively of IQRi charts and
lu
DDD  is a pre-
specified false alarm rate which is equally divided on both
tails of the probability distribution of IQRi to define the
probability limits. It is to be mentioned that we may also
define K-sigma limits of the structures based on IQRi
( , & )iur p
following [13].
It is to be noted that a variety of sensitizing rules are
available in quality control literature which are used to
differentiate between in-control and out-of-control states of
process (cf. [14], [15], [16]). In our study we focus on first
sensitizing rule to decide about process status for the control
structures defined in (4). The first rule is defined as:
Simulate bivariate random samples (,)
ii
yx of size n
from
the probability model (2) and compute the sample statistics
IQRis for each sample. Plot the values of IQRis against the
control limits defined in (4) or the appropriately defined K-
sigma limits. By first sensitizing rule, any value of IQRi
falling outside the control limits indicates an out-of control
signal for the dispersion parameter of quality characteristic
Y.
3. Power Study of IQR Charts
To quantify the efficiency of a design structure, the
discriminatory power is very famous performance measure
in control charting setups. In this section we have evaluated
the efficiency of IQRi charts under investigation in terms of
detection ability for shifts in process dispersion parameter
and created power curves following [17], [7] and [18]. The
in-control value of
y
V
is considered as
0
y
V
while the out-of-
control value is considered as
1
y
V
which can be defined in
terms of O
and
y
V
as
10
yy
VOV
, where
O
is amount of shift
in process dispersion
y
V . It is generally desired that for in-
control state of process the false alarm rate should be
low/close to pre-fixed value of D while for out-of-control
40 Cop
y
ri
g
ht © 2012 SciRes.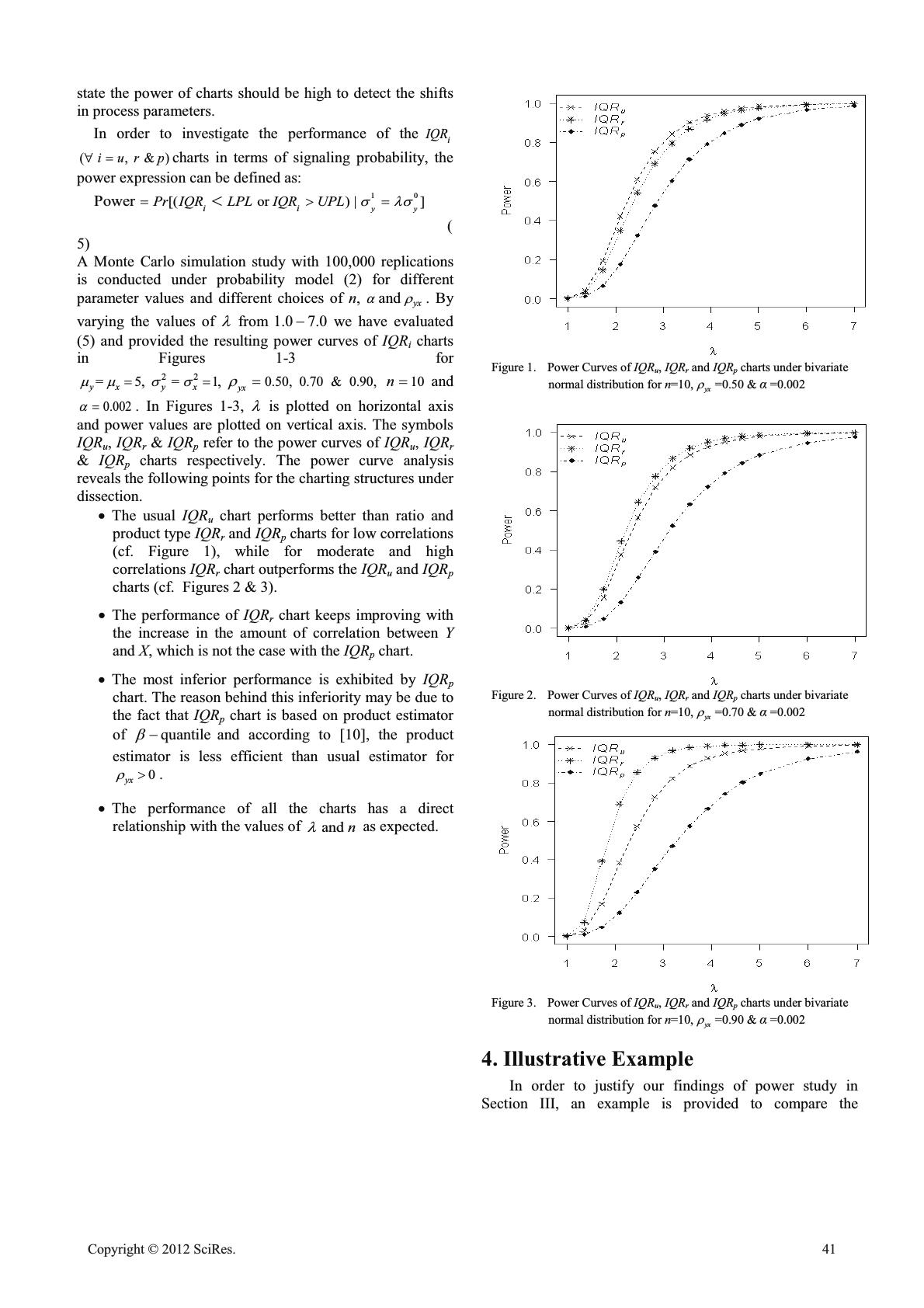

state the power of charts should be high to detect the shifts
in process parameters.
In order to investigate the performance of the
i
IQR
( , & )iur p
charts in terms of signaling probability, the
power expression can be defined as:
10
[( or ) |]Power
yy ii
Pr IQRLPLIQRUPL VOV ! 
(
5)
A Monte Carlo simulation study with 100,000 replications
is conducted under probability model (2) for different
parameter values and different choices of n, D
and
yx
U
. By
varying the values of O from 1.0 7.0 we have evaluated
(5) and provided the resulting power curves of IQRi charts
in Figures 1-3 for
22
= 5 = 1, ,
yxy x
PPV V 0.50, 0.70 & 0.90,
yx
U 10n and
0.002 D
. In Figures 1-3,
O
is plotted on horizontal axis
and power values are plotted on vertical axis. The symbols
IQRu, IQRr & IQRp refer to the power curves of IQRu, IQRr
& IQRp charts respectively. The power curve analysis
reveals the following points for the charting structures under
dissection.
xThe usual IQRu chart performs better than ratio and
product type IQRr and IQRp charts for low correlations
(cf. Figure 1), while for moderate and high
correlations IQRr chart outperforms the IQRu and IQRp
charts (cf. Figures 2 & 3).
xThe performance of IQRr chart keeps improving with
the increase in the amount of correlation between Y
and X, which is not the case with the IQRp chart.
xThe most inferior performance is exhibited by IQRp
chart. The reason behind this inferiority may be due to
the fact that IQRp chart is based on product estimator
of quantile E  and according to [10], the product
estimator is less efficient than usual estimator for
0
yx
U ! .
xThe performance of all the charts has a direct
relationship with the values of and n O
as expected.
Figure 1. Power Curves of IQRu, IQRr and IQRp charts under bivariate
normal distribution for n=10,
yx
U =0.50 & Į =0.002
Figure 2. Power Curves of IQRu, IQRr and IQRp charts under bivariate
normal distribution for n=10,
yx
U =0.70 & Į =0.002
Figure 3. Power Curves of IQRu, IQRr and IQRp charts under bivariate
normal distribution for n=10,
yx
U =0.90 & Į =0.002
4. Illustrative Example
In order to justify our findings of power study in
Section III, an example is provided to compare the
Cop
y
ri
g
ht © 2012 SciRes.41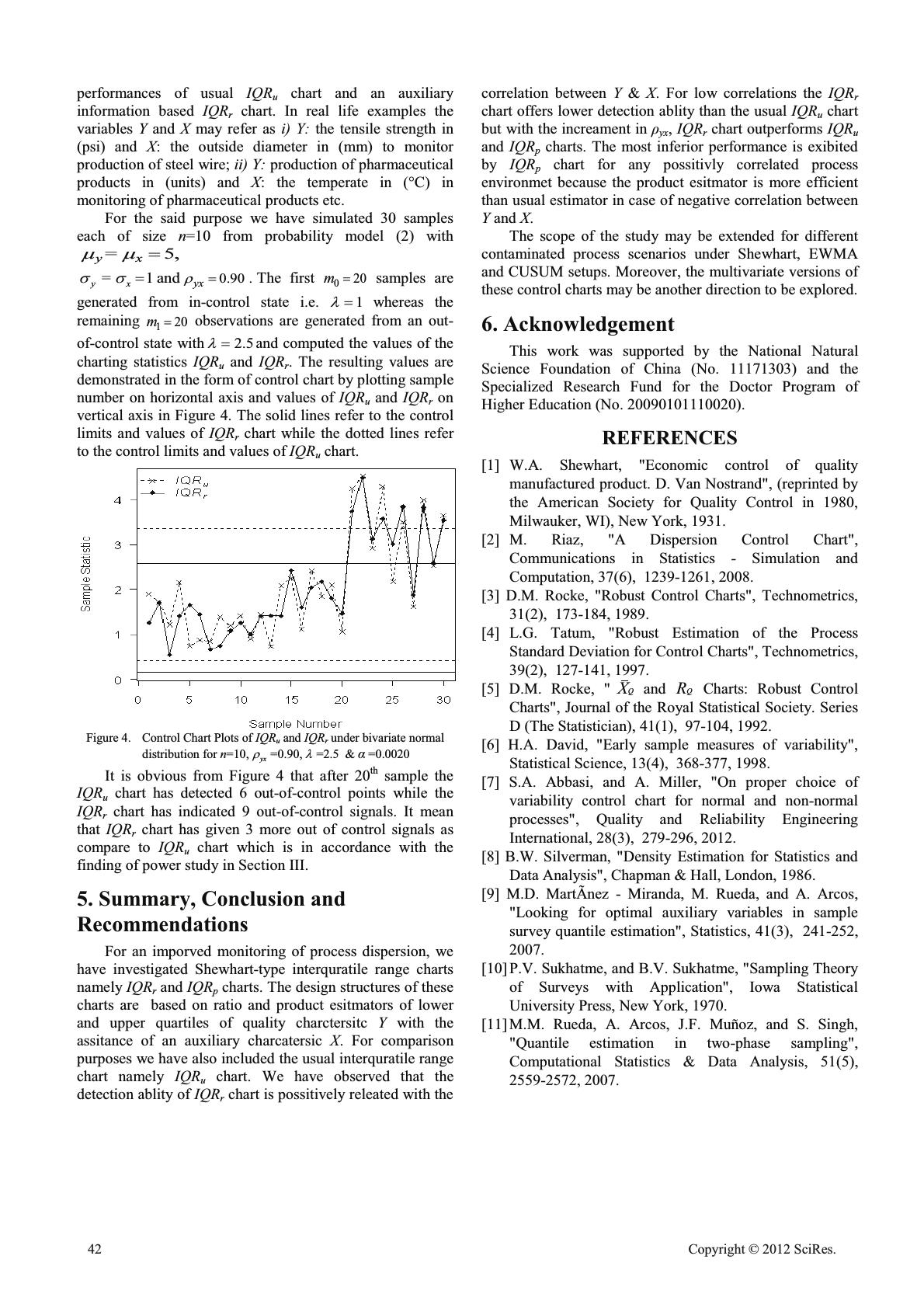

performances of usual IQRuchart and an auxiliary
information based IQRr chart. In real life examples the
variables Y and X may refer as i) Y: the tensile strength in
(psi) and X: the outside diameter in (mm) to monitor
production of steel wire; ii) Y: production of pharmaceutical
products in (units) and X: the temperate in (°C) in
monitoring of pharmaceutical products etc.
For the said purpose we have simulated 30 samples
each of size n=10 from probability model (2) with
= 5,
yx
PP
0.90 . = 1 and
yx yx
U VV
The first
0
20 m samples are
generated from in-control state i.e. 1 O whereas the
remaining
1
20m
observations are generated from an out-
of-control state with 2.5 O
and computed the values of the
charting statisticsIQRuand IQRr. The resulting values are
demonstrated in the form of control chart by plotting sample
number on horizontal axis and values of IQRuandIQRr on
vertical axis in Figure 4. The solid lines refer to the control
limits and values of IQRr chart while the dotted lines refer
to the control limits and values of IQRu chart.
Figure 4. Control Chart Plots of IQRu and IQRr under bivariate normal
distribution for n=10,
yx
U
=0.90,
O
=2.5 & Į =0.0020
It is obvious from Figure 4 that after 20th sample the
IQRu chart has detected 6 out-of-control points while the
IQRr chart has indicated 9 out-of-control signals. It mean
that IQRr chart has given 3 more out of control signals as
compare to IQRu chart which is in accordance with the
finding of power study in Section III.
5. Summary, Conclusion and
Recommendations
For an imporved monitoring of process dispersion, we
have investigated Shewhart-type interquratile range charts
namely IQRr and IQRp charts. The design structures of these
charts are based on ratio and product esitmators of lower
and upper quartiles of quality charctersitc Y with the
assitance of an auxiliary charcatersic X. For comparison
purposes we have also included the usual interquratile range
chart namely IQRu chart. We have observed that the
detection ablity of IQRr chart is possitively releated with the
correlation between Y & X. For low correlations the IQRr
chart offers lower detection ablity than the usual IQRu chart
but with the increament in ȡyx, IQRr chart outperforms IQRu
and IQRp charts. The most inferior performance is exibited
by IQRp chart for any possitivly correlated process
environmet because the product esitmator is more efficient
than usual estimator in case of negative correlation between
Y and X.
The scope of the study may be extended for different
contaminated process scenarios under Shewhart, EWMA
and CUSUM setups. Moreover, the multivariate versions of
these control charts may be another direction to be explored.
6. Acknowledgement
This work was supported by the National Natural
Science Foundation of China (No. 11171303) and the
Specialized Research Fund for the Doctor Program of
Higher Education (No. 20090101110020).
REFERENCES
[1] W.A. Shewhart, "Economic control of quality
manufactured product. D. Van Nostrand", (reprinted by
the American Society for Quality Control in 1980,
Milwauker, WI), New York, 1931.
[2] M. Riaz, "A Dispersion Control Chart",
Communications in Statistics - Simulation and
Computation, 37(6), 1239-1261, 2008.
[3] D.M. Rocke, "Robust Control Charts", Technometrics,
31(2), 173-184, 1989.
[4] L.G. Tatum, "Robust Estimation of the Process
Standard Deviation for Control Charts", Technometrics,
39(2), 127-141, 1997.
[5] D.M. Rocke, "QX and Q R
Charts: Robust Control
Charts", Journal of the Royal Statistical Society. Series
D (The Statistician), 41(1), 97-104, 1992.
[6] H.A. David, "Early sample measures of variability",
Statistical Science, 13(4), 368-377, 1998.
[7] S.A. Abbasi, and A. Miller, "On proper choice of
variability control chart for normal and non-normal
processes", Quality and Reliability Engineering
International, 28(3), 279-296, 2012.
[8] B.W. Silverman, "Density Estimation for Statistics and
Data Analysis", Chapman & Hall, London, 1986.
[9] M.D. MartÃnez - Miranda, M. Rueda, and A. Arcos,
"Looking for optimal auxiliary variables in sample
survey quantile estimation", Statistics, 41(3), 241-252,
2007.
[10] P.V. Sukhatme, and B.V. Sukhatme, "Sampling Theory
of Surveys with Application", Iowa Statistical
University Press, New York, 1970.
[11] M.M. Rueda, A. Arcos, J.F. Muñoz, and S. Singh,
"Quantile estimation in two-phase sampling",
Computational Statistics & Data Analysis, 51(5),
2559-2572, 2007.
42 Cop
y
ri
g
ht © 2012 SciRes.

[12] M.M. Rueda, A. Arcos, and M.D. Martínez,
"Difference Etimators of Quantiles in Finite
Populations", TEST, 12(2), 481-496, 2003.
[13] D.C. Montgomery, "Introduction to Statistical Quality
Control", 6, Wiley, New York, 2009.
[14] R.J.M.M. Does, and B.F. Schriever, "Variables control
chart limits and tests for special causes", Statistica
Neerlandica, 46(4), 229-245, 1992.
[15] M.B.C. Khoo, "Designs of runs rules schemes", Quality
Engineering, 17, 27-43, 2004.
[16] M.V. Koutras, S. Bersimis, and P.E. Maravelakis,
"Statistical process control using shewhart control chart
with supplementary Runs Rules", Methodology and
Computing in Applied Probability, 9, 207-224, 2007.
[17] M. Riaz, and A. Saghir, "A mean deviation-based
approach to monitor process variability", Journal of
Statistical Computation and Simulation, 79, 1173–
1193, 2009.
[18] A. Saghir, Z. Lin, S.A. Abbasi, and S. Ahmad, "The
Use of Probability Limits of COM–Poisson Charts and
their Applications", Quality and Reliability Engineering
International, 1-16, 2012.
Cop
y
ri
g
ht © 2012 SciRes.43