Paper Menu >>
Journal Menu >>
 Advances in Ma terials Physics and Che mist ry, 2012, 2, 49-52 doi:10.4236/ampc.2012.24B014 Published Online December 2012 (htt p://www.SciRP.org/journal/ampc) Copyright © 2012 SciRes. AMPC Low Temperature Electrical Transport in Double Layered CMR Manganite La1.2Sr1.4Ba0.4Mn2O7 Y. S. Reddy1, P. Kistaiah2, C. Vishnuvardhan Reddy2* 1Department of Physics, Chaitanya Bharathi Institute of Technology, Gandipet, Hyderabad, India 2Department of Physics, Osmania University, Hyderabad, India Email: *reddycvv@osmania.ac.in Received 2012 ABSTRACT The electrical transport behavior and magnetoresistance (MR) of a polycrystalline double layered manganite La1.2Sr1.4Ba0.4Mn2O7, synthesized by the sol-gel me th od, are investi gated in the temperat ure r ange 4 .2 K - 300 K. The sample exhibits an insulator-to-metal transition at 87 K (TIM) and the spin-glass (SG)-like behavior is observed below 50 K (TSG). The transport behavior is analyzed in the entire t emperature r ange con sideri ng three d ifferent regio ns: p aramagneti c insu lating r egion (T > TIM), ferromagnetic metallic region (TSG < T < TIM) and antiferromagnetic insulating region (T<TSG) by fitting the temperature dependent resistivity data to the equations governing the conduction process in the respective temperature regions. The results show that the conduction at T > TIM follows Mott variable range hopping (VRH) process, while the two-magnon scat tering process is evid enced at TSG < T < TIM which is suppressed with the applied magnetic field of 4 T. The low temperature conductivity data are also fitted with Mott VRH equation. The sample exhibits a large MR (≈45%) over a temperature range 5 K – 50 K and it shows ≈32% MR at 5 K with a magnetic field of 0.5 T. Keywords: Layered M anganit e; Magnetor esistance; Transpo rt Behavior; Variable Range Hoppi ng; Magnon Scattering 1. Introduction The discovery of colossal magnetoresistance (CMR) in La- based double layered (DL) manganites La2-2xSr1+2xMn2O7 has provided an opportunity to explore the interaction among spin, charge and lattice in reduced di mensio ns [1 ,2]. These mat erials show large values of MR at moderate magnetic fields and proved to be promising materials for many technological appli- cations. The (La,A)3Mn2O7 (A = Sr, Ca, Ba) perovskite com- pound with layered structure consists of the MnO2 bilayers which are respectively separated by the rock-sal t-type (La,A)2 O2 layers along c-axis [3]. Because of its structural anisotropy, it is expected to present the anisotropy of physical, electrical and magnetic properties. Further, the natural array of conduct- ing ferromagnetic/non-magnetic insulating/conducting ferro- magnetic junctions present in the structure of these materials may lead to large CMR at low magnetic field, i.e., low field magnetoresistance [4]. Because of the reduced dimensionality, the balance bet ween ferr omagnetic do uble exchange ((FM -DE) and antiferromagnetic superexchange (AFM-SE) interactions between Mn ions is more subtle [5,6]. Therefore, one can ex- pect that the slight changes in the size and/or concentration of (La,A) site ions can show significant effect on bulk transport and magnetic properties. Further, the Mn-O-Mn bond angle is about 180° in the (La,A)3Mn2O7 system and is about 155–170° in (La,A)MnO3 system. The bond-length can be altered by the internal pressure, i.e., by changing the size and/or concentration of (La,A) site ions, however, the variation of the Mn-O-Mn bond-length in Mn2O7 system is different from that in MnO3 system [7,8] . Therefore, th e study of lattice e ffects on t he mag- netotransport properties in the (La,A)3Mn2O7 system might be useful in understanding the fundamentals of the CMR and its related properties. We have prepared some DL manganite samples with differ- ent doping elements (Ca2+, Ba2+) at Sr2+ site with different doping levels with an aim to increase MR and TIM (insula- tor-to-metal transition temperature) and also to investigate the transport phenomena in these materials. In this paper, we present the results obtained for La1.2Sr1.4Ba0.4Mn2O7 which exists in three different regions: paramagnetic insulating region, ferromagnetic metallic region and antiferromagnetic insulating region in the temperature range 4.2 K – 300 K with a main focus on its transport behavior. 2. Experiment High pure powders of La2O3, MnCO3, Sr(NO3)2 and Ba(NO3)2. 4H2O, in stoichiometric proportions, were used to obtain the nominal composition of La1.2Sr1.4Ba0.4Mn2O7. La2O3 and MnCO3 were converted into nitrates prior to use. All the nitrates were dissolved in the citric acid solution and then the pH was ad- justed to 6 with ammonia solution. After getting the water eva- porated from the solution, ethylene glycol was added to it and heated at about 90oC until a gel-type solution is formed. The gel was dried at 150oC and then decomposed at 250oC in air for 2 h to decompose nitrates and all organic materials. The resultant ash was ground to get a fine homogeneous powder. The powder was calcinated in air 1100oC for 10 h and then pressed into circular pellets. The pellets were finally sintered in air at 1400oC for 6 h. The structural characterization was carried out by X-ray d if- fraction using X- pert pro system, M /S Pananlytical (λ = 1.5405 6 *Corresponding author.  Y. S. RE DDY ET AL. Copyright © 2012 SciRes. AMPC 50 Å) in the 2θ range 20˚ - 80˚ with step size 0.01˚ and a count time of 0.6 s per step. The results of powder X-ray diffraction suggest the formation of single phase with body-centered te- tragonal structure (space group: I4/mmm). The electrical resis- tivity at different applied magnetic fields (H = 0 T, 1.5 T and 4 T) is measured by standard four-probe method over the temper- ature range 4.2 K–300 K with the use of a superconducting magnet system of Oxford. 3. Results and Discussion The temperature (T) dependent electrical resistivity (ρ) of the sample at different magnetic fields is shown in Figure 1. As th e temperatu re i s decr eas ed fro m 3 0 0 K, th e resis tivity of th e sam- ple in creases and reach es maximum at 87 K whi ch is known as insulator-to-metal transition temperature (TIM). As the temper- ature is further lowered from TIM, an upturn of resistivity is obser ved at ≈50 K which is termed as spin-glass (S G)-like tran- sition temperature (TSG) [7,8]. The SG-like behavior is attri- buted to the competing intra-bilayer FM-DE and inter-bilayer AFM-SE interactions which usually coexist in quasi 2D bilayer manganites and become dominant at low temperatures. When magnetic field is applied, TIM shifts to higher temperatures whereas SG-like transition region gets broadened due to the suppression of magnetic fluctuations with the applied magnetic field. The sample exists in three different states at different tem- peratures and hence to explain the nature of conduction me- chanism of the sample, the temperature dependent electrical resistivity data are analyzed in the in the entire temperature range (4.2 K - 300 K) in three different temperature regions: (i) paramagnetic (PM) insulating region (T>TIM), (ii) ferromag- netic (FM) metallic region (TSG<T<TIM) and (iii) antiferroma- gentic (AFM) insulating region (T<TSG). 3.1. Conduction Mechanism at T > TIM The conduction mechanism in PM semiconducting/insulating region in manganites is usually explained by four models: They are: (i) semiconduction (SC) model described by Arrhenius equation ρ = ρ0exp(Ea/kBT) [9], (ii) nearest neighbor small po- laron hopping (SPH) model described by ρ = ρ0Tnexp(Ep/kBT), Figure 1. Temperature dependent Electrical resistivity and MR plots of La1.2Sr1.4Ba0.4Mn2O7. where n = 1 for adiabatic hopping [10] and n = 1.5 for non- adiabatic hopping [11], (iii) Mott type of VRH model described by ρ = ρ∞Tnexp(T0/T)p, where p = 1/(d+1), d being the dimen- sionality of the system [12,13] and (iv) Efros-Shkloskii (ES) type of VRH model described by [14]. The value of characte- ristic temperature (T0) in Mott VRH model is given by 24/π LdkBN(EF), where L is localization length of trapped charge carriers (here, L = 10-10 m), N(EF) is density of the localized states at Fermi level and d is the dimensionality of the system. The Coulomb interaction in hopping regime which produces a gap in electronic density of states (DOS) is responsible for ES VRH type o f con du cti on mechan i s m, whereas M ot t V RH ar ises when such gap is filled. Each model predicts a different tem- perature dependence of the resistivity and fits the resistivity data in different temperature r anges. In the present study, the ρ-T data are analyzed by fitting the data to all the equations mentioned above. The ρ-T data do not fit well to the equations of SC and SPH models; ES VRH gives reasonably good fittings, but the best fittings are obtained with Mott VRH model over a wide temperature range (Figure 2). The Mott 2D and 3D VRH models give almost indistinguisha- ble fittings for drawing any conclusion about dimensionality dependence, however, the results clearly point towards Mott type of VRH conduction mechanism in PM insulating region (T> TIM). The best fit parameters obtained with Mott 2D and 3D VRH models are listed in Table 1 and they are in good agree- ment with the previous reports on similar DL manganites [15,1 6]. The d ecreas e i n t he valu es o f T0 and the in crease i n t he values of N(EF) with the magnetic field is due to the suppres- sion of magnetic domain scattering with applied magnetic field. Figure 2. Plots of ln ρ - T-1/4 and ln ρ - T-1/3 for La1.2Sr1.4Ba0.4Mn2O7. The solid line s give the best fits to Mott 2D and 3D VRH models. Table 1. The best fit parametres obtaine d from mott 2d and 3d vrh model fittin gs. H (T) Mott 3D VRH Mott 2D VRH ρ0 (Ω cm) T0 (K) N(EF) (eV-1cm-3) ρ0 (Ω cm) T0 (K) N(EF) (eV-1cm-2) 0 4 8.3×10-5 4.5×10 -4 1.6×107 1.0×107 5.4×1021 8.8×1021 4.7×10-3 1.5×10-2 4.3×105 3.0×105 2.1×1015 2.9×1015 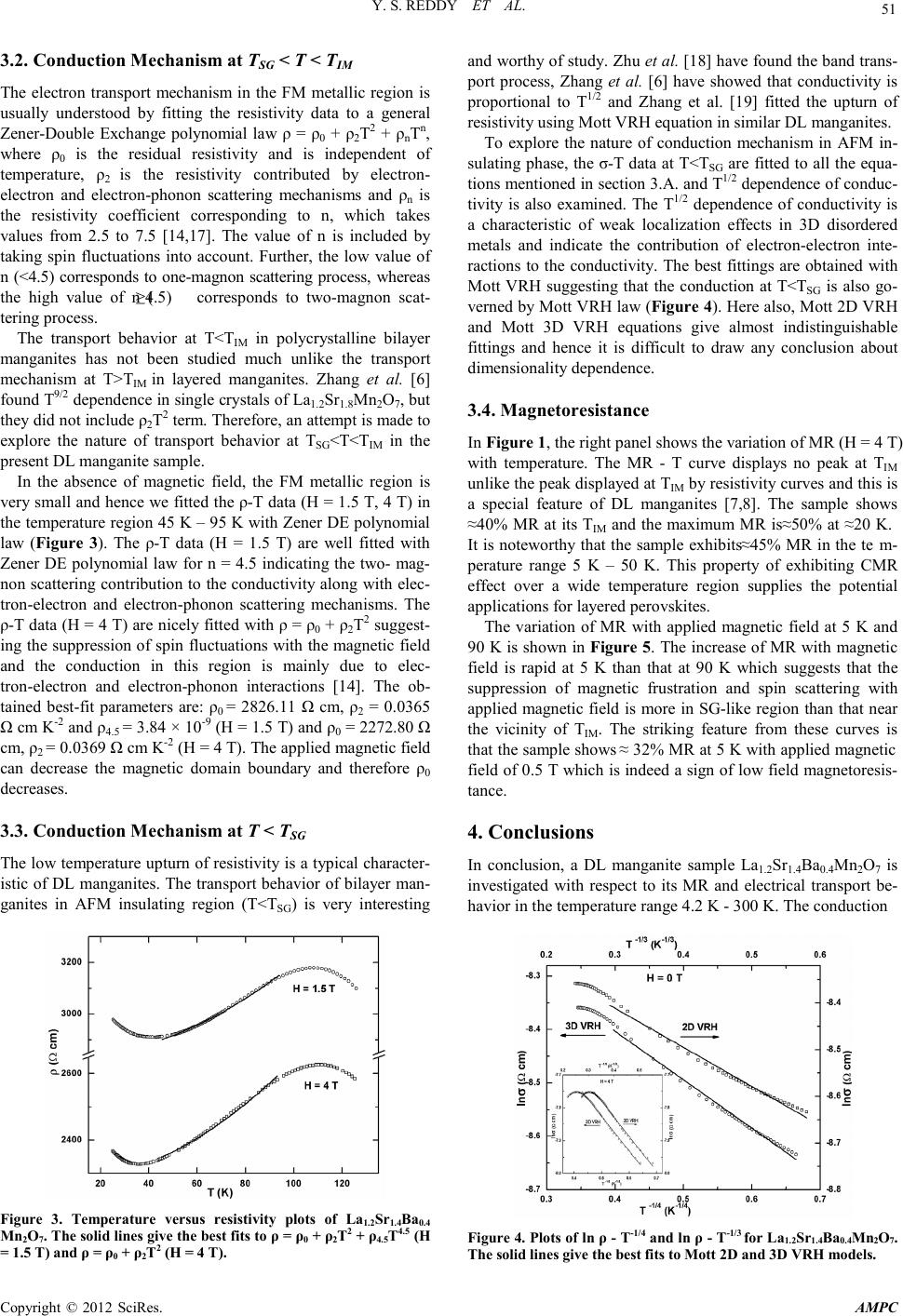 Y. S. REDDY ET AL. Copyright © 2012 SciRes. AM PC 51 3.2. Conduction Mechanism at TSG < T < TIM The electron transport mechanism in the FM metallic region is usually understood by fitting the resistivity data to a general Zener-Double Exchange polynomial law ρ = ρ0 + ρ2T2 + ρnTn, where ρ0 is the residual resistivity and is independent of temperature, ρ2 is the resistivity contributed by electron- electron and electron-phonon scattering mechanisms and ρn is the resistivity coefficient corresponding to n, which takes values from 2.5 to 7.5 [14,17]. The value of n is included by taking spin fluctuations into account. Further, the low value of n (<4.5) corresponds to one-magnon scattering process, wherea s the high value of n (≥4.5) corresponds to two-magnon scat- tering process. The transport behavior at T<TIM in polycrystalline bilayer manganites has not been studied much unlike the transport mechanism at T>TIM in layered manganites. Zhang et al. [6] found T9/2 depend ence in singl e crystals of La1.2Sr1.8Mn2O7, bu t they did not include ρ2T2 term. Therefore, an att empt is made to explore the nature of transport behavior at TSG<T<TIM in the presen t DL manganite s ample. In the absence of magnetic field, the FM metallic region is very small an d hence we fitted the ρ-T data (H = 1.5 T, 4 T) in the temperat ure region 45 K – 95 K with Zener DE polynomial law (Figure 3). The ρ-T data (H = 1.5 T) are well fitted with Zener DE polynomial law for n = 4.5 indicating the two- mag- non scattering contribution to the conductivity along with elec- tron-electron and electron-phonon scattering mechanisms. The ρ-T data (H = 4 T) are nicely fitted with ρ = ρ0 + ρ2T2 suggest- ing the suppression of spin fluctuations with the magnetic field and the conduction in this region is mainly due to elec- tron-electron and electron-phonon interactions [14]. The ob- tained best-fit parameters are: ρ0 = 2826.11 Ω cm, ρ2 = 0.0365 Ω cm K-2 and ρ4.5 = 3.84 × 10-9 (H = 1.5 T) and ρ0 = 2272.80 Ω cm, ρ2 = 0.0369 Ω cm K-2 (H = 4 T). The ap p lied magnetic field can decrease the magnetic domain boundary and therefore ρ0 decreases. 3.3. Conduction Mechanism at T < TSG The low te mper ature up turn of resisti vity is a typical character- istic of DL manganites. Th e transpo rt beh avior of bilayer man- ganites in AFM insulating region (T<TSG) is very interesting Figure 3. Temperature versus resistivity plots of La1.2Sr1.4Ba0.4 Mn2O7. The solid lines give the best fits to ρ = ρ0 + ρ2T2 + ρ4.5T4.5 (H = 1.5 T) and ρ = ρ0 + ρ2T2 (H = 4 T). and worthy of study. Zhu et al. [18] have found the band trans- port process, Zhang et al. [6] have showed that conductivity is proportional to T1/2 and Zhang et al. [19] fitted the upturn of resistivity using Mott VRH equation in similar DL manganites. To explore the nature of conduction mechanism in AFM in- sulating phase, the σ-T data at T <TSG are fitted to all the equa- tions mentioned in section 3.A. and T1/2 dependence of conduc- tivity is also examined. The T1/2 dependence of conductivity is a characteristic of weak localization effects in 3D disordered metals and indicate the contribution of electron-electron inte- ractions to the conductivity. The best fittings are obtained with Mott VRH suggesting that the conduction at T<TSG is also go- verned by Mott VRH law (Figure 4). Here also , Mot t 2D VRH and Mott 3D VRH equations give almost indistinguishable fittings and hence it is difficult to draw any conclusion about dimensionality dependence. 3.4. Magnetoresistance In Figure 1, the right panel shows the variation of MR (H = 4 T) with temperature. The MR - T curve displays no peak at TIM unl ike th e peak d isp layed at TIM by resistivity curves and th is is a special feature of DL manganites [7,8]. The sample shows ≈40% MR at its TIM and th e maximu m MR is ≈50% at ≈20 K. It is noteworthy that the sample exhibits ≈45% MR in the tem- perature range 5 K – 50 K. This property of exhibiting CMR effect over a wide temperature region supplies the potential appl ications for layered p er ovskites. The variation of MR with applied magnetic field at 5 K and 90 K is shown in Figure 5. The increase of MR with magnet ic field is rapid at 5 K than that at 90 K which suggests that the suppression of magnetic frustration and spin scattering with applied magnetic field is more in SG-like region than that near the vicinity of TIM. The striking feature from these curves is that the sample shows ≈ 32% MR at 5 K with applied magnetic field of 0.5 T which is indeed a sign of low field magneto resis- tance. 4. Conclusions In conclusion, a DL manganite sample La1.2Sr1.4Ba0.4Mn2O7 is investigated with respect to its MR and electrical transport be- havior in the temperat ure ran ge 4.2 K - 300 K. The conduction Figure 4. Plots of ln ρ - T-1/4 and ln ρ - T-1/3 for La1.2Sr1.4Ba0.4Mn2O7. The solid line s give the best fits to Mott 2D and 3D VRH models.  Y. S. RE DDY ET AL. Copyright © 2012 SciRes. AM PC 52 Figure 5. The variation of MR with appline magnetic field for La1.2Sr1.4Ba0.4Mn2O7. proces s at T > TIM is due to Mott VRH process and the metallic conduction is contributed by electron-electron scattering and two-magnon scattering at low magnetic fields and at higher fields magnon scattering mechanism is disappeared. The con- ductivity in SG-like region is also governed by Mott VRH process. The property of exhibiting large MR over a wide tem- perature range and low field magnetoresistance are found in this sample. 5. Acknowledgements The authors are thankful to the centre director, UGC-DAE Consortium for Scientific Research, Indore, for providing expe- rimental facilities. REFERENCES [1] Y. Moritomo, A. Asamitsu, H. Kuwahara, and Y. Tokura, “Giant magnetoresistance of manganese oxides with a layered perovskite structu re”, Nature (London) , vol. 380, pp . 141-144, Marc h 1996. [2] Y. Moritomo, A. Asamitsu, H. Kuwahara, and Y. Tokura, “Giant magnetoresistance of manganese oxides with a layered perovskite structure” , Nature ( Lon don), vol. 380, pp. 141-144, Marc h 1996. [3] T. Kimura, Y.Tomioka, H. Kuwahara, A. Asamitsu, M.Tamura, and Y.Tokura, “Interplane tunneling magnetoresistance in a layered manganite crystal”, Science, vol. 274, pp. 1698 – 1701, December 1996. [4] Hong Zhu, XianMing Liu, KeQing Ruan, and YuHeng Zhang, “Magnetic inhomogeneity and variable-range hopping transport at temperatures above the ferromagnetic transition in La 1.4Sr1.6Mn2-yTiyO7 system”, Phys. Rev. B,vol. 65, pp. 104424 (1-7), February 2002. [5] E. O. Chi, Y.-U. Kwon, J.-T. Kim, and N. H. Hur, “Lattice ef- fects on the magnetic and transport properties in La 1.4Sr1.6-xAxMn2O7 (A = Ca, Ba)”, Solid State Commun., vol. 110, pp. 569, 1999. [6] S. Okamoto, S. Ishihara, and S. Maekawa, “Orbital structure and magnetic ordering in layered manganites: Universal correlation and its mechanism”, Phys. Rev. B, vol. 63, pp. 104401 (1-6), February 2001. [7] C. L. Zhang, X. J. Chen, C. C. Almasan, and J. S. Gardner, J. L. Sarrao, “Low-temperature electrical transport in bilayer manga- nite La1.2Sr1.8Mn2O7”, Phys. Rev. B, vol. 65, pp. 134439 (1-6), Marc h 2002. [8] S. Chatterjee, P. H. Chou, C. F. Chang, I. P. Hong, and H. D. Yang, “Lattice effects on the transport properties of (R,Sr)3Mn2O7 (R = La, Eu, Pr)”, Phys . Rev. B, vol. 6 1, pp. 6106 – 6113, March 2000. [9] H. Zhu, D. Zhu, and Y. Zhang, “Effect of lattice expansion on the magnetotransport properties in layered manganites La 1.4Sr1.6-yBayMn2O7”, J. Appl. Phys., vol. 92, pp. 7355 – 7361, December 2002. [10] S. B. Ogale, V. Talyansky, C. H. Chen, R. Ramesh, R. L. Green, and T. Venkatesan, “Unusual electric field effects in Nd0.7Sr0.3MnO3”, Phys. Rev. Lett., vol. 77, pp. 1159 – 1 162, Au- gust 1996. [11] G. Jeffrey Snyder, R. Hiskes, S. Dicarolis, M. R. Beasley, and T. H. Geballe, “Intrinsic electrical transport an d mag n eti c pr op erti es of La 0.67Ca0.33MnO3 a n d La0.67Sr0.33MnO3 MOCVD thin films and bulk material”, Phys. Rev. B, vol. 53, pp. 14434 – 14444, June 1996. [12] M. Jaime, H.T. Hardner, M.B. Salamon, M. Rubinstein, P. Dor- sey, and D. Emin, “Hall-effect sign anomaly and small-polaron condu cti on i n (La1-xGd x)0.67Ca0.33MnO3”, Phy. Rev. Lett., vol. 78, pp. 951-954, February 1997. [13] M. Viret, L. Ranno, and J. M. D. Coey, “Colossal magnetore- sistance of t he va riable range hoppi ng regime in the manganites”, J Appl. Phys., vol. 81, pp. 4964 – 496 6, A pr il 199 7. [14] Yu Wang a nd Jorge J. San tiago-Aviles, “Large negative magne- toresistance and strong localization in highly disordered elec- trospun pregraphitic carbon nanofiber”, Appl. Phys. Lett., vol. 89, pp. 123119 (1-3 ) , September 2006. [15] D. S. Rana, C. M. Thaker, K. R. Mavani, D. G. Kuberkar, Dar- shan C. Kundaliya, and S. K. Malik, “Magnetic and transport properties of (La0.7-2xEux)(Ca0.3Srx)Mn O3: Effect of simultaneous size disorder and carrier density”, J. Appl. Phys., vol. 95, pp. 4934 - 4940, May 2004. [16] M. Matsukawa, M. Chiba, E. Kikuchi,R. Suryanarayanan, M. Apostu, S. Nimori, K. Sugimoto, and N. Kobayashi, “Effect of suppression of local distortion on the magnetic, electrical, and thermal transport properties of the Cr-substituted bilayer manga- nite LaSr2Mn2O7”, Phys. Rev. B, vol. 72, pp. 224422 (1-8), December 2005. [17] M. H. Ehsani, P.Kameli, and M. E.Ghazi, “Influence of grain size on the electrical properties of the double-layered La Sr2Mn2O7 manganite”, J. Phys. Chem. Sol., vol. 73, pp. 744–750, 2012. [18] Aritra Banerjee, S. Pal, and B. K. Chaudhuria, “Nature of small-p olaron h oppin g c onduc ti on and the effect of C r d opin g on the transport properties of rare-earth manganite La 0.5Pb0.5Mn1-xCrxO3”, J. Chem. Phys., vol. 115, pp. 1550-1558, July 2001. [19] Hong Zhu, XiaoJun Xu, Li Pi, and YuHeng Zhang, “ Two-dimensional magnetic correlation and transport behavior of layered manganite La1.4Sr1.6Mn2-xCuxO7”. Phys. Rev. B, vol. 62, pp. 6754-6760, Septe m ber, 2000. [20] R. L. Zhang, W. H. Song, Y. Q. Ma, J. Yang, B. C. Zhao, Z. G. Shen g, J. M. Dai , and Y. P. S un, “Influence of Co doping on the charge-ord erin g sta te of the bi layered m anga nit e LaSr 2Mn2O7”, Phys. Rev. B., vol. 70, pp. 224418 (1-6), D ecember 2004. |

