Othogonal Waveform Design for Multiple-Input Multiple-
Output (MIMO) Radar
Hai Deng
Department of Electrical and Computer Engineering
Florida International University, Miami, Florida, 33174, USA
Abstract—An effective numerical approach is developed for orthogonal waveform design for Multiple-Input Multiple-Output
(MIMO) radar. The Doppler shift tolerance is considered in the design cost function. The design results indicate that the Doppler
tolerance of the designed orthogonal waveforms is markedly improved.
Keywords-MIMO radar; waveform design; Doppler effect;
1. Introduction
Multiple-Input Multiple-Output (MIMO) radar is capable to
significantly improve radar performance over traditional
phased array radar via integrating target scattering information
from multiple diversified channels [1, 2]. The key to
implementing MIMO radar is to design, to generate, and to
process a group of orthogonal coding waveforms for each of
the antenna elements [3]. Consider an MIMO radar with L
antenna elements with each of them transmitting a distinct
waveform from a group of orthogonal coding
waveforms
^` Lltu
l
,3, ,2 ,1 ),(
at the same carrier
frequency, any two coding waveforms used by the MIMO
radar are supposed to be aperiodically orthogonal, therefore,
the cross-correlation function of two orthogonal coding
waveforms
)(tu
p
and
)(tu
q
used in MIMO radar should be
close to zero. For the coding waveforms to achieve the high
range resolution, the aperiodic autocorrelation function of any
coding waveform
)(tul
in the orthogonal waveform group
should be close to the Dirac delta function. However, the
designed waveforms are not orthogonal when a Doppler shift
exists in the radar echoes due to moving targets, leading to
significant target signal loss at matched filter outputs and
possible missing target detection. Orthogonal coding
waveforms with Doppler tolerance should be designed and
used for MIMO radar in this case. Algebraic methods for
design of orthogonal waveforms with Doppler tolerance would
be desirable, but are extremely difficult to implement and
basically ineffective. Therefore, numerical optimization is the
only feasible approach to designing orthogonal waveforms
with Doppler tolerance for MIMO radar [3]. For the
application of numerical optimization approach, a cost
function must be identified and the effective numerical
optimization algorithm must be developed to minimize the
cost function.
2. Definition of Cost Function with
Doppler Shift Constraint
Consider a group of L orthogonal phase coding MIMO radar
waveforms with code length equal to N. If the phase coding
sequence for L waveforms
is },2,1,,2,1),({ LlNnnsl , the autocorrelation
function of any waveform is required to be a thumbtack-like
function as:
Ll
Nm
m
mnsns
N
msA
mN
n
lll
,...,2,1
10 ,0
0 , 1
)()(
1
),(
1
0
*
¯
®

d

¦

(1)
If the Doppler frequency exists, the autocorrelation
becomes
¦


mN
n
l
nfj
l
dlf
mnsens
N
fmsA
d
1
0
2
*
)()(
1
),,(
WS
(2)
If the Doppler frequency d fis discretized as multiple times
of a unit Doppler frequency which is based on the reciprocal of
the waveform duration T, i.e.
2 ,1 ,0,/rr ddd kTkf (3)
The function in (4) is changed to:
10 ,)()(
1
),,(
1
0
/2 *

¦


D
DS
mN
n
l
Nnkj
l
dlf
mnsens
N
kmsA
d
(4)
Open Journal of Applied Sciences
Supplement：2012 world Congress on Engineering and Technology
22 Cop
y
ri
g
ht © 2012 SciRes.

The cross-correlation function of two waveforms
qp
ss and
with Doppler shift considered is given by:
Lqpqp
mnsens
N
kmssC
mN
n
q
Nnkj
p
dqpf
d
,...,2,1 , , 0
)()(
1
),,,(
1
0
/2 *
z|

¦

 DS
(5)
The final cost function is:
¦¦¦¦
¦¦
¦¦
rr




z


¸
¸
¹
·
¨
¨
©
§

,2,1,0
1
11
1
)1(
2
2
01
2
1
1
1
1
2
),,,(
),,(max
),(
d
d
k
L
p
L
pq
N
Nm
dqpf
k
L
ldlf
m
L
l
N
m
l
kmC
kmA
N
mAC
IIO
I
O
I
(6)
where
1
O
and
2
O
are the weighting coefficients for
autocorrelation and cross-correlation functions with Doppler
frequency in the cost function. The design of orthogonal
waveforms },,,{ **
2
*
1L
sss  for MIMO radar is carried by
minimizing the cost function in (6) and the optimum
orthogonal waveforms are given by:
)(minarg},,,{
**
2
*
1
*
SsssS
S
C
L:

(7)
L phase coding waveforms.
An innovative technique termed as Enhanced Simulated
Annealing (ESA) will be implemented to optimize (7) for a set
of orthogonal phase-coding waveforms with Doppler shift
tolerance for MIMO radar.
4. Statistical Approach for Orthogonal
Waveform Design
Basic Simulated Annealing (SA) algorithm has been
successfully employed for the design of orthogonal coding
waveforms with small group sizes [4, 5]. However, we have
found SA algorithm becomes much less effective when the
problem size LN is greater than 2000, where L and N are the
orthogonal waveform group size and the code length,
respectively. For conventional SA algorithms, the random
coding perturbations are used in optimization process to
“jump” out of a local minimum to reach the global optimum.
However, with large problem sizes, when the temperature is
low, SA algorithm becomes greedier and tends to be “stuck”
in the local minima. Therefore, the basic SA algorithm is not
effective for the design of more than 100 orthogonal
waveforms as required in this project. We propose an
enhanced simulated annealing (ESA) algorithm for the design
of orthogonal waveforms with large problem sizes. In ESA,
the coding perturbations are adapted to the temperature and
cost change pattern. When the temperature is high, the coding
perturbations are minor as those in the regular SA algorithms;
when temperature is lowered, the coding perturbations are
made to be strong enough for the optimization to jump out of
the local minima. The approach is motivated by the
“tunneling” method in quantum annealing [6]. The advantage
of using ESA over basic SA algorithm is illustrated in Figure 1.
As shown in Figure 1, for optimization to jump out of a local
minimum, multiple “hill-climbing” perturbations are needed in
basic SA algorithms, but adaptive perturbation can tunnel
through “the hill” directly. Therefore, by using adaptive
frequency perturbations, the ESA optimization is more rapidly
to reach equilibrium condition and more likely to find the
global minimum in the orthogonal waveform design.
3. Design Results
ESA has been implemented for Doppler shift tolerant
orthogonal waveform design based on the cost function in (5).
The number of orthogonal coding waveforms is 3, the number
of admissible phase values for each subpulse phase coding is 8
and the code lengths are chosen to be 64 and128. In addition,
the following optimization parameters are chosen: O1=1 and
O2=0.1.
Fig. 2 shows the MIMO radar matched filtering outputs of
three designed orthogonal coding waveforms with a code
length of 64 vs. different Doppler shifts in the radar echoes. It
is found that the outputs are significantly improved with
Doppler shift existing when the Doppler shift tolerant
waveform design approach is used. Fig. 3 shows the cross-
correlation functions of orthogonal waveforms when the
Doppler shift is not zero or the matched filtering outputs for
the waveforms containing Doppler shift and matched to other
matched filters. The results indicate that the cross-correlation
outputs for the designed codes with Doppler shift considered
are slightly improved compared to those for the codes
designed without considering Doppler shift. The simulation
results indicate that ESA is very effective in designing
Doppler-tolerant orthogonal waveforms for MIMO radar.
Cop
y
ri
g
ht © 2012 SciRes.23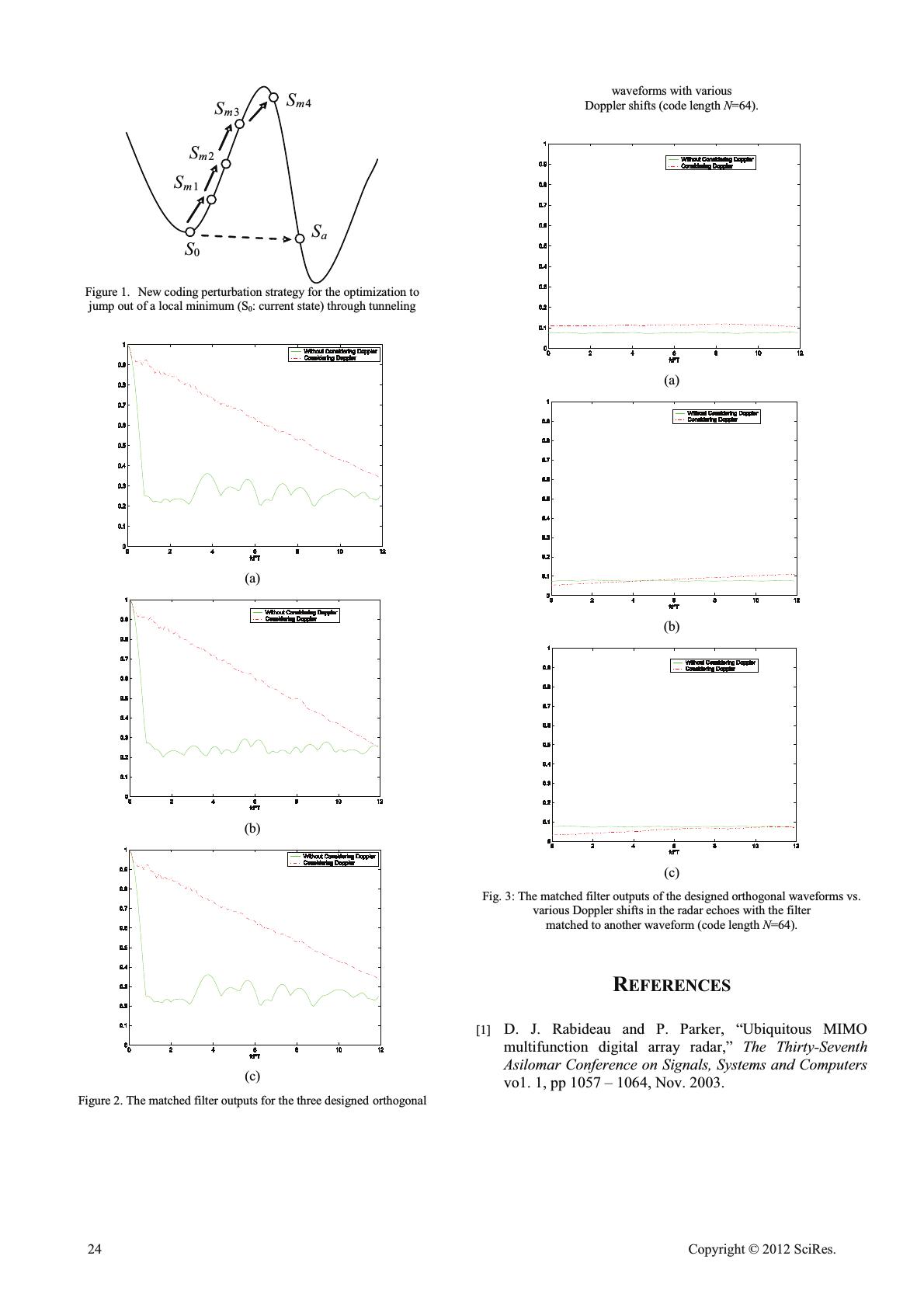

S
0
S
m1
S
a
S
m2
S
m3
S
m4
Figure 1. New coding perturbation strategy for the optimization to
jump out of a local minimum (S0: current state) through tunneling
(a)
(b)
(c)
Figure 2. The matched filter outputs for the three designed orthogonal
waveforms with various
Doppler shifts (code length N=64).
(a)
(b)
(c)
Fig. 3: The matched filter outputs of the designed orthogonal waveforms vs.
various Doppler shifts in the radar echoes with the filter
matched to another waveform (code length N=64).
REFERENCES
[1] D. J. Rabideau and P. Parker, “Ubiquitous MIMO
multifunction digital array radar,” The Thirty-Seventh
Asilomar Conference on Signals, Systems and Computers
vo1. 1, pp 1057 – 1064, Nov. 2003.
24 Cop
y
ri
g
ht © 2012 SciRes.

[2] F. C. Robey and et al, “MIMO radar theory and
experimental results,” The Thirty-Eighth Asilomar
Conference on Signals, Systems and Computers vo1. 1,
pp 300 – 304, Nov. 2004.
[3] H. Deng, “Polyphase coding signal design for orthogonal
netted radar systems,” IEEE Transactions on Signal
Processing, vol. 52, pp. 3126-3135, November 2004.
[4] S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi,
“Optimization by simulated annealing,” Science, vol. 220,
pp. 671-680, May 1983.
[5] L. Ingber, Adaptive simulated annealing (ASA): Lessons
learned, Control and Cybernetics, vol. 25, pp. 33-54, no.1,
Jan. 1996.
[6] Arnab Das and Bikas K. Chakrabarti (Eds.), Quantum
Annealing and Related Optimization Methods, Lecture
Note in Physics, vol. 679, Springer, Heidelberg, Germany,
2005.
Cop
y
ri
g
ht © 2012 SciRes.25