Statistical Theory of Turbulence by the Late Lamented Dr. Shunichi Tsugé Case Study on Flow through a Grid in Wind Tunnel

doi:10.4236/ojapps.2012.24B005

Paper Menu >>

Journal Menu >>

Statistical Theory of Turbulence

by the Late Lamented Dr. Shunichi Tsugé

Case Study on Flow through a Grid in Wind Tunnel

Takeo Nakagawa, Hiroyuki Iida

School of Information Science

Japan Advanced Institute of Science and Technology

Nomi, Japan

takeo-n@jaist.ac,jp; iida@jaist.ac.jp

Abstract—This paper is concerned with statistical theory of turbulence by the late lamented Dr. Shunichi Tsugª. The theory has

been applied to the primary flow through a grid fixed vertically with respect to the horizontal axis of the wind tunnel. The first

analytical solution has been obtained and explained the well-known “the inverse-linear decay law” of the turbulent intensity. It is

believed that the present result is the first exact solution in the theory of turbulence.

Keywords-grid-produced turbulence;exact solution;turbulent intensity;statistical theory of turbulence;applied mathematics



1. Introduction

Contrary to the firm kinetic theoretical basis of the Navier-

Stokes equation for laminar flows, which verification dates

back to Chapman[1], Enskog[2] and Grad[3], the history of its

turbulent counterpart starts in late 1960s: It is known that two

pioneering workers attempt to two-particle version of the

Euler equation(Zhigulev[4]) and of the Navier-Stokes

equatio n(T sugª=?), which are governing turbulent

correlations for inviscid and viscid gases, respectively. It is

notable that these two papers have proposed a rather striking

thesis, completely contradicting to the conventional belief that

“the kinetic theory is useless for turbulence, because it is

merely concerned with molecular fluctuations having order of

n(the mean number density), and thus are negligibly small

compared with macroscopic turbulent fluctuations of order of

n2”. In fact, human sensors are unable to perceive molecular

fluctuations, consisting of thermal agitation such as molecular

stress and heat-flux fluctuations, as discussed by Landau &

Lifshitz[6], together with fluctuations due to real-gas effects.

An independent innovative hypothesis is proposed by

Tsugª[7] and Grad[8] has made us possible to incorporate

macroscopic turbulent fluctuations into the regime of the

kinetic theory. That is, the two-particle molecular chaos due

to Boltzman is replaced with a less stringent tertiary molecular

chaos. This milder hypothesis leads us to a new finding that in

a shear flow, turbulent correlations are survived over thousand

mean free paths, or a macroscopic fluid-dynamic length, being

detectable with any flow device used currently.

In 1974, it is shown by Tsugª [7]that the equations

governing two-point correlations in an incompressible shear

flow are separable into two Orr-Sommerfeld type equations at

the respective points. It is, however, realized that physical

meaning s of the variables in the equations are much different

from those in the Orr-Sommerfeld equation. In the same

paper, Tsugª=? has proved that the fluid moments obtained

from the one-particle kinetic equation are equivalent with the

Navier-Stokes equation(Nakagawa [9]), and the two-particle

version, the equations governing two-point correlations,

reduces to the KÂrman-Howarth equation.

The main purpose of the present paper is to obtain an exact

solution for the flow through a grid in the wind tunnel based

on the statistical theory of turbulence by Tsugª=?.

2. Equations Governing Boltzmann

Function F and Double Correlation

Function G

In order for Boltzmann function f and double correlation

function g to be identified by using variables in the BBGKY-

hierarchy theory, after Bogoliubov, Born, Green, Kirkwood

and Yvon, the following condition is required, for the

averaging time Ǽ must be longer than the time Ǽg for

satisfying the ergodicity;

Ǽ Ҝ Ǽg (1)

With the assumption (1), the dependent variables (f,g) may

be described by the general framework of the hierarchy

equations(Grad [10]):

У/ Уt+uкУ/Уy)e=J(aфÂ)[e Ô+g(a, Â)], (2)

(У/Уt +uкУ/Уy + ĬкУ/УˠICÂ

,Cф£=GI£Â«ICÂ?,Âф£= Ôg( «, e)+«IÔG?



where tertiary molecular chaos,

h(e, Ô, «)҂қَeَÔَ«Ҝ=0, (4)

has been adopted to truncate the hierarchy system. It may be

worth noting here that if one put g(a, Â)=қَeَÔҜ=0, binary

Open Journal of Applied Sciences

Supplement：2012 world Congress on Engineering and Technology

18 Cop

molecular chaos, the above hierarchy system reduces to the

Boltzman equation:

У/ Уt+uкУ/Уy)e=J(aфÂ)[e Ô].

3. Flow Through a Grid in Wind Tunnel

It may be evident that in the flow through a grid fixed

normal to the main flow direction , turbulence is generated and

then it decays with increasing the distance from the grid, by

experiencing the diffusion as well as viscous dissipation

mainly. This turbulence is the topic to obtain the exact

analytical solution.

The grid-produced turbulence is neither homogeneous nor

isotropic, but an isotropic, for there exists a specific vector of

the main flow direction(Fig.1).

Fig.1 Cross section of two-dimensional plane waves in

(x2,x3)-plane. x1: primary flow direction.

Let us assume the two-point correlation is separable in the

form,

RǩǪ(y,ˠ,t)=ě[ьo ǩ(y,t:ȁ)ǀě(ˠ,t:ȁ)dȁ], (5)

with

ǀ=o*(*;conjugate complex), (6)

where ȁis the constant separating the variables, ě[ ]denotes

taking real part.

Then, equations governing o ǩ reduces to a set of integro-

differential equations in the separated 3-dimensional space as

Уor/Уyr=0, (7)

(-iȁ+У/Уt+urкУ/Уyr -ǵкУ2/Уyr2)oj+Уuj /Уyrкor+1/

ǹкУo4/Уyj+У/Уyrьп-пor(Q)oj(ǡ-Q)dQ=0, (j,r=1,2,3).

(8)

 These (7) and (8) have been solved for the grid-produced

turbulence in the wind tunnel flow u=(U,0,0) with initial

fluctuations given at the plane;x1=0.

Instead of solving the complete boundary value problem, the

first analytical solution associated with the present theory is

sought to explain the existing experimental finding, viz., ̌the

inverse-linear decay law̍ of the turbulent intensity.

A. Formulation of the Problem

Let the grid-produced turbulence be composed of a plane

non-dispersive wave in the form,

oǩ=Qǩ(x1,ǡ)expާiǡ(Ǫ2x2+Ǫ3x3)ި,(ǩ=1,2,3,4)

(9)

with

Ǫ2=kкcosǰ, Ǫ3=kкsinǰ,

where ǰ is the azimuth angle of the oblique wave plane

normal to the mean flow direction(Fig.2).

Fig.2 Definition sketch of angles ǰandǾ

Let, then, Qǩmake a Fourier transform into Fǩ in order to

eliminate the nonlinear convolution integral of (8),

Qǩ(x1,ǡ)=1/(2Ǹ) ьп-пFǩ(x1,s)exp(-iǡs))ds. (10)

Note inverse Fourier transform Fǩ(x1,s) is defined as

Fǩ(x1,s)= ьп-пQǩ(x1,ǡ)exp(isǡ))dǡ,

where Qǩ(x1,ǡ) is an infinitely differentiable function of

bounded support.

Substituting (9), together with (10) into (7) and (8), we have

УF1/Уx1+ кУF2/Уs+Ǫ3кУF3/Уs=0, (11)

L(F1 ) + 1 /ǹкУF4/Уx1+NL(F1)=0, (12)

L(F2 ) + 1 /ǹкǪ2УF4/Уs+NL(F2)=0, (13)

Cop

L(F3 ) + 1 /ǹкǪ3УF4/Уs+NL(F3)=0, (14)

with

L=UУ/Уx1 - ǵЧ, (15)

Ч=У2/Уx12+(Ǫ22+Ǫ32)к У2/Уs2, (16)

NL= F1кУ/Уx1+( Ǫ2F2+Ǫ3F3)к У/Уs. (17)

Then, the following non-dimensional expressions are

introduced into (11)-14),

Ƕ= x1/M, ǯ=s/M, f1= F1/U, f2= F2/U, f3= F3/U, f4= F4/(ǹ

U2), Re=UM/ǵ, (18)

we obtain

Уf1/УǶ+Уf/Уǯ=0, (19)

Ȏ(f1)+ Уf4/УǶ+Ȣ(f1)=0, (20)

Ȏ(f)+ Уf4/Уǯ+Ȣ(f)=0, (21)

J(g)+H(g)=0, (22)

f=Ǫ2f2+Ǫ3f3, (23)

g=Ǫ3f2-Ǫ2f3, (24)

or, inversely

f2=( fкcosǰ+gкsinǰ)/k, (25)

f3=( fкsi nǰ-gкcosǰ)/k, (26)

J=У/УǶ-1/R eкЧ, (27)

Ч=У2/УǶ2+k2к У2/Уǯ2, (28)

H= f1кУ/УǶ+fкУ/Уǯ. (29)

The turbulent correlations defined by (5) may be also

expressed in terms of the Fourier transformed dependent

variables as follows,

RǩǪ(y,ˠ,t)=

U2/(2Ǹ)2ь02Ǹާь-ппfjfi d ǯިdǰ,(j,I;1,2,3). (30)

It may be justified that the grid-produced turbulence is axis-

symmetric with respect to the mean flow direction, namely,

homogeneous in any plane normal to its direction. Such a

turbulent flow is, therefore, described by superimposing the

plane waves considered here, and by averaging over the angle

ǰ within (x2,x3);

RǩǪ(y,ˠ,t)=U2/(2Ǹ)2ь02Ǹ

ީь-ппfj(Ƕ,ǯ)fiާǶ

, ǯ+krкcos(ǰ-Ǿ)ިdǯުdǰ,

with

r=ާ(x

^ 2-x2)2+(x

3-x3)2ި1/2,

where ǰ and Ǿ are angles defined in Fig.2

B. The Exact Solution of Grid-produced Turbulence

It may be straight forward that (19)-(22) are two-

dimensional, so that it may be possible to introduce a stream

function Ǡ in the form,

f1=УǠ/Уǯ, f=-УǠ/УǶ.

Then, combining (20), and (21) in order to eliminate f4, we

have

(J+ǠǯкУ/УǶ-ǠǶкУ/Уǯ)ЧǠ=0. (31)

This suggests that any harmonic function for Ǡ, namely,

solution of the Laplace differential equation, ЧǠ=0, turns out

to be an exact solution of the above full-nonlinear equation

(31). A particular solution, which is no more than a version

of the general solutions, the relevant integral constants being

specified by the boundary conditions at ǯ=дп, and Ƕ=п,

and whose components(ǠǶ, Ǡǯ) exhibiting the decay law,

may be expressed by

Ǡ=ǁarctan(ǯ/kǶ). (32)

It is easy to verify that by substituting (32) into the Laplace

differential equation

Ǡ=(У2/УǶ2+k2к У2/Уǯ2)Ǡ=0,

Ǡ is the solution. Moreover, substitution of (32) into (31)

results in the following relations,

f1=Ǡǯ=ǁ/( kǶ)ާ1+(ǯ/ kǶ)2ި-1, (33)

and

f=-ǠǶ= ǁǯ/( kǶ2)ާ1+(ǯ/ kǶ)2ި-1. (34)

The turbulent intensity in the Ƕ-direction, which is the non-

dimensional longitudinal coordinate of x1/M, can be

calculated by substituting f1 in (33) into (30), and integrating

it with respect to ǯ and ǰ, and results in

қ(Чu1)2 Ҝ/U2=ǁ2/(4kǶ), (35),

U2/қ(Чu1)2 Ҝ=4 kǶ/ǁ2. (36)

20 Cop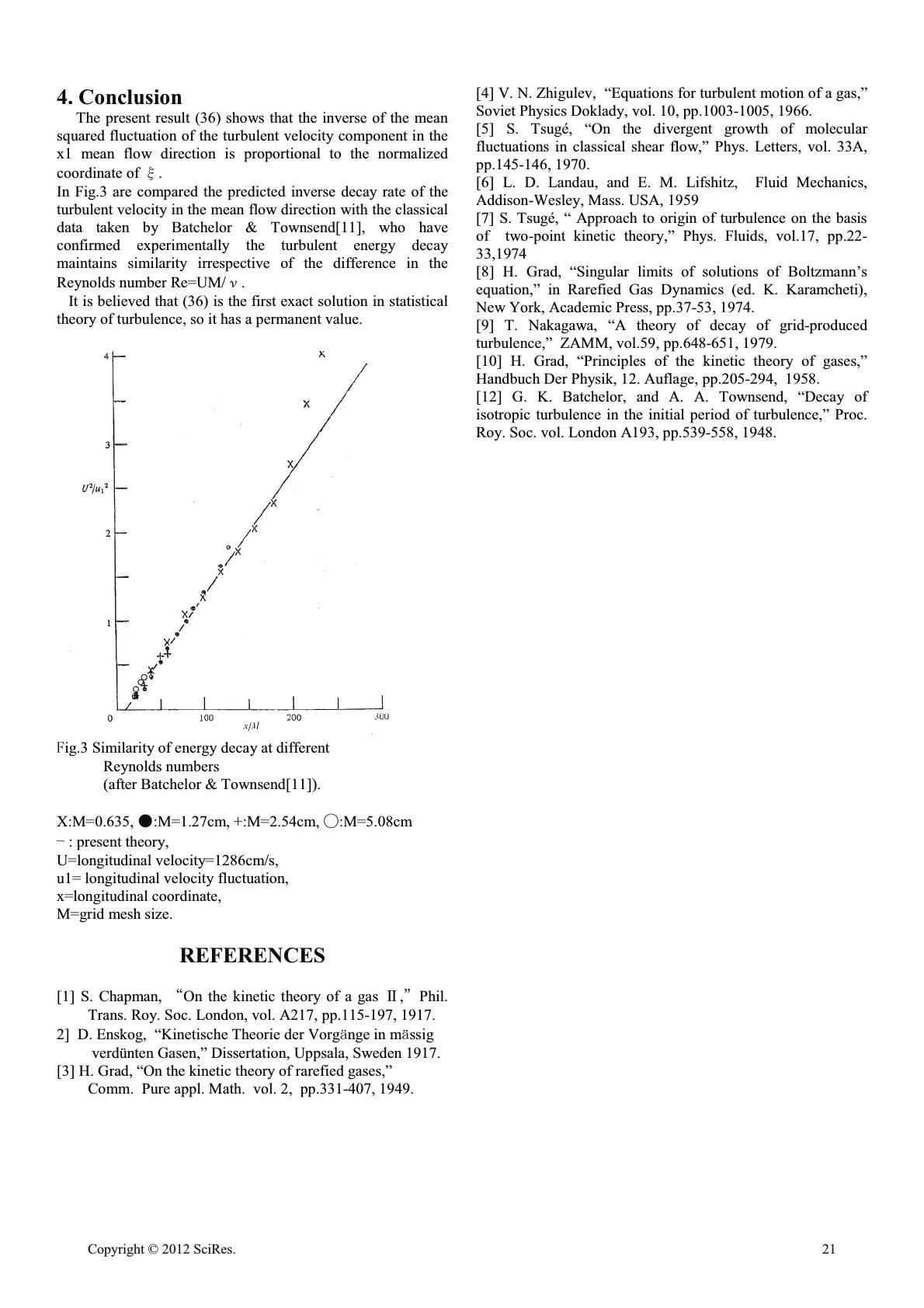

4. Conclusion

The present result (36) shows that the inverse of the mean

squared fluctuation of the turbulent velocity component in the

x1 mean flow direction is proportional to the normalized

coordinate of Ƕ.

In Fig.3 are compared the predicted inverse decay rate of the

turbulent velocity in the mean flow direction with the classical

data taken by Batchelor & Townsend[11], who have

confirmed experimentally the turbulent energy decay

maintains similarity irrespective of the difference in the

Reynolds number Re=UM/ǵ.

It is believed that (36) is the first exact solution in statistical

theory of turbulence, so it has a permanent value.

(ig.3 Similarity of energy decay at different

Reynolds numbers

(after Batchelor & Townsend[11]).

X:M=0.635, ٨:M=1.27cm, +:M=2.54cm, ڈ:M=5.08cm

г : present theory,

U=longitudinal velocity=1286cm/s,

u1= longitudinal velocity fluctuation,

x=longitudinal coordinate,

M=grid mesh size.



REFERENCES

[1] S. Chapman, ̌On the kinetic theory of a gas Τ,̍Phil.

Trans. Roy. Soc. London, vol. A217, pp.115-197, 1917.

2] D. Enskog, “Kinetische Theorie der Vorgˆnge in mˆssig

verdünten Gasen,” Dissertation, Uppsala, Sweden 1917.

[3] H. Grad, “On the kinetic theory of rarefied gases,”

Comm. Pure appl. Math. vol. 2, pp.331-407, 1949.

[4] V. N. Zhigulev, “Equations for turbulent motion of a gas,”

Soviet Physics Doklady, vol. 10, pp.1003-1005, 1966.

[5] S. Tsugé, “On the divergent growth of molecular

fluctuations in classical shear flow,” Phys. Letters, vol. 33A,

pp.145-146, 1970.

[6] L. D. Landau, and E. M. Lifshitz, Fluid Mechanics,

Addison-Wesley, Mass. USA, 1959

[7] S. Tsugé, “ Approach to origin of turbulence on the basis

of two-point kinetic theory,” Phys. Fluids, vol.17, pp.22-

33,1974

[8] H. Grad, “Singular limits of solutions of Boltzmann’s

equation,” in Rarefied Gas Dynamics (ed. K. Karamcheti),

New York, Academic Press, pp.37-53, 1974.

[9] T. Nakagawa, “A theory of decay of grid-produced

turbulence,” ZAMM, vol.59, pp.648-651, 1979.

[10] H. Grad, “Principles of the kinetic theory of gases,”

Handbuch Der Physik, 12. Auflage, pp.205-294, 1958.

[12] G. K. Batchelor, and A. A. Townsend, “Decay of

isotropic turbulence in the initial period of turbulence,” Proc.

Roy. Soc. vol. London A193, pp.539-558, 1948.







Cop