Paper Menu >>
Journal Menu >>
 Creative Education 2012. Vol.3, Supplement, 25-28 Published Online December 2012 in SciRes (http://www.SciRP.org/journal/ce) DOI:10.4236/ce.2012.37B006 Copyright © 2012 SciRes. 25 An Exploratory Study of Batch Splitting through Combined Control of Release and Dispatching Nuno O. Fernandes1, S. Carmo-Silva2 1School of Technology, Polytechnic Institute of Castelo Branco, Castelo Branco, Av. do Empresá rio 6000-767, Port ugal 2Dept. of Production and Syst ems, University of Minho, Braga, Campus de Gualtar 4710-057, Portugal Email: nogf@ipcb.pt, scarmo@dps.uminho.pt Received 2012 Workload Control (WLC) has been developed as a production planning and control approach for make-to-order manufacturing. Previous studies on WLC often assume a simplified shop where released batches are treated as independent jobs, which proceed through the different stages of processing without being split. Batch splitting allows released batches to be split into a number of smaller sub-batches so that its operations at work centres can be overlapped and its progress accelerated. This paper investigates how WLC performs under batch splitting. Evaluating the performance of WLC in this context is an important step towards the alignment between WLC theory and practice. Thus, assuming a production situation with unbalanced utilizations of manufacturing resources, the effectiveness of different dispatching rules and job release strategies are examined using simulation. Results highlight the importance of controlled re- lease of jobs to the shop floor and the importance of differentiating between bottleneck and non-bottleneck work centres for purpose of dispatching. Keywords: Order Release; Dispatchi ng; Batch Split t ing Introduction Workload Control (WLC) is a Production Planning and Con- trol (PPC) approach specifically designed for the needs of the make-to-order (MTO) industry and job shop manufacturing. It aims at firmly controlling job flow times through the produc- tion system by means of input/output control decisions towards meeting the promised delivery dates. Several WLC methods, varying in the degree of sophistica- tion, have been described in the literature [1]. A common de- nominator of these methods is the use of a pre-shop pool, where the jobs wait for a release decision, and a release mechanism [2]. The pre-shop pool can absorb fluctuations in the incoming flow of jobs, reduce disturbances caused by order cancellations, allow later ordering of raw materials and reduce the need to expedite jobs on the shop floor. The release mechanism make it possible to control the length of the queues on the shop floor, reduce shop congestion and increase load balancing among work centres, thus shortening and stabilising throughput times [3]. Past research in the field of WLC, essentially simulation based, often assumed that released batches (or jobs) proceed through the different stages of processing without being split ([4] and [5]). In contrast, this research investigates how WLC performs in shops where batch splitting is applied. Batch splitting allows released batches to be split into smaller sub-batches, which proceed independently, so that processing of its operations at work centres can overlap and its progress accelerated, as ob- served by [6]. Ref [7] also observed that batch splitting has great potential for helping improving due date performance. Ref [8] examined the impact of batch splitting in shops with varying flow dominance and concluded that flow shops are more likely to benefit from batch splitting than job shops. Later, [9] examined the performance of various release strategies in a DBR (Drum-Buffer-Rope) environment. They found that sig- nificant improvement in shop performance can be realized if batch splitting is allowed. The remainder of the paper is organized as follows. Section II briefly presents the focus of this research work. Section III outlines the simulation model and the experimental design be- fore the simulation results are presented and discussed in Sec- tion IV. Finally the concluding remarks and directions for fu- ture research work are put forward in Section V. Focus of This Res earch No research is available in the field of WLC that investigates how to take advantage of batch splitting for reducing delivery times, while maintaining high delivery reliability. In response, this research study investigates two release strategies, namely immediate release and the periodic with intermediate pull re- lease, and three dispatching strategies, assuming unbalanced resource (machine) utilizations levels and thus the existence protective capacity at non bottleneck resources. Experimenta- tions are conducted for a general flow shop, which is usually considered as having most in common with the real life job shops [10]. We seek a better understanding of the impact of release and dispatching strategies on the overlapping of operations and thus on throughput times. Splitting a release batch into a number of smaller sub-batches increases the probability of overlapping of operations and allows reducing throughput times. However, this is likely to require additional time being spent on setups, which  N. O. FERNANDES, S. CARMO-SILVA Copyright © 2012 SciRes. 26 may negatively affect performance, especially if these setups are on the bottleneck resources. Thus overlapping of operations and setup avoidance can be seen as competing objectives. While protective capacity and setup times can be studied across different levels, only one level is studied here because the purpose of this paper is to provide exploratory results. Simulation Study A simulation study has been set up using Arena® software to answer the research questions. During simulation experiments, data were collected under steady-state. The length of each rep- lication was 30000 time units with a warm-up period of 4000 time units. The average values of 100 independent replications are presented as the result of one experiment. Common random numbers were used as a variance reduction technique. Simulation Model We consider a six work centre general flow shop [12] with two bottlenecks and a single machine per work centre. The simulation model was kept simple to avoid interactions that might inhibit the full understanding of the effects being studied. As jobs arrive to the production system their due date, rout- ings and operation times are identified. It is assumed that all jobs are accepted and materials are available. As in previous studies [11] due dates are set using the TWK rule, Due Date = TNOW + c.TWK, where TNOW is the arrival time of the job, c is a constant and TWK is the total work content of the job. The value of c was set such that approximately 25% of the jobs were tardy under immediate released and first-come-first- served (FCFS) dispatching. This value was found to be suitable to show the relative behaviour of control strategies. Jobs inter-arrival times follow an exponential distribution, with the number of operations per job drawn from a discrete uniform distribution with a minimum of 1 and a maximum of 6. Six types of jobs are considered, each of which with an equal probability of being assigned to an arriving job. Released batches or jobs are split into smaller equal size sub-batches, which are then independently processed through the shop floor. The number of sub-batches in each release batch is drawn from a discrete uniform distribution with a minimum of 2 and a maximum of 4. Sub-batches are moved from one work centre to the next for processing without waiting for the entire job to be processed at the earlier work centre and thus allowing succes- sive operations of a job to be processed simultaneous. On the shop floor capacities of machines remain constant over time. Processing times were drawn from a truncated 2-Erlang distribution with a maximum that equals four times the mean value. The mean processing time at the bottleneck work centres was set to 1 time unit. The routings and process- ing times ensures that the average utilization at bottleneck work centre is 90% under FCFS dispatching and at the non-bottle- neck work centres is 80% of the utilization of the bottlenecks work centres. Each operation requires one specific work centre and return visits to same machine are not allowed. The setup-to-processing time ratio was set to 0.2 (20%). Setup times were assumed to be deterministic. Experimental Design and Parameters Settings The experimental factors and simulated levels considered in this study are summarised in Table 1. The release strategy was Table 1. Experimental factors and levels. Experimental factors Si mulated levels Job release strategy IMR PPR Dispatching strategy S1 S2 S3 Worload norm levels Inf inity, 14, 11 .9, 10.1, 8.6, 7.3, 6.2, 5.3, 4.5, 3.8 tested at two levels and dispatching was tested at three levels. These results in a full factorial design with 6, i.e. 2x3 combina- tions of settings. Combinations involving the controlled release of jobs have been run at 10 workload norm levels, in order to generate performance curves. The resulting total number of simulation experiments was 33. Two relea se strate gies we re invest igat ed in the study , namely : Immediate Release (IMR) and Periodic with intermediate Pull Release (PPR) [5]. In the former, jobs are released into the shop floor as they arrive, which means uncontrolled release of jobs to the shop floor. In the latter, jobs are considered for release accordingly to its urgency and released only if the resulting workload does not exceed predefined workload norms. A planned release date (PRD) is determined for each job in the pool, by subtracting the planned throughput time of each work centre in the routing of the job from the job’s due date. Jobs are then selected for release according to the PRD. At fixed periods of time the workload at work centres is computed and the deci- sion to release one or more jobs from the pre-shop pool is taken. Workload is accounted by the corrected aggregate load ap- proach. The corrected aggregate load has shown to be a robust and an effective approach, see [12]. Pull releases also may take place between periodic releases, every time the workload of any work centre falls to zero. In this case, only those jobs within the pre-shop pool that have the first operation at the starving work centres are considered for release. The selected job is not sub- jected to workload norms. Priority dispatching influences the pattern of batches pro- gress through its processing stages on the shop floor. Three dispatching strategies were considered in the study, namely: • S1: The earliest Planned operation Starting Time (PST) rule is applied to all work centres; • S2: The Setup Oriented Planned operation Starting Time (SOPST) rule is applied at the bottleneck work centres, whereas the PST rule is applied at the non-bottleneck work centres; • S3: The SOPST rule is applied to all work centres. Note that PST acts by giving priority to the jobs that become most urgent at each work centre. It is a commonly used rule within WLC (see e.g. [5]) and is focused on reducing the varia- tion of the lateness across jobs. The PST of a job j at work cen- tre v is determined as follows: jv jv jw wS PST dT ∈ = − ∑ (1) Where Tw is the planned throughput time at work centre w, Sjv is the set of work centres in the remaining routing of j after work centre v and dj is the due-date of job j. SOPST was recently introduced by [5]. It scans the queue for a job of the same type of that being processed. If no job is found, the job with the shortest PST is selected. Workload norms were tested at 10 levels of restriction in- cluding infinity, tightness steps were of 85%. In addition to 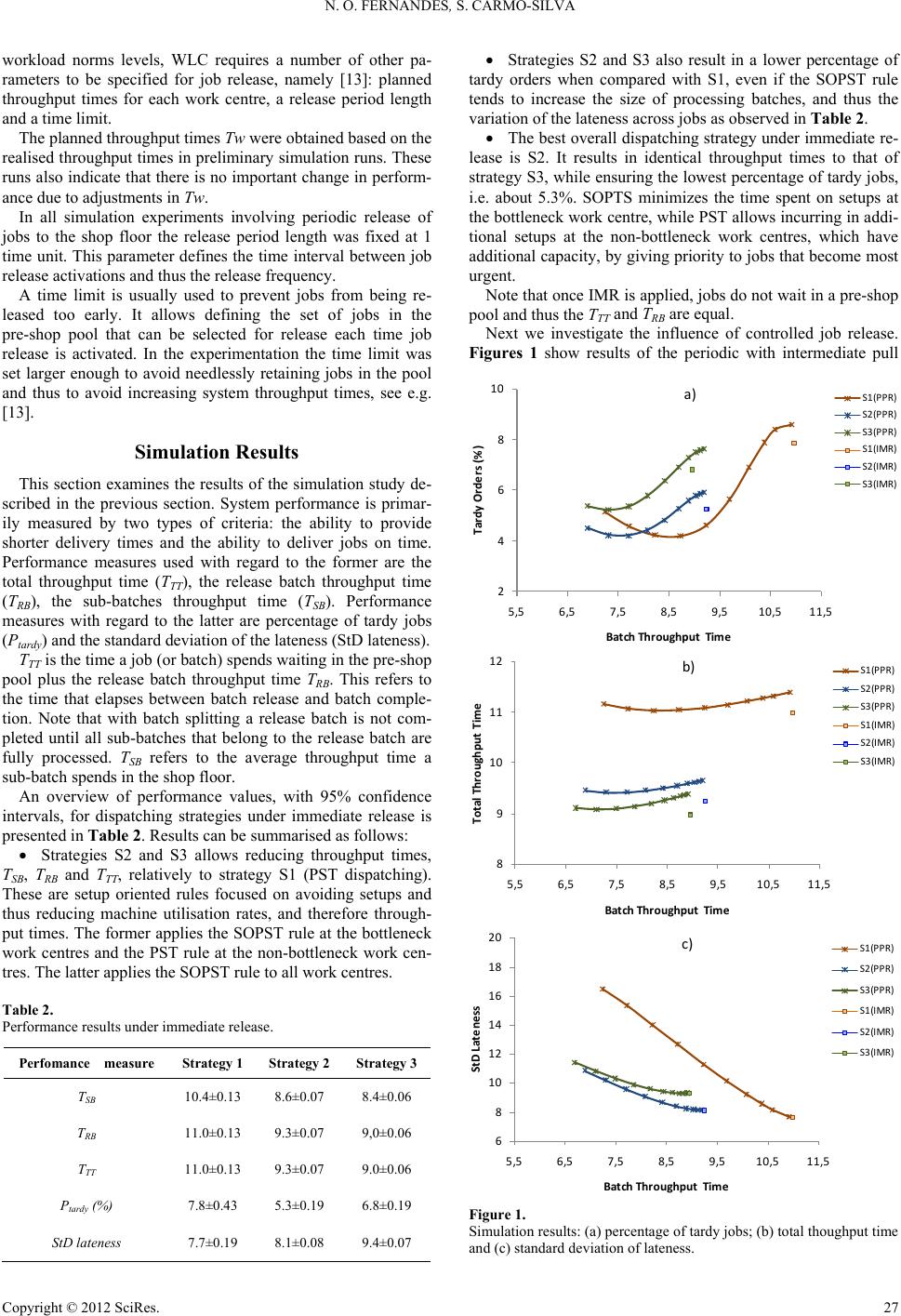 N. O. FERNANDES, S. CARMO-SILVA Copyright © 2012 SciRes. 27 workload norms levels, WLC requires a number of other pa- rameters to be specified for job release, namely [13]: planned throughput times for each work centre, a release period length and a time limit. The planned throughput times Tw were obtained based on the realised throughput times in preliminary simulation runs. These runs also indicate that there is no important change in perform- ance due to adjustments in Tw. In all simulation experiments involving periodic release of jobs to the shop floor the release period length was fixed at 1 time unit. This parameter defines the time interval between job release activations and thus the release frequency. A time limit is usually used to prevent jobs from being re- leased too early. It allows defining the set of jobs in the pre-shop pool that can be selected for release each time job release is activated. In the experimentation the time limit was set larger enough to avoid needlessly retaining jobs in the pool and thus to avoid increasing system throughput times, see e.g. [13]. Simulation Results This section examines the results of the simulation study de- scribed in the previous section. System performance is primar- ily measured by two types of criteria: the ability to provide shorter delivery times and the ability to deliver jobs on time. Performance measures used with regard to the former are the total throughput time (TTT), the release batch throughput time (TRB), the sub-batches throughput time (TSB). Performance measures with regard to the latter are percentage of tardy jobs (Ptardy) and the standard deviation of the lateness (StD lateness). TTT is the time a job (or batch) spends waiting in the pre-shop pool plus the release batch throughput time TRB. This refers to the time that elapses between batch release and batch comple- tion. Note that with batch splitting a release batch is not com- pleted until all sub-batches that belong to the release batch are fully processed. TSB refers to the average throughput time a sub-batch spends in the shop floor. An overview of performance values, with 95% confidence intervals, for dispatching strategies under immediate release is presented in Table 2. Results can be summarised as follows: • Strategies S2 and S3 allows reducing throughput times, TSB, TRB and TTT, relatively to strategy S1 (PST dispatching). These are setup oriented rules focused on avoiding setups and thus reducing machine utilisation rates, and therefore through- put times. The former applies the SOPST rule at the bottleneck work centres and the PST rule at the non-bottleneck work cen- tres. The latter applies the SOPST rule to all work centres. Table 2. Performance results under immediate release. Perfomance measure Strategy 1 Strategy 2 Strategy 3 TSB 10.4±0.13 8.6±0.07 8.4±0.06 TRB 11.0±0.13 9.3±0.07 9,0±0.06 TTT 11.0±0.13 9.3±0.07 9.0±0.06 Ptardy (%) 7.8±0.43 5.3±0.19 6.8±0.19 StD lateness 7.7±0.19 8.1±0.08 9.4±0.07 • Strategies S2 and S3 also result in a lower percentage of tardy orders when compared with S1, even if the SOPST rule tends to increase the size of processing batches, and thus the variation of the lateness across jobs as observed in Table 2. • The best overall dispatching strategy under immediate re- lease is S2. It results in identical throughput times to that of strategy S3, while ensuring the lowest percentage of tardy jobs, i.e. about 5.3%. SOPTS minimizes the time spent on setups at the bottleneck work centre, while PST allows incurring in addi- tional setups at the non-bottleneck work centres, which have additional capacity, by giving priority to jobs that become most urgent. Note that once IMR is applied, jobs do not wait in a pre-shop pool and thus the TTT and TRB are equal. Next we investigate the influence of controlled job release. Figures 1 show results of the periodic with intermediate pull 2 4 6 8 10 5,5 6,5 7,58,59,5 10,5 11,5 Tardy Orders (%) Batch Throughput Time a) S1(PPR) S2(PPR) S3(PPR) S1(IMR) S2(IMR) S3(IMR) 8 9 10 11 12 5,5 6,5 7,5 8,59,510,5 11,5 Total Throughput Time Batch Throughput Time b) S1(PPR) S2(PPR) S3(PPR) S1(IMR) S2(IMR) S3(IMR) 6 8 10 12 14 16 18 20 5,5 6,5 7,5 8,5 9,510,511,5 StD Lateness Batch Throughput Time c) S1(PPR) S2(PPR) S3(PPR) S1(IMR) S2(IMR) S3(IMR) Figure 1. Simulation results: (a) percentage of tard y jobs; (b) total thoughput time and (c) standard deviation of lateness.  N. O. FERNANDES, S. CARMO-SILVA Copyright © 2012 SciRes. 28 release (PPR) method. A logistic performance curve was de- veloped for each dispatching strategy, S1 to S3. Results are compared with IMR. The percentage of tardy jobs, total throughput time and the standard deviation of the lateness are plotted as a function of the average throughput time of release batches. A marker on a curve is the result of simulating the release method at a specific workload norm level. The right-hand mark on each curve refers to an experiment with infinite workload norms, i.e. meaning periodic unrestricted release. Tighter norms result in shorter release batch throughput times. Thus, the horizontal axis on each figure reflects the norm tightness level. Results can be summarised as fol l ow s: • From this curves it can be observed that controlling order release accordingly to the PPR method significantly reduces the percentage of tardy orders, relatively to IMR, even if it results in a high standard deviation of lateness, especially for tight workload norms. This essentially results from delaying orders in the pre-shop pool before release when workload norms are tightened. • The same as under IMR, dispatching strategy S2 results in the lowest percentage of tardy jobs when PPR is in place, particularly for tight workload norms. Likewise, strategy S1 also shows the worst performance for the percentage of tardy orders, but only for infinite or extremely loose workload norms. • The best control strategy, resulting in the lowest percent- age of tardy orders with the lowest batch throughput time, con- sists of combining PPR release with SOPST dispatching at the bottleneck work centre and PST dispatching at the non-bottleneck work centres, i.e. S2. Conclusions This paper presents the results of a simulation study of re- leasing and dispatching strategies in a general flow shop with unbalanced resource utilizations. Results highlight the importance of differentiating between bottleneck and non-bottleneck work centres for purpose of dis- patching. Dispatching strategies that tend to increase the size of processing batches (i.e. setup oriented) should be applied at the bottlenecks work centre, while dispatching strategies that sup- port the overlapping of successive operations of a job, and that may result in additional setups, should be applied at the non-bottleneck work centres. These work centres by definition have excess of capacity, which may be used to deal with the additional setups. Results also indicate that controlled release of order based on the periodic with intermediate pull release method performs better than immediate release for both the percentage of tardy orders and throughput times. Additional research is needed involving other shop configu- rations to increase understanding of the workload control con- cept in production systems with unbalanced resource utiliza- tions and batch splitting. In particular the exploration of bottle- necks at different routing positions shall be evaluated in future work. Acknowledgment This work had the financial support of FCT- Fundação para a Ciência e Tecnologia of Portugal under the project PEst-OE/ EME/UI0252/2011. REFERENCES Land, M. and Gaalman, G., “Workload control concepts in job shops: A critical assessment”, Int. Journal of Production Economics, Vol. 46–47, No.1, pp. 535-548, 1996. Hendry, L., Huang, Y. and Stevenson, M., “Workload control: Suc- cessful implementation taking a contingency-based view of produc- tion planning & control”, To appear in: Int. Journal of Operations and Production M anagement, 2012. Portioli A. and Tantardini, M., “A lean-based ORR system for non-repetitive manufacturing”. Int. Journal of Production Research, Vol. 50, No. 12, pp. 3257-3273, 2011. Fernandes, N.O. and Carmo-Silva, S., “Workload control under con- tinuous order release”, Int. Journal of Production Economics, Vol. 131, No. 1, pp. 257-262, 2011. Thurer, M., Stevenson, M., Silva, C, Land, M.J., and Fredendall, L.D., "Workload control (WLC) and order release: a lean solution for mak e-to-order companies" To appear in: Production and Operations Management, 2012. Jacobs, F.R. and Bragg, D.J., “Repetitive lots: flow time reductions through sequencing and dynamic batch sizing”, Decision Sciences, Vol.19, pp.281-294, 1988. Wanger, B.J. and Ragatz, G. L., “The impact of lot s plitting on due date performance”, Journal of Operations Management, Vol. 12, No. 1, pp.13-25, 1994. Smunt, T.L., Buss, A.H. and Kropp, D.H., “Lot Splitting in Stochastic Flow Shop and Job Shop E nvironments”, Decision Sc ience s , Vol. 27, No. 2, pp. 215–238, 1996. Russell, G.R., and Fry, T.D. (1997), “Order review/release and lot splitting in drum-buffer-rope”, Int. Journal of Production Research, Vol. 35, No. 3, pp. 827-845. Enns, ST, “An integrated system for controlling shop loading and work flows”. Int. journal of production research, Vol 33, No 10, 2801-2820, 1995. Fredendall, L.D., Divesh, O., and Patterson, J.W., “Concerning the theory of workload control”. European Journal of Operational Re- search, 201, 99–111, 2010. Oosterman, B., Land, M. and Gaalman, G.,“The influence of shop characteristics on workload control”, Int. Journal of Production Economics, Vol. 68, No. 1, pp. 107–119, 2000. Land, M., “Para meters and sensitivity in work load co ntr o l”, Int. Jo urn al of Production Economics , V ol. 104, No. 2, pp. 625–638, 2006. |

