Advances in Ma terials Physics and Che mist ry, 2012, 2, 31-34
doi:10.4236/ampc.2012.24B009 Published Online December 2012 (htt p://www.SciRP.org/journal/ampc)
Pulsed Gas Jets for Formation of High-Intensity
Cluster Beams
N. G. Korobeishchikov, A. E. Zarvin, V. V. Kalyada, A. A. Schmakov
Department of Applied Physics, Novosibirsk National Research State University, Novosibirsk, Russia
Received 2012
ABSTRACT
The possibility of using of pulsed supersonic gas jets for the formation of high intensity cluster ion beams are discusses. The resul ts
of experimental investigations of pulsed gases expansion are generalized in terms of dimensionless similarity parameters. The results
of the experimental study of formation of an high-intensity cluster beam of argon are presented. The fundamental phenomenon in-
fluences on the main parameters of cluster beam (cluster size, i ntensity ect.) are consid er ed.
Keywords: Puls ed Superso nic Jet; St eady-Flow Region; Settling Time; Condensation of Gas; Cluster Beam
1. Introduction
Today t he beams o f ato mic or mol ecular ion s are in fact beco me
an integral part of many modern technologies [1]. All conventional
ion beam technologies are based on the individual collisions (or
a cascade of binary collisions) of incident ions with near-
surface ato ms. A completely different situation occur s during a
collision the energetic large clusters with the surface. In this
case, nearly simultaneous interaction of many particles of
cluster around the same number of atoms in a solid occurs. This
leads to deposition a high-energy density into a very small
volume of the target material, an d stro ng nonlinear effects: lateral
sputtering, dry etching, and shallow implantation. Recently it
was shown that the accelerated gas cluster ion beams have a
number of unique advantages that allow them to be considered
a promising basis for new technologies, including nanotech-
nologies [2,3].
It’s known that in supersonic jet due to free expansion the
gas temperature drops to cryogenic values the process of
condensation occur and clusters can form [4]. A cluster can
consist of a large number of identical or different particles and
be in a different state of matter [5]. Forces, holding molecules
in the cluster, could effect on the threshold energy of activation
and ionization of molecules in a clusters, and result to
broadening of energy levels. Large particle residence time
increases the probability and intensity of energy exchange in a
cluster that allows you to talk about “cluster catalysis” [6-7].
Since the course of condensation is determined by the num-
ber of particle collisions during expansion, you must increase
the gas flow rate from th e source, what requires a proportionate
growth in the pumping performance of funds. Pulsed gas-jet
sources allow you to succesfully solve this problem. The
main advantage of pulsed sources compare to continuous flow
devices is the high economic efficiency, explained by their
relatively smaller dimensions, less stringent requirements on
pumping systems, and lower consumption of high-cost mate-
rials. In addition, pulse sources easily compatible with powerful
pul se activatio n systems: laser, disch ar ge, etc.
2. Dynamics of Gas Pulsed Expansion
Pulse regime assumes that the gas source operates for a finite
time wi th a certain se quence (fre que ncy a nd pulse ra ti o). T herefore,
the most important issue when using pulse source is the
formation at required distance from the source the flow with
sufficient duration and specified parameters, which similar
steady-flow expansion.
Obviously the dynamics of free gas expansion is determined
by the ratio of the momentum of the expanding gas to that of
the background gas. Depending on stagnation pressure P0 and
residual (background) pressure Pb we may distinguish three
principal regimes of supersonic pulsed expansion [8]:
a) expansion into a region of very low background pressure
(expansion into vacuum),
b) expansion into a continuous medium (flooded space),
c) expansion into a region with reduced background gas
pressu re (int er medi ate case).
The regime (a) requires the maintenance of a low back-
ground pressure (Pb < 10-2 P a). Other limiting regime (c, P b > 1
Pa) applies only for expansion of a cho ck-wave-heat ed gas. Fo r
practical applications most important conditions correspond to
regime (b, 1 < Pb < 10-2 Pa). The relatively high background
pressure allows the nozzle to operate at a large flow rate and
form supersonic flow with developed relaxatio n processes. We
have experi mentally invest igated th e gasdynamic para meters of
pulsed expansion of different gases (He, Ar, N2) from sonic
nozzles with diameters d = 1 mm and d = 0.5 mm. The main
parameters o f pu lsed jet are sett ling ti me of pul sed jet and du ra-
tion of steady-flow region.
2.1. Settling Time of Pulsed J e t
The settling time o f a nonsteady jet is defined as the time interval
from the moment of opening of the source to the moment of
establishment of steady flow parameters at a given distance
from the n ozzle. Th e settlin g ti me of a free j et is determined by
motion of the front part of the nonsteady flow, which depends

N. G. KOROBE ISHCHIKOV ET AL.
32
on the interaction of the expanding gas with the background gas,
namely depends on the ratio of the momentum of the expanding
gas to that of the background gas displaced from the flow re-
gion. Under expansion into vacuum (regime a) the leading front
of expansion gas move with the limiting velocity Vmn of non-
steady flow:
() ()
11
mm
Va γγ =∗+ −
(1)
where a* is sound velocity in the critical cross section of the
nozzle. But settling time is determined by the maximum velocity
of steady flow Vms, which is depend on the total enthalpy h0 of
this gas:
() ()
2 11
ms
V ha
γγ = =∗+−
(2)
It was found that under expansion into a region with reduced
background pressure (regime c) the retarding action of the
background gas leads to that the leading front of expansion gas
and the front of steady-flow region are t he same. The boun dary
of a pulsed jet propagates with a velocity significantly smaller
than the limiting steady-state value Vms for a given gas [8] .
In ord er to generali ze the experimen tal data, we used dimen-
sionless parameters including characteristics of the expanding
gas and the background gas, which play the role of similarity
criteria [9]. Using this date, it’s possible to calculate the settling
time of pulsed jet for actual conditions.
2.2. Duration of Steady-Flow Region
At moment of switch off gas source, there arises a trailing
(secondary) rarefaction wave characterized by nonsteady flow.
Propagation of this secondary rarefaction wave downstream
from the nozzle determines the trailing front of the steady flow
region. Therefore, a question naturally arises as to what is the
time of existence (or duration) of the steady flow at a given
distance from a puls ed jet source.
It was established that the length (duration) of the steady
flow regio n i n a p ul sed jet at a fixed di stan ce fro m the so u rce i s
independent of the ratio of heat capacities of expanding gases
and is determined by the pulse duration at the nozzle exit and
the ratio of stagnation and background pressures. The time of
Figure 1. Generalized plot of settling time in dimensionless coordi-
nates.
existence of the steady state in a pulsed gas jet monotonically
decreases downstream from the nozzle and drops with increas-
ing background gas pressure due to the loss of particles in the
leading and trailing rarefaction waves; this length increases
with th e initial momentu m because th e backgroun d gas is more
intensively displaced from the flow region [8]. As a result, a
situation is possible where the flow at a finite distance from the
sour ce do es n ot attai n a s tead y st ate ev en d esp ite t he fact t hat at
the nozzle necessary condi tions are satisfied.
2.3. Formation of High Intensity C l ust er Beams
Using pulse source we carried out experimentally research on
the formation of intensive cluster ions beams from the super-
sonic jets of Ar.
3. Experimental
The research was performed using the LEMPUS experimental
setup of Novosibirsk State University [10]. The pulse valve
with diameter of sonic nozzle 1 mm and the duration of gas
pulse
∼ 1.3 ms was used. The stagnation pressure P0 varying
from 1 kPa b efore 10 3 kPa. Th e measure ments were performed
by means of a molecular beam mass-spectrometer method
[11-12].
4. Results and Discussion
To determine the optimal parameters for the formation of an
intense cluster beam measurements of the total intensity of the
neutral molecular flow were made by varying the stagnation
pressure P0 and the distance of the nozzle - skimmer xns. The
measurements were performed using a closed ionization
pressure sensor Granville-Philips located on the axis of the
molecular b eam. Sin ce the clus ters are compl etely destr oyed b y
collisions with the walls inside the sensor, the equilibrium
density of the gas in the sensor is proportional to the intensity
cluster mol ecular b eam.
In Figure 3 shows the values of pressure on axis of molecu-
lar flow Pa and background pressure in the ionizer section Pb,
measured simultaneously at a fixed pressure P0 = 5*105 Pa at
different nozzle-skimmer distances. Here and further the dis-
tance nozzle - skimmer is measured in caliber (diameter of the
nozzl e throat), x/d *. There is an arrow shows the position of the
boundary of the jet - d irect shock wave (M ach disk), cal culated
from the known empirical formula:
0.67 .
Mk
X PP= ∗
(3)
where Pk is background pressure in the expansion chamber.
Obviously, the background pressure in the ionizer chamber may
influence the correctness of the sensor readings of the intensity
of the molecular beam. Therefore, the true pressure in the mo-
lecular beam Pmb defined as differ ence between Pa and Pb.
When moving from the Mach disk to the nozzle increases
leakage of gas through the skimmer into ionizer chamber ac-
cording to the isentropic density distribution of gas in the jet (~
1/x2, on the figure the dotted line). As a result, the background
pressu re Pb increases proportionally. The pressure of the mole-
cular beam Pmb also dramatically increased in proportion to ~
1/x2 after leaving the Mach disk (x/d* < 330). However, the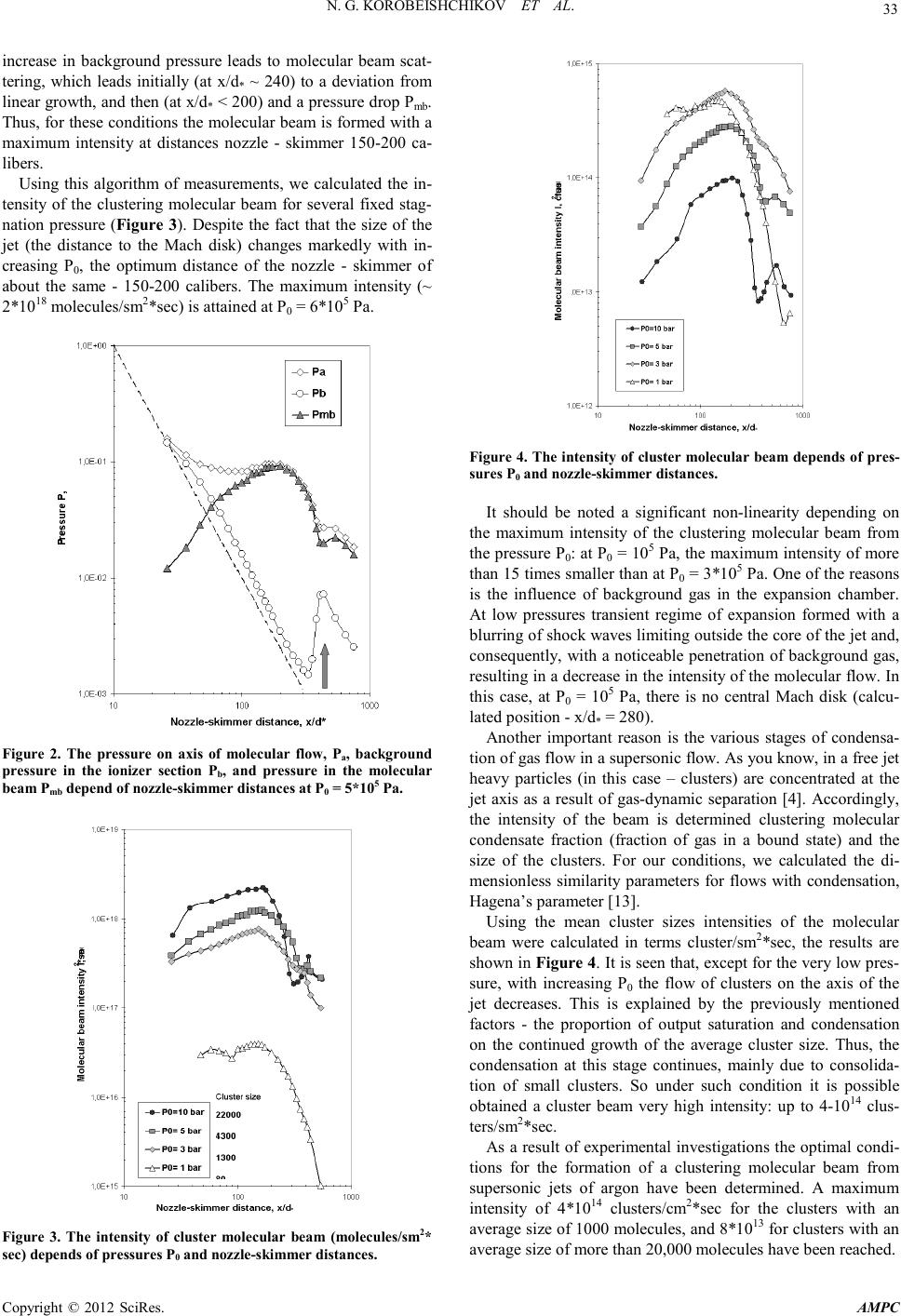

N. G. KOROBE ISHCHIKOV ET AL.
33
increase in background pressure leads to molecular beam scat-
tering, which leads initially (at x/d* ~ 240) to a deviation from
linear growth, and then (at x/d* < 200) and a pressure drop Pmb.
Thus, for these conditions the molecular beam is formed with a
maximum intensity at distances nozzle - skimmer 150-200 ca-
libers.
Using this algorithm of measurements, we cal culated the in-
tensity of the clustering molecular beam for several fixed stag-
nation pressure (Figure 3). Despite the fact that the size of the
jet (the distance to the Mach disk) changes markedly with in-
creasing P0, the optimum distance of the nozzle - skimmer of
about the same - 150-200 calibers. The maximum intensity (~
2*1018 molecules/ sm2*sec) is attained at P0 = 6*105 Pa.
Figure 2. The pressure on axis of molecular flow, Pa, background
pressure in the ionizer section Pb, and pressure in the molecular
beam Pmb depend of nozzle-skimmer d istances at P0 = 5*105 Pa.
Figure 3. The intensity of cluster molecular beam (molecules/sm2*
sec) depends of pressures P0 and nozzle-skimmer distances.
Figure 4. T he intensity of cluster molec ular beam depends o f pre s-
sures P0 and nozzle-skimmer distances.
It should be noted a significant non-linearity depending on
the maximum intensity of the clustering molecular beam from
the pressu re P0: a t P0 = 105 P a, t he max imu m in ten sit y of mo re
than 15 times smaller than at P0 = 3 *105 Pa. On e of the reason s
is the influence of background gas in the expansion chamber.
At low pressures transient regime of expansion formed with a
blurring of shock waves limiting outside the core of the jet and,
consequently, with a noticeable penetration of background gas,
resulting in a decrease in the intensity of the molecular flow. In
this case, at P0 = 105 Pa, there is no central Mach disk (calcu-
lated position - x/d* = 280).
Another important reason is the various stages of condensa-
tion of gas flow in a supersonic flow. As you know, in a free jet
heavy particles (in this case – clusters) are concentrated at the
jet axis as a result of gas-dynamic separation [4]. Accordingly,
the intensity of the beam is determined clustering molecular
condensate fraction (fraction of gas in a bound state) and the
size of the clusters. For our conditions, we calculated the di-
mensionless similarity parameters for flows with condensation,
Hagena’s parameter [13].
Using the mean cluster sizes intensities of the molecular
beam were calculated in terms cluster/sm2*sec, the results are
shown in Figure 4. It is seen that, except for t he very lo w pres-
sure, with increasing P0 the flow of clusters on the axis of the
jet decreases. This is explained by the previously mentioned
factors - the proportion of output saturation and condensation
on the continued growth of the average cluster size. Thus, the
condensation at this stage continues, mainly due to consolida-
tion of small clusters. So under such condition it is possible
obtained a cluster beam very high intensity: up to 4-1014 clus-
ters/sm2*sec.
As a result of experimental investigations the optimal condi-
tions for the formation of a clustering molecular beam from
supersonic jets of argon have been determined. A maximum
intensity of 4*1014 clusters/cm2*sec for the clusters with an
average size of 1000 molecules, and 8*1013 for clusters with an
average size of more than 20,000 molecules h ave been reached.

N. G. KOROBE ISHCHIKOV ET AL.
34
REFERENCES
[1] L.A. Giannuzzi and F.A. Stevens. Introduction to Focused Ion
Beams: Instrumentation, Theory, Techniques and Practice.
Springer Press. 2004.
[2] N.V. P o pok and E.B. Camp bell “B eams of atomic clus ters: ef fec t
on impact with solid,” Reviews of Advanced Materials Science,
vol. 11, pp. 19-45, 2006.
[3] I. Yamada, «Cluster ion beam process technology – 20 years of
R&D hist ory», Nuclear Instruments and Methods in Physics Re-
search B, vol. 257, pp.632-638. 2007.
[4] H. Pauly, Atom, Molecule, and Cluster Beams II. Sprin-
ger-Verlag, Berlin, 2000.
[5] Handbook of Nanophysics 2. Clusters and Fullerens. Ed. by
Klaus D. Scattler. New York: CRC Press, 2011.
[6] V. Zh. Madirbaev, A. E. Zarvin, N. G. Korobeishchikov and R.
G. Sharafutdinov, “Ion-cluster reactions initiated by an electron
beam in mixtures of argon with methane and monosilane,” Phys.
of the Solid Sta te, vol. 44, pp. 515-517, 2002.
[7] V. Zh. Madirbaev and A. E. Zarvin, “On the possibility of a
cluster-catalytic reactions for the synthesis of heavy hydrocar-
bons ,” Book of Abstr acts of th e 7th Int. Seminar on Flame Struc-
ture and First Young Res. Sch. on Flame Study. Novosibirsk,
July 11-15, p. 56, 2011.
[8] N. G. Korobeishchikov, A. E. Zarvin and V. Zh. Madirbaev,
“Hydrodynamics of pulsed supersonic underexpandet jets: Spati-
otemporal characteristic”, Tech. Phys., vol. 49, pp. 973-981,
2004.
[9] S. F. Chekmarev and N. V. Stankus, “Gasdynamic model and
similar relations for the starting process in supersonic nozzles
and jets”, Sov. Tech. Phys., vol. 29, pp. 920-925, 1984.
[10] A. E. Zarvin, N. G. Korobeishchikov, V. Zh. Madirbaev, G. G.
Gartvich, V. V. Kalyada and V. S. Airapetyan, “A universal
small-sized vacuum installation for gas-kinetic investigations”,
Instrum. Exp. Tech., vol. 43, pp. 641-649, 2000.
[11] N. G. Korobeishchikov, A. E. Zarvin, V. Zh. Madirbaev and R.
G. Shara futdinov, “Cond ensa tion of argon, monos ilane and their
mixt ur e in a puls e free j et” , Plas ma Chem . Pla sma P roc., vol. 2 5,
pp. 319-349, 2005
[12] A. E. Zarvin, N. G. Korobeishchikov, V. V. Kalyada and V. Zh.
Madirbaev, “Formation of mixed clusters in a pulsed he-
lium-oxygen-isoprene supersonic jet”, Eur. Phys. J. D, vol. 49,
pp. 101-110, 2008.
[13] O.F. Hagena, “Cluster ion sources,” Review of Science Instru-
ments, vol. 63, pp. 2374-2379, 1992.