Applied Mathematics, 2010, 1, 153-158
doi:10.4236/am.2010.13020 Published Online September 2010 (http://www.SciRP.org/journal/am)
Modified Efficient Families of Two and Three-Step
Predictor-Corrector Iterative Methods for Solving
Nonlinear Equations
Sanjeev Kumar1, Vinay Kanwar2, Sukhjit Singh3
1Department of Applied Sciences, ICL Institute of Engineering and Technology, Sountli, India
2University Institute of Engineering and Technology, Panjab University, Chandigarh, India
3Department of Mathematics, Sant Longowal Institute of Engineering and Technology,
Longowal, India
Received June 9, 2010; revised July 13, 2010; accepted July 16, 2010
Abstract
In this paper, we present and analyze modified families of predictor-corrector iterative methods for finding
simple zeros of univariate nonlinear equations, permitting


0fx


near the root. The main advantage of
our methods is that they perform better and moreover, have the same efficiency indices as that of existing
multipoint iterative methods. Furthermore, the convergence analysis of the new methods is discussed and
several examples are given to illustrate their efficiency.
Keywords: Nonlinear Equations, Iterative Methods, Multipoint Iterative Methods, Newton’s Method,
Traub-Ostrowski’s Method, Predictor-Corrector Methods, Order of Convergence
1. Introduction
One of the most important and challenging problems in
computational mathematics is to compute approximate
solutions of the nonlinear equation

0fx (1)
Therefore, the design of iterative methods for solving the
nonlinear equation is a very interesting and important
task in numerical analysis. Assume that Equation (1) has
a simple root r which is to be found and let 0
x
be our
initial guess to this root. To solve this equation, one can
use iterative methods such as Newton’s method [1,2] and
its variants namely, Halley’s method [1-6], Chebyshev’s
method [1-6], Chebyshev-Halley type methods [6] etc.
The requirement of

0fx
 is an essential condition
for the convergence of Newton’s method. The above-
mentioned variants of Newton’s method have also two
problems which restrict their practical applications rig-
orously. The first problem is that these methods require
the computation of second order derivative. The second
problem is that like Newton’s method, these methods
require the condition that


0fx
 in the vicinity of
the root.
For the first problem, Nedzhibov et al. [5] derived
many families of multipoint iterative methods by discre-
tizing the second order derivative involved in Cheby-
shev-Halley type methods [6]. We mention below only
one root-finding technique (2.1) from [5], namely






 
1
,
2
n
nn
n
nn
nn
nn n
fx
zxfx
fx fz
xz
f xfxfz 











, (2)
where


. For different specific values of

, vari-
ous multipoint iterative methods may result from (2).
For 1


in (2), we get


 
 
12
nnn
nn
nn n
fxfx fz
xx
f xfxfz

 

 



. (3)
This is the famous Traub-Ostrowski’s formula [1,2,4,5,
7,8], which is an order four formula. This method re-
quires one evaluation of the function and two evaluations
of its derivative per iteration. Thus the efficiency index
[2] of this method is equal to 34 1.587 which is bet-
ter than the one of Newton’s method 221.414. Fur-
thermore, Sharma and Guha [8] have developed a variant

S. KUMAR ET AL.
154
of Traub-Ostrowski’s method (3) which is defined by





 


 

 
1
,
,
2
,
2
n
nn
n
nn
nn
nn n
nnn
nn
nn n
fx
zxfx
fz fx
yzf xfxfz
fyfx afz
xy
fx fxafz








 








 
, (4)
where a is a parameter. This family requires an
additional evaluation of function

f
x at the point ite-
rated by Traub-Ostrowski’s method (3), consequently,
the local order of convergence is improved from four to
six. For 0a, we obtain the method developed by Grau
and Díaz-Barrero [7] defined by





 



 
1
,
,
2
,
2
n
nn
n
nn
nn
nn n
nn
nn
nn n
fx
zxfx
fz fx
yzf xfxfz
fy fx
xy
fx fxfz


 



 




  
. (5)
All these multipoint iterative methods are variants of
Newton’s method. Therefore, they require sufficiently
good initial approximation and fail miserably like New-
ton’s method if at any stage of computation, the deriva-
tive of the function is zero or very small in the vicinity of
the root.
Recently, Kanwar and Tomar [3,4] proposed an alter-
native to the failure situation of Newton’s method and its
various variants. They also derived modifications over
the different families of Nedzhibov et al. [5] multipoint
iterative methods. Unfortunately, the various families
introduced by Kanwar and Tomar [3] produces only
multipoint iterative methods of order three.
Recently, Mir et al. [9] have proposed a new predic-
tor-corrector method (designated as Simpson-Mamta
method (SM)), which is defined by

 

   
22
1
2,
4
6,
4/2
n
nn
nnn
n
nn
nnn n
fx
zx
fxpfxf x
fx
xx
fxfzxfz











 


. (6)
where p is chosen as a positive or negative sign so as to
make the denominator largest in magnitude. This method
is obtained by combining the quadratically convergent
method due to Mamta et al. [10] and cubically conver-
gent method due to Hasnov et al. [11]. This method will
not fail like existing methods if

f
x
 is very small or
even zero in the vicinity of the root. This method re-
quires one evaluation of the function and three evalua-
tions of its derivative per iteration. Thus the efficiency
index of this method is equal to 431.316 which is
not better than the one of Newton’s method 221.414
or Traub-Ostrowski’s method 34 1.587.
More recently, Gupta et al. [12] have developed a
family of ellipse methods given by

 
1222
n
nn
nn
fx
xx
f
xpfx
 , (7)
where 0p

 and in which

0fx
 is permitted
at some points in the vicinity of the root. The beauty of
this method is that it converges quadratically and more-
over, has the same error equation as Newton’s method.
Therefore, this method is an efficient alternative to
Newton’s method.
In this paper, we present two families of predictor-
corrector iterative methods based on quadratically con-
vergent ellipse method (7), Nedihzbov et al. family (2)
and the well-known Traub-Ostrowski’s Formula (3).
2. Development of Methods
2.1. Two-Step Iterative Method and its Order of
Convergence
Our aim is to develop a scheme that retains the order of
convergence of Nedzhibov et al. family (3) and which
can be used as an alternative to existing techniques or in
cases where existing techniques are not successful. Thus
we begin with the following predictor-corrector iterative
scheme


 

 

 
222
1222
,
,
2
n
nn
nn
nn
nn
nn
nn
fx
zx
fx pfx
fz fx
xz fx fz
fx pfx
















,
(8)
where the positive sign is taken if 0
x
r and the nega-
tive sign is taken if 0
x
r. Geometrically, if slope of
the curve




0
f
x  at the point



00
,
x
fx is nega-
tive, then take positive sign otherwise, negative. It is
interesting to note that by ignoring the term in p, pro-
posed family (8) reduces to Nedzhibov et al. family (2).
For 1


in (8), we get

S. KUMAR ET AL.
155

 
 
 
1222 2
nnn
nn
nn
nn
fxfx fz
xx
f
xfz
fx pfx




 



, (9)
This is the modification over the Formula (3) of Traub-
Ostrowski [2,5,7], and is also an order four formula. This
method requires same evaluation of the function and its
derivative as Traub-Ostrowski’s method per iteration.
Thus the efficiency index [2] of this method is equal to
34 1.587 which is better than the one of Newton’s
method22 1.414 or SM method 431.316. More
importantly, this method will not fail even if the deriva-
tive of the function is small or even zero in the vicinity
of the root.
The asymptotic order of this method is presented in
the following theorem.
Theorem 1. Suppose

f
x is sufficiently differen-
tiable function in the neighborhood of a simple root r and
that 0
x
is close to r, then the iteration scheme (8) has
3rd and 4th order convergence for
1) 1


,
2) 1


, respectively.
Proof: Since


f
x is sufficiently differentiable, ex-
panding


n
f
x and


n
f
x
 about
x
r by Taylor’s
expansion, we have
 


2345 6
2345nnnnnn n
fx frececececeOe




(10)
and
 


2345
234 5
12 345
nnnnnn
fxfrcecececeO e




(11)
where nn exr and


1, 2,3,...
!
k
k
fr
ck
kfr


Using Equations (10) and (11), we have


 
223345
232 4232
2374
n
nnnn n
n
fx ececcecccceOe
fx 
 (12)
Therefore,

 

 


222 2
2
22233 245
22322342
1
11
44814 63.
22
nn
nn n
n
n
nnnn n
fx fx
fx pfxfx
fxp fx
ececc pecccccpeOe







 
(13)
 

22233245
22322342
11
4410146 3.
22
nn nnn
fzf rceccp ecccccp eOe





(14)
   




22234
23 23
21244 .
nn nnnn
fxfzf r ececccpeOe 




(15)
Using Equations (12), (13) and (15), we obtain

 

 
222
2232
32224
242323
1644
22
8325 44.
n
nn
nn
nn
fz cecccp e
fx fz
ccccp ccpeOe



 


 

(16)
Using Equations (13)-(16) in Equation (8), we obtain,
 

2
2322 45
12232
217834914 4.
2
nn nn
p
ececcc eOe 

 

 
 
 

 (17)

S. KUMAR ET AL.
156
While for 1

 in (18), we have

3245
12 23
12.
2
nnn
ecccpeOe


 


(18)
Thus Equation (18) establishes the maximum order of
convergence equal to four, for iteration scheme (8). This
completes the proof of the theorem.
2.2. Three-Step Iterative Method and its Order
of Convergence
On similar lines, we also propose a modification over the
Formula (4) of Sharma and Guha [8]. Mir and Zaman [13]
have considered three-step quadrature based iterative
methods with sixth, seventh and eight order of conver-
gence for finding simple zeros of nonlinear equations.
Milovannović and Cvetković [14] further presented
modifications over three-step iterative methods consid-
ered by Mir and Zaman [13]. Also Rafiq et al. [15] have
presented similar three-step iterative method based on
Newton’s method with sixth-order convergence. All
these modifications are targeted at increasing the local
order of convergence with a view of increasing their ef-
ficiency index. But all these methods are variants of
Newton’s method and will not work if

f
x
 is very
small or zero in the vicinity of the root. To overcome this
problem, now we begin with the following predictor-
corrector iterative scheme

 

 

 

 
 
 
222
222
1222
,
,
2
,
n
nn
nn
nn
nn
nn
nn
nnn
nn
nn
nn
fx
zx
fx pfx
fz fx
yz fx fz
fx pfx
fyfx afz
xy fx bfz
fx pfx









 












(19)
where a and b are parameters to be determined from the
following convergence theorem.
Theorem 2. Let :
f
IR denote a real valued
function defined on I, where I is a neighborhood of sim-
ple root r of

.
f
x Assume that

f
x is sufficiently
differentiable function in I. Then the iteration scheme (19)
defines a one-parameter (.., )iea family of sixth order
convergence if 2ba and satisfies the following
error equation:




22 226
1223 23
7
122 412
4
.
n n
n
e cccpaccpe
Oe


(20)
Proof: follows on the similar steps as given in the pre-
vious theorem.
The proposed scheme (19) is now given by

 

 

 

 
 

 
222
222
1222
,
,
2
,
2
n
nn
nn
nn
nn
nn
nn
nnn
nn
nn
nn
fx
zx
fx pfx
fz fx
yz fx fz
fx pfx
fyfxafz
xy fx a fz
fx pfx









 












(21)
where a

. Note that for 0,p we obtain method (4)
obtained by Sharma and Guha [8] and for



,0,0pa ,
we obtain method (5) developed by Grau and Díaz-
Barrero [7].
3. Numerical Results
In this section, we shall present the numerical results
obtained by employing the iterative methods namely
Newton’s method (NM), Traub-Ostrowski’s method (3)
(TOM), Simpson-Mamta method (6) (SM), modified
Traub-Ostrowski’s method (9) (MTOM), method (4) for
1a

(3
M
) and modified method (21) for 1a

(3
M
M) respectively to solve nonlinear equations given
in Table 1. The results are summarized in Table 2. We
use 15 10

 as tolerance. Computations have been
performed using C

in double precision arithmetic.
Here all the formulas are tested for 1/2p. The fol-
lowing stopping criteria are used for computer programs:
1) 1nn xx


 ,
2)


1n
fx


.
The behaviors of existing multipoint iterative schemes
and proposed modifications can be compared by their
corresponding correction factors. The correction factor
()
,
()
n
n
f
x
f
x
 which appears in the existing multipoint itera-
tive schemes is now modified by
222
()
() ()
n
nn
f
x
f
xpfx

,
where 0p

. This is always well defined, even if
()0.
n
fx


It is investigated that formulas (8) and (21)
give very good approximation to the root when p is
taken in between 01p

. This is because that for
small value of p, the ellipse will shrink in the vertical
direction and extend along horizontal direction. This
means that our next approximation will move faster to-
wards the desired root. However, for 1p but not very
large, the formulas work if the initial guess is very close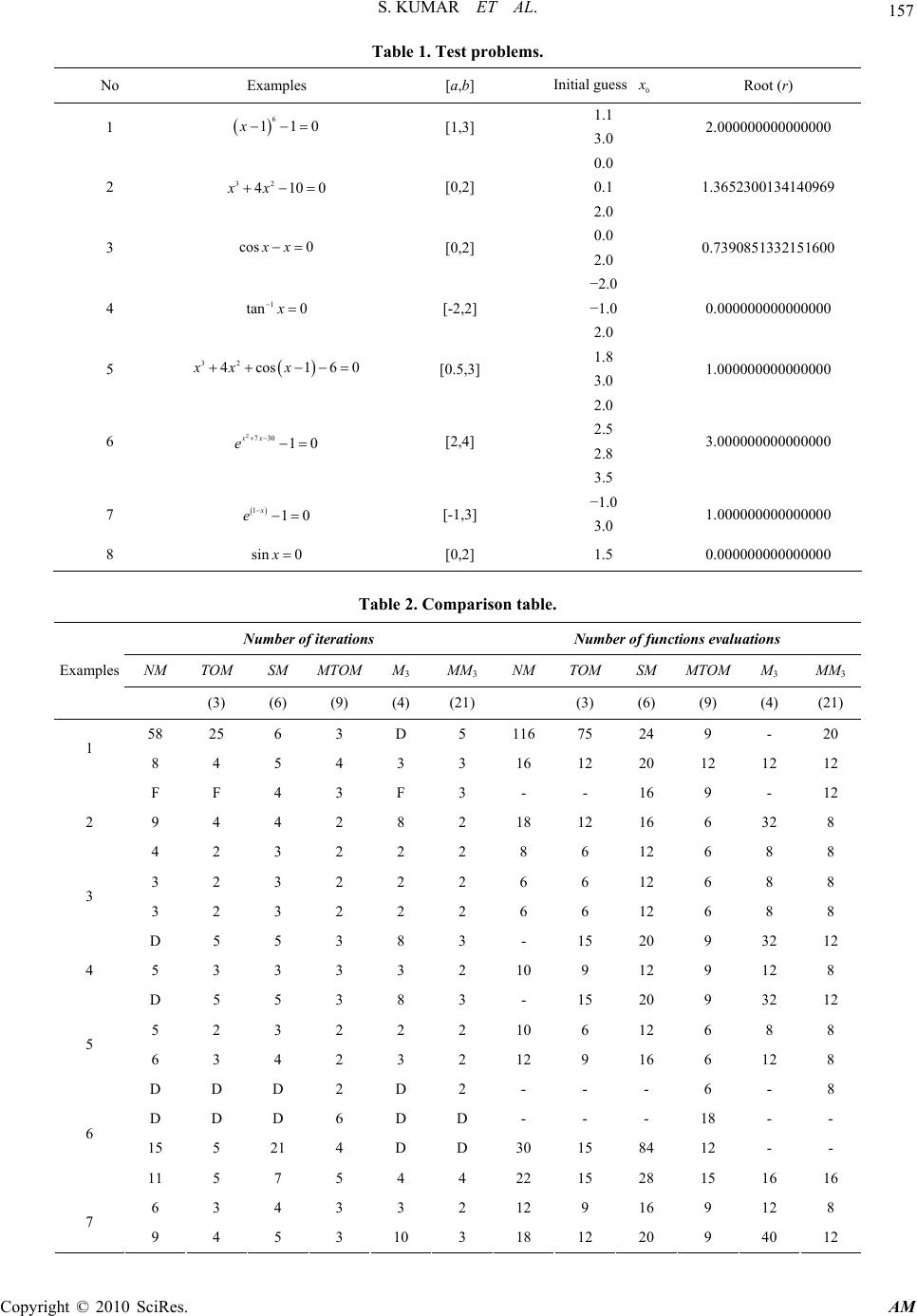

S. KUMAR ET AL.
157
Table 1. Test problems.
No Examples [a,b] Initial guess 0
x
Root (r)
1.1
1 
6
110x [1,3] 3.0 2.000000000000000
0.0
0.1 2 32 4100xx [0,2]
2.0
1.3652300134140969
0.0
3 cos 0xx [0,2] 2.0 0.7390851332151600
−2.0
−1.0
4 1
tan 0x
 [-2,2]
2.0
0.000000000000000
1.8
5 
32
4cos160xx x 
[0.5,3] 3.0 1.000000000000000
2.0
2.5
2.8
6 2730 10
xx
e  [2,4]
3.5
3.000000000000000
−1.0
7

110 x
e [-1,3] 3.0 1.000000000000000
8 sin 0x [0,2] 1.5 0.000000000000000
Table 2. Comparison table.
Number of iterations Number of functions evaluations
Examples NM TOM SM MTOMM3 MM3 NM TOM SM MTOM M3 MM3
(3) (6) (9) (4) (21) (3) (6) (9) (4) (21)
58 25 6 3 D 5 116 75 24 9 - 20
1
8 4 5 4 3 3 16 12 20 12 12 12
F F 4 3 F 3 - - 16 9 - 12
9 4 4 2 8 2 18 12 16 6 32 8 2
4 2 3 2 2 2 8 6 12 6 8 8
3 2 3 2 2 2 6 6 12 6 8 8
3
3 2 3 2 2 2 6 6 12 6 8 8
D 5 5 3 8 3 - 15 20 9 32 12
5 3 3 3 3 2 10 9 12 9 12 8 4
D 5 5 3 8 3 - 15 20 9 32 12
5 2 3 2 2 2 10 6 12 6 8 8
5
6 3 4 2 3 2 12 9 16 6 12 8
D D D 2 D 2 - - - 6 - 8
D D D 6 D D - - - 18 - -
15 5 21 4 D D 30 15 84 12 - -
6
11 5 7 5 4 4 22 15 28 15 16 16
6 3 4 3 3 2 12 9 16 9 12 8
7
9 4 5 3 10 3 18 12 20 9 40 12

S. KUMAR ET AL.
158
to the required root. For larger value of p, the formulas
do not work. This is perhaps due to the occurrence of
numerical instability in the process of computation.
Example 8. sin 0x.
This equation has an infinite number of roots. New-
ton’s method and Traub-Ostrowski’s method with initial
01.5x converge to 4

 far away from the required
root zero. Method (4) (3
M
) converges to 6

. Our
methods and SM method do not exhibit this type of be-
havior and converge to the nearest root zero.
4. Conclusions
The presented results indicate that the new proposed
methods are more efficient and perform better than clas-
sical existing methods. The computational results in Ta-
ble 2 show that the modified Traub-Ostrowski’s method
(MTOM) (9) requires a smaller number of function
evaluations than Newton’s method (NM) and Traub-
Ostrowski’s method (3) (TOM). The computational re-
sults in Table 2 also show that modified method (21)
(3
M
M) requires smaller number of function evaluations
than method (4) (3
M
). On similar lines, we can also
modify Mir and Zaman [13], Milovannović and Cvet-
ković [14] three-step iterative methods. Now a reasona-
bly close starting value 0
x
is not required for these
methods to converge. This condition, however applies to
practically all existing iterative methods for solving
equations. Moreover, they have same efficiency indices
as that of existing methods and do not fail if the deriva-
tive of the function is either zero or very small in the
vicinity of the root. Therefore, these techniques have a
definite practical utility.
5. Acknowledgements
We are grateful to the reviewer for the constructive re-
marks and suggestions which enhanced our work.
6. References
[1] A. M. Ostrowski, “Solution of Equations in Euclidean
and Banach Space,” 3rd Edition, Academic Press, New
York, 1973.
[2] J. F. Traub, “Iterative Methods for the Solution of Equa-
tions,” Prentice Hall, Englewood Cliffs, New Jersey,
1964.
[3] V. Kanwar and S. K. Tomar, “Modified Families of New-
ton, Halley and Chebyshev Methods,” Applied Mathe-
matics and Computation, Vol. 192, No. 1, September
2007, pp. 20-26.
[4] V. Kanwar and S. K. Tomar, “Exponentially Fitted Vari-
ants of Newton’s Method with Quadratic and Cubic Con-
vergence,” International Journal of Computer Mathe-
matics, Vol. 86, No. 9, September 2009, pp. 1603-1611.
[5] G. H. Nedzhibov, V. I. Hasanov and M. G. Petkov, “On
Some Families of Multi-Point Iterative Methods for
Solving Nonlinear Equations,” Numerical Algorithms,
Vol. 42, No. 2, June 2006, pp. 127-136.
[6] W. Werner, “Some Improvement of Classical Methods
for the Solution of in Nonlinear Equations in Numerical
Solution of Nonlinear Equations,” Lecture Notes Mathe-
matics, Vol. 878, 1981, pp. 426-440.
[7] M. Grau and J. L. Díaz-Barrero, “An Improvement to
Ostrowski Root-Finding Method,” Applied Mathematics
and Computation, Vol. 173, No. 1, February 2006, pp.
369-375, 450-456.
[8] J. R. Sharma and R. K. Guha, “A Family of Modified
Ostrowski Methods with July Accelerated Sixth Order
Convergence,” Applied Mathematics and Computation,
Vol. 190, No. 1, 2007, pp. 11-115.
[9] N. A. Mir, K. Ayub and A. Rafiq, “A Third-Order Con-
vergent Iterative Method for Solving Non-Linear Equa-
tions,” International Journal of Computer Mathematics,
Vol. 87, No. 4, March 2010, pp. 849-854.
[10] Mamta, V. Kanwar, V. K. Kukreja and S. Singh, “On a
Class of Quadratically Convergent Iteration Formulae,”
Applied Mathematics and Computation, Vol. 166, No. 3,
July 2005, pp. 633-637.
[11] V. I. Hasnov, I. G. Ivanov, and G. Nedzhibov, “A New
Modification of Newton’s Method,” Application of
Mathematics in Engineering, Heron, Sofia, Vol. 27, 2002,
pp. 278-286.
[12] K. C. Gupta, V. Kanwar and Sanjeev Kumar, “A Family
of Ellipse Methods for Solving Nonlinear Equations,” In-
ternational Journal of Mathematical Education in Sci-
ence and Technology, Vol. 40, No. 4, January 2009, pp.
571-575.
[13] N. A. Mir, K. Ayub and T. Zaman, “Some Quadrature
Based Three-Step Iterative Methods for Nonlinear Equa-
tions,” Applied Mathematics and Computation, Vol. 193,
No. 2, November 2007, pp. 366-373.
[14] G. V. Milovannović and A. S. Cvetković, “A Note on
Three-Step Iterative Methods for Nonlinear Equations,”
Studia University “Babes-Bolyai”, Mathematica, Vol. LII,
No. 3, 2007, pp. 137-146.
[15] A. Rafiq, S. Hussain, F. Ahmad, M. Awais and F. Zafar,
“An Efficient Three-Step Iterative Method with Sixth-
Order Convergence for Solving Nonlinear Equations,”
International Journal of Computer Mathematics, Vol. 84,
No. 3, March 2007, pp. 369-375.