Journal of Quantum Information Science, 2012, 2, 103-111
http://dx.doi.org/10.4236/jqis.2012.24016 Published Online December 2012 (http://www.SciRP.org/journal/jqis)
Quantum Teleportation with an Accelerated
Partner in Open System
Maohuai Xiang, Jiliang Jing*
Department of Physics, and Key Laboratory of Low Dimensional Quantum Structures
and Quantum Control of Ministry of Education, Hunan Normal University, Changsha, China
Received September 23, 2012; revised November 5, 2012; accepted November 14, 2012
ABSTRACT
We investigate the teleportation between two relatively accelerating partners undergoing the phase flip, bit flip and
bit-phase flip channels. We find that: 1) the fidelity decreases by increasing the acceleration of accelerated observer; 2)
the dynamic evolution of the fidelity is different for various channels if the acceleration is fixed; and 3) the fidelity is
always symmetric about 21
2


where

is a parameter of the transmission state.
Keywords: Quantum Teleportation; Non-Inertial Frames; Open System
1. Introduction
In recent years, quantum mechanics and quantum infor-
nmation science have developed rapidly. As one of the
significant characteristics of quantum mechanics [1], the
quantum entanglement has been attracted much attention
[2] and its momentous application is quantum teleporta-
tion proposed by Bennett et al. [3]. This application in-
volves many attractive theoretical features and shows a
bran-new way unlike classical teleportation [4-8]. How-
ever, the early study was confined to the inertial frame.
About ten years ago, P. M. Alsing et al. considered the
teleportation with an uniformly accelerated partner [9,10],
which firstly extended the quantum information to the
non-inertial frames. Since then, many authors focus on
this interdiscipline [11-16]. Moreover, some of them
studied the teleportation in some kinds of black hole
spacetimes and discussed how the Hawking effect affects
the entanglement and teleportation [17-21]. It is not
doubtful that these studies will makes the theories more
complete, not only for quantum information theory, but
also for relativistic quantum mechanics and quantum
field in curved spacetime.
It is well known that the interaction between quantum
system and surrounding environment is inevitably in our
real world, and then the dynamic evolution of the quan-
tum system is non-unitary (although the whole system
including the quantum system and surrounding environ-
ment evolves in an unitary fashion), so it becomes more
complex. Generally, this interaction can be viewed as the
interchange of information between quantum system and
surrounding environment. It plays a fundamental role in
the description of the quantum-to-classical transition
[22,23] and has been successfully applied in some im-
portant places such as the cavity QED [24] and ion trap
experiments [25]. So studying teleportation between two
relatively accelerated partners in open system is an inter-
esting topic, which not only makes the theory of the
quantum teleportation more complete, but also is helpful
for us to understand how the surrounding environment
affects the quantum teleportation. In this paper, we will
discuss teleportation for fermionic resources with one of
the EPR partners accelerated undergoing the environ-
ment, such as the bit flip, the phase flip, and the phase-bit
flip channels.
The outline of this paper is as follows. In Section 2 we
analyse the entangled state shared by two relatively ac-
celerated partners. In Section 3 we introduce the dy-
namics of the system interacting with the environment. In
Section 4 we investigate how the environment effects the
fidelity of the teleportation when teleportation undergoes
environment. And we summarize and discuss conclu-
sions in the last section.
2. Entangled State between Alice and Rob
We assume that an unknown state is teleported from Al-
ice who stays rest to Rob who moves with uniform ac-
celeration, and all our work is confined to Dirac field. As
shown in Refs. [26-29], the corresponding Unruh spinor
basis states can be described by a superposition of Unruh
*Corresponding author.
C
opyright © 2012 SciRes. JQIS

M. H. XIANG, J. L. JING 104
monochromatic modes
00,11
UU U




,
U

(1)
with
0cos0|0sin11
110,
II
UI I
UIII
rr




,
II

(2)
where the subscripts I and II represent Rindler regions I
and II,

speed of light in vacuum.
Considering Alice and Rob initially share the maxi-
mally entangled Bell state

100 11,
2AR AR
 (3)
then Alice stays stationary, while Rob moves with an
uniform acceleration. To describe the state shared by
them, we must rewrite the initial state (3). Using Equa-
tion (2), the state can also be represented as

12
2π
cos e1
ca
r




, is Rob’s acceleration, a

is the frequency of the Dirac particle, and is the c


2
2
1cos000 000cossin000 011
2
cos000110cossin011 000sin011 011
sin011110cos110 000sin110 011sin110110.
AR rrr
rrr r
rrr r
 


(4)
As we all known, the regions I and II of Rindler space-
time are causally disconnected, and our accelerated ob-
server must remain in either region I or II. Thus, for Rob
who stays in region I we must trace over the modes in
region II where he can’t access. After taking the trace,
Equation (4) in terms of matrix turns to be
2
2
cos00 cos
0sin 00 1.
20000
cos00 1
I
AR
rr
r
r










(5)
3. Environment
We discuss the local channel, in which each subsystem
interacts with its own environment and has no commu-
nication with others. Then the total evolution of state
s

can be expressed as [30]
11
() ,
N
sS
MMM M


 

 
N

(6)
where i
M

are the Kraus operators, N is the number of
the subsystems interacted with the environment. In clas-
sical computation, the bit flip is the only error
that will occur. However, there are the bit flip, the phase
flip and the phase-bit flip in quantum computation be-
cause of the possibility of the superposition. And the
Kraus operators for the three channels are given by [30]
01
01
121, 2
i
i
MpMp,

  (7)
where i = x gives us the bit flip, i = z the phase flip, and i
= y the phase-bit flip.
4. Teleportation in an Open System
Our teleportation model can be described as follow: Al-
ice and Rob share an entangled state at the beginning,
then Alice stays stationary, while Rob accelerates uni-
formly. Meanwhile, the whole system undergoes the
same environment, but each subsystem only interacts
with its own environment. And a client wants to send a
qubit state from Alice to Rob.
From above discussion we know that we can described
the evolved state of two particles undergoing local envi-
ronment as [31]

 
††
,
,
ARR A
ARijAR ij
ij
   
 (8)
where are the Kraus operators that de-
scribe the noise channels interacted with A and R. Now,
we will discuss the phase flip, bit flip and bit-phase flip
channels, respectively.


,
k
ikAR

4.1. Phase Flip Channel
The phase flip channel is a quantum noise process with
loss of quantum information but without loss of energy
[31-33]. For this channel, the Kraus operators are given
by [30-33]







0
()
1
0
1
diag12,121 ,
diag(2,2)1 ,
1diag12,1 2
1diag2,2,
A
AA
A
AAR
R
AR
R
ARR
pp
pp
pp
pp
 
 
 
 
,
R
R
where
 


0
AR AR
pp1

 is parameterized time in the
channel


A
R
pp
. For simplicity, we consider the special
situation that the decoherence rate is the same in both
channels, i.e. AR
p

.
Because Rob moves with an uniform acceleration, and
the whole system undergoes the phase flip channel, using
Equations (5) and (8), we obtain the evolved state

M. H. XIANG, J. L. JING 105

2
2
2
2
cos001 cos
10sin00
.
20000
(1)cos0 01
I
evo
AR
rp
r
pr






r










(9)
If we assume that the client wants to send the state
0
teleportation is: firstly Alice performs CNOT and Ha-
damard gate operation on the first two qubits, i.e.,
;
then she measures the two qubits in Z-basis. The total
state, after her measurement, will collapse to
 
††
1111 11
in
HCNOTCNOT H 
 
ij
I
ij ij

 with the probability of

1
4
I
ij AR
pTrij ij 



1

 
to Rob, considering the three subsys-
tems as a whole system, then the total initial state comes
to evo
in AR



. And the process of the quantum where ij
I

are given by
 
 

 
22
2
0
22 22
2
2
1
22 22
cos11 cos
1
=,
411cos sin
cos11 cos
1
=,
411cossin
i
i
Ii
i
i
Ii
rp
pr r
rp
pr r

 

 








 





 

2
r
r
(10)
finally Alice sends the results of the measurement (i and j)
to Rob by a classical information channel. According to
these information, Rob performs the corresponding
quantum gate

1
j
iij
X
ZZ

ijij ij
X on the qubit in his
possession, and getsi.e.,

†,
i j
II
ZX ZX  


22 2
2
0001
2 22
sin1 cos
1
,.
41coscos
ii
III
rp
pr r
 
 









r
(11)
Then, the fidelities


ij
ij I
FTr

 can be cal- culated analytically as


2
2242422 2
0
2
2242422 2
1
21coscos si
21coscos sin
i
i
n,
.
F
pr rr
F
pr r
 
 

r
(12)
From Equation (12), it is clear that the fidelities of the
teleportation depend on the channel parameter p, accel-
eration parameter r and state parameter

. In addition,
the suitable value of the fidelity should be the minimum
of the 0i
F
and 1i
F
since in reality Alice will not know
the result of the measurement as the quantum state.
Hereafter we take the minimum fidelity and plot them in
Figures 1 and 2.
Figure 1 shows that the fidelity decreases monoto-
nously as p increases, i.e., the transmission capacity con-
sistently weakened for this channel. Especially, when
21
2
  and , the fidelity
1p1
2
F, which means
that the fidelity will converge if the time of the interact-
tion between the system and environment is long enough,
and the information would never completely disappear.
However, when 1
3
  and 3
2
 , the fidelities
don’t gather even the environment interacts for infinite
time.
Figure 2 shows that the fidelity of the teleportation
has a symmetric point 212  . It is interest to note that
the fidelity is independent on when p20 

or
21


, which means that as the transmitted state is a
single bit the environment has no effect on the teleporta-
tion.
4.2. Bit Flip Channel
For the bit flip channel, the Kraus operators are



0diag12, 121
A
R
pp


 
121
AA
x
R
p 





01diag12,12
R
App
and
 
1112
R
R
A
px

 [30-33]. By using Equa-
tions (5) and (8), the initial state evolves to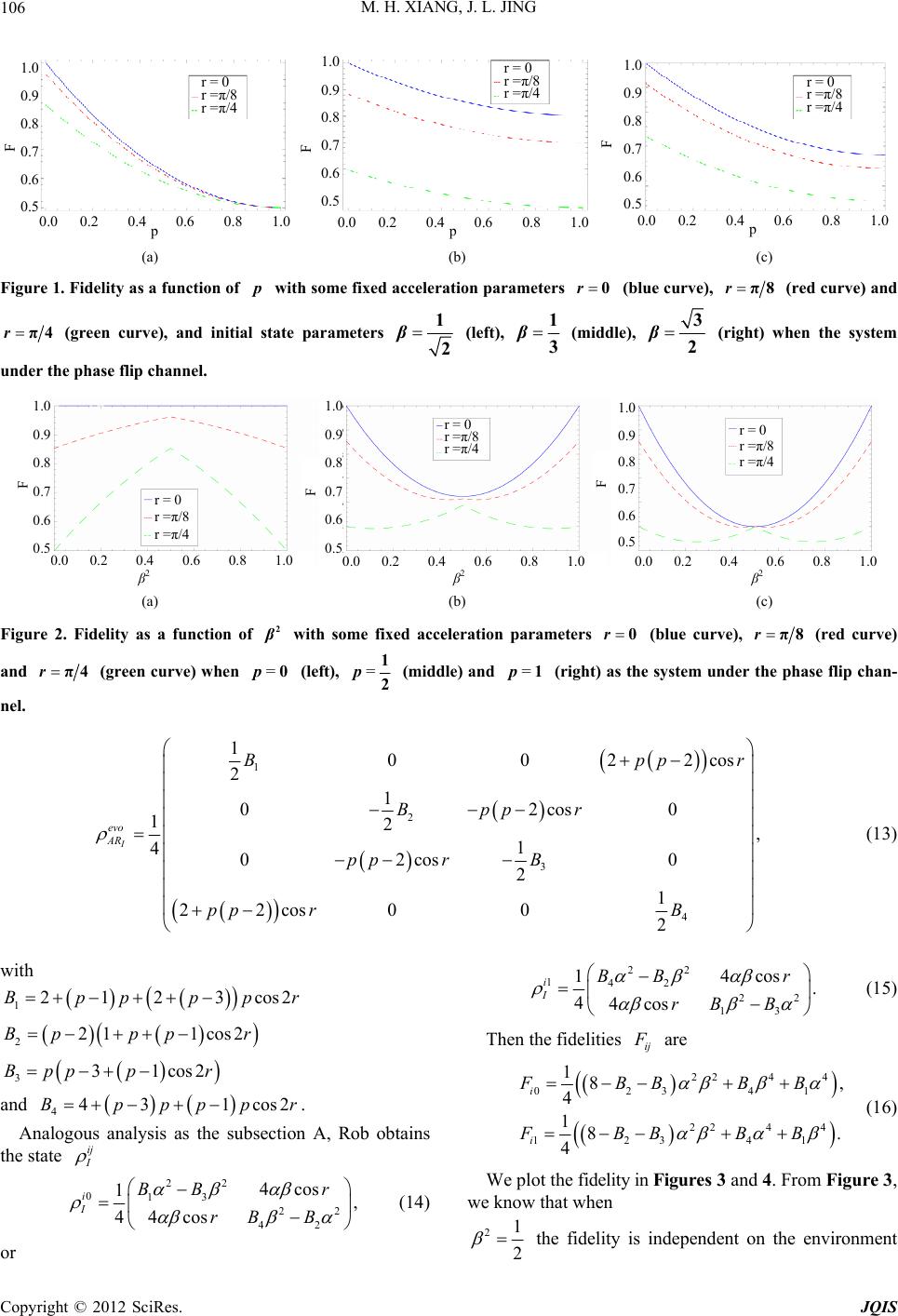

M. H. XIANG, J. L. JING 106
1.0
0.9
0.8
0.7
0.6
0.5
F
0.0 0.2 0.4 0.6 0.8 1.0
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4 r = 0 r =π/8
r =π/4
p
1.0
0.9
0.8
0.7
0.6
0.5
F
1.0
0.9
0.8
0.7
0.6
0.5
F
0.0 0.2 0.4 0.6 0.8 1.0
p
0.0 0.2 0.4 0.6 0.8 1.0
p
(a) (b) (c)
Figure 1. Fidelity as a function of with some fixed acceleration parameters p

0r (blue curve), π8r (red curve) and
π4r (green curve), and initial state parameters 1
2
β (left),

1
3
β (middle), 3
2
β (right) when the system
under the phase flip channel.
1.0
0.9
0.8
0.7
0.6
0.5
F
0.0 0.2 0.4 0.6 0.8 1.0
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
1.0
0.9
0.8
0.7
0.6
0.5
F
1.0
0.9
0.8
0.7
0.6
0.5
F
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0
β2 β2 β2
(a) (b) (c)
Figure 2. Fidelity as a function of 2
β
with some fixed acceleration parameters

0r (blue curve), π8r (red curve)
and π4r (green curve) when (left), =0p=1
2
p (middle) and (right) as the system under the phase flip chan-
nel.
=1p




 
1
2
3
4
10022
2
1
02cos
12,
1 402cos 0
2
1
22cos 002
I
evo
AR
Bp
Bppr
pp rB
pp rB










 





cos
0
pr
2 r
2r
(13)
with
  
12123cosBpppp  
 

221 1cos2Bp ppr 
 
331cos2Bpppr
and .

443 1cosBpppp  
Analogous analysis as the subsection A, Rob obtains
the state ij
I

22
013
22
42
4cos 1,
44cos
i
I
BB r
rB B
 
 







(14)
or
22
142
22
13
4cos
1.
44cos
i
I
BB r
rB B







(15)
Then the fidelities ij
F
are




224 4
02341
224 4
12341
18,
4
18.
4
i
i
FBBBB
FBBBB

 
 
 
(16)
We plot the fidelity in Figures 3 and 4. From Figure 3,
we know that when
21
2


the fidelity is independent on the environment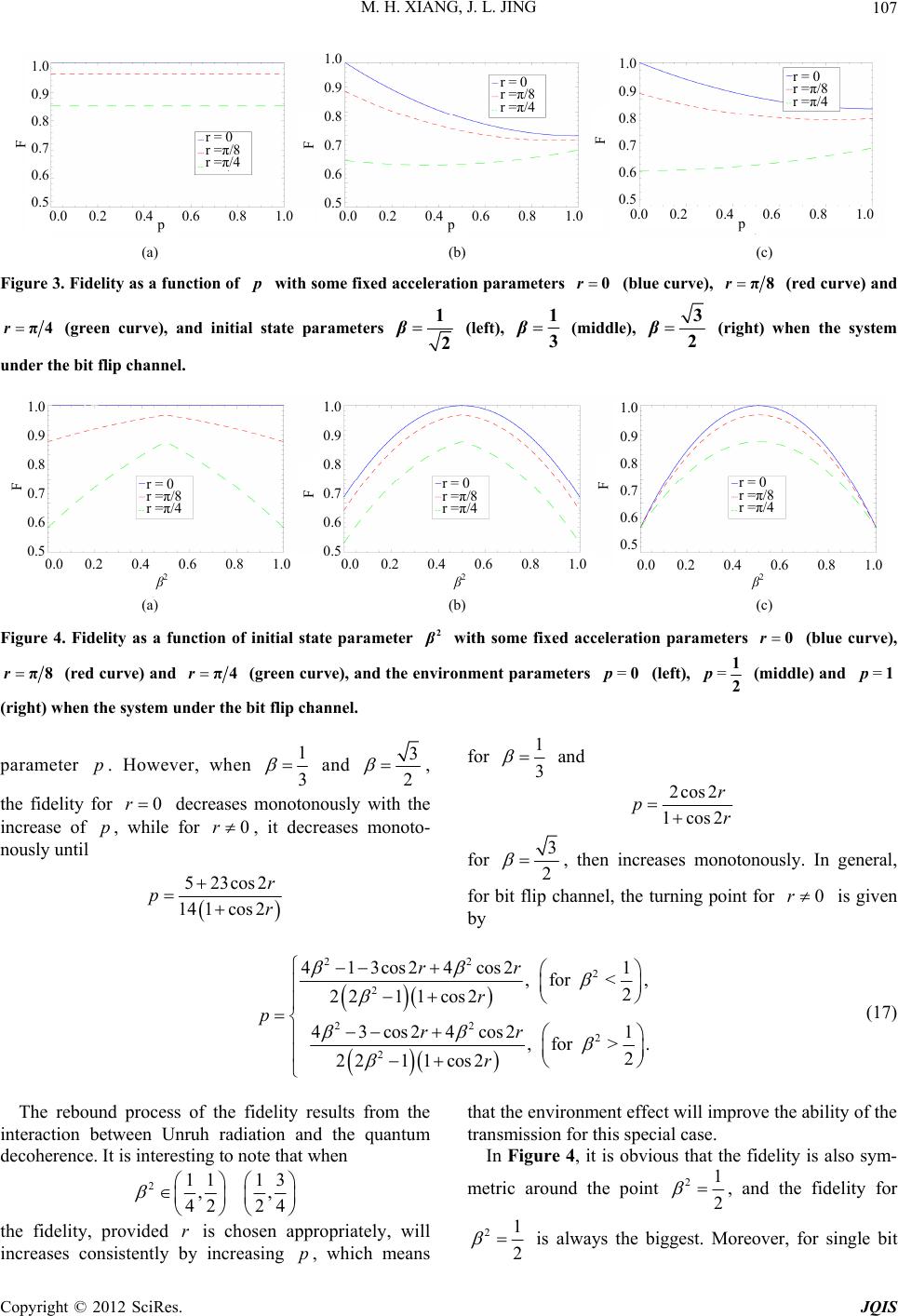

M. H. XIANG, J. L. JING 107
1.0 1.0
0.9
0.8
0.7
0.6
0.5
0.9
0.8
0.7
0.6
0.5
F
0.0 0.2 0.4 0.6 0.8 1.0
1.0
0.9
0.8
0.7
0.6
0.5
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
F
F
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.2 0.4 0.6 0.8 1.0
p pp
(a) (b) (c)
Figure 3. Fidelity as a function of with some fixed acceleration parameters

0r
p
(blue curve), π8r (red curve) an d
π4r (green curve), and initiatate parameters l s1
2
β (left),

1
3
β (middle), 3
2
β (rwhen the system
he bit flip channel.
ight)
under t
1.0
0.9
0.8
0.7
0.6
0.5
F
0.0 0.2 0.4 0.6 0.8 1.0
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
1.0
0.9
0.8
0.7
0.6
0.5
F
1.0
0.9
0.8
0.7
0.6
0.5
F
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0
β2 β2 β2
(a) (b) (c)
Figure 4. Fidelity as a function of initial state parameter 2
β
w ith some fixed acceleration parameters (blue curve), 0r
π8r (red curve) and π4r (green curve), and the enronment parameters =0p (left), vi =1
2
p (mie) and =1p
hen the system undit flip channel.
arameter p. However, when
ddl
(right) wer the b
p1   and 3
2
 
3,
fo onotowith ththe fidelity r 0r decreases mnously e
increase of , while for 0rp

, reases m- it deconoto
nously until

52 s2r
1
3


and
3co
141cos 2
pr 
for
2cos2
1cos2
r
pr 
for 3
2
 , then increases monoously. In general,
it flip c
ton
for bhannel, the turning point for 0r is given
by




22
2
2
22
2
2
413cos24cos2 1
, for <,
2
221 1cos2
43cos24cos21
, for >.
2
221 1cos2
rr
r
prr
r






 

 

 

 

(17)
The rebound process of the fidelity results from the
teraction between Unruh radiation and the quantum
e
in
dcoherence. It is interesting to note that when
21113
,,
42 24




the fidelity, provided is chosen appropriately, will
increases consistently by increasing , which means
that the environment effect will improve the ability of the
transmission for this special case.
In Figure 4, it is obvious that the fidelity is also sym-
metric around the point
r
p
21
2
 , and the fidelity for
21
2


is always the biggest. Moreov r, for single bit e

M. H. XIANG, J. L. JING 108

0or 1   the difference of the fidelities of dif-
ferent r cases will becomes smaller and smaller with
the increase of p. Especially, when 1p they con-
verge to 1 F.
2
4.3. Bit-Phase Flip Channel
For this channel, the Kraus operators are



0diag12, 12
A1
R
pp


 
121
AA
y
R
p 





01diag12,12
R
App
 
112
R
R
Ay
p

 and [30-33]. Using Equations (5)
and (8), the evolved state is given by
 




1
2
3
4
02
2
1
02cos0
12.
1 402cos 0
2
1
22cos2 002
I
evo
AR
Bpr
Bppr
pprB
pprB















(18)
After analogous analysis done in the Section 4.3, the
final state
1

022cosp
ij
I

Rob obtained is


222
42
,
441
cos
Ipr
BB   



(19)
2
22
13
041cos
1BBp r
 



or
i



2
22
42
1
222
13
41cos
1.
441cos
i
I
BBp r
prBB
 
 









(20)
The fidelities ij
F
are






12
1
=8 1
ip
BB


2224 4
02341
2224 4
341
181
4
.
4
i
FpBBBB
F BB
,




 
 
(21)
We plot the fidelity of the teleportation in Figures 5
and 6. We can see from Figure 5 that different fidelities
corresponding to different acceleration parameters r will
finally converge to the point with the value of

1
2
F

.
For 21
2


, the fidelity is monotonously decrease as
ment.
an
p increases. That is to say, the transmitting capacity
becomes weaken when the system interacts with the en-
vironHowever, provided 0r, the fidelity de-
creases at the beginning, then increases monotonously,
d the turning points are

35128cos161cos 2
24964cos49cos 2
rr
prr

 r fo1
3
  and


23cos cos2rr
p  for 3
2
rning point0
16 cos cos2 rr 
 , respectively. In
general, for bit-phase flip the tu for r

is






 




 
 
 

22222
2
2
2
sec 1
,f or <,
2
2 cos
r
r 



22
44 1 1 




22 2 22
2
2
22 2
161cos2 14 143cos2
161cos214341cos2sec1
,for >.
2
441 12cos
rr
p
rrr
r
 
 





 





(22)
It is worthy to point that the turning point could close
to but never reach it with any acceleration.
Figure 6 also shows that the fidelity is symmetric
ar
0p
ound the axis 21
2
 . And we are interested to note
that th
i.e
environment is long enough, both the initial state and
Rob’s acceleration doesn’t affect the fidelity any more, it
is always
e fidelity, when 1p, is invariant for any β and r,
., when the time of interaction between subsystem and
1
2
F

.
5. Summary
The quantum teleportaetween two relatively accel
tion b

M. H. XIANG, J. L. JING 109
1.0
0.9
0.8
0.7
0.6
0.5
F
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
1.0
0.8
0.7
0.6
0.5
0.9
1.0
0.9
0.8
0.7
0.6
0.5
F
F
0.0 0.2 0.4 0.6 0.8 1.0
p 0.0 0.2 0.4 0.6 0.8 1.0 p
p
0.0 0.2 0.4 0.6 0.8 1.0
(a) (b) (c)
Figure 5. Fidelity as a function of the environment parameterswith some fixed acceleration parameters p

0r (blue
curve), π8r (left), 1
3 (mi (green curve), anditial state parameters in 1 2
β (red curve) and π4rβddle),
3
2
β (right) when the system under the phase-bit flip channel.
1.0
0.8
0.9
0.7
0.6
0.5
F
0.0 0.2 0.4 0.6 0.8 1.0
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
r = 0
r =π/8
r =π/4
1.0
1.0
0.9
0.8
0.7
0.6
0.5
0.9
0.8
0.7
0.6
0.5
F F
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0
β2 β2 β2
(a) (b) (c)
Figure 6. Fidelity as a function of initial state parameter 2
β
with some fixed acceleration parameters (blue curve), 0r
π8r (green curve), and theronment parameters (left), envi=0p=1
2
p (middl(red curve) and π4r e) and
(right) when the sys
bit-phase flip channels is studied. It was shown that the
fidelityion de
it-
=1p
tem under the phase-bit flip channel.
erated partners undergoing the phase flip, bit flip, and
of the teleportatpends on the acceleration
parameter r, environment parameter p and transm
d state parameter te

. By fixing p and

, the fidel-
F e
ity is consistently decreases with the increase of the ac-
celeration. However, by fixing r, the dynamic evolution
of the fidelity has different properties, which are listed as
follows: 1) or the phase flip channel, th fidelity is mo-
notonously reduced as p increases. When 21
2


, the
fidelity will converge to 1
2
F after a long time of the
interaction between the system and the environment; 2)
For the bit flip channel, when 21  , the fidf the
teleportation is not affec the environment at all.
2elity o
ted by
But when 21
2
 , the fidelity will emerge a turning
point at the p axis. Before nt the fidelity de-
creases monotonously and after increases
the poi
that the fidelity
d be n
hosenriate can
increase monotonously with the increase of when
monotonously. However, the fidelity decreases all the
time if Rob is not accelerated. It shouloted out that,
provided r is c approply, the fidelity
p
21113
,,
42 24
 


; And 3) for the phase-bit channel,

ities coall the fidelnverge to one point 1 F for any
2
acceleration and any transmission state parameter

if
the time of the interaction between the system and the
environment is long enough. The fidelity is also mo-
notonouslydecreasing when 21
2
  or the acceleration
is zero in this channel.
In addition to that,
ronment the fidelity is always symmetric about
undergoing any of the three envi-
21
2


as it is a function of the transmission state parameter

.
And it, as 20 

or 21 

, is constant for the pse
flip channel, while it is constant with
ha
21
  for the bit
2

M. H. XIANG, J. L. JING 110
flip channel, which indicates that there are the different
characters between these environments.
nts
Th
75065
10935013; the National Basic Research of China
0003; PCSIRT,
n of C
ogram of t
NCES
6. Acknowledgeme
is work was supported by the National Natural Sci-
ence Foundation of China under Grant No. 111,
under
Grant No. 2010CB833004; the SRFDP under Grant No.
2011430611No. IRT0964; the Hunan
Provincial Natural Science Foundatiohina under
Grant No 11JJ7001; and Construct Prhe Na-
tional Key Discipline.
REFERE
[1] A. Einstein, B. Podolsky and N. Rosen, “Can Quantum-
Mechanical Description of Physical Reality Be Consider-
ed Complete?” Physical Review, Vol. 47, No. 10, 1935, p.
777. doi:10.1103/PhysRev.47.777
[2] R. Horodecki, P. Horodecki, M. Horodecki and K.
Horodecki, “Quantum Entanglement,” Reviews of Mod-
ern Physics, Vol. 81, No. 2, 2009, p. 865.
doi:10.1103/RevModPhys.81.865
[3] C. H. Bennett, G. B
and W. K. Wootters, “Tel
rassard, C. Crpeau, R. Jozsa, A. Peres
eporting an Unknown Quantum
State via Dual Classical and Einstein-Podolsky-
Channels,” Ph
Rosen
ysical Review Letters, Vol. 70, No. 13,
1993, p. 1895. doi:10.1103/PhysRevLett.70.1895
[4] Y. Yeo and W. K. Chua, “Teleportation and Dense Cod-
ing with Genuine Multipartite Entanglement,” Physical
Review Letters, Vol. 96, No. 6, 2006, Article ID: 060502.
doi:10.1103/PhysRevLett.96.060502
[5] G. Gordon and G. Rigolin, “Generalized Teleportation
Protocol,” Physical Review A, Vol. 73, No. 4, 2006, Arti-
cle ID: 042309. doi:10.1103/PhysRevA.73.042309
ol. 68
[6] L. Mista and R. Filip, “Optimal Partial Deterministic
Quantum Teleportation of Qubits,” Physical Review A,
Vol. 71, No. 4, 2005, Article ID: 022319.
[7] M. Fujii, “Continuous-Variable Quantum Teleportation
with a Conventional Laser,” Physical Review A, V,
No. 5, 2003, Article ID: 050302.
doi:10.1103/PhysRevA.68.050302
[8] D. Bouwmeester, J. Pan, K. Mattle, M. Eibl, H. Wein-
furter and A. Zeilinger, “Experimental Quantum Telepor-
tation,” Nature, Vol. 390, No. 6660, 1997, pp. 575-579.
doi:10.1038/37539
[9] P. M. Alsing, “Teleportation in a Non-Inertial Frame,”
Journal of Optics B: Quantum and Semiclassical Optics,
Vol. 6, No. 8, 2004, p. S834.
doi:10.1088/1464-4266/6/8/033
[10] P. M. Alsing and G. J. Milburn, “Teleportation with a
Uniformly Accelerated Partner,” Physical Review Letters,
Vol. 91, No. 18, 2003, Article ID: 180404.
doi:10.1103/PhysRevLett.91.180404
Detectors: From the Casimir? Polder
88/1464-4266/6/8/011
[11] M. R. Hwang, D. Park and E. Jung, “Tripartite Entangle-
ment in a Noninertial Frame,” Physical Review A, Vol. 83,
No. 1, 2001, Article ID: 012111.
[12] B. L. Hu, A. Roura and S. Shresta, “Vacuum Fluctuations
and Moving Atoms/
to the Unruh? Davies? DeWitt? Fulling Effect,” Journal
of Optics B: Quantum and Semiclassical Optics, Vol. 6,
No. 8, 2004, p. S698. doi:10.10
Entan-
2
[13] Q. Pan and J. Jing, “Degradation of Nonmaximal
glement of Scalar and Dirac Fields in Noninertial
Frames,” Physical Review A, Vol. 77, No. 2, 2008, Article
ID: 024302. doi:10.1103/PhysRevA.77.02430
z, “The Entangling
ssical Correlation and
[14] M. Montero and E. Martin-Martine
Side of the Unruh-Hawking Effect,” Journal of High En-
ergy Physics, Vol. 2011, No. 7, 2011, p. 6.
[15] J. Wang, J. Deng and J. Jing, “Cla
Quantum Discord Sharing of Dirac Fields in Noninertial
Frames,” Physical Review A, Vol. 81, No. 5, 2010, Article
ID: 052120. doi:10.1103/PhysRevA.81.052120
[16] J. Wang and J. Jing, “Multipartite Entanglement of Fer-
mionic Systems in Noninertial Frames,” Physical Review
A, Vol. 83, No. 2, 2011, Article ID: 022314.
doi:10.1103/PhysRevA.83.022314
[17] X. H. Ge and Y. G. Shen, “Teleportation in the Back-
ground of Schwarzschild Space? Time,” Physics Letters B,
Vol. 606, No.1-2, 2005, p. 184.
doi:10.1016/j.physletb.2004.11.067
[18] X. H. Ge and S. P. Kim, Class. “Quantum Entanglement
and Teleportation in Higher Dimensional Black Hole
Spacetimes,” Classical and Quantum Gravity, Vol. 25,
No. 7, 2008, Article ID: 075011.
doi:10.1088/0264-9381/25/7/075011
[19] X. H. Ge and Y. G. Shen, “Quantum Teleportation with
Sonic Black Holes,” Physics Letters B, Vol. 623, No. 1-2,
2005, p. 141. doi:10.1016/j.physletb.2005.07.036
iation, Entanglement, [20] Q. Pan and J. Jing, “Hawking Rad
and Teleportation in the Background of an Asymptoti-
cally Flat Static Black Hole,” Physical Review D, Vol. 78,
No. 6, 2008, Article ID: 065015.
doi:10.1103/PhysRevD.78.065015
[21] B. N. Esfahani, M. Shamirzai and M. Soltani, “Reduction
of Entanglement Degradation in Einstein-Gauss-Bonnet
gravity,” Physical Review D, Vol. 84, No. 2, 2011, Article
ID: 025024.
[22] D. Giulini, E. Joos, C. Kiefer, J. Kupsch, I. O. Stamatescu
. Haroche, “Observing
Meter in a Quantum
and H. D. Zeh, “Decoherence and the Appearence of a
Classical World in Quantum Teory,” Springer, Berlin,
1996, pp. 44-107.
[23] M. A. Schlosshauer, “Decoherence and the Quantum-to-
Classical Transition,” Springer, Berlin, 2007.
[24] M. Brune, E. Hagley, J. Dreyer, X. Maitre, A. Maali, C.
Wunderlich, J. M. Raimond and S
the Progressive Decoherence of the
Measurement,” Physical Review Letters, Vol. 77, No. 24,
1996, p. 4887. doi:10.1103/PhysRevLett.77.4887
[25] C. J. Myatt, B. E. King, Q. A. Turchette, C. A. Sackett, D.
Kiepinski, W. M. Itano, C. Monroc and D. J. Wineland,
“Decoherence of Quantum Superpositions through Cou-
pling to Engineered Reservoirs,” Nature, Vol. 403, No.
6767, 2000, p. 269. doi:10.1038/35002001

M. H. XIANG, J. L. JING 111
desso and I. Fuentes, “Optimal Quan-[26] M. Aspachs, G. A
tum Estimation of the Unruh-Hawking Effect,” Physical
Review Letters, Vol. 105, No. 15, 2010, Article ID:
151301. doi:10.1103/PhysRevLett.105.151301
[27] E. Martin-Martinez, L. J. Garay and J. Leon, “Unveiling
Quantum Entanglement Degradation near a Schwarzschild
Black Hole,” Physical Review D, Vol. 82, No. 6, 2010,
Article ID: 064006.
[28] E. Martin-Martinez, L. J. Garay and J. Leon, “Quantum
Entanglement Produced in the Formation of a Black
Hole,” Physical Review D, Vol. 82, No.6, 2010, Article
ID: 064028. doi:10.1103/PhysRevD.82.064028
[29] J. Wang and J. Jing, “System-Environment Dynamics of
X-Type States in Noninertial Frames,” Annals of Physics,
Vol. 327, No. 2, 2012, p. 283.
doi:10.1016/j.aop.2011.10.002
[30] A. Salles, F. de Melo, M. P. Almeida, M. Hor-Meyl
Entangle-
22
l, S. P.
Walborn, P. H. Souto Ribeiro and L. Davidovich, “Ex-
perimental Investigation of the Dynamics of
ment: Sudden Death, Complementarity, and Continuous
Monitoring of the Environment,” Physical Review A, Vol.
78, No. 2, 2008, Article ID: 022322.
doi:10.1103/PhysRevA.78.0223
[31] J. Maziero, L. C. Celeri, R. M. Serra and V. Vedral,
“Classical and Quantum Correlations under Decoher-
ence,” Physical Review A, Vol. 80, No. 4, 2009, Article
ID: 044102. doi:10.1103/PhysRevA.80.044102
[32] M. A. Nielsen and I. L. Chuang, “Quantum Computation
and Quantum Information,” Cambridg
Cambridge, 2000, pp. 425-427.
e University Press,
[33] J. Maziero, T. Werlang, F. Fanchini, L. C. Celeri and R.
M. Serra, “System-Reservoir Dynamics of Quantum and
Classical Correlations,” Physical Review A, Vol. 81, No.
2, 2010, Article ID: 022116.
doi:10.1103/PhysRevA.81.022116