Journal of Modern Physics, 2012, 3, 1958-1965
http://dx.doi.org/10.4236/jmp.2012.312244 Published Online December 2012 (http://www.SciRP.org/journal/jmp)
Charge Radius and Effective Couplings via the
Process vμe– → vμe–
A. Gutiérrez-Rodríguez1, M. A. Hernández-Ruíz2, Alejandro González-Sánchez1
1Facultad de Física, Universidad Autónoma de Zacatecas, Zacatecas, México
2Unidad Académica de Química, Universidad Autónoma de Zacatecas, Zacatecas, México
Received July 8, 2012; revised October 19, 2012; accepted October 26, 2012
ABSTRACT
In this work the neutral-current scattering cross-section for neutrinos on electrons is calculated assuming that a massive
Dirac neutrino is characterized by a phenomenological parameters, a charge radius 2 r and the right-handed currents
are present in the framework of a Left-Right symmetric model (LR). Using the CHARM II result for the charge radius
of the muon-neutrino 233
6.0 10cmr  2 , we place a bound on 33 2233 2 10 cm7.910 cm
LR
r

 7.9 . We
discuss the relationship between the electron neutral couplings e
V
g

and e
A
g

and the LR model parameters. We also
estimate a bound on the heavy massive neutral vector boson mass of the LR model. These results
have never been reported in the literature before and could have practical or theoretical interest, such as in the case of
the neutrinos produced in core-collapse supernova explosions, that is to say, right-handed Dirac neutrinos emission
from supernova core .
650 GeV
LR
ee 


R
Z
M
Keywords: Weak and Electromagnetic Interactions; Non-Standard-Model Neutrinos; Neutral Currents;
Electromagnetic Form Factors
1. Introduction
Although in the framework of the Standard Model (SM)
[1-3] neutrinos are assumed to be electrically neutral, the
electromagnetic properties of the neutrino are discussed
in many gauge theories beyond the SM. Electromagnetic
properties of the neutrino [4-8] may manifest themselves
in a non vanishing charge radius, thus the neutrino is
subject to the electromagnetic interaction.
The charge radius of e has been bounded by the
LAMPF [9] experiment
2272
7 10cm

0.9 2.r
obtaining, more recently LSND [10] limit from measure-
ment of electron-neutrino electron elastic scattering is
32 22
2.97 10cm4.
le
r

 32 2 14 10cm

,
while for the muon-neutrino the bound from the scatter-
ing experiment of CHARM II [11] is
2322
10 cm

0.6r.
To our knowledge, there are no bounds on the charge
radius of
 -neutrinos from scattering experiments. How-
ever, the corresponding bounds from Super-K and SNO
observations [12] for the neutrino charge radius are
2
r


,

2312
2.08 1.5310cmr




and

2322
6.865.2610cm .
e
r



Experimental evidence for neutrino flavor transforma-
tion [13] implies that neutrinos are the first elementary
particles whose properties cannot be fully described
within the SM. This hints to the possibility that other
properties of these intriguing particles might substan-
tially deviate from the predictions of the SM. As a result,
this has motivated vigorous efforts, both on the theoreti-
cal and experimental sides, to understand the detailed
properties of neutrinos and of their interactions more in
depth. In particular, electromagnetic properties of the
neutrinos can play important roles in a wide variety of
domains such as cosmology [14] and astrophysics [15,
16], and can play a role in the deficit of electron neu-
trinos from the sum [17-19].
In general, a photon may couple to charged leptons
C
opyright © 2012 SciRes. JMP

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1959
through its electric charge, magnetic dipole moment
(MM), electric dipole moment (EDM) and the anapole
moment (AM). This coupling may be parameterized us-
ing a matrix element in which the usual


is replaced
by a more general Lorentz-invariant form [4]:
 



22
22
5
QM
A
2
5 E
F
qFqiq
Fq qqq
 

Fqq





2

 
 (1)
where ,,
,
QMEA
F
q are the electromagnetic form fac-
tors of the neutrino, corresponding to the charge radius,
MM, EDM and AM, respectively.
Electromagnetic properties of neutrinos are of funda-
mental importance and serve as a probe of physics be-
yond the SM. Several authors have shown that the charge
radius of the neutrino is not a physical quantity [6,20], as
demonstrated by the fact that it is gauge-dependent [21].
However, other authors claim that they can extract a
gauge-independent neutrino charge radius, which is,
therefore, a physical observable [22]. A definition of the
neutrino charge radius that satisfies physical require-
ments, i.e. it is a physical observable, has recently been
provided [22] in the framework of the Pinch Technique
formalism [23].
In this paper, we start from a Left-Right symmetric
model (LR) [24] and assuming that a massive Dirac neu-
trino is characterized by a phenomenological parameter,
a charge radius 2
r

ee 


we calculate the cross-section of
the process

. We also estimate bounds on
the charge radius of the muon-neutrino in the framework
of the LR mode
33 22
7.9 10cm7
LR
r

 33 2 .9 10cm

,
using the limit of CHARM II for the charge radius of the
muon-neutrino 2332
0.6 10cm

r.
In a previous papers [25], possible corrections at the
couplings of the fermion with the gauge boson were cal-
culated, in particular the lepton couplings V
g
and A
g
with the neutral boson
L
Z
, which were measured with
great precision in LEP and CHARM II [11]. In the pre-
sent work, we calculate the simultaneous contribution of
the neutrino charge radius, the additional neutral vector
boson
R
Z
, the mixing angle

of the LR model on the
electron couplings constant


Ve
L
R
g

and

e
A
L
R
g

. We
also obtain bounds on the heavy massive neutral vector
boson mass
R
Z
M
of the LR model. The neutrino charge
radius in the LR model is simply treated as a new pa-
rameter. One is thus dealing with a purely phenomenol-
ogical analysis. For an analysis of the electromagnetic
form factors of the neutrino from a theoretical point of
view in Left-Right models, see [26].
This paper is organized as follows: in Section 2 we
carry out the calculus of the process . In
Section 3 we achieve the numerical computations and,
finally, we summarize our results in Section 4.
2. Muon-Neutrino Electron Cross-Section
In this section we obtain the corresponding amplitude for
the process




112 2
,kep kep



 (2)
mediated by the photon  and the neutral gauge bosons
L
Z
and
R
Z
. We assume that a massive Dirac neutrino
is characterized by a phenomenological parameter, a
charge radius 2
ree





. Therefore, the expression for the
cross-section of the process is given by


ee






22
22
22
2
22
2π2
122 ,
32
LR
T
Fe PS QR
GmE PS
PS QR
PS












 







(3)
where the neutrino charge radius, the heavy massive neu-
tral vector boson and the mixing angle

contribute to
the total cross-section. are given by ,,,PQRS





2,
,
,
2.
V
A
V
A
PABCg
QACg
RACg
SABCg

 
 

(4)
The constants A, B and C [27] depend only on the pa-
rameters of the LR model
22
22
22 22
22
22
2
2
,
,
,
,
2π,
3
L
R
WW
WW
WW WW
WW WW
WW
WW
Z
Z
F
ss
Ac scs
rr
sc sc
Bc sscsc
rr rr
cc
Cs c
rr
M
M
r
G
 
 








 



 











cosc

(5)
sins

cos
WW
c where ,




,

sin
WW
s,


,
cos 2
WW
r

 and
L
Z
M
,
Z
R
M
are the masses of the
light and heavy massive neutral vector bosons that par-
ticipate in the interaction.  together with  are the two
new parameters that are introduced in the LR model,
while 2 r is the charge radius of the muon-neutrino.
Bounds on this quantity are reported in the literature

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1960
[11,28,29]. We can in addition take the limit 0


and
2
Z and get the standard model cross-section.
Notice that it is not possible to factorize the neutrino
current in Equation (4), since P, Q, R and S are different,
and therefore we cannot parameterize the electron weak
coupling in terms of the effective couplings

M
eff
V

g
and
eff
A
g
.
2.1. Charge Radius of the Muon-Neutrino
From the cross-section expression (3), we obtain the in-
terference cross-section which is given by

,
E



,PS
2
2
3π
LR Fe
I
Gm

2PS (6)
where and

are defined in Equations (4) and
(5), respectively.
We rewrite the interference cross-section as the follow



22
11,
LR
IVA
VW AWAW
VA VA
Krg g
ga gbgb22
22
V
g
s
c
gg gg







 






(7)
where
4,
92
Fe
Gm E
K


 2,
W
,
WW
br
1
W
ar 22.
WW
br

0
Evaluating the limit when the mixing angle is


and R
Z,
M 0

, the second and third terms in
(7) is zero and Equation (7) is reduced to the expressions
(A.5, 17) given in Refs. [30,31]:

2
IVA
02 .
K
rgg   (8)
In order to identify the neutrino charge radius in the
LR model, of Equations (7) and (8), we define

22
2
12
2
1
2
VW
LR
VW
ga
rr
gagn
,
AW
VA
A W
VA
gb
gg
b
s
c












gg







 
(9)
where 2
L
R is the charge radius of the muon-neutrino
in the LR model and
r2
r is the charge radius in the
minimal extension of the standard model.
2.2. Electron Coupling Constants


e
V
L
R
g

and


e
A
L
R
g

In this subsection, the total cross-section Equation (3) is
written in such a way that we can express the theoretical
predictions for the electron couplings constant


e
V
L
R
g


e
A
and
L
R
g

such that give the SM couplings in the limit
0

 and :
R
Z
M


2
2
13
22
2
13 2
2
13
22
2
13 2
2
2
11
22
12
3
1,
2
LRe e Fe
TVA
ee ee
VA VA
ee
VA
ee ee
VA VA
GmE fg fg
fgfgf gg
fg fg
fgfgfgg
 
 

 







 

 




 

(10)


where

2
2222
123
2,1, ,
W
W
v
f
ufuvfvur
r

  (11)
and
sin
cos ,
W
ur

  cossin ,
W
vr

 

and with

as defined in Equation (5). We get the
SM [28] formula after taking 0, 0,



and
in Equation (10):
R
Z
M

222
1,
2π3
SMe ee e
Fe VA VA
GmE gg gg
 




 (12)




and by analogy with the standard model, likewise we have
 
2
22
2π
1.
3
LR Fe
T
ee ee
VA VA
LR LRLR LR
GmE
gg gg

 
 



 
 
(13)



 

eff
Using Equation (10) which includes the right-handed
current of the neutrino, we would obtain new limits on
the LR model parameters. We already mentioned in this
section that it was not possible at the amplitude level to
define V
g
and A
eff
g
for the electron couplings. How-
ever, looking at Equations (10) and (13) we see that this
is not the case for the total cross-section. As a matter of
fact we can identify the LR model couplings of the
electron in the following way:



2
3132
,,,,sin,
1
2
LR
ee
AZZ WA
LR
e
ASM
g
MM g
ffffg


 






 


(14)



2
3132
,,,,sin,
1
2
LR
ee
VZZ WV
LR
e
VSM
g
MM g
ffffg


 






0
(15)
In these expressions, with the limits


and
,
R
Z
M 0 the SM couplings are recovered.

3. Results
In this section, we present the numerical results obtained

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1961
for the charge radius of the muon-neutrino in the frame-
work of a Left-Right symmetric model 2
L
R
r, the elec-
tron couplings constants

e

e
AV
L
R
g

and
L
R
g

and of
the mass of the heavy massive neutral vector boson
. For the SM parameters, we adopted the following:
M
Z
R
91.187
L
Z
M00.007 GeV
0.2312  e and W [28]. At the present time, the
most precise direct measurements of ,VA
2
sin
g

0.035 0.017
0.5030.017
1
come from
the LEP and CHARM II experiments [11,28]
e
V
g


and 2
LR
rFigure 2. Allowed region for as a function of the
mixing angle φ with the value
e
A
g

 2 r. The dashed line shows
the allowed region for at

in agreement with the SM and the world average
values. For the mixing angle

between
2
r, while the dotted line shows the
same result for the LR model.
L
Z
and
R
Z
,
we use the reported data in [32-34]:
2
r
analysis was done using the experimental value for
reported by CHARM II [11] with a 90% C.L. In the same
figure, we show the
33
1.22 10,

 1.66 10    (16)
with 90% C.L. Other limits on the mixing angle

re-
ported in the literature are given in [35,36].
2
r

0   result at 90% C.L.
with the dashed horizontal lines. The allowed region In
the LR model (dotted line) for
In order to estimate a limit on the charge radius of the
muon-neutrino
2
2
L
R in the framework of the Left-
Right symmetric model, we plot the expression (9) to
analyze the general behavior of the
r
L
R
r is wider than the
one for the 2 r, and is given by:
33 22
33 2
7.9 10cm
7.910cm,90% C.L.
LR
r


 

2
L
Rfunction
(Figure 1). In this figure, we observe that the mixing
angle
r

, around –0.75 rad, 2
L
R can be as high as
10.4, and for values of
(17)
rwhose value is quite close to that reported by other au-
thors [5,6,8,11,12,28,29].
2

around 0.8 rad,
L
R is as
low as 5.5. This shows a strong dependence on
r

; there-
fore, if 2
L
R is the charge radius, the restriction on
the charge radius can be “softened” if we consider a LR
model. In Figure 2, we show the allowed region for
2
Figure 3 shows the charge radius
L
R as a func-
tion of the LR parameters
r
r

and
R
Z
M
. This figure
shows a strong dependence of the charge radius with
respect to the model parameters. In Figure 4 we plot 2

as a function of
2
r
L
R as a function of

with 90\% C.L. The allowed
region is the rectangle band that is a result of both factors
in Equation (9). In this figure, the second factor gives the
rectangle band while

and
Z
R
M
. The minimum is obtained
for 3 1.22 10 

 800 GeV
23
1.78 10 
and R
Z
M with


e
A

. In Figure 5 we have plotted
2
r gives the bandwidth. This
L
R
g

from Equation (14) as a function of the LR parameters

and
Z
R
M
. We have chosen the range
33
1.66 101.22 10 


  300800 GeV
L
Z
M and
where

is measured in radians.
In Figure 6 we have plotted V

e
L
Rfrom Equation
(15) as a function of
g


and
R
Z
M
. The range of varia-
tion for the LR parameters is the same as in Figure 5. In
this case the experimental value, VLR is
reached for small values of

exp 0.035g
M
and

. The effect of
Z
R


e
A
Figure 1. 2
LR
r as a function of the mixing angle

.
these two variables on
L
R
g


e
V
and

L
R
g

2
is similar.
In Figure 7 we plot

as a function of the LR pa-
rameters taking the same range of variation. The minimum
is obtained for and R
Z.
with
3
1.22 10 

 800 GeVM
25
3.85 10 

 2 . In Figure 8 we plot

, the
minimum is obtained for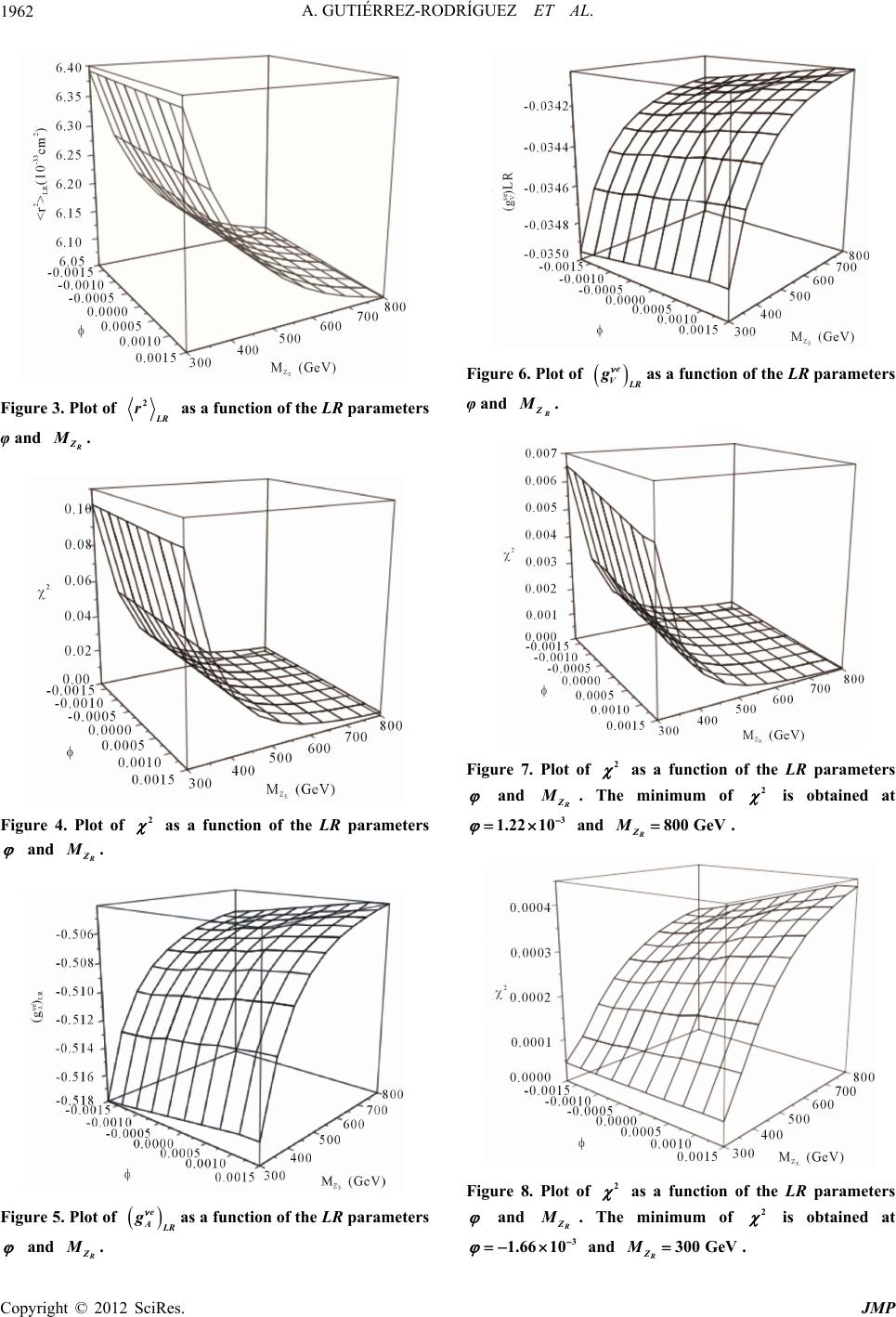

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1962


Figure 3. Plot of 2
LR
r as a function of the LR parameters
φ and
R
Z
M.
Figure 4. Plot of 2

as a function of the LR parameters

and
R
Z
M.
Figure 5. Plot of


e
ALR
g

as a function of the LR parameters

and
R
Z
M.
Figure 6. Plot of e
VLR
g

as a function of the LR parameters
φ and
R
Z
M.
Figure 7. Plot of 2

as a function of the LR parameters

and
R
Z
M2 . The minimum of

is obtained at
3
1.22 10 

 800 GeV
R
Z
M and

.
Figure 8. Plot of 2

as a function of the LR parameters

and
R
Z
M2 . The minimum of

is obtained at
3
1.66 10 

  300 GeV
R
Z
M and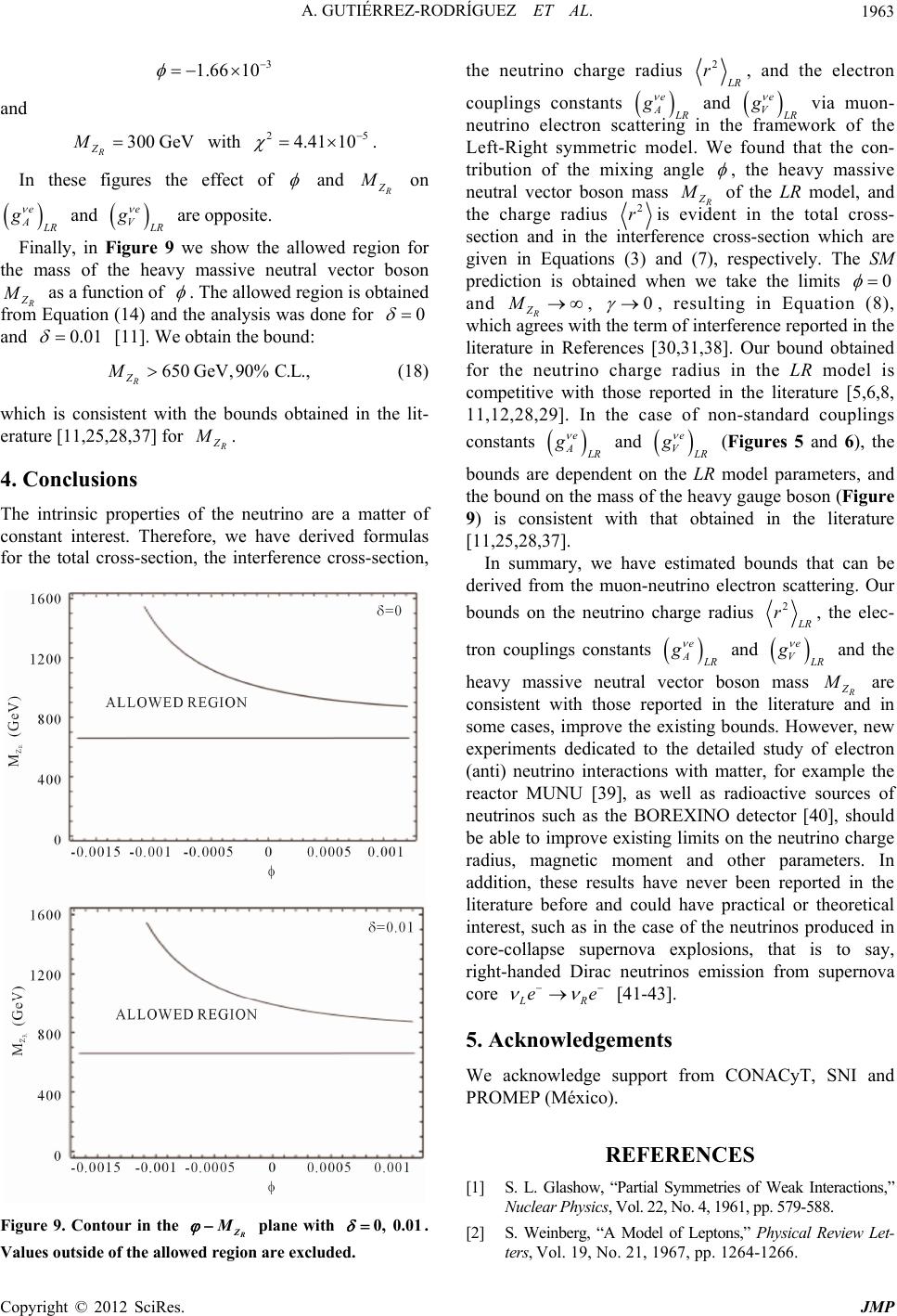

.

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1963
3
1.66 10  
30
R25
4.41 10
2

and
0 GeV 
Z
M with

.
In these figures the effect of

and
R
Z
M
on

e
A
L
R
g

and

e
V
L
R
g

are opposite.
Finally, in Figure 9 we show the allowed region for
the mass of the heavy massive neutral vector boson
R
Z
M
as a function of

. The allowed region is obtained
from Equation (14) and the analysis was done for 0


and 0.01


,90% C.L.,
[11]. We obtain the bound:
650 GeV
R
Z
M (18)
which is consistent with the bounds obtained in the lit-
erature [11,25,28,37] for
R
Z
M
.
4. Conclusions
The intrinsic properties of the neutrino are a matter of
constant interest. Therefore, we have derived formulas
for the total cross-section, the interference cross-section,
Figure 9. Contour in the
R
Z
M

 0,0.01 plane with


.
Values outside of the allowed region are excluded.
the neutrino charge radius
L
R
r, and the electron
couplings constants


e
A
L
R and V
g


e
L
R via muon-
neutrino electron scattering in the framework of the
Left-Right symmetric model. We found that the con-
tribution of the mixing angle
g


, the heavy massive
neutral vector boson mass
R
Z
M
of the LR model, and
the charge radius 2 r
0
is evident in the total cross-
section and in the interference cross-section which are
given in Equations (3) and (7), respectively. The SM
prediction is obtained when we take the limits


and R
Z,
M 0

, resulting in Equation (8),
which agrees with the term of interference reported in the
literature in References [30,31,38]. Our bound obtained
for the neutrino charge radius in the LR model is
competitive with those reported in the literature [5,6,8,
11,12,28,29]. In the case of non-standard couplings


e
A


e
V
constants
L
R
g

and
L
R
g

(Figures 5 and 6), the
bounds are dependent on the LR model parameters, and
the bound on the mass of the heavy gauge boson (Figure
9) is consistent with that obtained in the literature
[11,25,28,37].
In summary, we have estimated bounds that can be
derived from the muon-neutrino electron scattering. Our
2
bounds on the neutrino charge radius
L
R
r, the elec-


e
A
tron couplings constants
L
R
g


e
V
and
L
R
g

and the
heavy massive neutral vector boson mass
R
Z
M
are
consistent with those reported in the literature and in
some cases, improve the existing bounds. However, new
experiments dedicated to the detailed study of electron
(anti) neutrino interactions with matter, for example the
reactor MUNU [39], as well as radioactive sources of
neutrinos such as the BOREXINO detector [40], should
be able to improve existing limits on the neutrino charge
radius, magnetic moment and other parameters. In
addition, these results have never been reported in the
literature before and could have practical or theoretical
interest, such as in the case of the neutrinos produced in
core-collapse supernova explosions, that is to say,
right-handed Dirac neutrinos emission from supernova
core LR
ee 


 [41-43].
5. Acknowledgements
We acknowledge support from CONACyT, SNI and
PROMEP (México).
REFERENCES
[1] S. L. Glashow, “Partial Symmetries of Weak Interactions,”
Nuclear Ph ysics , Vol. 22, No. 4, 1961, pp. 579-588.
[2] S. Weinberg, “A Model of Leptons,” Physical Review Let-
ters, Vol. 19, No. 21, 1967, pp. 1264-1266.

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1964
[3] N. Svartholm, “Elementary Particle Theory,” Almqvist
and Wiskell, Stockholm, 1968.
[4] B. Kayser, “Majorana Neutrinos and their Electromagnetic
Properties,” Physical Review D, Vol. 26, No. 11, 1982, pp.
1662-1670. doi:10.1103/PhysRevD.26.1662
[5] G. Degrassi, A. Sirlin and W. J. Marciano, “Effective
Electromagnetic Form-Factor of the Neutrino,” Physical
Review D, Vol. 39, No. 1, 1989, pp. 287-294.
doi:10.1103/PhysRevD.39.287
[6] J. L. Lucio, A. Rosado and A. Zepeda, “A Characteristic
Size for the Neutrino,” Physical Review D, Vol. 31, No. 5,
1985, pp. 1091-1096. doi:10.1103/PhysRevD.31.1091
[7] C. Giunti and A. Studenikin, “Neutrino Electromagnetic
Properties,” Physics of Atomic Nuclei, Vol. 72, No. 12,
2009, pp. 2089-2125. doi:10.1134/S1063778809120126
[8] K. J. F. Gaemers, R. Gandhi and J. M. Lattimer, “Neu-
trino Helicity Flips via Electroweak Interactions and
SN1987a,” Physical Review D, Vol. 40, No. 5, 1989, pp.
309-314. doi:10.1103/PhysRevD.40.309
[9] R. C. Allen, H. H. Chen, P. J. Doe, R. Hausammann, W.
P. Lee, X. Q. Lu, H. J. Mahler and M. E. Potter, “Study of
Electron-Neutrino Electron Elastic Scattering at LAMPF,”
Physical Revi ew D, Vol. 47, No. 1, 1993, pp. 11-28.
doi:10.1103/PhysRevD.47.11
[10] L. B. Auerbach, et al., “Measurement of Electron-Neutrino
and Electron Elastic Scattering,” Physical Review D, Vol. 63,
2001, Article ID: 112001.
doi:10.1103/PhysRevD.63.112001
[11] P. Vilain, et al., “Experimental Study of Electromagnetic
Properties of the Muon-Neutrino in Neutrino-Electron
Scattering,” Physics Letters B, Vol. 345, No. 1, 1995, pp.
115-118. doi:10.1016/0370-2693(94)01678-6
[12] A. S. Joshipura and S. Mohanty, “Bounds on Tau Neutrino
Magnetic Moment and Charge Radius from Super-K and
SNO Observations,” arXiv:hep-ph/0108018.
[13] T. Toshito, “Super-Kamiokande Atmospheric Neutrino
Results,” arXiv:hep-ex/0105023.
[14] A. D. Dolgov, “Neutrinos in Cosmology,” Physics Reports,
Vol. 370, No. 4-5, 2002, pp. 333-535.
doi:10.1016/S0370-1573(02)00139-4
[15] R. N. Mohapatra and P. B. Pal, “Massive Neutrinos in
Physics and Astrophysics,” 3rd Edition, World Scientific,
Singapore City, 2004. doi:10.1142/9789812562203
[16] A. Cisneros, “Effect of Neutrino Magnetic Moment on Solar
Neutrino Observations,” Astrophysics and Space Science,
Vol. 10, No. 10, 1971, pp. 87-92. doi:10.1007/BF00654607
[17] J. Pulido, “Solar Neutrinos with Magnetic Moment: Rates
and Global Analysis,” Astroparticle Physics, Vol. 18, No.
2, 2002, pp. 173-181.
doi:10.1016/S0927-6505(02)00106-8
[18] J. Pulido and E. K. Akhmedov, “Resonance Spin Flavor
Precession and Solar Neutrinos,” Astroparticle Physics,
Vol. 13, No. 2-3, 2000, pp. 227-244.
doi:10.1016/S0927-6505(99)00121-8
[19] M. M. Guzzo and H. Nunokawa, “Current Status of the
Resonant Spin Flavor Precession Solution to the Solar
Neutrino Problem,” Astroparticle Physics, Vol. 12, No.
1-2, 1999, pp. 87-95.
doi:10.1016/S0927-6505(99)00075-4
[20] W. A. Bardeen, R. Gastmans and B. E. Lautrup, “Static
Quantities in Weinberg’s Model of Weak and Electromag-
netic Interactions,” Nuclear Physics B, Vol. 46, No. 1, 1972,
pp. 319-331. doi:10.1016/0550-3213(72)90218-0
[21] B. W. Lee and R. E. Shrock, “Natural Suppression of
Symmetry Violation in Gauge Theories: Muon-Lepton and
Electron Lepton Number Non-Conservation,” Physical Re-
view D , Vol. 16, No. 5, 1977, pp. 1444-1473.
doi:10.1103/PhysRevD.16.1444
[22] J. Bernabeu, J. Papavassiliou and J. Vidal, “On the Ob-
servability of the Neutrino Charge Radius,” Physical Re-
view Letters, Vol. 89, No. 2002, Article ID: 101802.
doi:10.1103/PhysRevLett.89.101802
[23] J. M. Cornwall and J. Papavassiliou, “Gauge Invariant
Three-Gluon Vertex in QCD,” Physical Review D, Vol.
40, No. 10, 1989, pp. 3474-3485.
doi:10.1103/PhysRevD.40.3474
[24] J. C. Pati and A. Salam, “Lepton Number as the Fourth
Color,” Physical Review D, Vol. 10, No. 1, 1974, pp. 275-
289. doi:10.1103/PhysRevD.10.275
[25] M. Czakon, J. Gluza and M. Zralek, “Low-Energy Physics
and Left-Right Symmetry: Bounds and the Model Pa-
rameters,” Physics Letters B, Vol. 458, No. 2-3, 1999, pp.
355-360. doi:10.1016/S0370-2693(99)00567-5
[26] G. C. Branco and J. Liu, “More on the Neutrino Magnetic
Moment in Left-Right Models,” Physics Letters B, Vol.
210, No. 1-2, 1988, pp. 164-168.
doi:10.1016/0370-2693(88)90366-8
[27] V, Cerón, M. Maya and O. G. Miranda, “Particles and
Fields,” World Scientific, Singapore City, 1994.
[28] Particle Data Group, C. Amsler, et al., “Review of Parti-
cle Physics,” Physics Letters B, Vol. 667, No. 1-5, 2008,
p. 1
[29] M. Hirsch, E. Nardi and D. Restrepo, “Bounds on the Tau
and Muon Neutrino Vector and Axial Vector Charge Ra-
dius,” Physical Review D, Vol. 67, No. 3, 2003, Article
ID: 033005. doi:10.1103/PhysRevD.67.033005
[30] P. Vogel and J. Engel, “Neutrino Electromagnetic Form-
Factors,” Physical Review D, Vol. 39, No. 11, 1989, pp.
3378-3383. doi:10.1103/PhysRevD.39.3378
[31] J. Dorenbosch, et al., “Experimental Results on Neutrino-
Electron Scattering,” Zeitschrift für Physik C: Particles and
Fields, Vol. 41, No. 4, 1989, pp. 567-589.
doi:10.1007/BF01564701
[32] A. Gutierrez-Rodriguez, M. A. Hernandez-Ruiz and M. A.
Perez, “Limits on the Electromagnetic and Weak Dipole
Moments of the Tau-Lepton in E(6) Superstring Models,”
International Journal of Modern Physics A, Vol. 22, No.
20, 2007, p. 3493.
[33] A. Gutierrez-Rodriguez, M. A. Hernandez-Ruiz, M. A. Perez
and F. Perez-Vargas, “Bounding the Number of Light Neu-
trinos Species in a Left-Right Symmetric Model,” hep-ph/
0702076.
[34] A. Gutierrez-Rodriguez, M. A. Hernandez-Ruiz, M. A.
Perez and F. Perez-Vargas, “Constraints on Left-Right
Symmetric and E(6) Superstring Models from the Num-

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1965
ber of Light Neutrino Species,” Modern Physics Letters A,
Vol. 24, No. 2, 2009, p. 135.
[35] O. Adriani, et al., “Search for a Z′ at the Z Resonance,”
Physics Letters B, Vol. 306, No. 1-2, 1993, pp. 187-196.
doi:10.1016/0370-2693(93)91156-H
[36] M. Maya and O. G. Miranda, “Constraints on Z1-Z2 Mixing
from the Decay Z1→e−e+ in the Left-Right Symmetric
Model,” Zeitschrift für Physik C: Particles a nd Fi el d s, Vol.
68, No. 3, 1995, pp. 481-484. doi:10.1007/BF01620725
[37] J. Polak and M. Zralek, “Left-Right Symmetric Model
Parameters: Updated Bounds,” Physical Review D, Vol.
46, No. 9, 1992, pp. 3871-3875.
doi:10.1103/PhysRevD.46.3871
[38] P. Salati, “The Laboratory and Astrophysical Constraints
on the Neutrino Charge Radius,” Astroparticle Physics,
Vol. 2, No. 3, 1994, pp. 269-290.
doi:10.1016/0927-6505(94)90006-X
[39] C. Broggini, “The MUNU Experiment on Low Energy
Anti-Nu/E Scattering,” Nuclear Physics B—Proceedings
Supplements, Vol. 110, No. 2, 2002, pp. 398-400.
doi:10.1016/S0920-5632(02)80164-5
[40] A. Ianni, D. Montanino and G. Scioscia, “Test of Non-
Standard Neutrino Properties with the Borexino Source Ex-
periments,” European Physical Journal C, Vol. 8, No. 4,
1999, pp. 609-617.
[41] K. Fujikawa and R. Shrock, “The Magnetic Moment of a
Massive Neutrino and Neutrino Spin Rotation,” Physical
Review Letters, Vol. 45, No. 12, 1980, pp. 963-966.
doi:10.1103/PhysRevLett.45.963
[42] O. Lychkovskiy, “Neutrino Magnetic Moment Signatures
in the Supernova Neutrino Signal,” Trudi 51oi Nauchnoi
Konferencii MFTI, Chast II, Moscow-Dolgoprudny, 2008,
p. 90 (in Russian).
[43] A. V. Kuznetsov, N. V. Mikheev and A. A. Okrugin,
“Reexamination of a Bound on the Dirac Neutrino Magnetic
Moment from the Supernova Neutrino Luminosity,” Inter-
national Journal of Modern Physics A, Vol. 24, No. 31,
2009, p. 5977. doi:10.1142/S0217751X09047612