Optics and Photonics Journal, 2012, 2, 344-351
http://dx.doi.org/10.4236/opj.2012.24043 Published Online December 2012 (http://www.SciRP.org/journal/opj)
Analysis of As2S3-Ti: LiNbO3 Taper Couplers Using
Supermode Theory
Xin Xia, Yifeng Zhou, Christi K. Madsen
Department of Electrical and Computer Engineering, Texas A&M University, College Station, USA
Received October 16, 2012; revised November 14, 2012; accepted November 24, 2012
ABSTRACT
In this work, we develop a simulation method based on supermode theory and transfer matrix formalism, and then apply
it to the analysis and design of taper couplers for vertically integrated As2S3 and Ti: LiNbO3 hybrid waveguides. Test
structures based on taper couplers are fabricated and characterized. The experimental results confirm the validity of the
modeling method, which in turn, is used to analyze the fabricated couplers.
Keywords: Optical Waveguides; Couplers; Coupled Mode Analysis
1. Introduction
As study on integrated Optics proceeds, several schemes
with regard to materials and structures were developed,
such as silicon-on-insulator, chalcogenide glass wave-
guides, III-V semiconductor waveguides and titanium
diffused waveguides. While different schemes have their
own merits and shortcomings, reciprocal benefits can be
obtained from integration of them, namely, the hybrid
waveguides. For example, preliminary result was re-
ported on As2S3-on-Ti: LiNbO3 hybrid waveguide de-
vices [1,2], which benefit from the high index contrast of
As2S3 and easy connection with commercial single mode
fibers. For integration of different waveguides, light cou-
pling is the key. A directional coupler is the simplest
functional device to couple light by transferring energy
between two waveguides. However, in practice its cou-
pling efficiency can be fairly low due to the phase mis-
match and small tolerance to fabrication errors. Alterna-
tively grating and taper couplers are used, and taper cou-
plers are generally preferred owing to its simplicity in
design and fabrication. Despite diverse forms, the general
taper coupler is composed of two parallel waveguides
placed in close proximity: one is uniform whereas at one
end of the other one, the width is gradually varied. Two
ends of the taper match the wave guiding properties of
two waveguides, so the mode is transformed gradually
from one into another during propagation in the taper.
Although the principle is intuitively quite simple, the
design in most cases is conservative because of the lack
of precise modeling guidelines and accurate modeling
tools [3]. A lot of theoretical study was carried out to
investigate them, and different approaches were devel-
oped. Lee et al. proposed an equivalent waveguide con-
cept employing a conformal mapping method, which was
combined with the Beam Propagation Method (BPM) to
conduct analysis [4]. In [3], tapered waveguides were
analyzed by considering the whole taper as a succession
of short linear taper fragments and modeling each of
them using a two-dimensional BPM that solves directly
the Helmholtz equation.
However, most of the early work focused on correct-
ing simulation methods to improve the accuracy, and the
underlying physical mechanism governing the power
transfer was not described [5]. Therefore, few guidelines
can be found for designers. Thus more and more re-
searchers began to look into taper couplers from the an-
gle of supermodes, i.e. local modes. In [5], Xia et al. de-
fined and distinguished between the resonant coupling
and adiabatic coupling from the view of supermodes [5].
Resonant couplers are compact and simple but highly
sensitive to unavoidable variations during fabrication [5].
Adiabatic couplers , on the contrary, don’t require exact
control of taper length and gap, but need longer lengths
[6]. Sun et al. conducted a series of studies on the be-
havior of supermodes in adiabatic couplers [6,7] and
derived a mathematical expression of the shortest adia-
batic tapers [6]. As such theoretical work contributed a
lot to our understanding of taper couplers, the study on
issues of practical application and modeling is still lack-
ing. In practice, we often need to balance the taper length
and the coupling efficiency, since we may not have suf-
ficient space to fulfill the adiabatic condition, and we
may want certain coupling efficiency that is not neces-
sarily 100%. Mach-Zehnder interference filters, for ex-
ample, typically use 3 dB couplers. Moreover, the mate-
C
opyright © 2012 SciRes. OPJ

X. XIA ET AL. 345
rials and structures used may limit the coupling. Thus,
there are a lot of efficient but non-adiabatic taper cou-
plers desired in practice.
In published papers most simulations were conducted
based on beam propagation method (BPM) [8]. BPM
calculates the electromagnetic fields during light propa-
gation process and gives distributions of electric and
magnetic fields. It is highly accurate as long as certain
assumptions are met. However, limited knowledge of
underlying mechanism can be obtained from the simula-
tion process, so it is widely used to as a means of exam-
ining the designed taper coupler instead of guiding the
design at the first place. Alternatively, the modeling of
taper couplers can be based on the concept of modes us-
ing the coupled mode theory, which can provide insights
to the mode evolvement in the coupler and thus provide
immediate guidelines for design.
2. Modeling Methods
A taper coupler, which consists of two adjacent wave-
guides, can be regarded as a modified directional coupler.
In each waveguide, only one mode is allowed to propa-
gate. The coupled mode theory analyzes the coupled
waveguides by taking one waveguide as the subject and
studying the influence of the perturbation imposed by the
presence of the other one. The supermode theory, how-
ever, views the coupled waveguides as a whole system,
i.e. a composite two-waveguide structure, and studies the
normalized local modes of the system, which are called
supermodes. Nevertheless, both theories describe mode
coupling for scenarios that coupled waveguides are in-
variable along the propagation direction. But the taper
coupler is a varying structure where the width of one of
the waveguides is constantly changing along the propa-
gation direction. However, the coupler can be divided
into a succession of infinitely short sections. The length
of each section is so small that the width can be regarded
as invariant. So the simulation of a taper coupler can be
divided into two steps: modeling of individual divisions
and a cascade of individual models. For each division, as
the width is deemed constant, it is actually a simple di-
rectional coupler, in which there are fundamental super-
mode and first order supermode, named as even mode
(Ee) and odd mode (Eo) respectively according to the
symmetry of their field distributions. The total field is a
linear combination of the even and odd mode.
If the propagation constants of modes in indivi-
dual waveguides are the same, namely, they are phase
matched, two lobes of even and odd mode have the same
size. If two propagation constants are different, that is,
the phases are mismatched, the symmetry of lobes of Ee
and Eo is broken, and their shapes are different. When
phase mismatch is large, two waveguides are effectively
decoupled: a wave propagating in either one is virtually
unaffected by the existence of the other, and the super-
modes of the composite structure just become those of
the individual waveguides [9]. δ is defined as the differ-
ence of the propagation constants of two individual
modes while βc is for two supermodes in a similar way in
(1):
21
and
22
eo
c

 

 

(1)
As shown in Figure 1, if δ is much smaller than 0,
most energy of the even mode is located in waveguide 1
while if it is much larger than 0, most energy is located in
waveguide 2. The opposite is true for the odd mode. So,
the essence of taper coupling is to spatially transfer the
energy of a supermode (even mode) from one waveguide
to the other by designing the tapered waveguide so that δ
sweeps from a negative value to a positive value while
suppressing the coupling to the other supermode (odd
mode) [6]. The larger scope δ covers, the more thorough
the energy transfer is. Ideally, δ changes from negative
infinity to positive infinity, whereas in practice, the scope
is determined by the materials and structures.
Solving the coupled mode equations by substituting
the general supermode solutions into them, we can obtain
the expressions of supermodes and the relationship be-
tween the phase mismatch of supermodes (βc) and that of
individual modes (δ) [7]
22
c
2



 (2)
As δ and βc are known, the coupling strength κ [9] can
be calculated. Then we have a complete mathematical
description of the model with parameter δ, κ and βc. Fol-
lowing the same method, models of all the divisions in
the taper coupler can be built.
Subsequently, transfer matrix formalism is derived to
cascade all the models based on coupled mode equations.
In the matrix form, the solution to coupled mode equa-
tions is (3).


 
 
 


1i
2
i
1 i
2
cossin e
sin esin e
0
cossin e0
z
cc
c
iz z
cc
cc
z
cc
c
Ez j
zz
Ez
jj
zz
E
j
zz
E














 



 

 



 



 
(3)
where


10E and


20E are the input electric fields in
waveguide 1 and 2 respectively. Let 0 and re-form
the equation to obtain the expression of vector, let
0
zz
zz z

 to re-write (3), substitute the vector expres-
sion into it, and we arrive at the transfer matrix formal-
ism relating the model at to the model at
0
zz

X. XIA ET AL. 346
0
z in (4).




 
 





 

00
00
10
20
10
00 00
20
i
i
i
i
;
cossin e
sin e
sin e
cossin e
z
cc
c
zzz
c
c
zzz
c
c
z
cc
c
Ez z
Ez z
Ez ;
M
zzz Mzzz
Ez
j
zz
jz
jz
j
zz


















  


 




 



 







 




(4)
starts with uncoupled waveguides, and their eigen-modes
are computed individually without the presence of the
other one. The propagation constants of the Ti waveguide
mode and the As2S3 waveguide mode are found to be β1
and β2 respectively. Then the model for the coupled sys-
tem is built, and the even mode (βe) and odd mode (βo)
are found, as Figure 2 shows.
Figure 1. The supermodes of a taper coupler.
Then by multiplying the matrices in order, the models
are cascaded. As a result, the electric field at certain
point can be obtained from the known input
z


10E
and . The algorithm is summarized in Table 1.

2
E

0
Table 1. Algorithm of modeling the taper coupler.
1Discretize the taper coupler into a sequence of sufficiently
small divisions;
2
Regard each section as a directional coupler and model
it to obtain mode propagation constants β1, β2, βe and βo,
and compute δ, βc and κ;
3Calculate individual transfer matrix of each division
based on parameter δ, βc and κ;
4Cascade all the divisions together by multiplying
matrices in order;
5Calculate the coupling efficiency.
In step 2, due to the complexity of the waveguide
structure, computer software FIMMWAVE (Photon De-
sign Ltd.) is used to model each section, i.e., to compute
mode parameters. The film mode matching method is
applied as the mode solver. It is good for structures con-
sisting of large uniform areas, such as As2S3 rectangular
waveguides. The resolution and the size of simulation
window are tested to prevent artificial errors. Simulation
Figure 2. The fundamental mode of the Ti waveguide (a) and the As2S3 waveguide (b) and the odd (c) and even mode (d) of
coupled waveguides.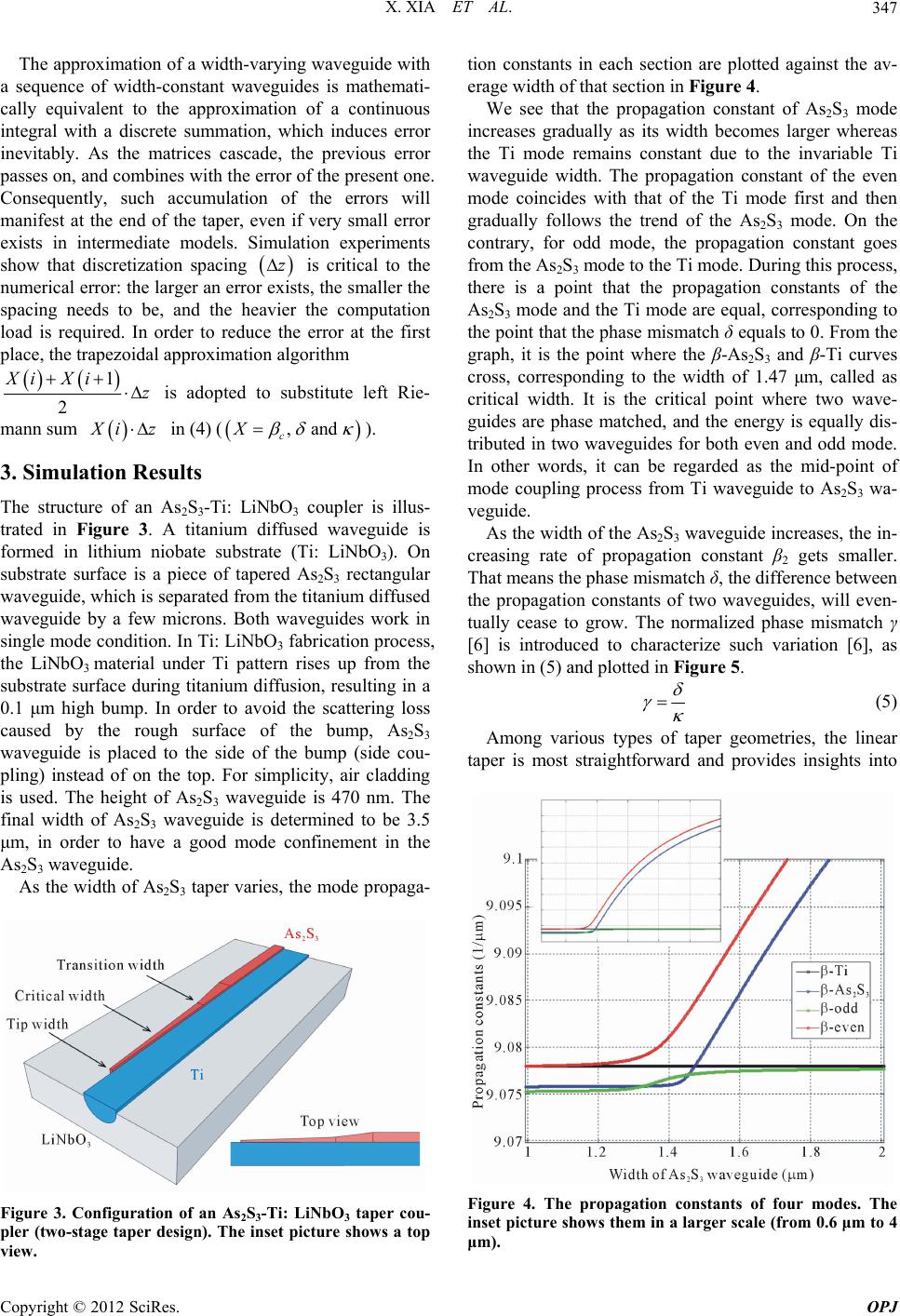

X. XIA ET AL. 347
The approximation of a width-varying waveguide with
a sequence of width-constant waveguides is mathemati-
cally equivalent to the approximation of a continuous
integral with a discrete summation, which induces error
inevitably. As the matrices cascade, the previous error
passes on, and combines with the error of the present one.
Consequently, such accumulation of the errors will
manifest at the end of the taper, even if very small error
exists in intermediate models. Simulation experiments
show that discretization spacing is critical to the
numerical error: the larger an error exists, the smaller the
spacing needs to be, and the heavier the computation
load is required. In order to reduce the error at the first
place, the trapezoidal approximation algorithm

z
 
1
2
Xi Xiz 
 is adopted to substitute left Rie-
mann sum

X
iz in (4) (


,and
c
X

 ).
3. Simulation Results
The structure of an As2S3-Ti: LiNbO3 coupler is illus-
trated in Figure 3. A titanium diffused waveguide is
formed in lithium niobate substrate (Ti: LiNbO3). On
substrate surface is a piece of tapered As2S3 rectangular
waveguide, which is separated from the titanium diffused
waveguide by a few microns. Both waveguides work in
single mode condition. In Ti: LiNbO3 fabrication process,
the LiNbO3 material under Ti pattern rises up from the
substrate surface during titanium diffusion, resulting in a
0.1 μm high bump. In order to avoid the scattering loss
caused by the rough surface of the bump, As2S3
waveguide is placed to the side of the bump (side cou-
pling) instead of on the top. For simplicity, air cladding
is used. The height of As2S3 waveguide is 470 nm. The
final width of As2S3 waveguide is determined to be 3.5
μm, in order to have a good mode confinement in the
As2S3 waveguide.
As the width of As2S3 taper varies, the mode propaga-
Figure 3. Configuration of an As2S3-Ti: LiNbO3 taper cou-
pler (two-stage taper design). The inset picture shows a top
view.
tion constants in each section are plotted against the av-
erage width of that section in Figure 4.
We see that the propagation constant of As2S3 mode
increases gradually as its width becomes larger whereas
the Ti mode remains constant due to the invariable Ti
waveguide width. The propagation constant of the even
mode coincides with that of the Ti mode first and then
gradually follows the trend of the As2S3 mode. On the
contrary, for odd mode, the propagation constant goes
from the As2S3 mode to the Ti mode. During this process,
there is a point that the propagation constants of the
As2S3 mode and the Ti mode are equal, corresponding to
the point that the phase mismatch δ equals to 0. From the
graph, it is the point where the β-As2S3 and β-Ti curves
cross, corresponding to the width of 1.47 μm, called as
critical width. It is the critical point where two wave-
guides are phase matched, and the energy is equally dis-
tributed in two waveguides for both even and odd mode.
In other words, it can be regarded as the mid-point of
mode coupling process from Ti waveguide to As2S3 wa-
veguide.
As the width of the As2S3 waveguide increases, the in-
creasing rate of propagation constant β2 gets smaller.
That means the phase mismatch δ, the difference between
the propagation constants of two waveguides, will even-
tually cease to grow. The normalized phase mismatch γ
[6] is introduced to characterize such variation [6], as
shown in (5) and plotted in Figure 5.




(5)
Among various types of taper geometries, the linear
taper is most straightforward and provides insights into
Figure 4. The propagation constants of four modes. The
inset picture shows them in a larger scale (from 0.6 μm to 4
μm).

X. XIA ET AL. 348
the general taper design. Figure 6 shows the coupling
efficiency of linear tapers of different lengths, with width
varying from 1.0 μm to 3.5 μm.
The squares stand for the coupling efficiency and the
bars represent the magnitude of oscillation. There is an
optimum point that the maximum coupling efficiency
reaches 96% when the length is 5 mm. The inset curve
shows the percentage of energy coupled as light propa-
gates through a 5 mm long linear taper. We can see that it
consists of a monotonically ascending part and a subse-
quent oscillation part. The coupling is mostly contributed
by the former part while the latter is due to resonance
effects.
For the even mode, the larger γ is, the more energy is
located in As2S3 waveguide and the less in Ti waveguide,
while it is vice versa for the odd mode. Since the even
mode is the mode to couple, the energy remaining in Ti
Figure 5. γ of the As2S3-Ti: LiNbO3 coupler.
Figure 6. Coupling efficiency for tapers of different length,
with the inset figure showing the coupling process of a 5
mm long taper, i.e., the coupling efficiency versus the loca-
tion along the taper.
waveguide imposes an ultimate limit to the coupling ef-
ficiency. From the curve of γ in Figure 5, we learn that at
the end of the taper, γ is 2.59. Because γ is not large
enough, there is still a coupling between two waveguides.
Such coupling deteriorates the coupling efficiency and
causes it to oscillate. The behavior of the coupler in this
region is similar to that of a resonant coupler. As a result,
a certain amount of energy flows back and forth between
the two waveguide modes. From the view of supermode
theory, the oscillation is a result of beating between the
even and odd modes. Although the even mode is desired,
the coupling of the odd mode is not completely sup-
pressed, for example, if the length of the taper is not long
sufficiently according to the adiabatic criterion in [6].
When the odd mode propagates in the taper, there is cou-
pling between the even and odd modes and a small
amount of energy flows back and forth constantly. Since
at the end of taper, the majority of the energy of the even
mode is in As2S3 waveguide and that of the odd mode is
in Ti waveguide, there is a constant energy flow between
two waveguides, and consequently the coupling effi-
ciency oscillates.
In the presence of mode beating, it is not necessarily
the longer taper, the better coupling. There exists an op-
timum length for a taper with fixed width variation: if it
is shorter than that, the mode is under-coupled since it is
far away from the adiabatic criterion for 100% coupling;
if considerably longer than that, the coupling efficiency
is degraded by the resonant effect, as Figure 6 shows. In
order to reduce the problem of mode beating, we must
enlarge γ, either by increasing the phase mismatch δ or
by decreasing the coupling strength κ. δ is limited by the
property of the materials whereas κ can be controlled by
the structure. For example, κ can be reduced by intro-
ducing a gap between As2S3 waveguide and Ti wave-
guide.
Although the coupling efficiency can be as high as
96%, it takes quite a few millimeters to get a decent cou-
pling efficiency for linear tapers, which is not acceptable
for ultra-compact design. According to the above analy-
sis, efficient coupling takes place in the first part of taper
where As2S3 waveguide expands across the critical width
and correspondingly the phase mismatch δ changes from
a negative value to a positive one. That contributes to
efficient coupling and we want it to be sufficiently long.
Once most of energy has entered As2S3 waveguide, the
rest of the taper can be shortened. As a consequence, we
have arrived at a two-stage taper (Figure 3). Furthermore,
since the end width of the first stage (transition width)
can now be a much smaller value, the rate of width
change is reduced largely. Simulation shows that for the
first part of a two-stage taper, if the width varies from 1.0
μm to 1.6 μm (have some leeway for fabrication devia-
tions) in the length of 2 mm, the width increasing rate is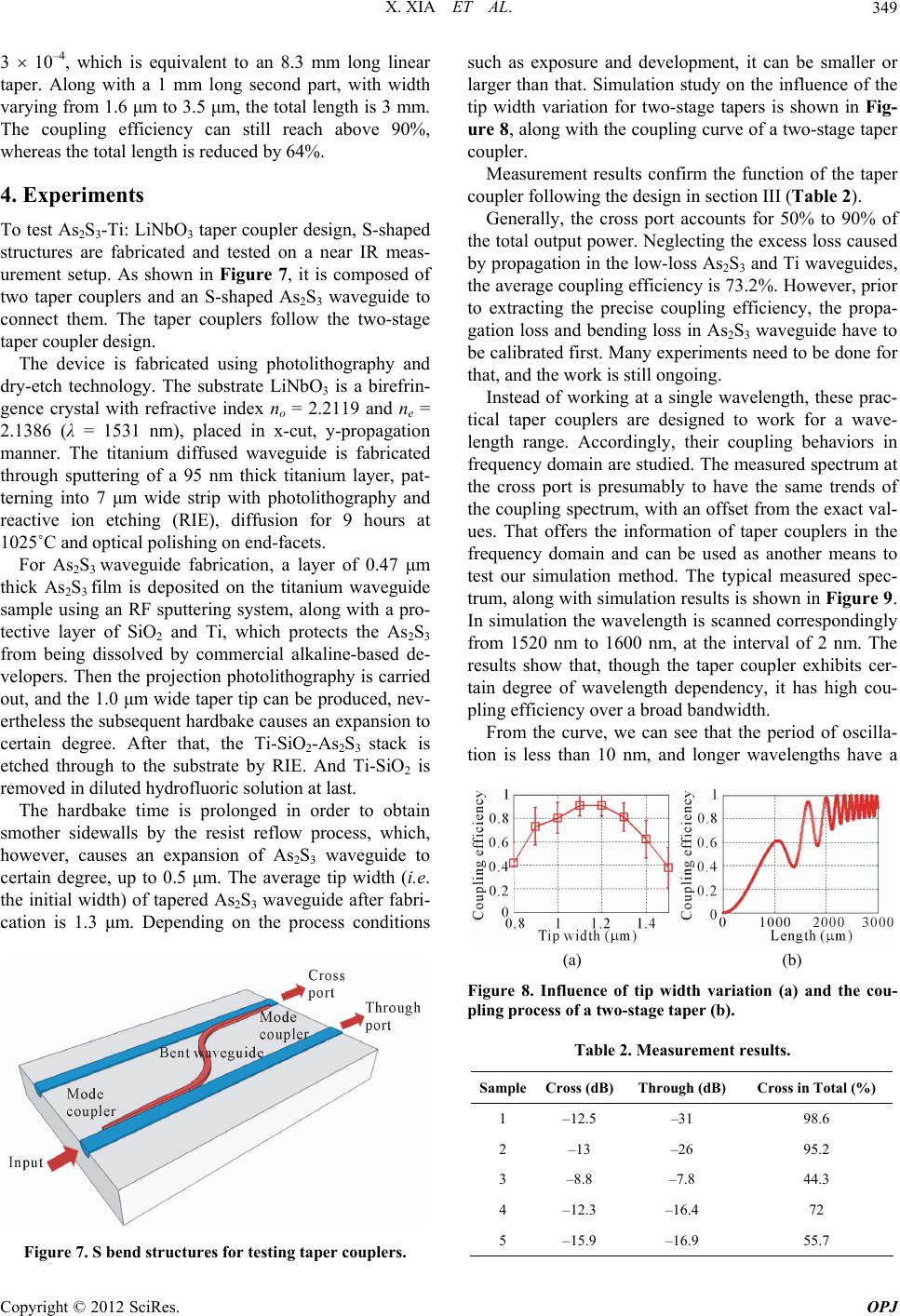

X. XIA ET AL. 349
3  10–4, which is equivalent to an 8.3 mm long linear
taper. Along with a 1 mm long second part, with width
varying from 1.6 μm to 3.5 μm, the total length is 3 mm.
The coupling efficiency can still reach above 90%,
whereas the total length is reduced by 64%.
4. Experiments
To test As2S3-Ti: LiNbO3 taper coupler design, S-shaped
structures are fabricated and tested on a near IR meas-
urement setup. As shown in Figure 7, it is composed of
two taper couplers and an S-shaped As2S3 waveguide to
connect them. The taper couplers follow the two-stage
taper coupler design.
The device is fabricated using photolithography and
dry-etch technology. The substrate LiNbO3 is a birefrin-
gence crystal with refractive index no = 2.2119 and ne =
2.1386 (λ = 1531 nm), placed in x-cut, y-propagation
manner. The titanium diffused waveguide is fabricated
through sputtering of a 95 nm thick titanium layer, pat-
terning into 7 μm wide strip with photolithography and
reactive ion etching (RIE), diffusion for 9 hours at
1025˚C and optical polishing on end-facets.
For As2S3 waveguide fabrication, a layer of 0.47 μm
thick As2S3 film is deposited on the titanium waveguide
sample using an RF sputtering system, along with a pro-
tective layer of SiO2 and Ti, which protects the As2S3
from being dissolved by commercial alkaline-based de-
velopers. Then the projection photolithography is carried
out, and the 1.0 μm wide taper tip can be produced, nev-
ertheless the subsequent hardbake causes an expansion to
certain degree. After that, the Ti-SiO2-As2S3 stack is
etched through to the substrate by RIE. And Ti-SiO2 is
removed in diluted hydrofluoric solution at last.
The hardbake time is prolonged in order to obtain
smother sidewalls by the resist reflow process, which,
however, causes an expansion of As2S3 waveguide to
certain degree, up to 0.5 μm. The average tip width (i.e.
the initial width) of tapered As2S3 waveguide after fabri-
cation is 1.3 μm. Depending on the process conditions
Figure 7. S bend structures for testing taper couplers.
such as exposure and development, it can be smaller or
larger than that. Simulation study on the influence of the
tip width variation for two-stage tapers is shown in Fig-
ure 8, along with the coupling curve of a two-stage taper
coupler.
Measurement results confirm the function of the taper
coupler following the design in section III (Table 2).
Generally, the cross port accounts for 50% to 90% of
the total output power. Neglecting the excess loss caused
by propagation in the low-loss As2S3 and Ti waveguides,
the average coupling efficiency is 73.2%. However, prior
to extracting the precise coupling efficiency, the propa-
gation loss and bending loss in As2S3 waveguide have to
be calibrated first. Many experiments need to be done for
that, and the work is still ongoing.
Instead of working at a single wavelength, these prac-
tical taper couplers are designed to work for a wave-
length range. Accordingly, their coupling behaviors in
frequency domain are studied. The measured spectrum at
the cross port is presumably to have the same trends of
the coupling spectrum, with an offset from the exact val-
ues. That offers the information of taper couplers in the
frequency domain and can be used as another means to
test our simulation method. The typical measured spec-
trum, along with simulation results is shown in Figure 9.
In simulation the wavelength is scanned correspondingly
from 1520 nm to 1600 nm, at the interval of 2 nm. The
results show that, though the taper coupler exhibits cer-
tain degree of wavelength dependency, it has high cou-
pling efficiency over a broad bandwidth.
From the curve, we can see that the period of oscilla-
tion is less than 10 nm, and longer wavelengths have a
(a) (b)
Figure 8. Influence of tip width variation (a) and the cou-
pling process of a two-stage taper (b).
Table 2. Measurement results.
Sample Cross (dB)Through (dB) Cross in Total (%)
1 –12.5 –31 98.6
2 –13 –26 95.2
3 –8.8 –7.8 44.3
4 –12.3 –16.4 72
5 –15.9 –16.9 55.7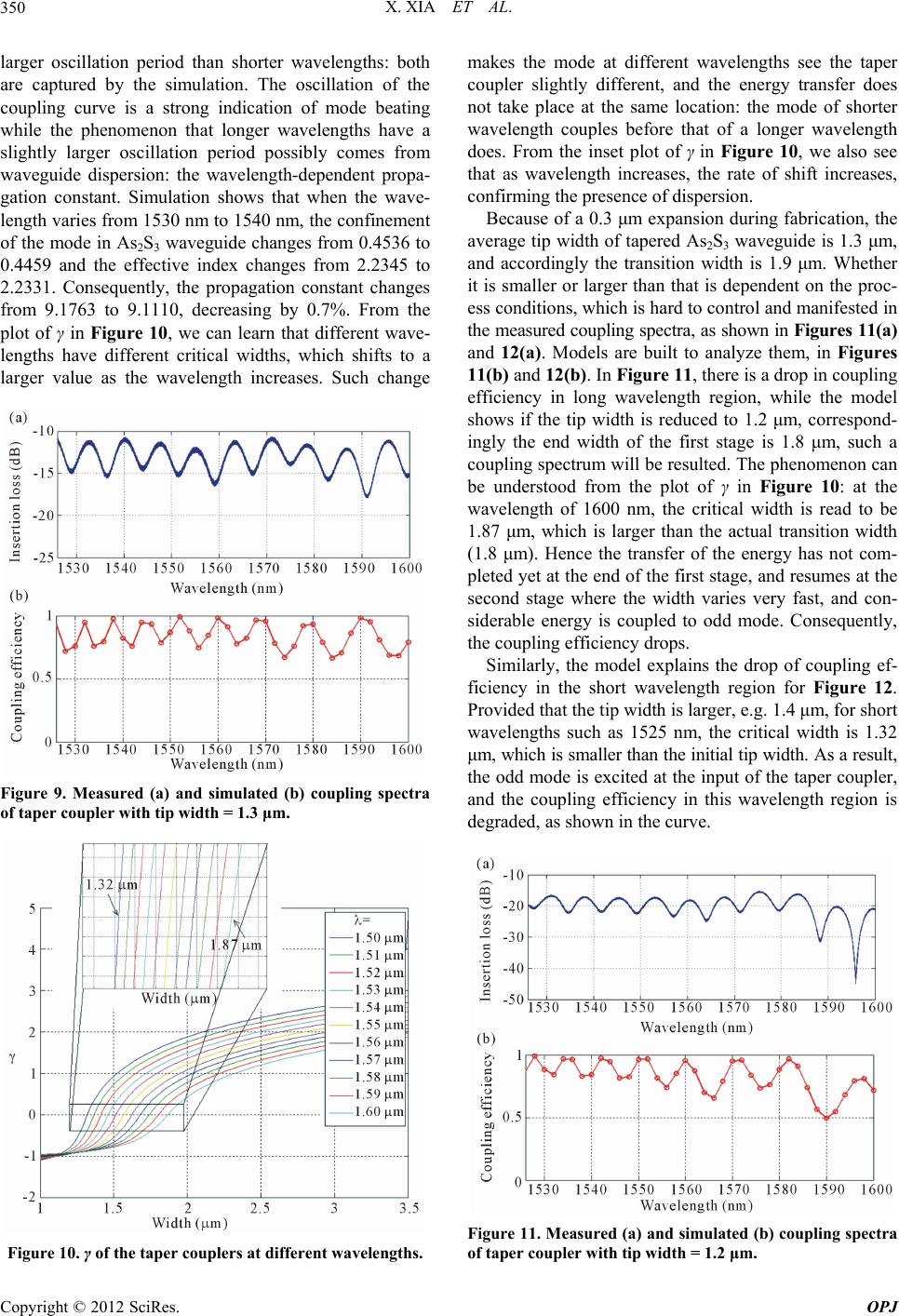

X. XIA ET AL. 350
larger oscillation period than shorter wavelengths: both
are captured by the simulation. The oscillation of the
coupling curve is a strong indication of mode beating
while the phenomenon that longer wavelengths have a
slightly larger oscillation period possibly comes from
waveguide dispersion: the wavelength-dependent propa-
gation constant. Simulation shows that when the wave-
length varies from 1530 nm to 1540 nm, the confinement
of the mode in As2S3 waveguide changes from 0.4536 to
0.4459 and the effective index changes from 2.2345 to
2.2331. Consequently, the propagation constant changes
from 9.1763 to 9.1110, decreasing by 0.7%. From the
plot of γ in Figure 10, we can learn that different wave-
lengths have different critical widths, which shifts to a
larger value as the wavelength increases. Such change
Figure 9. Measured (a) and simulated (b) coupling spectra
of taper coupler with tip width = 1.3 μm.
Figure 10. γ of the taper couplers at different wavelengths.
makes the mode at different wavelengths see the taper
coupler slightly different, and the energy transfer does
not take place at the same location: the mode of shorter
wavelength couples before that of a longer wavelength
does. From the inset plot of γ in Figure 10, we also see
that as wavelength increases, the rate of shift increases,
confirming the presence of dispersion.
Because of a 0.3 μm expansion during fabrication, the
average tip width of tapered As2S3 waveguide is 1.3 μm,
and accordingly the transition width is 1.9 μm. Whether
it is smaller or larger than that is dependent on the proc-
ess conditions, which is hard to control and manifested in
the measured coupling spectra, as shown in Figures 11(a)
and 12(a). Models are built to analyze them, in Figures
11(b) and 12(b). In Figure 11, there is a drop in coupling
efficiency in long wavelength region, while the model
shows if the tip width is reduced to 1.2 μm, correspond-
ingly the end width of the first stage is 1.8 μm, such a
coupling spectrum will be resulted. The phenomenon can
be understood from the plot of γ in Figure 10: at the
wavelength of 1600 nm, the critical width is read to be
1.87 μm, which is larger than the actual transition width
(1.8 μm). Hence the transfer of the energy has not com-
pleted yet at the end of the first stage, and resumes at the
second stage where the width varies very fast, and con-
siderable energy is coupled to odd mode. Consequently,
the coupling efficiency drops.
Similarly, the model explains the drop of coupling ef-
ficiency in the short wavelength region for Figure 12.
Provided that the tip width is larger, e.g. 1.4 μm, for short
wavelengths such as 1525 nm, the critical width is 1.32
μm, which is smaller than the initial tip width. As a result,
the odd mode is excited at the input of the taper coupler,
and the coupling efficiency in this wavelength region is
degraded, as shown in the curve.
Figure 11. Measured (a) and simulated (b) coupling spectra
of taper coupler with tip width = 1.2 μm.

X. XIA ET AL. 351
6. Acknowledgements
The authors would like to thank William Tim Snider and
Travis E. James for the help in fabrication. This publica-
tion was supported by the Pennsylvania State University
Materials Research Institute Nanofabrication Lab and
National Science Foundation Cooperative Agreement No.
0335765, National Nanotechnology Infrastructure Net-
work, with Cornell University.
REFERENCES
[1] M. E. Solmaz, et al., “Compact Bends for Achieving
Higher Integration Densities for LiNbO3 Waveguides,”
IEEE Photonics Technology Letters, Vol. 21, No. 9, 2009,
pp. 557-559. doi:10.1109/LPT.2009.2014569
[2] M. E. Solmaz, et al., “First Demonstration of an As2S3-
on-LiNbO3 Ring Resonator,” Conference on Optical Fi-
ber Communication—Incudes Post Deadline Papers, San
Diego, 22-26 March 2009, pp. 1-3.
Figure 12. Measured (a) and simulated (b) coupling spectra
of taper coupler with tip width = 1.4 μm.
[3] J. Haes, et al., “Design of Adiabatic Tapers for High-
Contrast Step Index Waveguides,” Linear and Nonlinear
Integrated Optics, Lindau, 11-13 April 1994, pp. 685-
693.
From the above analysis, we see a tradeoff between
the applicable wavelength range and the design parame-
ters, which, on the other side, provides a way of control-
ling the frequency domain behavior of taper couplers: by
adjusting the transition width between two stages we can
cut off longer wavelengths and by changing the tip width
we can suppress the coupling of shorter wavelengths.
[4] C.-T. Lee, et al., “Design and Analysis of Completely
Adiabatic Tapered Waveguides by Conformal Mapping,”
Journal of Lightwave Technology, Vol. 15, No. 2, 1997,
pp. 403-410.
[5] F. Xia, et al., “Photonic Integration Using Asymmetric
Twin-Waveguide (ATG) Technology: Part I-Concepts
and Theory,” IEEE Journal of Selected Topics in Quan-
tum Electronics, Vol. 11, No. 1, 2005, pp. 17-29.
doi:10.1109/JSTQE.2004.841466
5. Conclusion
A modeling method for taper couplers is developed and
applied to the study of As2S3-Ti: LiNbO3 taper couplers,
which are generally not adiabatic but highly efficient in
terms of practical use. Simulations show that for those
practical tapers, both adiabatic coupling and resonant
coupling play an important role. There exists an optimum
taper design with respect to the tip width, end width and
length. A two-stage taper design can largely reduce the
total length of the taper by 64% while keeping high cou-
pling efficiency above 90%. Following the guidelines,
test structures are fabricated. The measurement results
agree with the simulation results well, suggesting a good
coupling efficiency. Frequency domain analysis shows
that the taper couplers work for a range of wavelengths,
which can be controlled by adjusting the transition width
and the tip width.
[6] X. Sun, et al., “Adiabaticity Criterion and the Shortest
Adiabatic Mode Transformer in a Coupled-Waveguide
System,” Optics Letters, Vol. 34, No. 3, 2009, pp. 280-
282. doi:10.1364/OL.34.000280
[7] A. Yariv and X. Sun, “Supermode Si/III-V Hybrid Lasers,
Optical Amplifiers and Modulators: A Proposal and Analy-
sis,” Optics Express, Vol. 15, No. 15, 2007, pp. 9147-
9151. doi:10.1364/OE.15.009147
[8] J. Haes, et al., “A comparison between Different Propa-
gative Schemes for the Simulation of Tapered Step Index
Slab Waveguides,” Journal of Lightwave Technology,
Vol. 14, No. 6, 1996, pp. 1557-1569.
[9] J.-M. Liu, “Coupling of Waves and Modes,” In: J.-M. Liu,
Ed., Photonic Devices, Cambridge University Press, Cam-
bridge, 2005, p. 1052.