Journal of Modern Physics
Vol.06 No.11(2015), Article ID:60103,9 pages
10.4236/jmp.2015.611173
Reformulation of Relativistic Quantum Field Theory Using Region-Like Idealization of the Elementary Particle
Elsadig Naseraddeen Ahmed Mohamed
Founder and Director, Information Fluxes-FZE Company, Dubai, UAE
Email: s.naseraddeen@hotmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 July 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
The existence of any elementary particle in universe requires the existence of some region of universe occupied by it. By taking the volume of this occupied region, the author will reformulate the relativistic quantum field theory using new 3-dimensional region-like idealization of elementary particles and hereinafter will call the total volume of all regions occupied by the elementary constituent particles of the quantum system the occupied volume. Also the author will call the set of all regions of universe filled by elementary constituent particles of the quantum system the occupied path. Always any quantum system is existed at a head of its occupied path. This path is growing by mutual filling and leaving regions of universe by its elementary constituent particles. The conservation of this elementary constituent particle requires the conservation of its occupied volume during this process. This requirement could be summarized by the following conditions: 1) the total volume of all regions of universe filled by the elementary constituent particles of the quantum system minus the total volume of all regions of universe left by these elementary constituent particles must be equal to the occupied volume of the quantum system; 2) the total increase in the occupied volume of the quantum system due to the absorption of another elementary particles from outside its occupied regions minus the total decreasing in its occupied volume due to the emission of another elementary particles outside its occupied regions must be equal to the occupied volume of it. The wave-particle duality of the elementary constituent particles implied accumulation of them as the finite set of interfered waves. This accumulation of elementary constituent particles causes the absolute probabilistic nature of event of finding the elementary consistent particle in specified interfered wave, and hence the mathematical representation of this interfered wave should take into account the value of probability amplitude of finding an elementary particle inside the region occupied specified interfered wave. In quantum theory this probability amplitude corresponds to complex amplitude of the wave function of interfered wave. Also in Hilbert’s representation of the quantum theory these wave functions are representing the components of the quantum state vector. In this paper the author will develop the transformation theory of the region-like quantum state of the quantum system.
Keywords:
Region-Like Idealization, Creation, Annihilation, Animation, Occupied Volume, Occupied Path, Relativistic Quantum Field Theory

1. Basic Definition and Equations
1.1. The Occupied Volume of the Elementary Particle
The occupied volume of the elementary particle is the measurement of the volume of the region of universe occupied by it.
1.2. The Occupied Volume of the Quantum System
The occupied volume of the quantum system is the total occupied volume of its elementary constituent particles.
1.3. Defining the Occupied Volume of the Quantum System as Linear Combination of Its Elementary Constituent Particles
If we have a quantum system consist of N interference pattern then the occupied volume of the quantum systems is always given as following linear combination.
 (1.1)
(1.1)
where
 and
and
 is the set of all bosons in universe with distinct occupied volumes and
is the set of all bosons in universe with distinct occupied volumes and
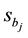 is the occupied volume of the boson
is the occupied volume of the boson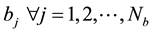 .
.
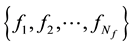 is the set all fermions in universe with distinct occupied volumes and
is the set all fermions in universe with distinct occupied volumes and
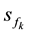 is the occupied volume of the fermion
is the occupied volume of the fermion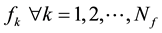 ,
,
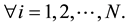
 is the number of the bosons identical to
is the number of the bosons identical to
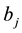 belonging to the ith interfered wave of the quantum system
belonging to the ith interfered wave of the quantum system .
.
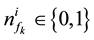 is the number of the fermions identical to
is the number of the fermions identical to
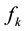 belonging to the ith interfered wave of the quantum system
belonging to the ith interfered wave of the quantum system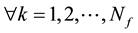 . This number must fulfill the Pauli’s exclusion principle [1] .
. This number must fulfill the Pauli’s exclusion principle [1] .
1.4. Defining the Occupied Volume of the Elementary Particles as Function of Its Wavelength
Up to now the shape of all elementary particles does not approved; so suppose that in general form the occupied volume of elementary particle is representing function of its wavelength
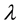 given as following:
given as following:


For example if the shape of boson


So the wavelength of the boson





By the same way if the shape of fermion fk is sphere then the occupied volume of fermion fk in this case is:

Also the inverse of




1.5. Defining the Speed of the Elementary Particle as Function of Its Occupied Volume
From the De-Broglie’s wave-particle duality the momentum of the elementary particle p is related to its wavelength




And hence by combination of De-Broglie’s formula


®
®
®
®
®

However


And hence






where



Important Notes










Those two equations imply that the exchange of elementary particles between the quantum systems is bounded by speed of light c, and hence there is no action at distance on any quantum system in universe.
1.6. Defining the Mass of the Elementary Particle as Function of Its Occupied Volume




From the theory of special relativity the mass of the elementary matter particle m is representing function of its wavelength


®

®

1.7. Defining the Total Relativistic Energy of the Elementary Particle as Function of Its Occupied Volume
From the theory of special relativity the relativistic total energy E of the elementary matter particle is represent- ing function of its wavelength


®

®

1.8. The Region-Like Quantum State of the Quantum System
In the quantum mechanics the classical Newtonian equation of motion is replaced by another called Schrodinger’s equation. However the solution of Schrödinger equation is a wave function which is complex function of spatial and temporal coordinates with complex amplitude equal to probability of finding elementary particle at specified spatial and temporal coordinates, although the spatial coordinates is related to point-like idealization of elementary particle the temporal coordinate is not, so in region-like idealization of this waves we need to replace all spatial parameters of the wave function by occupied volumes of elementary constituent particles, so if we have quantum system consist of N interfered wave then the region-like quantum state of this quantum system at each instance of time t is representing the following ket vector:

where

Important Notes
1) The ith component of


2) The time derivation of


3)


1.9. The Process of Creating of the Quantum System
The process of creating of the quantum system is the process in which the quantum system undergoes increasing in its occupied volume due to the absorption of elementary particles from outside its occupied region.
1.10. The Process of Annihilating of the Quantum System
The process of annihilating of the quantum system is the process in which the quantum system undergoes decreasing in its occupied volume due to the emission of elementary particles outside its occupied region.
1.11. The Process of Animating of the Quantum System
The process of animating of the quantum system is the process in which the quantum system mutually fills and leaves region of universe.
1.12. The Occupied Path of the Quantum System
The occupied path of the quantum system is the 3-dimentional path followed by it during its creating, annihilating and animating process and consists of all regions of universe occupied by its elementary constituent particles.
1.13. The Creating and Annihilating Interaction between the Quantum Systems
The creating and annihilating interaction between the quantum systems is the creating and annihilating process of two or more quantum systems in which the total occupied volume of one quantum system changed due to transformation of elementary particles from or to another quantum system.
1.14. The Unified Creating, Annihilating and Animating Law of Quantum Systems
Now we could define the unified creating and animating law that govern the behavior of quantum system during its creating, annihilating and animating processes as following:
The transformation of the occupied volume of the quantum system form initial value


where:








And hence


to the final state:
is always governing by the following equations:

where







Such that

1)



2)



3)


















Important Notes
1) The Equation (1.19) implied the equivalent between the deference i − d―where i is a dynamical variable of the process of creating and d is the dynamical variable of the process of annihilating―and the deference o ? l― where o and l are the dynamical variables of process of animating―so this equation implied the equivalent between the dynamical variables of creating, annihilating and animating processes.
2) Although the dynamical variables of the creating and annihilating process i, d could counted by the particle counters installed outside the region occupied by the elementary constituent particles of the quantum system, the animating dynamical variables immeasurable by this way, however the Equation (1.20) implied the complete equivalents between the dynamical variable of creating, annihilating and animating process and hence for each measurable dynamical variables of the process of creating and annihilating there exist an equivalent dynamical variables of animating satisfy the Equations (1.20) and (1.21).
2. The Transformation Theory of the Region-Like Quantum State
2.1. The Outer Product (Tensor Product)


Important Notes
1) The outer product


2)
2.2. Theorem 2-1
If




Prove:
2.3. The Time Evolution Equation of the Region-Like Quantum State of the Quantum System during the Processes of Creating, Annihilating and Animating
From the Theorem 2.1:

and

And hence from the Equation (1.21) the time evolution of the region-like quantum state of the system is given by the following equations:



Important Note
1)


2) We could calculate the components of


(2.5) tell us the equivalents between the components of


3)



3. Figures
1) In Figure 1, the part of occupied path of the red hand of speedometer start at 80 point and then the red hand continue to mutually occupy and leave regions between two points 80 and 100 until arrived near 100 point.
2) In Figure 2, the mutual occupying and leaving of universe’s regions by the boson



Figure 1. Example of occupied path (the occupied path of hand of vehicle speedometer).
Figure 2. The left imaginary sphere is representing the region left by boson bj and right imaginary sphere represent the occupied region by boson bj when it completely left the left spherical region.
4. Conclusion
Using region-like idealization of the elementary constituent particles of the quantum system we could introduce a new formulation of the quantum theory independent from the energy scale, and hence free from hierarchal problem.
Acknowledgements
Thanks for my father who supported all of my educational levels and for my wife Ayaat Ahmed Osman for here incorporeal support to me on publication of this paper.
Cite this paper
Elsadig Naseraddeen AhmedMohamed, (2015) Reformulation of Relativistic Quantum Field Theory Using Region-Like Idealization of the Elementary Particle. Journal of Modern Physics,06,1711-1720. doi: 10.4236/jmp.2015.611173
References
- 1. Wolfgang Pauli’s Nobel Lecture Titled by “Exclusion Principle and Quantum Mechanics”.
http://www.nobelprize.org/nobel_prizes/physics/laureates/1945/pauli-lecture.pdf - 2. The De-Broglie’s Nobel Lecture.
http://www.nobelprize.org/nobel_prizes/physics/laureates/1929/broglie-lecture.pdf - 3. van der Waerden, B.L. From Matrix Mechanics and Wave Mechanics to Unified Quantum Mechanics.
http://www.ams.org/notices/199703/vanderwaerden.pdf - 4. Lipcshutz, S. and Lipson, M. (2009) Linear Algebra. 4th Edition, Schaum’s Outlines, McGraw Hill, USA.
























