Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21668,9 pages DOI:10.4236/jmp.2012.38112
Three-Photon Absorption in ZnO Film Using Ultra Short Pulse Laser
Department of Physics, College of Science, University of Baghdad, Baghdad, Iraq
Email: raiedkamel@yahoo.com, Abdulla_shl@yahoo.com, mohammedtaki97@yahoo.com, hani_saka@yahoo.com
Received January 4, 2012; revised February 1, 2012; accepted February 27, 2012
Keywords: Multiphoton Processes; ZnO Nanocrystalline; Nonlinear Optics
ABSTRACT
The three-photon absorption (3PA) in nanostructure wide-band gap ZnO semiconductor material is observed under high intensity femtosecond Titanium-Sapphire laser of 800 nm wavelength excitation. The ZnO film was prepared by chemical spray pyrolysis technique with substrate temperature of 400˚C. The optical properties concerning the absorption, transmission, reflection, Raman and the photoluminescence spectra are studied for the prepared film. The structure of the ZnO film was tested with the X-ray diffraction and it was found to be a polycrystalline with recognized peaks oriented in (002), and (102). The measured of three photon absorption coefficient was found to be about 0.0166 cm3/Gwatt2, which is about five times higher than the bulk value. The fully computerized z-scan system was used to measure the nonlinear coefficients from the Gaussian fit of the transmitted laser incident.
1. Introduction
The ZnO nanostructures have many applications in gas sensors, UV detectors and solar cells [1-3]. This material has some additional advantages compared to other large band-gap semiconductors; for example, its large exciton binding energy (about 60 meV) which is three times the binding energies of ZnSe and GaN [4]. This allows a stable exciton distribution and achieves efficient excitonic emission at room temperature. The optical and electrical properties of ZnO nanostructures are studied at different preparation techniques and at different substrate materials [5,6]. The pumping of ZnO crystalline nanofilm with near-infrared femtosecond radiation pulses, enhances the nonlinear interaction between the ultrahigh intensity applied optical field and the ZnO nanostructures [7,8]. The nonlinear interaction leads to the simultaneous absorption of two or more photons of subband gap energy. The absorption is through a virtual-states that assists the inter band transitions. This transition produces electron-hole pairs in the excited states and, subsequently, the band-edge emission via their radiative recombination [9]. The two photon absorption (2PA) in semiconductor nanocrystals (NCs) has been widely investigated [8,10], while the research effort on their three-photon absorption (3PA) is limited [11]. The three photon absorption was observed in ZnO and ZnS crystals when pump with lasers of ultra excitation irradiance which was more than 40 GW/cm2 [12-15]. Three-photon absorption in nanostructure wide-Band gap semiconductor ZnO using femtosecond laser for thin film was studied by [16].
In this work the three photon absorption in ZnO nanostructure illuminated by intensity 110 GW/cm2 Ti-Sapphire laser is observed. The work concentrates on the effect of the nanostructure on the nonlinear parameters through the studying of the 3PA coefficient and the laser threshold pumping power. Simple mathematical relations are developed to describe the dependence of the fluorescent emission on the pumping laser intensity. The three photon absorption coefficient was calculated from the experimental measurements.
2. Experimental Work
The ZnO film was prepared by chemical spray pyrolysis technique. The film was deposited on quartz substrates heated to 400˚C. The spray solution is prepared by mixing Zinc Chloride (ZnCl2) at 0.1 M with distillated water. The above mixture solution was placed in the flask of the atomizer and spread by controlled nitrogen gas flow on the heated substrates. The chemical spray pyrolysis experimental setup is similar to the standard unit fully described by [17]. The spraying time was controlled by adjustable a solenoid valve. The heated substrate was left for 12 sec after each spraying run to give time for the deposited ZnO layer to be dry. In order to get film of proper thickness many layers deposited of ZnO are required. The optimum experimental conditions for obtaining homogeneous ZnO film at 400˚C are determined by the spraying time, the drying time and the flashing gas pressure. The schematic representation of the spray system is given in Figure 1. The possible reaction of the spray chemical on the heated substrate is yielding for the following reaction:
ZnCl2 + H2O  ZnO (film/substrate) + 2HCl (1)
ZnO (film/substrate) + 2HCl (1)
During the chemical reaction, gas and water vapor is obtained from this reaction due to the high temperature of the substrate. At end of reaction a white precipitates remain from the reaction as a nanofilm of ZnO as shown in Figure 2. The topography study of the prepared nanofilm surface was carried on using Scanning Electron Microscopy (SEM) type ULTRA 55 with different magnification; as shown in Figure 3. The X-ray diffraction (XRD) pattern of ZnO film was recorded by XDR 2000. The X-ray diffractometer use copper tube radiation line of wavelength 1.54Å in 2θ range from 20˚ to 60˚. The scanning rate was 1 deg/min.
The UV-VIS-NIR absorption, transmission and reflection spectra of the sample were recorded by Hitachi U-4100 spectrometer covering the spectral range 200 - 1100 nm. The photoluminescence spectrum (PL) was studied using SL1174 spectrophotometer in the range 300 - 900 nm.

Figure 1. Schematic representation of the spray system.

Figure 2. A photo of spray pyrolyzed ZnO nanofilm on glass samples.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f)
Figure 3. (a)-(e) represent SEM images of ZnO nanofilm at different magnification power and (f) for a sample thickness.
The nonlinear absorption study at the near resonant regime was carried out using single beam femtosecond z-scan technique. The z-scan setting is illustrated by schematic diagram shown in Figure 4. A femtosecond laser of pulse duration 60 fs and of average power 0.165 W was used as a laser source. The pulse duration was measured by autocorrelation system and the energy was measured by pyroelectric energy prob model type (PDA36A), covering the rang 350 - 1100 nm from THORLABS. The beam profile was adjusted by spatial filter leading to spatial intensity profile near Gaussian with beam quality of M2 ≈ 1.79. The laser beam was focused by a lens of 15 cm focal length to produce a waist of 22.5 µm. The sample was translated along the beam axis (z-axis) through the Rayleigh distance 2000 µm. The distance from lens to aperture was 53 cm and beam diameter at detector was 16.4 mm.
3. Results and Discussion
The topography study of the prepared film shows the formation of the ZnO nanostructure and the film thickness was around 2 µm. as reveled by Scanning Electron Microscopy (SEM) type ULTRA 55 with different magnification; as shown in Figure 3. These figures showed nanocrystals of size ~(100 - 200 nm). The sample was scanned in all zones before the picture was taken. The micrographs reveled that the particles were hexagonal in shape. This indicated that ZnO nanocrystal were grown with c-axis orientation and almost perpendicular to the substrate surface as observed in the scanning electron microscope (SEM) image.
The XRD pattern of ZnO film prepared with 2 µm thickness is illustrated in Figure 3. The spectrum indicates that the ZnO film is a polycrystalline structure. The observed values of the XRD peaks are compared with American Society for testing and Material (ASTM) data for hexagonal zinc oxide. It can be noticed from the XRD pattern the strongest peak observed at Bragg’s angle 2θ = 34.38˚ can be attributed to the (002) plan of the hexagonal ZnO and the interplanar distance can be determined by Bragg’s law, d002 = 0.26 nm. The (102) peak is also observed at 2θ = 47.44˚ but this peak is much lower intensity than the (002) peak. The figure shows broad peaks which give evidence of the nanostructure formation. Using the width of (002) peak which appears at angle 34.38˚ on 2θ scale in Scherrer’s formula [18]:
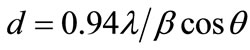 (2)
(2)
where d is the average crystalline grain size, λ is the wavelength, β represents the full width at half maximum (FWHM) in radian and θ is the Bragg diffraction angle in degree. The size of the formed nanoparticles was found to be about 46 nm, this value is close from the value that measured by SEM. Using the width of (102) peak which appears at angle 47.44˚ on 2θ scale the size of the formed nanoparticles was found to be about 26 nm. The interplaner distance can be determined by Bragg’s law d102 = 0.19 nm.

Figure 4. Schematic of the z-scan setup recording the nonlinear absorption, R-rotator, P-polarizer, SF-spatial filter, BS1, BS2-beam splitter, Au-autocorrelation, D1,D2-detectors, L-lens, S-sample.
The optical properties of ZnO film which were prepared on quartz substrate have been studied in this work. The absorption spectrum of the ZnO film is shown in Figure 5. This spectrum shows low absorption in the visible and infrared regions; however, the absorption in the ultraviolet region is high. This result were in agreement with the absorption spectrum which obtained by other workers. The energy band gap of ZnO film was estimated using Tauc equation which can be written as:
 (3)
(3)
where A is a constant, α absorption coefficient, hν the photon energy (Eg) the band gap, n =  for the direct transitions. Referring to the data extracted from the absorption spectrum in Figure 6, the absorption coefficient (α) was calculated as a function of wavelength. Assuming allowed transition; the dependence of (αhν)2 on (hν) is plotted as in Figure 7. The extrapolation of the linear part of the plot (αhν)2 = 0, gives rise on estimation of the energy gap value of the prepared ZnO film. The value of the energy gap was found to be about 3.3 eV. This value was in a good agreement with values mentioned by other works.
for the direct transitions. Referring to the data extracted from the absorption spectrum in Figure 6, the absorption coefficient (α) was calculated as a function of wavelength. Assuming allowed transition; the dependence of (αhν)2 on (hν) is plotted as in Figure 7. The extrapolation of the linear part of the plot (αhν)2 = 0, gives rise on estimation of the energy gap value of the prepared ZnO film. The value of the energy gap was found to be about 3.3 eV. This value was in a good agreement with values mentioned by other works.

Figure 5. UV-VIS absorption spectra of ZnO nanofilm.
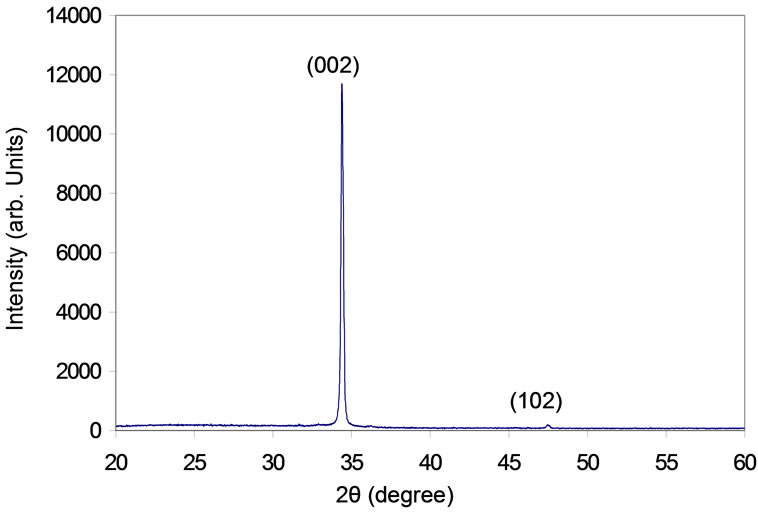
Figure 6. XRD pattern of ZnO nanofilm deposited on a glass substrate at 400˚C.
The optical transmittance spectrum of the ZnO film is shown in Figure 8. It can be noticed from this figure that the transmittance is high in the visible and infrared regions and low transmission in ultraviolet region.
The optical reflection spectrum of the ZnO film is shown in Figure 9. It can be noticed from this figure that the maximum reflection at 470 nm and minimum value was 390 nm. The optical fluorescence spectrum of the

Figure 7. Plot of (ahv)2 versus photon energy hv for ZnO nanonanofilm.

Figure 8. Optical transmission spectra of ZnO nanofilm.
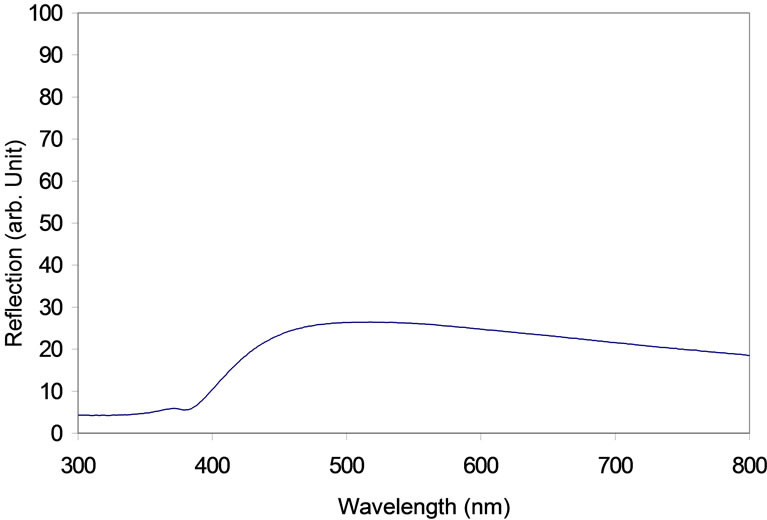
Figure 9. Optical reflection spectra of ZnO nanofilm.
ZnO film illuminated by 320 nm UV line is shown in Figure 10. The spectrum displays two major luminance peaks at 380 nm and around 556 nm. The first peak is due to the energy gap transmission which corresponds to 3.28 eV. The second peak is due to the excitonic emission; and it is in a good agreement with the results measured by many other authors [19,20]. The broad green emission peak that is dominated at 556 nm (≈2.23 eV) is a good evidence for the exciton formation in ZnO with a binding energy of 60 meV. The high binding energy enables the finding of the exciton at room temperature. The intensity at the 556 nm peak is higher than that found around 380 nm peak. This is because the band-to-band transition was quenched by the defect states. The same behavior was observed by [21].
The Raman active zone-center optical phonons predicated by the group theory are A1 + 2E2 + E1. The phonons of A1 and E1 symmetry are polar phonons and, hence, exhibit different frequencies for the transverseoptical (TO) and longitudinal optical (LO) phonons. In wurtzite ZnO crystals, The non-polar phonon modes with symmetry E2 have two frequencies, E2(high) is associated with oxygen atoms and E2(low) is associated with Zn sublattice. The described phonon modes have been reported in the Raman scattering spectra of bulk ZnO [22,23]. In Figure 11, we present a typical non-resonant Raman scattering spectrum from ZnO nanocrystal obtain under the 633 nm non-resonant excitation on of He-Ne laser. For comparison, the phonons peaks observed in bulk ZnO crystal are summarized in Table 1.
In our experiment, Raman spectra were recorded at room temperature under the 633 nm excitation and laser power 75 mW, the E2(low) peak is red shifted by ~3 cm–1 from its bulk value, E2(high) peak is red shift by ~2 cm–1, but the peak E1(LO) at 591 cm–1 corresponding to E1(LO). The A1(TO), E1(TO), A1(LO) peaks being absent in this sample.
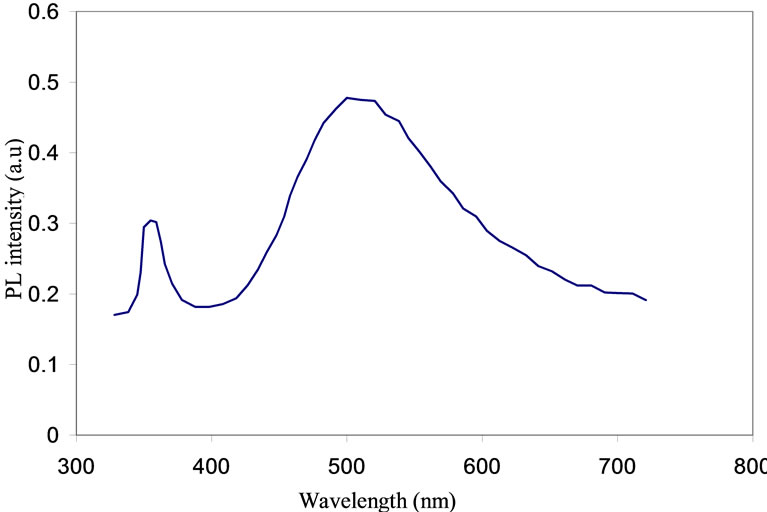
Figure 10. Photoluminescence emission spectrum of ZnO nanofilm.
There are three possible mechanisms for the phonon peak shift in Raman spectra of nanostructures. The first one is spatial confinement within the quantum dot (nanocrystal) boundaries. The second one is related to the phonon localization by defect. Nanocrystal or quantum dots, produced by chemical methods or by the molecularbeam epitaxy, normally have more defect than corresponding bulk crystal. In order elucidate the possible of the peak shifts we carried out simple calculations in the framework of the H. Richer [24] and I. H. Chambell [25] phenomenological models.
The z-scan transition curve at 110 GW/cm2 excitation intensity is recorded for the nanoparticles ZnO film and it shown in Figure 12, Where the average power was 0.165 W, Repetition rate (RR) was 250 kHz, Pulse energy Ep was 6.6 × 10–7 J, Pulse duration (FWHM) was 60 fs, Peak power (PP) was 10.34 × 106 W.

Figure 11. Non-resonant Raman spectra from ZnO nanocrystal under 633 nm excitation and 75 mW for He-Ne laser.

Table 1. Raman active phonon mode frequencies (in cm–1) for bulk ZnO.
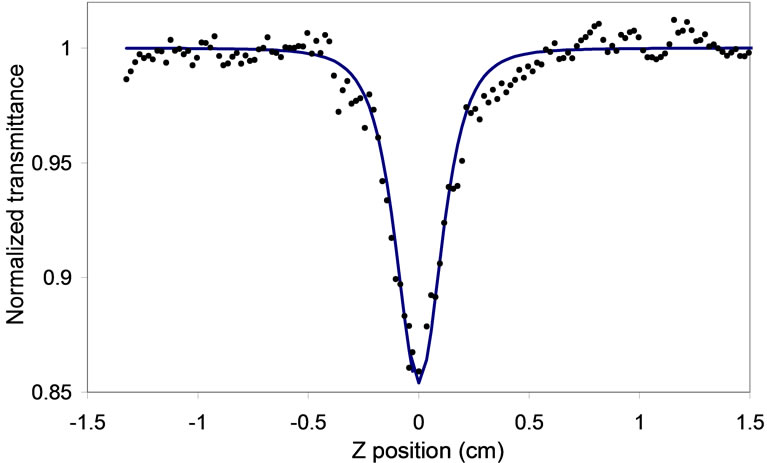
Figure 12. OA Z-scan measured at irradiance 110 GW/cm2, wavelength 800 nm, a pulse duration 60 fs and repetition rate of 250 kHz. The solid line is the fitting curve employing the z-scan theory, described in the text, on 3PA.
The rate equations model describing the transitions between the valance band and the conduction band in our semiconductor sample illuminated by Titanium-Sapphire femtosecond laser of 800 nm wavelength can be written as:
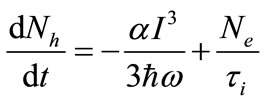 (4)
(4)
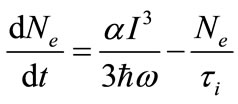 (5)
(5)
where Nh and Ne are the population in the valance band and the conduction band respectively. α is the three photon absorption coefficient, ћω is the energy of the IR pump Titanium-Sapphire laser photon, I is the laser intensity at the sample position and τi is the life time of the excited level in the conduction band. The Gaussian laser beam intensity is given by:
 (6)
(6)
where Io is the laser intensity at the waist of the beam and 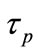 is the laser pulse duration. Since the measuring intensity was carried out at the focal point, in the Z-coordinate, thus the intensity in Equation (4) can be reduced to I = Io. In order to find the relation between the power of the out put emitted fluorescent pulse and the intensity of the Titanium-Sapphire laser pump, Equation (5) can be arranged as:
is the laser pulse duration. Since the measuring intensity was carried out at the focal point, in the Z-coordinate, thus the intensity in Equation (4) can be reduced to I = Io. In order to find the relation between the power of the out put emitted fluorescent pulse and the intensity of the Titanium-Sapphire laser pump, Equation (5) can be arranged as:
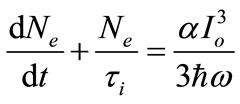 (7)
(7)
The solution of Equation (7) can be written as:
 (8)
(8)
Since the pulse duration of the pump laser (τp) is in femtosecond and the life time of the excited state (τi) in picosecond [26], the Equation (8) can be simplified as:
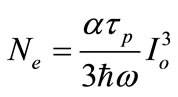 (9)
(9)
Multiply both sides of the above equation by the volume (V) of the illuminated part of the ZnO sample and arranged the terms, Equation (9) can be written as:
 (10)
(10)
where Pf is the power of the emitted fluorescent from the ZnO sample pumped by the Titanium-Sapphire laser. Introducing the quantum yield which include the probability of the exciton self-trapping and the efficiency of the detection unit, Equation (10) can be written as:
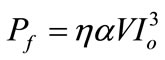 (11)
(11)
In our experimental setting described before, the focal spot are about 1590 µm2 and the ZnO film has 2 µm thickness, thus the illuminated volume is about 3180 µm3 and η was estimated to by 10–5 in our experimental set up. The value of (a) is found from the measurements of Pf at different values of Io, and by applying Equation (11), it was found to by about of 0.0142 cm3/GWatt2. The result which is not far away from the calculate result from Gaussian fit technique as follow:
The normalized energy transmittance for 3PA of the open aperture z-scan is given by R. L. Sutherland [27]:
 (12)
(12)
where 
 is the excitation intensity at the position z,
is the excitation intensity at the position z,  where zo is the Rayleigh range, ωo is the minimum beam waist at focal point (z = 0), λ is the laser free-space wavelength,
where zo is the Rayleigh range, ωo is the minimum beam waist at focal point (z = 0), λ is the laser free-space wavelength,
 is the effective sample length for 3PA processes; L is the sample length and ao is the linear absorption coefficient. The open aperture z-scan graph is always normalized to linear transmittance i.e., transmittance at large values of |z|. If Po < 1 Equation (12) can be expanded in a Taylor series as:
is the effective sample length for 3PA processes; L is the sample length and ao is the linear absorption coefficient. The open aperture z-scan graph is always normalized to linear transmittance i.e., transmittance at large values of |z|. If Po < 1 Equation (12) can be expanded in a Taylor series as:
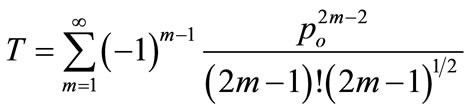 (13)
(13)
Furthermore, if the higher order terms are ignored, the transmission as a function of the incident intensity is given by R. L. Sutherland [27]:
 (14)
(14)
The 3PA coefficient can be extracted from the best fit for Equation (14). The sold curve in Figure 12 is the best fit for Equation (14). The Equation (14) shows clearly that the depth of the absorption dip is linearly proportional to the 3PA coefficient γ, but the shape of the trace is primarily determined by the Rayleigh range of the focused Gaussian beam. The fitted value of γ is on the order of 0.0166 cm3/Gwatt2. This value is five times of magnitudes higher than the value observed with bulk ZnO sample. The natural logarithm of the (1 − T) values are plotted as a function of natural logarithm of the incident intensity Io in Figure 13. the curve can be reasonably fitted with a straight line with slope of 1.99, this indicate that the 3PA was occur in ZnO pump by 800 nm laser source of 60 fs pulse duration.
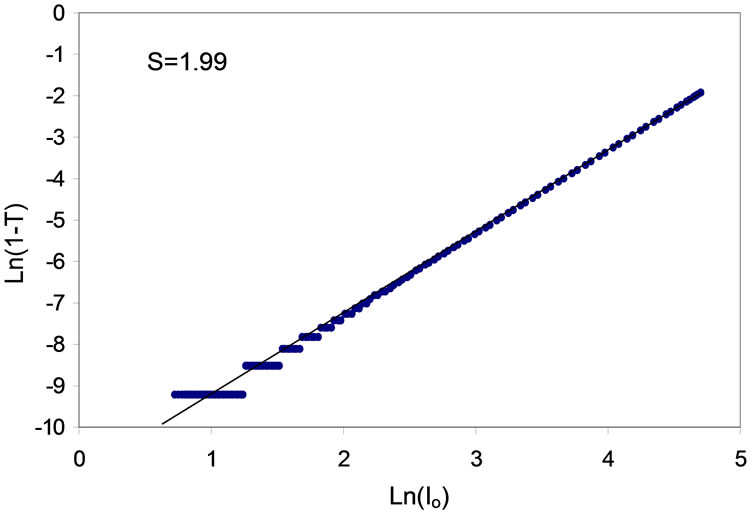
Figure 13. Plot of Ln(1 − T) versus Ln(Io) at 800 nm wavelength, the solid line is the example of the linear at 800 nm with slope s = 1.99.
4. Conclusion
The three photon absorption has been observed in ZnO nanocrystalline prepared by chemical method upon illuminating it by femtosecond Titanium-Sapphire laser. The fully computerized z-scan system was used to measure the nonlinear absorption coefficient of the prepared samples. The value of the measured nonlinear coefficient was found to be five times higher than the bulk value. The enhancement of the nonlinear coefficient was attributed to the formation of the nanocrystallites of ZnO and to the existence of the exciton in the prepared film.
5. Acknowledgements
This work has been carried out in the physics Department, School of Engineering and Applied Sciences, Harvard University. The authors would like to thanks Mazur Research Group in Harvard University for their help through this work. Thank also to Christopher C. Evans, Jonthan D. B. Bradley, and Eric Mazur for their interest, guide and useful discussion. We thanks also the Ministry of Higher Education in the republic of Iraq for support this work.
REFERENCES
- Y. w. Zhu, et al., “Multiwalled Carbon Nanotubes Beaded with ZnO nanoparticles for Ultrafast Nonlinear Optical Switching,” Advanced Materials, Vol. 18, No. 5, 2006, pp. 587-592. doi:10.1002/adma.200501918
- K. Ramanathan, J. Keane and R. Noufi, “Properties of High-Efficiency CIGS Thin-Film Solar Cells,” NREL/CP, Vol. 520, 2005, Article ID: 37404.
- C. L. Rhodes, S. Lappi, D. Fischer, S. Sambasivan, J. Genzer and S. Franzen, “Characterization of Monolayer Formation on Aluminum-Doped ZincOxide Thin Films,” American Chemical Society, Vol. 24, No. 2, 2008, pp. 433-440.
- H. Li, et al., “Microstructural Study of MBE-Grown ZnO Film on GaN/Sapphire (0001) Substrate,” Central European Journal of Physics, Vol. 6, No. 3, 2008, pp. 638-642. doi:10.2478/s11534-008-0032-2
- T. Sato, et al., “Production of Transition Metal-Doped ZnO Nanoparticles by Using RF Plasma Field,” Journal of Crystal Growth, Vol. 275, No. 1-2, 2005, pp. 983-987. doi:10.1016/j.jcrysgro.2004.11.152
- S. Singh and M. S. R. Rao, “Structure and Physical Properties of Undoped ZnO and Vanadium Doped ZnO Films Deposited by Pulsed Laser Deposition,” Journal Nanoscience and Nanotechnology, Vol. 8, No. 5, 2007, pp. 2575-2577.
- Ü. Özgür, et al., “A Comprehensive Review of ZnO Materials and Devices,” Journal of Applied Physics, Vol. 98, No. 4, 2005, Article ID: 041301. doi:10.1063/1.1992666
- J.-H. Lin, et al., “Two-Photon Resonance Assisted Huge Nonlinear Refraction and Absorption in ZnO Thin Films Institute of Electro-Optical Engineering,” Journal of Applied Physics, Vol. 97, No. 3, 2005, Article ID: 033526. doi:10.1063/1.1848192
- S. J. Bentley, et al., “Three-Photon Absorption for Nanosecond Excitation in Cadmium Selenide Quantum Dots,” Optical Engineering, Vol. 46, No. 12, 2007, Article ID: 128003. doi:10.1117/1.2823156
- E. W. Van Stryiand, M. Sheik-Bahae, A. A. Said and D. J. Hagan, “Characterization of Nonlinear Optical Absorption and Refraction,” Progress in Crystal Growth and Characterization of Materials, Vol. 27, No. 3-4, 1993, pp. 279-311. doi:10.1016/0960-8974(93)90026-Z
- J. He, W. Ji and J. Mi, “Three-Photon Absorption in Water-Soluble ZnS Nanocrystal,” Applied Physics Letters, Vol. 88, No. 18, 2006, Article ID: 181114. doi:10.1063/1.2198823
- B. Gu, et al., “Three-Photon Absorption Saturation in ZnO and ZnS Crystals,” Journal of Applied Physics, Vol. 103, No. 7, 2008, Article ID: 073105. doi:10.1063/1.2903576
- S. Pearl, et al., “Three Photon Absorption in Silicon for 2300 - 3300 nm,” Applied Physics Letters, Vol. 93, No. 13, 2008, Article ID: 131102. doi:10.1063/1.2991446
- A. Penzkofer and W. Falkenstein, “Three Photon Absorption and Subsequent Excited-State Absorption in CdS,” Optics Communications, Vol. 16, 1976, pp. 247-250.
- M. G. Vivas, T. Shih, T. Voss, E. Mazur and C. R. Mendonca, “Nonlinear Spectra of ZnO: Reverse Saturable, Twoand Three-Photon Absorption,” Optics Express, Vol. 18, No. 9, 2010, pp. 9628-9633. doi:10.1364/OE.18.009628
- A M. Suhail, H. J. Kbashi and R. K. Jamal, “Three-Photon Absorption in Nanostructure Wide-Band Gap Semiconductor ZnO Using Femtosecond Laser,” Modern Applied Science, Vol. 5, No. 6, 2011, pp. 199-210. doi:10.5539/mas.v5n6p199
- M. R. Islam and J. Podde, “Optical Properties of ZnO Nanofiber Thin Film Grown by Spray Pyrolysis of Zinc Acetate Precursor,” Crystal Research and Technology, Vol. 44, No. 3, 2009, pp. 286-292. doi:10.1002/crat.200800326
- A. L. Patterson, “The Scherrer Formula for X-Ray Particle Size Determination,” Physical Reviews, Vol. 56, No. 10, 1939, pp. 978-982. doi:10.1103/PhysRev.56.978
- K. Yim and C. Lee, “Optical Properties of Al-Doped ZnO Thin Films Deposited by Two Different Sputtering Methods,” Crystal Research and Technology, Vol. 41, No. 12, 2006, pp. 1198-1202. doi:10.1002/crat.200610749
- C. X. Xu, et al., “Growth and Spectral Analysis of ZnO Nanotubes,” Journal of Applied Physics, Vol. 103, No. 9, 2006, Article ID: 094303. doi:10.1063/1.2908189
- D. D. Wang, J. H. Yang, L. L. Yang, Y. J. Zhang, J. H. Lang and M. Gao, “Morphology and Photoluminescence Properties of ZnO Nanostructures Fabricated with Different Given Time of Ar,” Crystal Research and Technology, Vol. 43, No. 10, 2008, pp. 1041-1045. doi:10.1002/crat.200800109
- K. Alim, V. A. Fonoberov, M. Shamsa and A. A. Balandin, “Micro-Raman Investigation of Optical Phonons in ZnO Quantum Dots,” Journal of Applied Physics, Vol. 97, No. 12, 2005, Article ID: 124313. doi:10.1063/1.1944222
- N. Ashkenov, B. N. Mbenkum, C. Bundesmann, V. Riede, M. Lorenz, D. Spenmann and E. M. Kaidashev, “Infrared Dielectric Functions and Phonon Modes of High-Quality ZnO Film,” Journal of Applied Physics, Vol. 93, No. 1, 2003, pp. 126-133. doi:10.1063/1.1526935H
- H. Richer, Z. P. Wany, “The One Phone Raman Spectrum in Microcrystalline Silicon,” Solid State Communications, Vol. 39, No. 5, 1981, pp. 625-629. doi:10.1016/0038-1098(81)90337-9
- I. H. Chambell and p. M. Fanchet, “Three Effects of Microcrystal Size and Shape on the One Phonon Raman Spectra of Crystalline Semiconductors,” Solid State Communications, Vol. 58, 1986, p. 739.
- J. He, et al., “Three-Photon Absorption in ZnO and ZnS Crystals,” Optics Express, Vol. 13, 2005, pp. 9235-9247.
- R. L. Sutherland, D. G. McLean and S. Kirkpatrick, “Handbook of Nonlinear Optics,” 2nd Edition, Reserved and Expanded, New York, 2003.

