Applied Mathematics
Vol.06 No.08(2015), Article ID:58484,67 pages
10.4236/am.2015.68133
Fourier Coefficients of a Class of Eta Quotients of Weight 16 with Level 12
Barış Kendirli
Istanbul Kultur University, Istanbul, Turkey
Email: baris.kendirli@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 May 2015; accepted 28 July 2015; published 31 July 2015
ABSTRACT
Recently, Williams [1] and then Yao, Xia and Jin [2] discovered explicit formulas for the coef- ficients of the Fourier series expansions of a class of eta quotients. Williams expressed all coefficients of 126 eta quotients in terms of
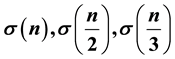 and
and
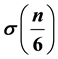 and Yao, Xia and Jin, following the method of proof of Williams, expressed only even coefficients of 104 eta quotients in terms of
and Yao, Xia and Jin, following the method of proof of Williams, expressed only even coefficients of 104 eta quotients in terms of
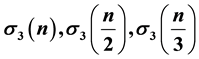 and
and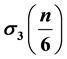 . Here, by using the method of proof of Williams, we will express the even Fourier coefficients of 360 eta quotients i.e., the Fourier coefficients of the sum, f(q) + f(−q), of 360 eta quotients in terms of
. Here, by using the method of proof of Williams, we will express the even Fourier coefficients of 360 eta quotients i.e., the Fourier coefficients of the sum, f(q) + f(−q), of 360 eta quotients in terms of
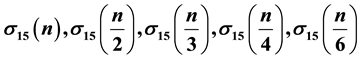 and
and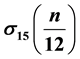 .
.
Keywords:
Dedekind Eta Function, Eta Quotients, Fourier Series

The divisor function
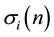 is defined for a positive integer i by
is defined for a positive integer i by
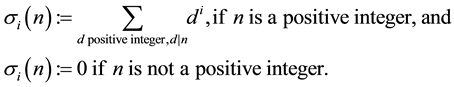 (1)
(1)
The Dedekind eta function is defined by
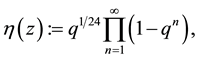 (2)
(2)
where
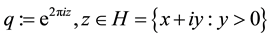 (3)
(3)
And an eta quotient of level n is defined by
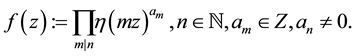 (4)
(4)
It is interesting and important to determine explicit formulas of the Fourier coefficients of eta quotients since they are the building blocks of modular forms of level n and weight k. The book of Köhler [3] (Chapter 3, p. 39) describes such expansions by means of Hecke Theta series and develops algorithms for the determination of suitable eta quotients. One can find more information in [4] -[8] . I have determined the Fourier coefficients of the theta series associated to some quadratic forms, see [9] - [14] .
Recently, Williams, see [1] discovered explicit formulas for the coefficients of Fourier series expansions of a
class of 126 eta quotients in terms of
 and
and . One example is as follows:
. One example is as follows:
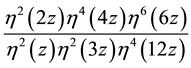
gives the expansion found by Williams.
Then Yao, Xia and Jin [2] expressed the even Fourier coefficients of 104 eta quotients in terms of
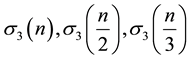 and
and . One example is as follows:
. One example is as follows:
where the even coefficients are obtained. Motivated by these two results, we find that we can express the even Fourier coefficients of 360 eta quotients in terms of


see Table 2. One example is as follows:
We see that the odd Fourier coefficients of 875 eta quotients are zero and even coefficients can be expressed by simple formula. Let
Now we can state our main Theorem:
Theorem 1 Let


Define the integers







They are functions of q by (3). Now define integers
by





Define the rational numbers
and


Table 1. Coefficients of eisenstein series and some eta quotients.
where for
In particular,
for
Proof. It follows from (6)-(11) that


Now we will use p-k parametrization of Alaca, Alaca and Williams, see [15] :

where the theta function

Setting x = p in (12), and multiplying both sides by k16 we obtain
Alaca, Alaca and Williams [16] have established the following representations in terms of p and k:






Therefore, since
we immediately obtain:
It is easy to check the following expressions by (20)-(25)
Obviously,

by [17] . Now
where
So
Therefore, for
since it is easy to see that
hence,
and, for
Remark 2 We have found 360 eta quotients, see Table 2, such that, for
and 875 eta quotients, such that for
Remark 3 If f is an eta quotient, then

are exactly the even coefficients of f. In particular, it means that we have obtained all coefficients of some sum of 360 eta quotients.
Table 2. The eta quotients whose even coefficients can be explicitly calculated.
Remark 4


where




are the unique newforms in



the unique newforms in



Table 3. Expression of fi in terms of newforms.
taking t as a root of

Cite this paper
BarışKendirli, (2015) Fourier Coefficients of a Class of Eta Quotients of Weight 16 with Level 12. Applied Mathematics,06,1426-1493. doi: 10.4236/am.2015.68133
References
- 1. Williams, K.S. (2012) Fourier Series of a Class of Eta Quotients. International Journal of Number Theory, 8, 993-1004.
http://dx.doi.org/10.1142/S1793042112500595 - 2. Yao, O.X.M., Xia, E.X.W. and Jin, J. (2013) Explicit Formulas for the Fourier Coefficients of a Class of Eta Quotients. International Journal of Number Theory, 9, 487-503.
http://dx.doi.org/10.1142/S179304211250145X - 3. Köhler, G. (2011) Eta Products and Theta Series Identities. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-16152-0 - 4. Gordon, B. (1961) Some Identities in Combinatorial Analysis. Quarterly Journal of Mathematics, 12, 285-290.
- 5. Kac, V.G. (1978) Infinite-Dimensional Algebras, Dedekind’s η-Function, Classical Möbius Function and the Very Strange Formula. Advances in Mathematics, 30, 85-136.
http://dx.doi.org/10.1016/0001-8708(78)90033-6 - 6. Macdonald, I.G. (1972) Affine Root Systems and Dedekind’s η-Function. Inventiones Mathematicae, 15, 91-143.
http://dx.doi.org/10.1007/BF01418931 - 7. Zucker, I.J. (1987) A Systematic Way of Converting Infinite Series into Infinite Products. Journal of Physics A, 20, L13-L17.
http://dx.doi.org/10.1088/0305-4470/20/1/003 - 8. Zucker, I.J. (1990) Further Relations amongst Infinite Series and Products: II. The Evaluation of Three-Dimensional Lattice Sums. Journal of Physics A, 23, 117-132.
http://dx.doi.org/10.1088/0305-4470/23/2/009 - 9. Kendirli, B. (2015) Evaluation of Some Convolution Sums by Quasimodular Forms. European Journal of Pure and Applied Mathematics, 8, 81-110.
- 10. Kendirli, B. (2015) Evaluation of Some Convolution Sums and Representation Numbers of Quadratic Forms of Discriminant -135. British Journal of Mathematics and Computer Science, 6, 494-531.
http://dx.doi.org/10.9734/BJMCS/2015/13973 - 11. Kendirli, B. (2014) Evaluation of Some Convolution Sums and the Representation Numbers. Ars Combinatoria, CXVI, 65-91.
- 12. Kendirli, B. (2012) Cusp Forms in and the Number of Representations of Positive Integers by Some Direct Sum of Binary Quadratic Forms with Discriminant -79. Bulletin of the Korean Mathematical Society, 49, 529-572.
http://dx.doi.org/10.4134/BKMS.2012.49.3.529 - 13. Kendirli, B. (2012) Cusp Forms in and the Number of Representations of Positive Integers by Some Direct Sum of Binary Quadratic Forms with Discriminant -47. International Journal of Mathematics and Mathematical Sciences, 2012, Article ID: 303492.
- 14. Kendirli, B. (2012) The Bases of , and the Number of Representations of Integers. Mathematical Problems in Engineering, 2013, Article ID: 695265.
- 15. Alaca, A., Alaca, S. and Williams, K.S. (2006) On the Two-Dimensional Theta Functions of Borweins. Acta Arithmetica, 124, 177-195.
http://dx.doi.org/10.4064/aa124-2-4 - 16. Alaca, A., Alaca, S. and Williams, K.S. (2006) Evaluation of the convolution sums and . Advances in Theoretical and Applied Mathematics, 1, 27-48.
- 17. Gordon, B. and Robins, S. (1995) Lacunarity of Dedekind η-Products. Glasgow Mathematical Journal, 37, 1-14.
http://dx.doi.org/10.1017/S0017089500030329 - 18. Diamond, F. and Shurman, J. (2005) A First Course in Modular Forms. Springer Graduate Texts in Mathematics 228. Springer, New York.





































































































