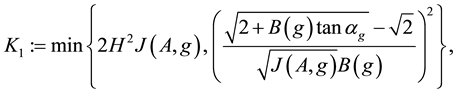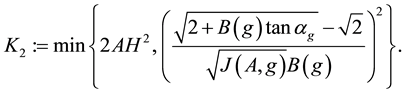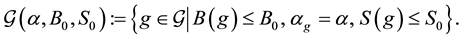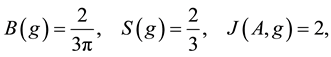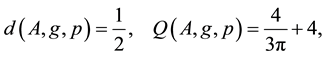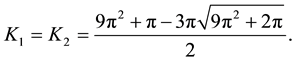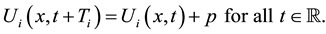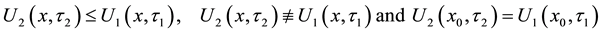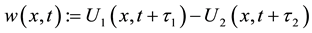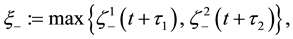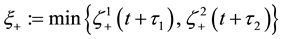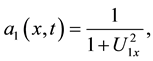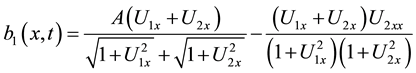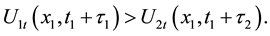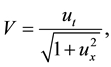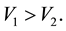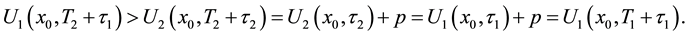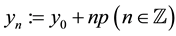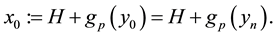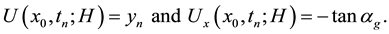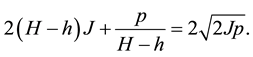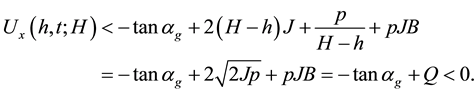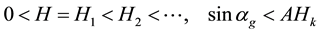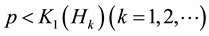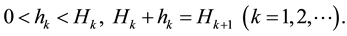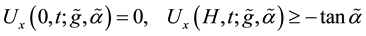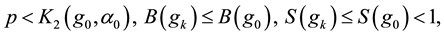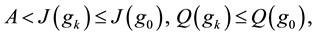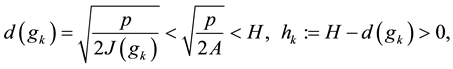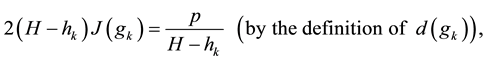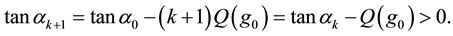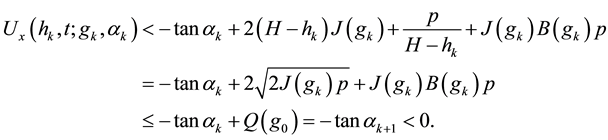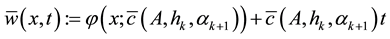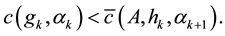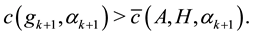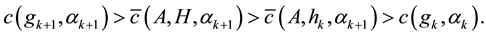Applied Mathematics
Vol.05 No.13(2014), Article ID:47989,9 pages
10.4236/am.2014.513203
Influence of the Domain Boundary on the Speeds of Traveling Waves
Lanxiang Ma1, Jiale Tan2
1Ningbo Shentong Energy Co., Ltd., Ningbo, China
2Department of Mathematics, Tongji University, Shanghai, China
Email: lanxiangma@163.com, jialetan5293@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 April 2014; revised 5 June 2014; accepted 15 June 2014
ABSTRACT
Let H > 0 be a constant, g ≥ 0 be a periodic function and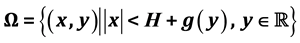 . We consider a curvature flow equation V = κ + A in Ω, where for a simple curve
. We consider a curvature flow equation V = κ + A in Ω, where for a simple curve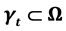 , V denotes its normal velocity, κ denotes its curvature and A > 0 is a constant. [1] proved that this equation has a periodic traveling wave U, and that the average speed c of U is increasing in A and H, decreasing in max g' when the scale of g is sufficiently small. In this paper we study the dependence of c on A, H, max g' and on the period of g when the scale of g is large. We show that similar results as [1] hold in certain weak sense.
, V denotes its normal velocity, κ denotes its curvature and A > 0 is a constant. [1] proved that this equation has a periodic traveling wave U, and that the average speed c of U is increasing in A and H, decreasing in max g' when the scale of g is sufficiently small. In this paper we study the dependence of c on A, H, max g' and on the period of g when the scale of g is large. We show that similar results as [1] hold in certain weak sense.
Keywords:
Curvature Flow Equation, Traveling Wave, Average Speed, Spatial Heterogeneity

1. Introduction
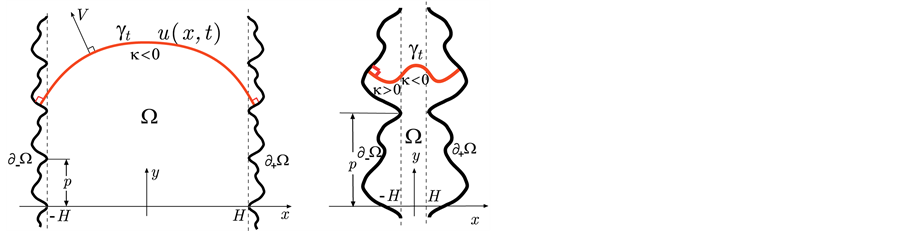
We study traveling waves for a curvature-driven motion of plane curves in a band domain Ω. The law of motion of the curve is given by
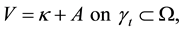 (1)
(1)
where 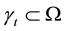 is a simple, smooth curve, V denotes its normal velocity,
is a simple, smooth curve, V denotes its normal velocity, 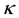 denotes its curvature and A is a positive constant representing a driving force. The band domain Ω is defined as the following. Set
denotes its curvature and A is a positive constant representing a driving force. The band domain Ω is defined as the following. Set
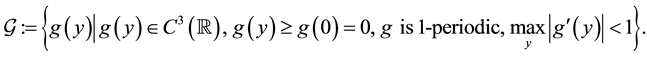 (2)
(2)
For some  we define
we define
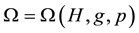

where 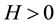 is a constant and
is a constant and 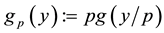 for some
for some 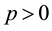 (see Figure 1). Denote the left (resp. right) boundary of Ω by
(see Figure 1). Denote the left (resp. right) boundary of Ω by 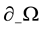 (resp.
(resp. ).
).
By a solution of (1) we mean a time-dependent simple, smooth curve 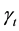 in Ω which satisfies (1) and contacts
in Ω which satisfies (1) and contacts  perpendicularly. Equation (1) appears as a certain singular limit of an Allen-Cahn type nonlinear diffusion equation under the Neumann boundary conditions. The curve
perpendicularly. Equation (1) appears as a certain singular limit of an Allen-Cahn type nonlinear diffusion equation under the Neumann boundary conditions. The curve 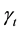
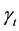
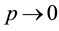
To avoid sign confusion, the normal to the curve 
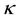
In the case where 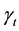

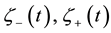


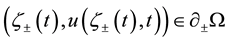
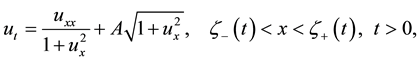
with the boundary conditions
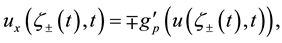
with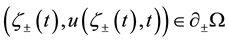
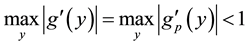
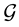
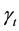

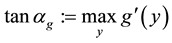
and call 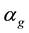
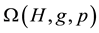
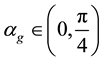
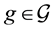
Definition 1 A solution 
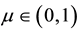

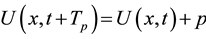


Figure 1. Domain Ω (the left one has fine boundaries, the right one has coarse boundaries).
In [1] the authors proved that, under the condition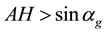
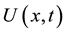
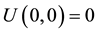
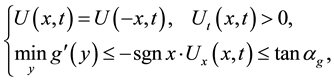
for all 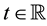
Theorem A (Theorem 2.3 in [1] ). Assume that

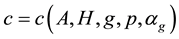
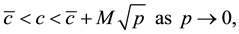
where 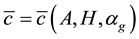
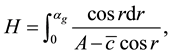
and M is a positive constant independent of p. Moreover 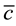
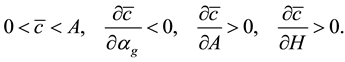
Theorem A gives the dependence of c on A, H and 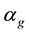
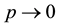
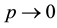
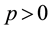

This paper is arranged as the following. In section 2 we list some notations and present our main theorem. In section 3 we prove the main theorem. In subsection 3.1 we prove that 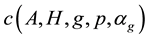
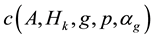

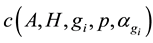
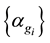
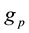
2. Notations and Main Results
We list some notations for convenience. For any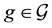
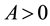
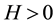
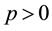
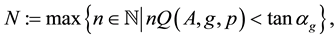
Clearly, N depends on 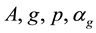

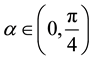
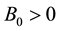
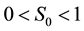
Here is an example, let

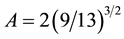
It is easily seen that
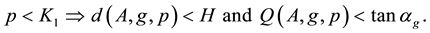
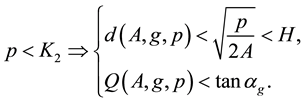
Therefore, if 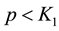
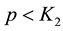
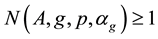
The following is our main result.
Main Theorem. Assume 
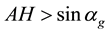
1) 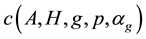
2) if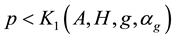
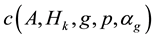
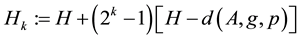
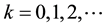
3) if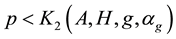
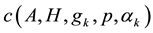
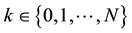

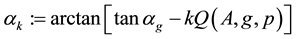
for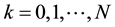
We remark that 3) of the theorem mainly states the dependence of c on 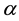
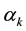
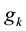
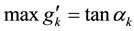
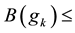
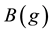
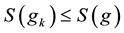
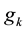
By the main theorem, 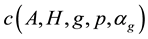
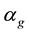

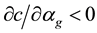
3. Proof of the Main Theorem
In this section, for any two solutions 
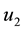
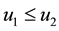
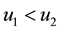
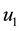
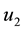
3.1. Proof of Main Theorem 1
Assume that
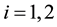

traveling wave of (3)-(4) for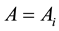
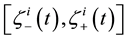
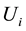

Let 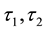
for some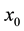
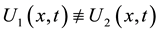
for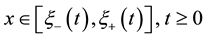
Then 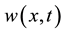
where
are both bounded functions. We show that
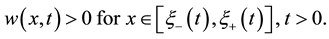
First by the maximum principle (see, for example, Theorem 2 in Chapter 3 in [7] ) we have
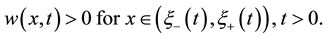
This implies that the graph of 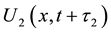
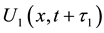
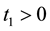
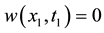
Then
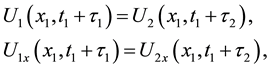
and so
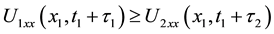
since, otherwise we have 

Using (17), (18), the fact 
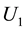
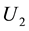
Since the normal velocity V in (1) is expressed by
we see that at the point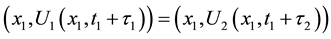
This means that, in a small time-interval around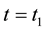

Now taking 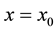
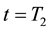
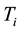
By the fact 


3.2. Dependence of c on H
In this subsection we study the dependence of c on H and prove Main Theorem 2). Since only H is varying, for simplicity, in this part we only indicate H but omit all the other parameters in the notations Ω, U, c, B, J, Ki, ∙∙∙.
Lemma 1 Assume that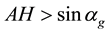
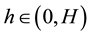
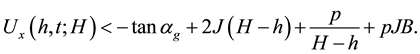
Proof Let 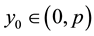
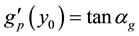
and
Then there exists 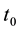
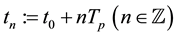
Since 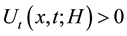
and so

For any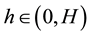
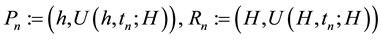
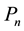
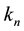
where 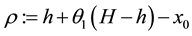

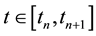


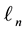
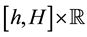
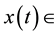

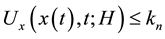
where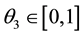
Lemma 2 Assume that 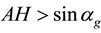

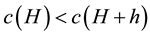
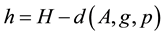
Proof Since 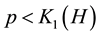
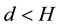
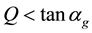
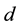
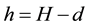

So by Lemma 1 we have
Since 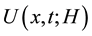
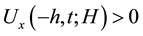
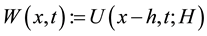
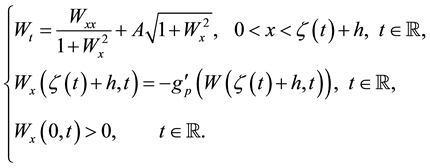
On the other hand, replacing H by 
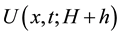
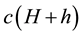
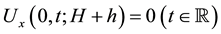

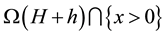


Proof of Main Theorem 2. Set 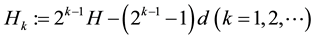
and
by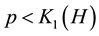
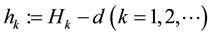
Using Lemma 2 to 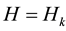

Remark If we take 


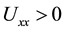
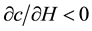
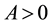
3.3. Dependence of c on g and αg
In this subsection we study the dependence of c on g and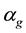
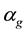

First we note that a classical traveling wave solution of (3) (with a constant speed and a constant profile) is generally written in the form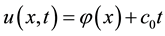
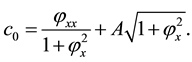
In addition, considering the normalization and the symmetry of Ω, we impose the following initial condition:
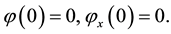
Denote the solution of (22)-(23) by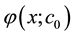
Lemma 3 (Lemma 5.1 in) Assume that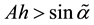
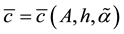

satisfies
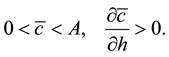
The solution 
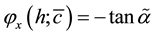
Lemma 4 Let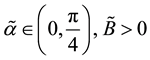
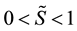
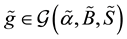
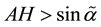
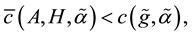
where 

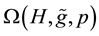
Proof From (7) we see that 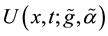
for all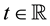
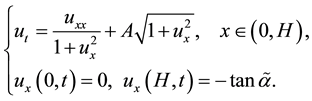
On the other hand, by Lemma 3 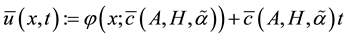
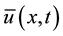

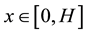
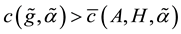
Proof of Main Theorem 3. We write g and 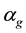
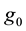
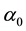
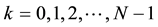
we have
and
By Lemma 1 and the definitions of 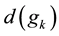
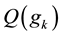
So 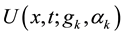

Replacing 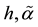
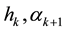
is a classical traveling wave of (28). So we can use comparison principle for 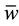
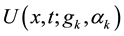
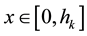
On the other hand, replacing 
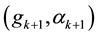
Combining the above inequalities with (25) we have
This proves Main Theorem 3). ,
4. Some Numerical Simulation Results
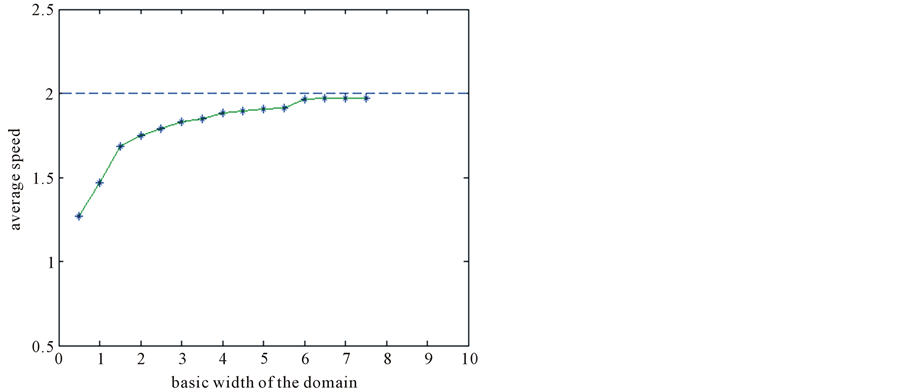
In this section we present some numerical simulation figures. Figure 2 indicates that the average speed c is strictly increasing in the basic width H of the domain.
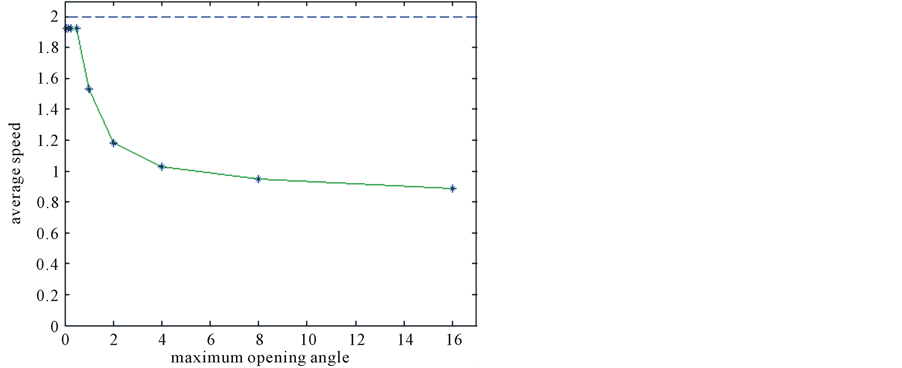
Figure 3 indicates that the average speed c is strictly decreasing in the maximum opening angle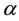
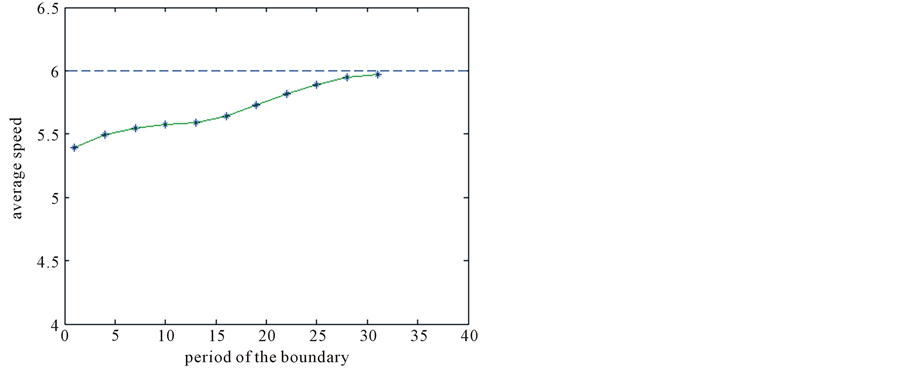
Figure 4 indicates that the average speed c is strictly increasing in the period p of g.
Figure 2. The monotonic dependence of c on H.
Figure 3. The monotonic dependence of c on α.
Figure 4. The monotonic dependence of c on p.
The results shown in Figure 2 and Figure 3 are partially proved in the main theorem. The dependence of c on p is very difficult, and we have no analytic result so far.
References
- Matano, H., Nakamura, K.I. and Lou, B. (2006) Periodic Traveling Waves in a Two-Dimensional Cylinder with Saw- Toothed Boundary and Their Homogenization Limit. Networks and Heterogeneous Media, 1, 537-568. http://dx.doi.org/10.3934/nhm.2006.1.537
- Alfaro, M., Hilhorst, D. and Matano, H. (2008) The Singular Limit of the Allen-Cahn Equation and the FitzHugh-Na- gumo System. Journal of Differential Equations, 245, 505-565. http://dx.doi.org/10.1016/j.jde.2008.01.014
- Lou, B. (2007) Singular Limits of Spatially Inhomogeneous Convection-Reaction-Diffusion Equation. Journal of Statistical Physics, 129, 509-516. http://dx.doi.org/10.1007/s10955-007-9400-3
- Nakamura, K.I., Matano, H., Hilhorst, D. and Schatzle, R. (1999) Singular Limits of Spatially Inhomogeneous Convection-Reaction-Diffusion Equation. Journal of Statistical Physics, 95, 1165-1185. http://dx.doi.org/10.1023/A:1004518904533
- Cioranescu, D. and Donato, P. (1999) An Introduction to Homogenization. Oxford University Press, Oxford.
- Cioranescu, D. and Saint Jean Paulin, J. (1999) Homogenization of Reticulated Structures. Springer-Verlag, New York.
- Protter, M.H. and Weinberger, H.F. (1967) Maximum Principles in Differential Equations. Prentice Hall, Englewood Cliffs, 172-173.