ABSTRACT

The nullity of a graph is the multiplicity of the eigenvalue zero in its spectrum. In this paper we show the expression of the nullity and nullity set of unicyclic graphs with n vertices and girth r, and characterize the unicyclic graphs with extremal nullity.

Keywords:

Eigenvalues (of Graphs), Nullity, Unicyclicgraphs

1. Introduction

Let 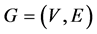be a simple undirected graph with n vertices. The disjoint union of two graphs G₁ and G₂ is denoted by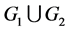. The null graph of order n is the graph with n vertices and no edges. As usual, the star, path, cycle and the complete graph of order n are denoted by S_n, P_n, C_n and K_n, respectively. An isolated vertex is sometimes denoted by K₁.

Let A(G) be the adjacency matrix of G. The eigenvalues 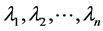of A(G) are said to be the eigenvalues of G, and to form the spectrum of this graph. The number of zero eigenvalues in the spectrum of the graph G is

called its nullity and is denoted by η(G). Let r(G) be the rank of A(G). Clearly,.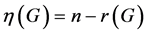

A graph is said to be singular (nonsingular) if its adjacency matrix A(G) is a singular (nonsingular) matrix.

In [1] , L. Collatz and U. Sinogowitz first posed the problem of characterizing all graphs which satisfying. This question is of great interest in chemistry, because, as has been shown in [2] , for a bipartite graph

G (corresponding to an alternant hydrocarbon), if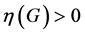, then it indicates the molecule which such a graph

represents is unstable. The nullity of a graph is also important in mathematics, since it is related to the singularity of A(G). The problem has not yet been solved completely. Some results on trees and it’s line graphs, bipartite graphs, unicyclic graphs, bicyclic graphs and tricyclic graphs are known (see [3] - [14] ). For details and further references we see [15] [16] .

A unicyclic graph is a simple connected graph in which the number of edges equals the number of vertices.

The length of the shortest cycle in a graph G is called the girth of G, denoted by g(G). If G is a unicyclic graph, then the girth of G is the length of the only cycle in G.

Let U_n be the set of all unicyclic graph with n vertices and let U(n, r) be the set of all unicyclic graphs with n vertices and girth r. A subset N of {0, 1, 2, ..., n} is said to be the nullity set of U(n, r) provided that for any kÎN, there exists at least one graph such that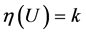, and no k Ï N satisfies this property.

A matching of G is a set of independent edges of G, a maximal matching is a matching with maximum possible number of edges. The collection of all maximal matching is denoted by M(G), for any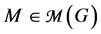, the size of M, i.e., the maximum number of independent edges in G, is denoted by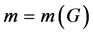. If n is even and, then we call the maximal matching a perfect matching of G, shot for PM.

It is difficult to give an expression of the nullity of a graph, so many papers give that the upper bound of the nullity of some specific graphs and characterized the extremal graphs attaining the upper bound (see [6] [9] [11] [12] [14] [17] ). For the trees we know the following concise formula:

Theorem 1.1 [3] If t is a tree with n vertices and m is the size of its maximal matchings, then its nullity is equal to.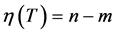

Theorem 1.1 implies to 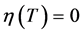if and only if T is a PM-tree.

In this paper we show the expression of the nullity and nullity set of unicyclic graphs with n vertices and girth r, and characterize the unicyclic graphs with extremal nullity. For terminology and notation not defined here we refer to [3] .

2. Some Lemmas

The following lemmas are needed, Lemmas 2.1 and Lemma 2.3 are clear.

Lemma 2.1 Let H be an induced subgraph of G. Then,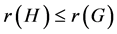

Lemma 2.2 Let H be an induced subgraph of G. Then.

Proof..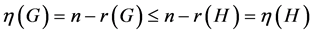

Lemma 2.3 Let, then,

where are connected components of G.

Lemma 2.4 [14]

Let, if r = n, then by Lemma 2.4 we have

Lemma 2.5

So we discuss that r < n in the following unicyclics. Let U₀(n, r) be the set of all unicyclic graphs with n vertices and girth r and r < n, let U_0,1(n, r) be the subset of U₀(n, r) with odd girth r and let U_0,2(n, r) be the subset

of U₀(n, r) with even girth r, clearly and.

Lemma 2.6 [3] For a graph G containing a vertex of degree 1, if the induced subgraph H (of G) is obtained by deleting this vertex together with the vertex adjacent to it, then the relation holds.

The characteristic polynomial of graph G is denoted by

(1)

Lemma 2.7 [3] Let. Then the coefficient of x^n-i is

. (2)

where the sum is over all subgraphs H of G consisting of disjoint edges and cycles, and having i vertices. If H is such a subgraph then k(H) is the number of components in it and c(H) is the number of cycles.

Let in (2), then, where H is spanning subgraphs of G consisting of disjoint

edges and cycles.

3. Main Results

In [18] , Ashraf and Bamdad considered the opposite problem: which graphs have nullity zero? Clearly, for a graph G, if and only if and if and only if in (1). So by (1) we have following theorem, that is

Theorem 3.1 For a graph G,

1) if and only if,

2) if and only if.

where the sum is over all spanning subgraphs H of G consisting of disjoint edges and cycles.

Proof. By (1) it is clear.

By (1) we know also that if and only if there exist, such that and

(Note that and). So we have

Corollary 3.1 For a graph G, if and only if for

and for in (2).

Let U be a unicyclic graph with girth r, Let H be a subgraphs of U consisting of disjoint edges and cycles with maximum possible number of vertices. Let H be the collection of all H. Since U is unicyclic graph, then H have

two types: and m(U)P₂, where C_r is induced subgraph of U and mP₂ is disjoint union of

m edges P₂. Let and, clearly and

. If, then.

Since U doesn’t contains a subgraph G₁ consisting of disjoint edges and cycles, such that

, hence for,

. So we have

Corollary 3.2 Let U be a unicyclic graph with girth r, then if and only if

, where.

Theorem 3.2 Let, then

1) there exist, for any r/2 edges in M, such that they not all belong to E(C_r);

2) for any, there exist r/2 edges in M, such that they all belong to E(C_r).

Where C_r is induced subgraph of U.

Proof. Let and let C_r be an induced subgraph of U. By Corollary 2.2, we only need to discuss

that whether equals zero. We give a sign for the edges of C_r, in nature order.

Case 1.. Since is odd and

is even, , hence either or. If,

then and. Since for all, they have the same number of component, hence

, where. If, then

and. Similarly, , where. Thus

.

Case 2..

Subcase 2.1 There exist, where. In this case, the

and

, where the in H₀, H₁ and

H₂ are same, and we call H₁ and H₂ are conjugate subgraph of H₀. Since r/2 is odd, hence for any HÎH, the

number of component of H have the same odevity, hence, where.

Subcase 2.2 There doesn’t exist. In this case, since all and they have the same edges,

hence, where. So.

Case 3. and there exist, for any r/2 edges in M, such that they not all belong to E(C_r).

Subcase 3.1 There exist H₀ÎH₁, where. In this case, the

and

. Let. For,

we have

.

Since we know that there exist, for any r/2 edges in M, such that they not all belong to E(C_r),

hence we assume that and for any r/2 edges in H₃, such that they not all belong to

E(C_r). Except H₃, if there exist others (i ≥ 4) and for any r/2 edges in H_i (i ≥ 4), such that they not all belong to E(C_r), then we have

and, so.

Subcase 3.2 There aren’t exist. In this case, similar to Subcase 2.2 of Case 2, we have.

Case 4. r ≡ 0(mod 4) and for any, there exist r/2 edges in M, such that they all belong to E(C_r).

In this case, for any, let, where

is independent edges in C_r. For the same with H₁, let

and, where

is also independent edges in C_r, then and. In fact, in this case for any one, there

exist a conjugate graph of H′, such that, where H′ and H′′ are conjugate subgraphs of H,

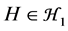
that is and. Similarly, for any one, it corres-

ponding two conjugate subgraphs. So

,

where. Since if, thus we consider the subgraph

H of U consisting of disjoint edges and cycles, and having m(U) ? 1 edges. Clearly there exist a

(m(U) ? 1)-matching, such that there exist r/2 − 1 edges belong in E(C_r) and edges belong in

. Similar to Case 3, , where. So

.

Let C_r be a cycle and let P_n−r be a path. Suppose that v is a vertex of C_r and u is a pendant vertex of P_n−r. Joining v and u by an edge, the resulting graph (Figure 1) is denoted by U(r, n ? r).

Corollary 3.3 Let, then

Proof. Since, hence U contains an induced subgraph U(r, 1) (see Figure 1).

Case 1.. In this case, by Theorem 2.2 we have

, by Lemma 2.2 we

have.

Case 2.. In this case, if, by Theorem 2.2 we have

. If, then there exist, such that the pen-

dant edge belong to M, that is for any r/2 edges in M, it not all belong to E(C_r), so

, by Lemma 2.2 we have.

Let if r is odd and letif r is even in Corollary 2.3, and combine to Lemma 2.7 we have

Corollary 3.4 [18] For any (n ≥ 5),.

Corollary 3.5 Let, then if and only if n is even and U contains PM or n is odd and contains PM.

Proof. Let, where r is odd.

“⇒” If, then by Theorem 2.2 we have.

Case 1. If n is even, then, U contains PM.

Case 2. If n is odd, then, , contains PM.

“⇐”

Case 1. If n is even and U contains PM, then, by Theorem

2.2, η(U) = 0.

Case 2. If n is odd and contains PM, then

, by Theorem 2.2,.

Corollary 3.6 Let, then if and only if and U contains PM or

and U contains PM, and for any r/2 edges in the PM, such that they not all belong to E(C_r).

Proof. Let, where r is even.

“⇒” If, then by theorem 2.2 we have or. If

, then, a contradiction. So we have, U contains PM. Since r

is even, hence or. If, then there exist PM, for any r/2 edges in the

PM, such that they not all belong to E(C_r). Otherwise, by Theorem 2.2 we have, a contradiction.

“⇐”

Case 1. If and U contains PM, then by Theorem 2.2 we have.

Case 2. If and U contains PM, and for any r/2 edges in the PM, such that it not all belong to E(C_r), then by Theorem 2.2 we have.

An edge belonging to a matching of a graph G is said to cover its two end-vertices. A vertex v is said to be perfectly covered (PC) if it is covered in all maximal matching of G [7] .

Any vertex adjacent to a pendent vertex is a PC-vertex. However, there may be exist PC-vertices adjacent to no pendent vertex. For instance, the central vertex in the path on an odd number of vertices is PC.

Let be the PC-vertices of C_r. Let be a graph is obtained from C_r, by adding r_i

pendant edges in the PC-vertex of C_r, respectively. Where

. The degree of PC-vertices of needn’t equality, even for some PC-vertices, no pendant

vertex joint to the PC-vertex, but the sum of number of all pendant vertices is n ? r. For r = 5 and 6, an and

see Figure 2, the PC-vertices are indicated by numbers 1, 2, 3.

Let be the set of all, where r is odd and let be the set of all, where r is even.

Clearly and. For any (i = 1, 2), the PC-vertices of

C_r is also the PC-vertices of U, where C_r is inducted subgraph of U.

Let d(v, G) denote the distance from a vertex v to the graph G, if vÎV(G), then.

Corollary 3.7 Let, then if and only if.

Proof. Since, hence r is odd.

“⇒” Let, if, by Theorem 2.1 we have

. Since r is odd, hence, , so for any

pendant v of U,. Otherwise, , a contradiction. If there exist at least one pendant

vertex v in U, such that, then there exist at least one independent edge in, so

, , a contradiction.

So for any pendant vertex of U,. Since there exist (r+1)/2 PC-vertices in C_r, if there exist pendant

edges for every vertices of C_r in U, then, a contradic-

tion. Hence there exist pendant edges for part of vertices of C_r in U. If there exist (r+1)/2 + 1 vertices in C_r such

that every vertex have pendant edges, then, a con-

tradiction. So there exist at most (r+1)/2 vertices, such that every vertex have pendant edges, that is all pendant

vertices of U joint to at most (r+1)/2 vertices in C_r. In the neighbor vertices of all pendant vertices of U, if there

exist (r?1)/2 PC-vertices and one non PC-vertex of C_r, then

, a contradiction.

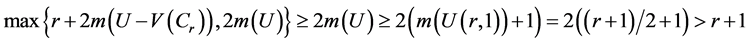
Thus all pendant vertices of U are joint to the PC-vertices of C_r, thus.

“⇐” Let (see Figure 2), since r is odd, and, hence

, by Theorem 2.1, we have

.

Let u be a vertex of C_r, and let v be a k-degree vertex of K_1,k+1. Joining u and v by a path P_l, the resulting graph is denoted by U(r, l, k + 1), where. When l = 2, we get U(r, 2, k + 1) (Figure 3).

For convenience, we call the star in U(r, 2, k + 1) is pendant star. Let U′(r, l, k) be a unicyclic graph come from U(r, l, k + 1), by removing a pendant edge and adding it to another vertex of C_r, where r + l + k = n (See Figure 4).

Corollary 3.8 Let, then if and only if or

and

Proof. Since, hence r is even.

“⇒” Let, if, by Theorem 2.2 we have or.

Case 1.. In this case, since r is even, hence for any pendant v of U,. Otherwise,

, a contradiction. For an edge, If u and v both have at lest one pendant edge in U,

respectively. Then, a contradiction. So all pendant vertices of U join to some PC-vertices of U,

thus.

Case 2.. In this case, since r is even, hence for any one pendant v of U,

. Otherwise, , a contradiction.

Subcase 2.1. There exist vÎU, such that. In this case, U(n, 3) (see Figure 1) is an induced sub-

graph of U, then there exist, such that the pendant edge belong to M, so for any r/2 edges in

M, it not all belong to E(C_r), by Theorem 2.1 we have, by Lemma 2.2,

, a contradiction.

Subcase 2.2. There exist vÎU, such that. In this case, U(r, 2, k +1) (see Figure 3, specially take k=0) is an induced subgraph of U, and only one vertex of U have only one pendant star. Otherwise, a contradiction. If there exist at lest one pendant edge in other one vertex of C_r, the resulting graph is denoted by U′(r, 2, k) (see Figure 4). Since there exist, such that the two inde-

pendent pendant edges in (U′(r,2,k)) belong to M, we know that, hence for any r/2

edges in M, they not all belong to E(C_r), by Lemma 2.2 and Theorem 2.2 we have

, a contradiction. So (see Figure 3).

If, by Theorem 2.2 we have, a contradic-

tion. So and.

“⇐” Case 1. Let (see Figure 2), since r is even, hence. If, then by

Theorem 2.1 we have. If, since r < n, hence U contains a induced

subgraph U(r, 1) (see Figure 1), for a, let the pendant edge of U(r, 1) belong to the M, then

the r/2 edges in M, not all belong to E(C_r), by Theorem 2.2 we have.

Case 2. Let and, then. Since for any

, there exist r/2 edges in M, such that they all belong to E(C_r), by Theorem 2.1 we have

.

Let l = 1 in U(r, l, k+1) (Figure 3), we get the following graph U(r, 1, k +1) (Figure 5).

Theorem 3.3 The nullity set of U_0,1(n, r) is {0, 1, 2, ..., n-r-1}.

Proof. By Corollary 2.3, we only need to show that for each, there exist a unicyclic

graph such that, where r is odd.

Case 1.. Let (see Figure 1). If, using Lemma 2.6, after (n − r)/2 steps,

we get C_r, by Lemma 2.6 and 2.5 we have. If, using Lemma 2.6, af-

ter (n − 2)/2 steps, we get a P₂, by Lemmas 2.6 we have.

Case 2.. Let (see Figure 5), where, using Lemma 2.5, after

(r+1)/2 steps, we get kK₁, by Lemmas 2.3 we have.

Case 3.. Let (see Figure 3), where. If, Us-

ing Lemma 2.6, after l/2 steps, we get, by Lemmas 2.3 and 2.5 we have

. Similarly, If, we have

.

Theorem 3.4 The nullity set of U_0,2(n, r) is.

Proof. Similar to Theorem 2.3, if, we consider the graph U(r, l, k) with k pendants (see Figure 3

), where. If, we consider the graph U′(r, l, k) with k pendants (see Figure 4),

where.

If we take in Theorem 2.3 and in Theorem 2.4, then we have the following Corollary:

Corollary 3.9 [18] The nullity set of U_n is.

Acknowledgements

This work is supported by the Natural Science Foundation of Qinghai Province (Grant No. 2011-Z-911).

Cite this paper

Shengbiao Hu, (2014) A Note on the Nullity of Unicyclic Graphs. Applied Mathematics,05,1623-1631. doi: 10.4236/am.2014.510156

References