Applied Mathematics
Vol.4 No.1(2013), Article ID:27243,12 pages DOI:10.4236/am.2013.41026
Some Lp Inequalities for B-Operators
Department of mathematics, University of Kashmir, Harzarbal, Sringar, India.
Email: dr.narather@gmail.com, ahangarsajad@gmail.com
Received November 8, 2012; revised December 8, 2012; accepted December 15, 2012
Keywords: 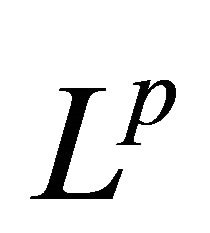 -Inequalities;
-Inequalities; 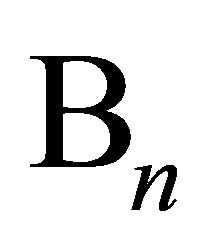 -Operators; Polynomials
-Operators; Polynomials
ABSTRACT
If 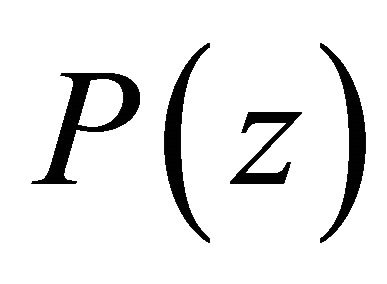 is a polynomial of degree at most n having all its zeros in
is a polynomial of degree at most n having all its zeros in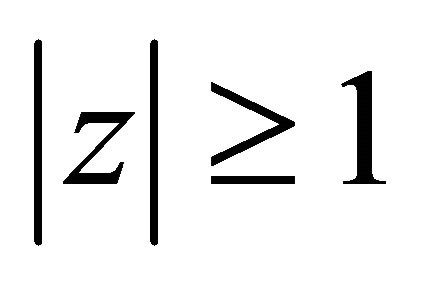 , then it was recently claimed by Shah and Liman ([1], estimates for the family of $B$-operators, Operators and Matrices, (2011), 79-87) that for every
, then it was recently claimed by Shah and Liman ([1], estimates for the family of $B$-operators, Operators and Matrices, (2011), 79-87) that for every ,
, 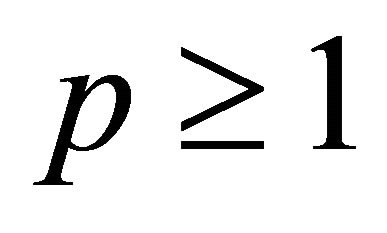 ,
, 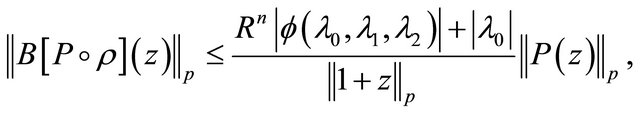 where
where 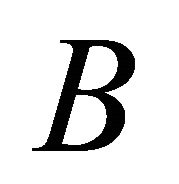 is a
is a  -operator with parameters
-operator with parameters 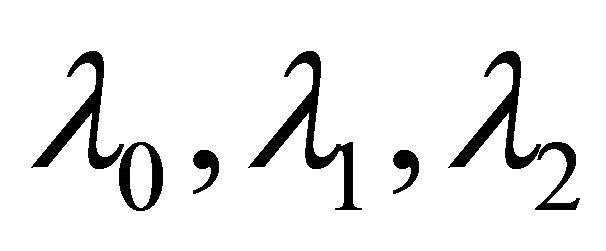 in the sense of Rahman [2],
in the sense of Rahman [2],  and
and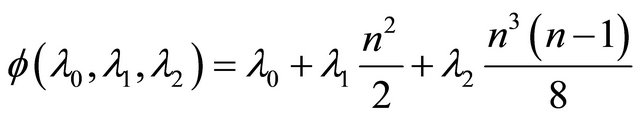 . Unfortunately the proof of this result is not correct. In this paper, we present certain more general sharp Lp-inequalities for
. Unfortunately the proof of this result is not correct. In this paper, we present certain more general sharp Lp-inequalities for 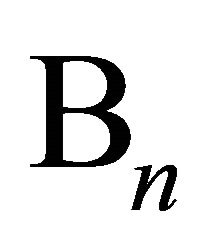 -operators which not only provide a correct proof of the above inequality as a special case but also extend them for
-operators which not only provide a correct proof of the above inequality as a special case but also extend them for 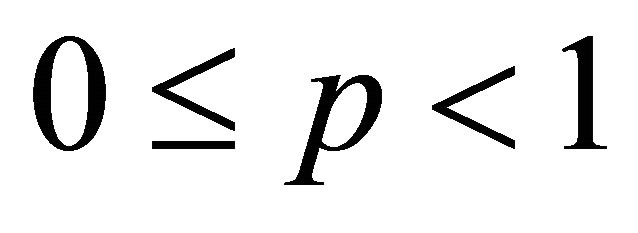 as well.
as well.
1. Introduction and Statement of Results
Let 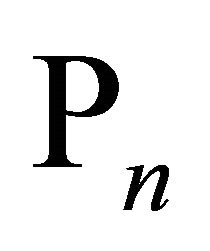 denote the space of all complex polynomials
denote the space of all complex polynomials
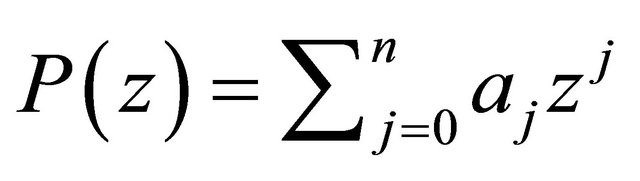 of degree at most
of degree at most![]() . For
. For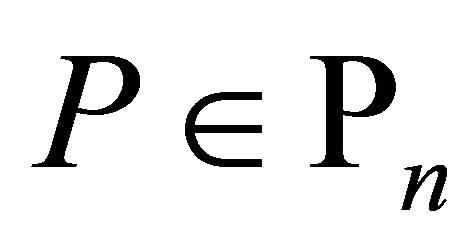 define
define
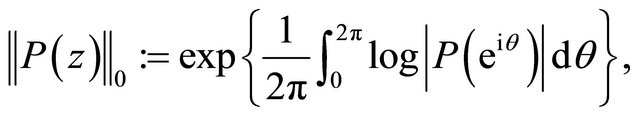
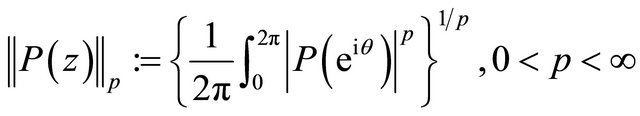

and denote for any complex function 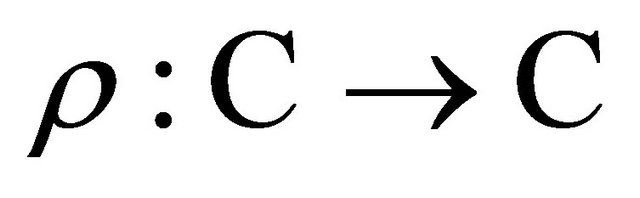 the composite function of
the composite function of  and
and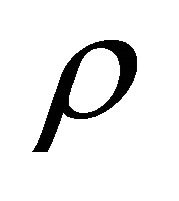 , defined by
, defined by 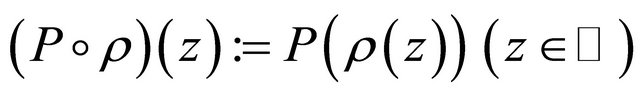 , as
, as .
.
A famous result known as Bernstein’s inequality (for reference, see [3, p. 531], [4, p. 508] or [5] states that if , then
, then
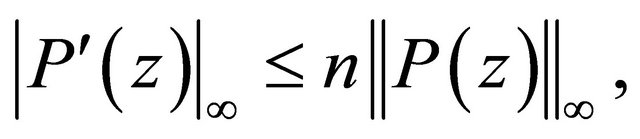 (1.1)
(1.1)
whereas concerning the maximum modulus of 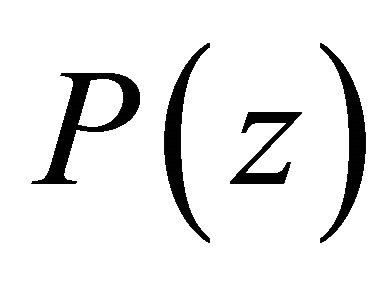 on the circle
on the circle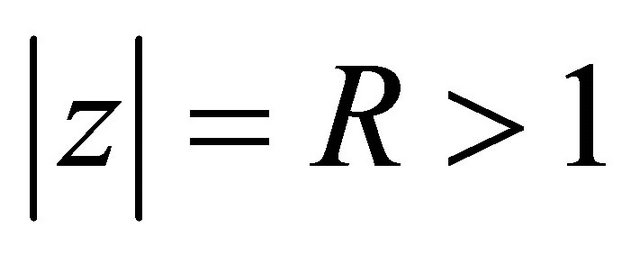 , we have
, we have
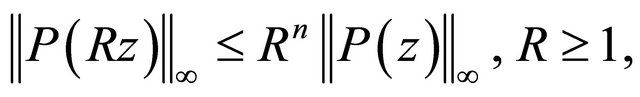 (1.2)
(1.2)
(for reference, see [6, p. 442] or [3, Vol. 1, p. 137]).
Inequalities (1.1) and (1.2) can be obtained by letting  in the inequalities
in the inequalities
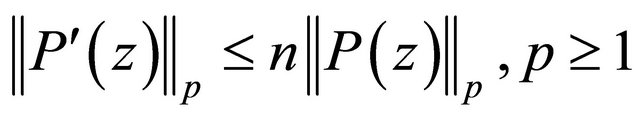 (1.3)
(1.3)
and
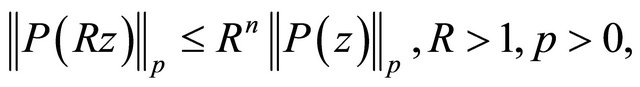 (1.4)
(1.4)
respectively. Inequality (1.3) was found by Zygmund [7] whereas inequality (1.4) is a simple consequence of a result of Hardy [8] (see also [9, Th. 5.5]). Since inequality (1.3) was deduced from M. Riesz’s interpolation formula [10] by means of Minkowski’s inequality, it was not clear, whether the restriction on p was indeed essential. This question was open for a long time. Finally Arestov [11] proved that (1.3) remains true for 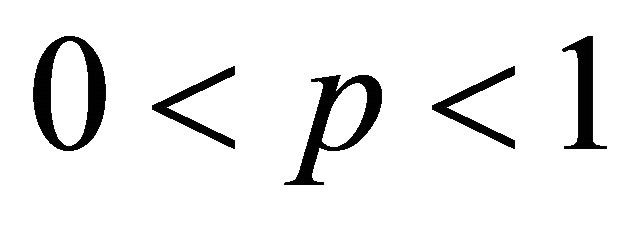 as well.
as well.
If we restrict ourselves to the class of polynomials 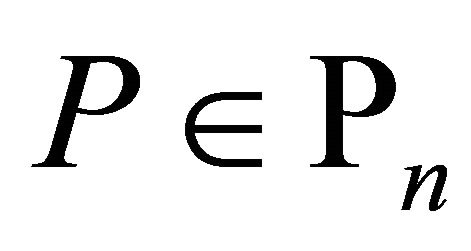 having no zero in
having no zero in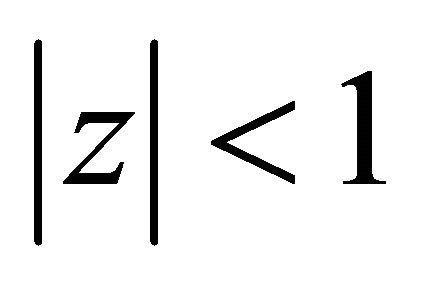 , then Inequalities (1.1) and (1.2) can be respectively replaced by
, then Inequalities (1.1) and (1.2) can be respectively replaced by
 (1.5)
(1.5)
and
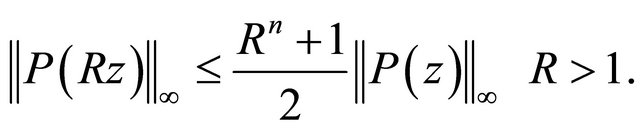 (1.6)
(1.6)
Inequality (1.5) was conjectured by Erdös and later verified by Lax [12], whereas Inequality (1.6) is due to Ankey and Ravilin [13].
Both the Inequalities (1.5) and (1.6) can be obtain by letting  in the inequalities
in the inequalities
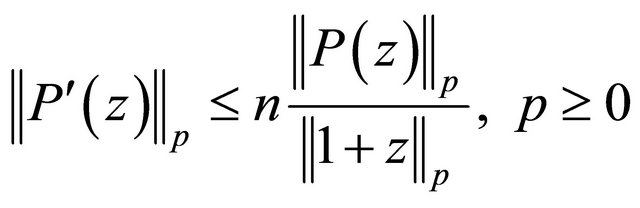 (1.7)
(1.7)
and for 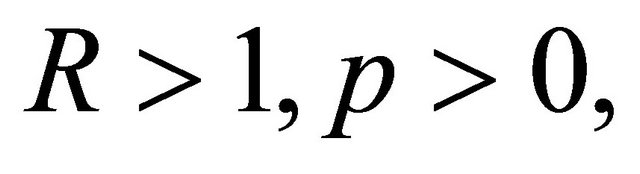
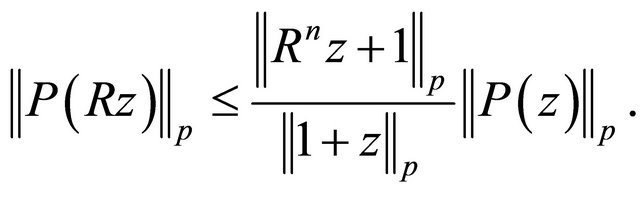 (1.8)
(1.8)
Inequality (1.7) is due to De-Bruijn [14] for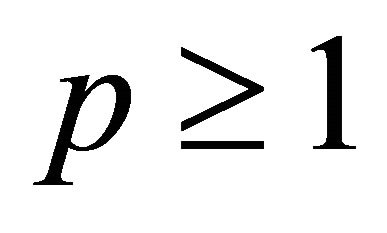 . Rahman and Schmeisser [15] extended it for
. Rahman and Schmeisser [15] extended it for  whereas the Inequality (1.8) was proved by Boas and Rahman [16] for
whereas the Inequality (1.8) was proved by Boas and Rahman [16] for 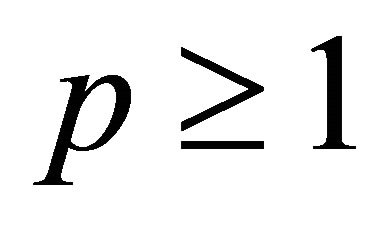 and later it was extended for
and later it was extended for 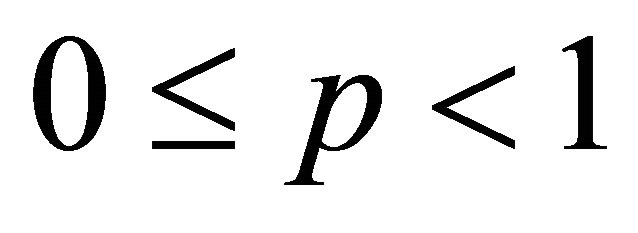 by Rahman and Schmeisser [15].
by Rahman and Schmeisser [15].
Q. I. Rahman [2] (see also Rahman and Schmeisser [4, p. 538]) introduced a class 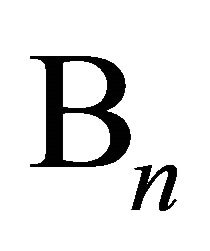 of operators
of operators 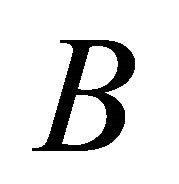 that carries a polynomial
that carries a polynomial 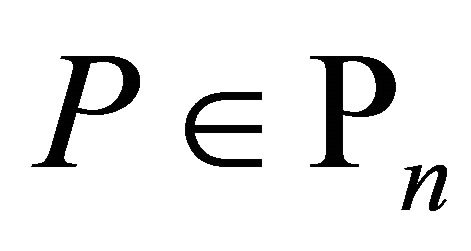 into
into
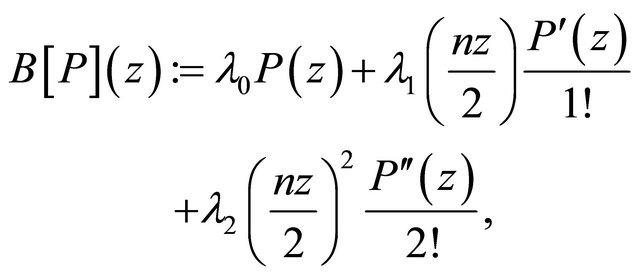 (1.9)
(1.9)
where 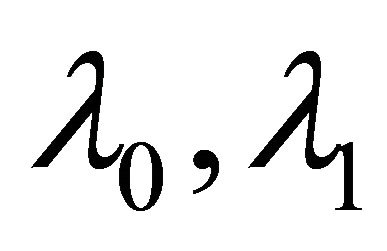 and
and 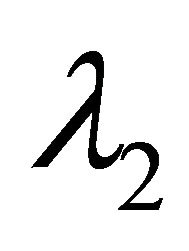 are such that all the zeros of
are such that all the zeros of
 (1.10)
(1.10)
where  lie in half plane
lie in half plane

As a generalization of Inequality (1.1) and (1.5), Q. I. Rahman [2, inequality 5.2 and 5.3] proved that if  and
and  then for
then for 
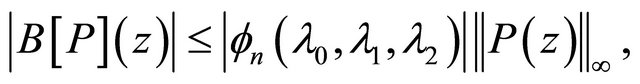 (1.11)
(1.11)
and if 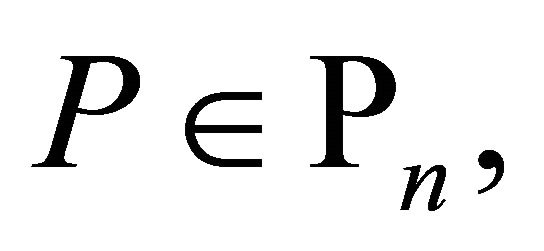
 in
in  then
then 
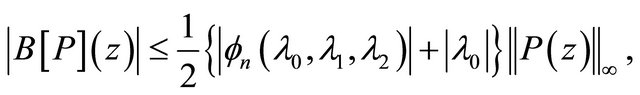 (1.12)
(1.12)
where
 (1.13)
(1.13)
As a corresponding generalization of Inequalities (1.2) and (1.4), Rahman and Schmeisser [4, p. 538] proved that if 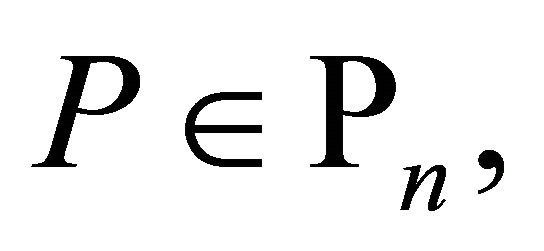 then
then 
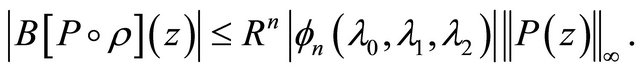 (1.14)
(1.14)
and if 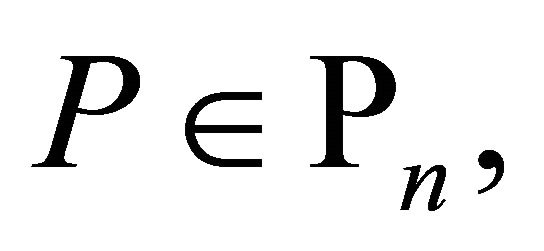
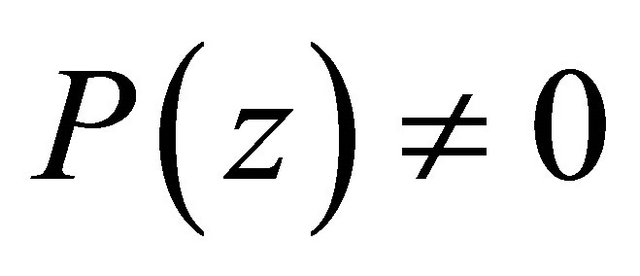 in
in  then as a special case of Corollary 14.5.6 in [4, p. 539], we have
then as a special case of Corollary 14.5.6 in [4, p. 539], we have
 (1.15)
(1.15)
where 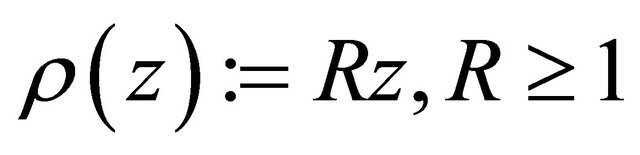 and
and 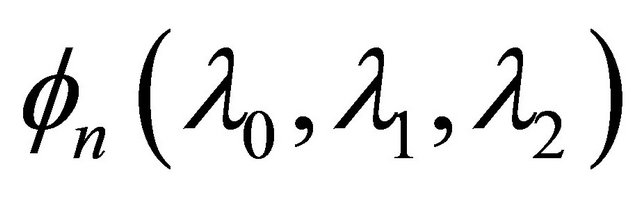 is defined by (1.13).
is defined by (1.13).
Inequality (1.15) also follows by combining the Inequalities (5.2) and (5.3) due to Rahman [2].
As an extension of Inequality (1.14) to 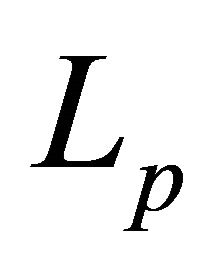 -norm, recently Shah and Liman [1, Theorem 1] proved:
-norm, recently Shah and Liman [1, Theorem 1] proved:
Theorem A. If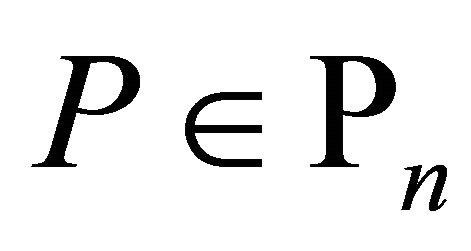 , then for every
, then for every 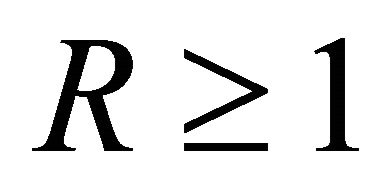 and
and ,
,
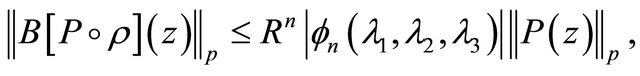 (1.16)
(1.16)
where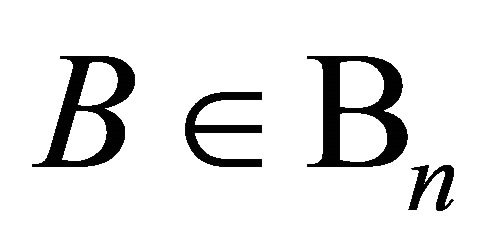 ,
, 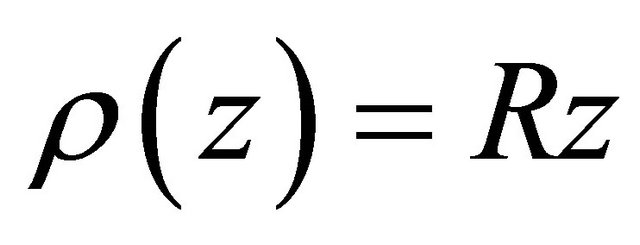 and
and 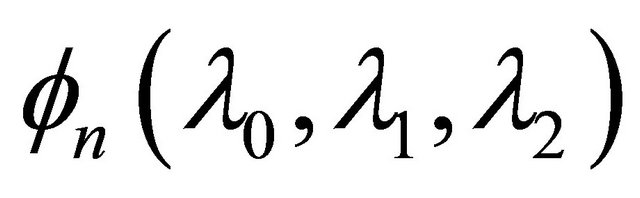 is defined by (1.13).
is defined by (1.13).
While seeking the analogous result of (1.15) in  norm, they [1, Theorem 2] have made an incomplete attempt by claiming to have proved the following result:
norm, they [1, Theorem 2] have made an incomplete attempt by claiming to have proved the following result:
Theorem B. If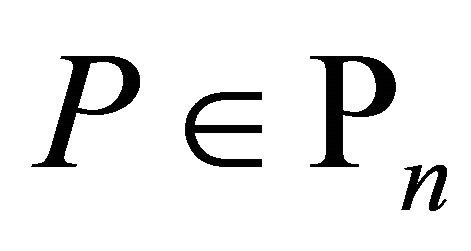 , and
, and 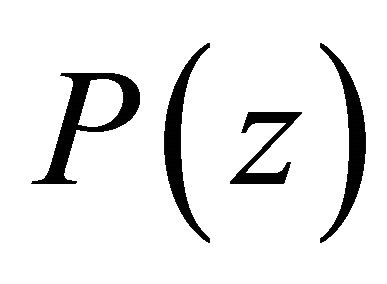 does not vanish for
does not vanish for 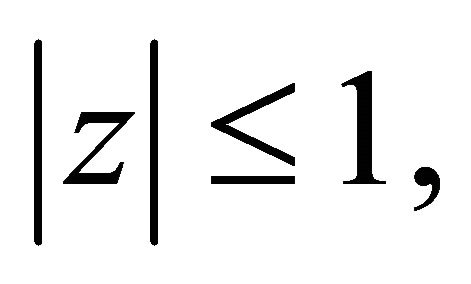 then for each
then for each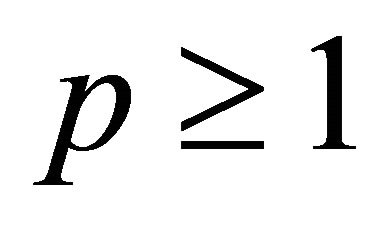 ,
,  ,
,
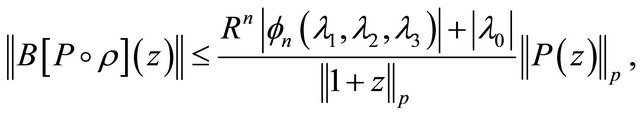 (1.17)
(1.17)
where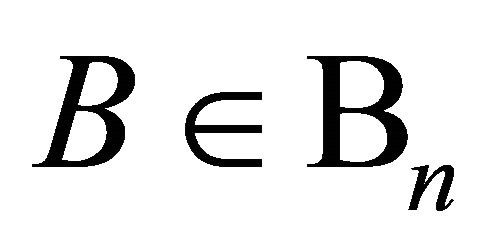 ,
,  and
and 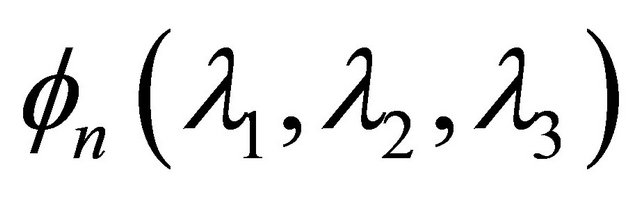 is defined by (1.13).
is defined by (1.13).
Further, it has been claimed in [1] to have proved the Inequality (1.17) for self-inversive polynomials as well.
Unfortunately the proof of Inequality (1.17) and other related results including the key lemma [1, Lemma 4] given by Shah and Liman is not correct. The reason being that the authors in [1] deduce:
1) line 10 from line 7 on page 842) line 19 on page 85 from Lemma 3 [1] and3) line 16 from line 14 on page 86by using the argument that if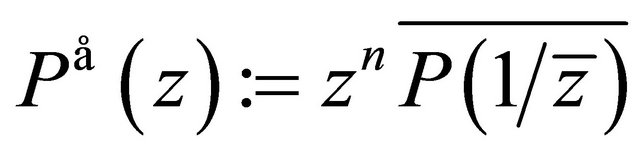 , then for
, then for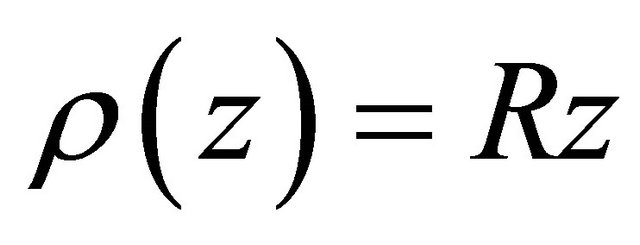 ,
, 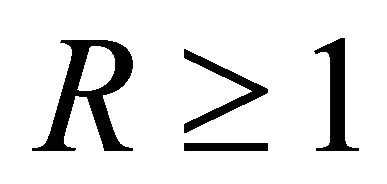 and
and 
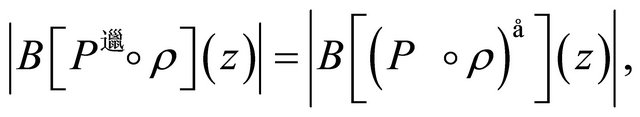
which is not true, in general, for every  and
and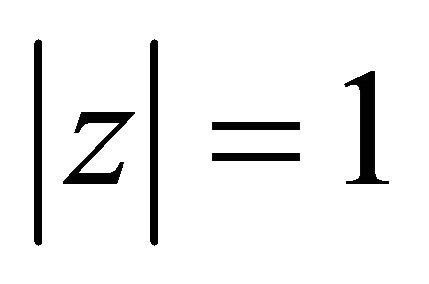 . To see this, let
. To see this, let
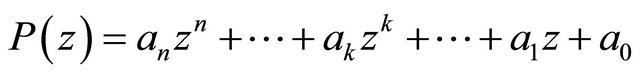
be an arbitrary polynomial of degree![]() , then
, then
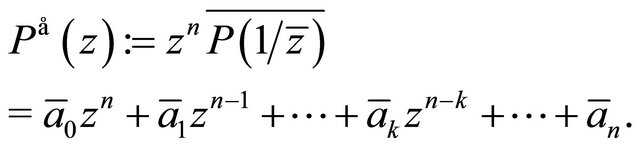
Now with 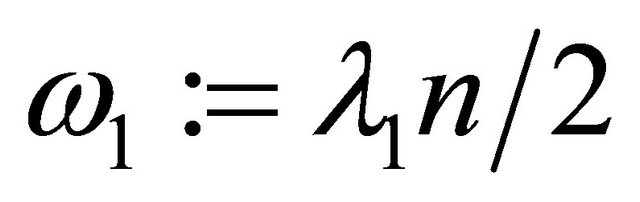 and
and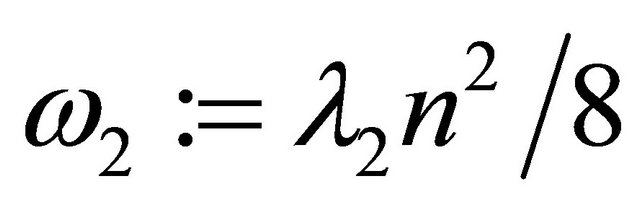 , we have
, we have
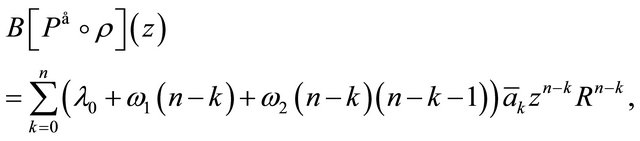
and in particular for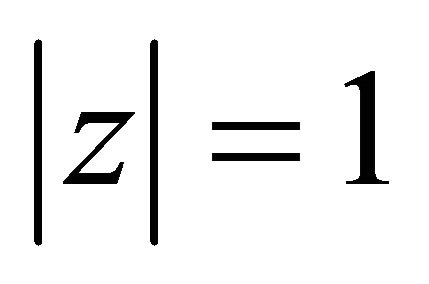 , we get
, we get
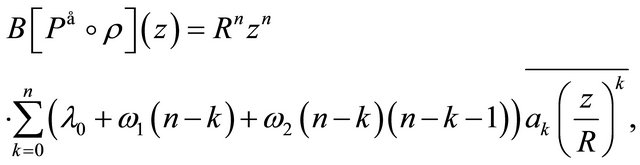
whence
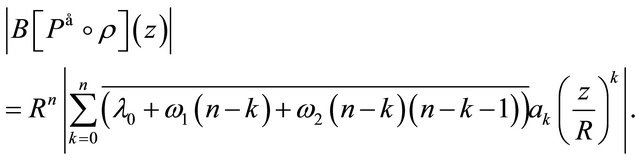
But
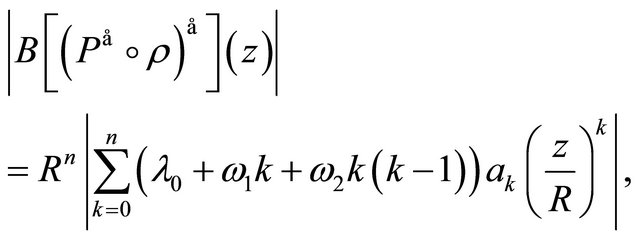
so the asserted identity does not hold in general for every 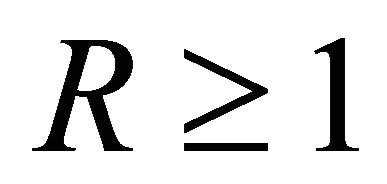 and
and 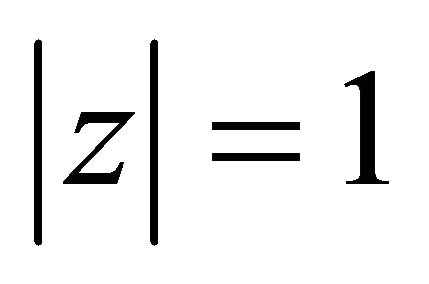 as e.g. the immediate counterexample of
as e.g. the immediate counterexample of 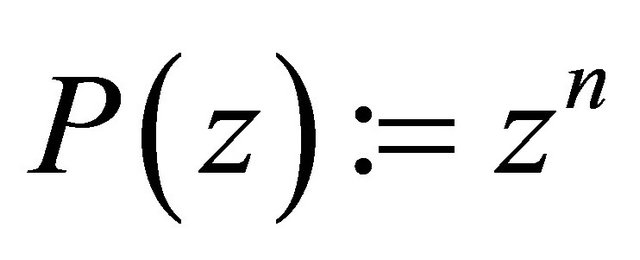 demonstrates in view of
demonstrates in view of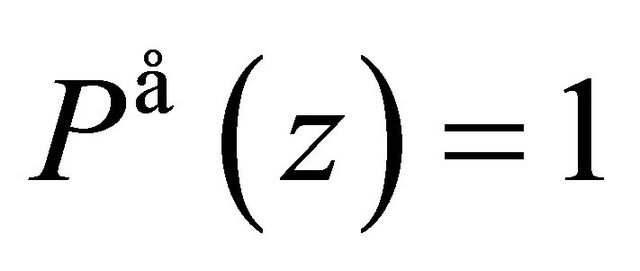 ,
,
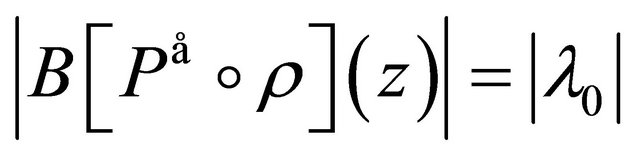 and
and
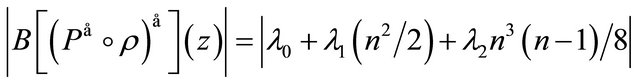
for 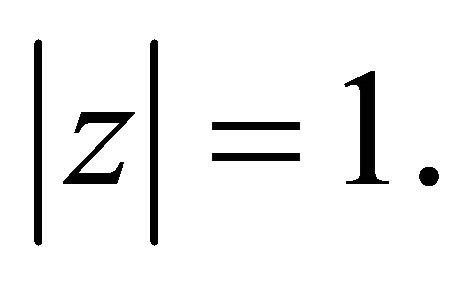
Authors [1] have also claimed that Inequality (1.17) and its analogue for self-inversive polynomials are sharp has remained to be verified. In fact, this claim is also wrong.
The main aim of this paper is to establish 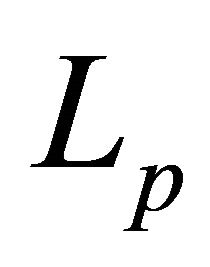 -mean extensions of the inequalities (1.14) and (1.15) for
-mean extensions of the inequalities (1.14) and (1.15) for 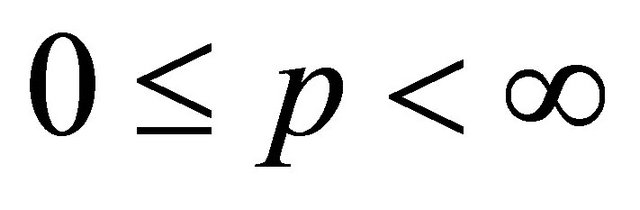 and present correct proofs of the results mentioned in [1]. In this direction, we first present the following result which is a compact generalization of the Inequalities (1.1), (1.2), (1.14) and (1.16) and also extend Inequality (1.17) for
and present correct proofs of the results mentioned in [1]. In this direction, we first present the following result which is a compact generalization of the Inequalities (1.1), (1.2), (1.14) and (1.16) and also extend Inequality (1.17) for 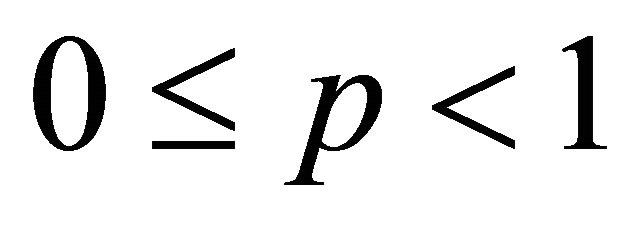 as well.
as well.
Theorem 1. If 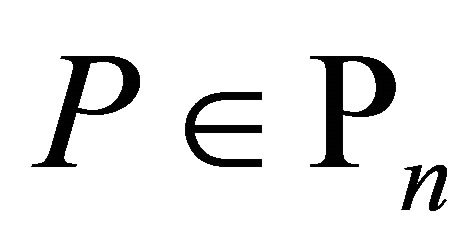 then for
then for 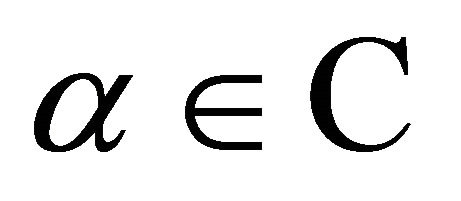 with
with 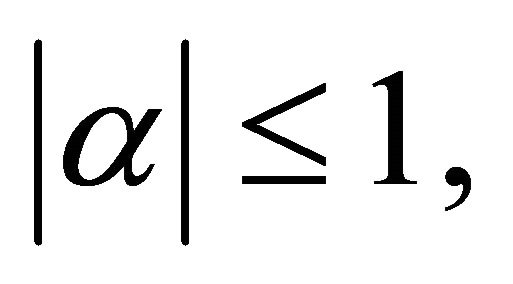
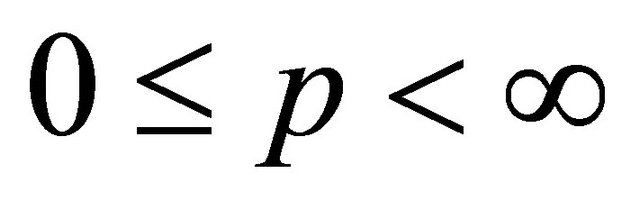 and
and 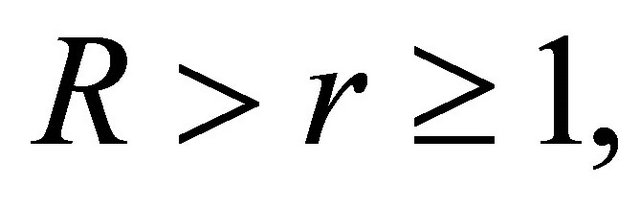
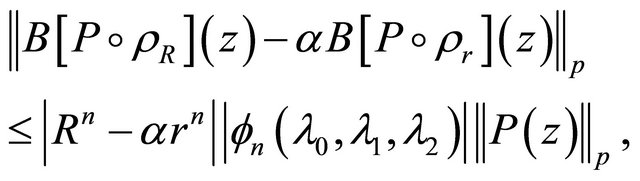 (1.18)
(1.18)
where 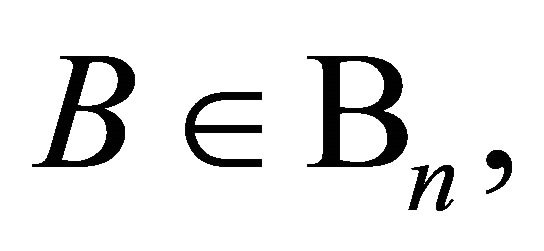
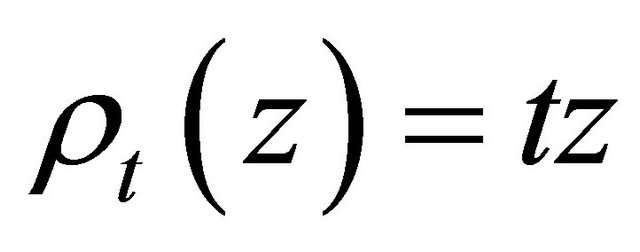 and
and 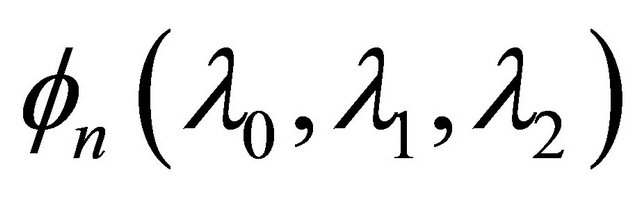 is given by (1.13). The result is best possible and equality holds in (1.18) for
is given by (1.13). The result is best possible and equality holds in (1.18) for 
If we choose 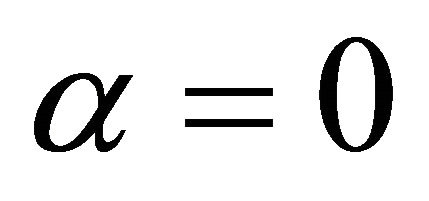 in (1.18), we get the following result which extends Theorem A to
in (1.18), we get the following result which extends Theorem A to 
Corollary 1. If 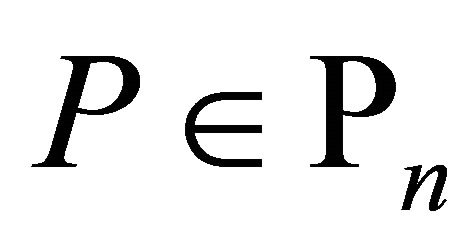 then for
then for 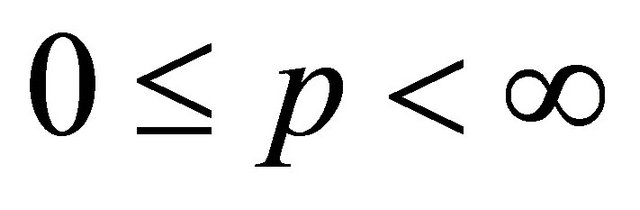 and
and 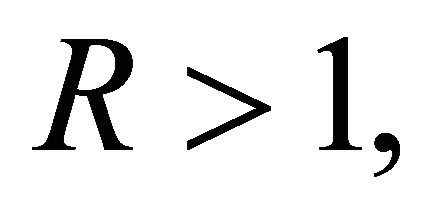
 (1.19)
(1.19)
where 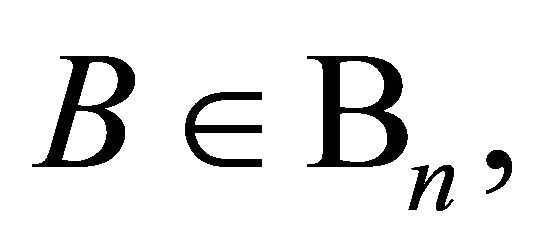
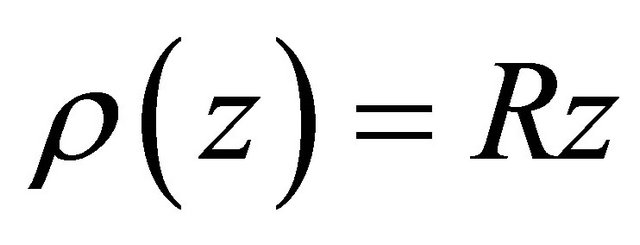 and
and 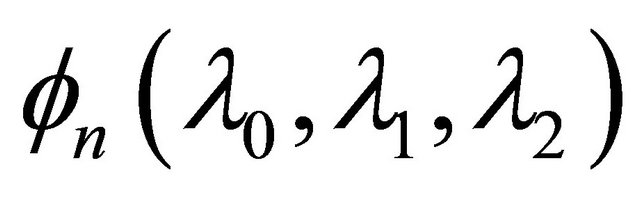 is given by (1.13).
is given by (1.13).
Remark 1. Taking 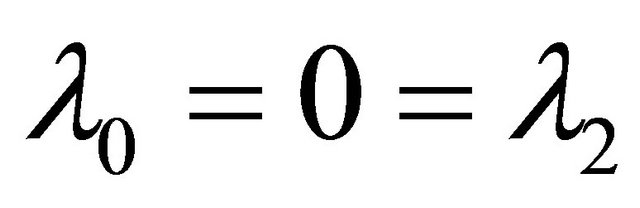 in (1.19) and noting that in this case all the zeros of U(z) defined in (1.10) lie in
in (1.19) and noting that in this case all the zeros of U(z) defined in (1.10) lie in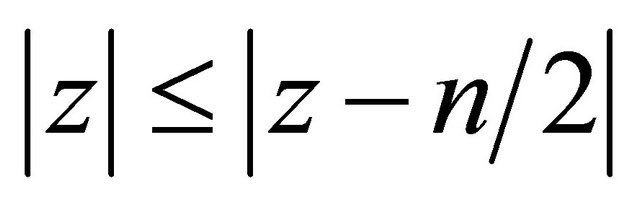 , we get for
, we get for 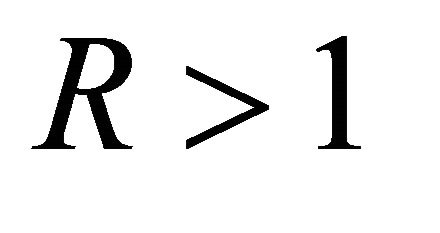 and
and 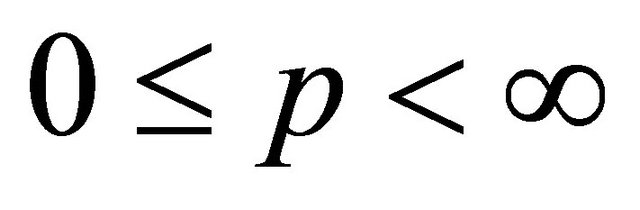
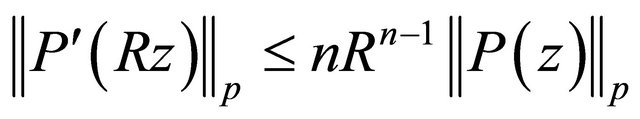 which includes (1.4) as a special case. Next if we choose
which includes (1.4) as a special case. Next if we choose  in (1.19), we get inequality (1.4). Inequality (1.11) also follows from Theorem 1 by letting
in (1.19), we get inequality (1.4). Inequality (1.11) also follows from Theorem 1 by letting  in (1.18).
in (1.18).
Theorem 1 can be sharpened if we restrict ourselves to the class of polynomials 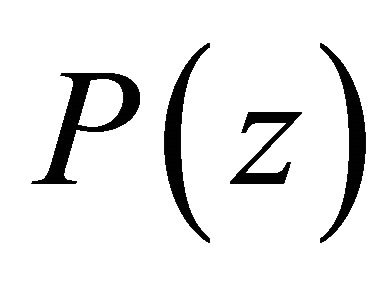 which does not vanish in
which does not vanish in 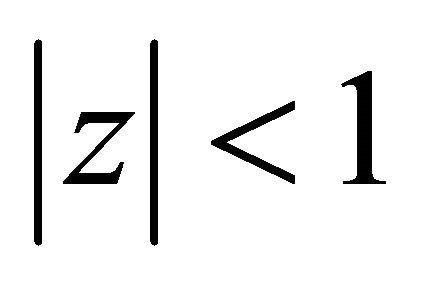 In this direction, we next present the following interesting compact generalization of Theorem B which yields
In this direction, we next present the following interesting compact generalization of Theorem B which yields 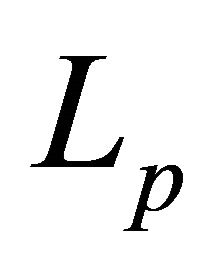 mean extension of the inequality (1.12) for
mean extension of the inequality (1.12) for  which among other things includes a correct proof of inequality (1.17) for
which among other things includes a correct proof of inequality (1.17) for 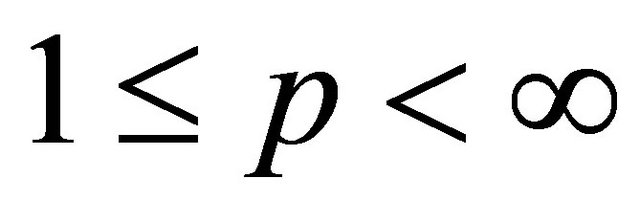 as a special case.
as a special case.
Theorem 2. If 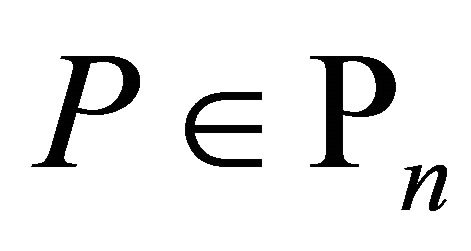 and
and  does not vanish for
does not vanish for 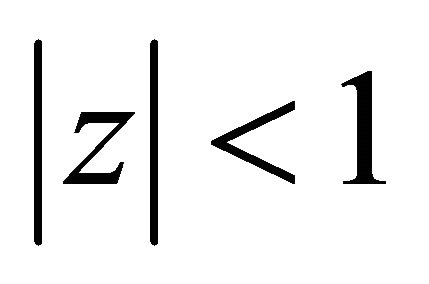 then for
then for  with
with 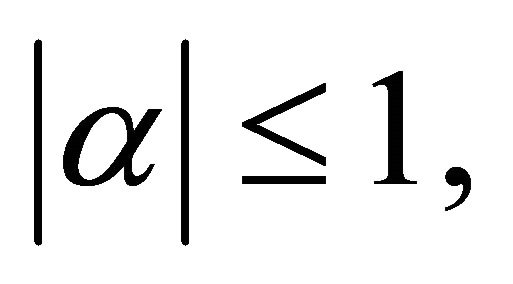
 and
and 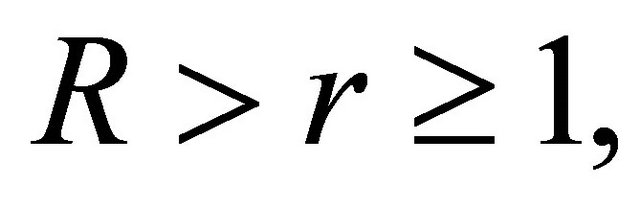
 (1.20)
(1.20)
where 
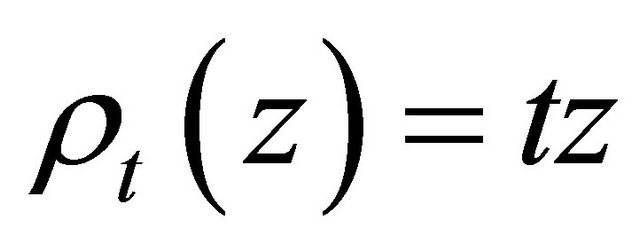 and
and 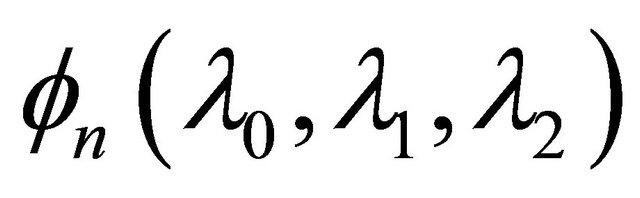 is defined by (1.13). The result is best possible and equality holds in (1.18) for
is defined by (1.13). The result is best possible and equality holds in (1.18) for 
 .
.
If we take 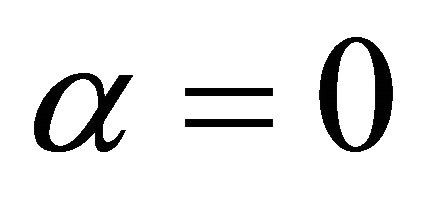 in (1.20), we get the following result which is the generalization of Theorem B for
in (1.20), we get the following result which is the generalization of Theorem B for  but also extends it for
but also extends it for 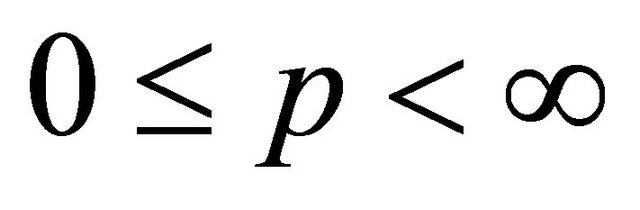
Corollary 2. If 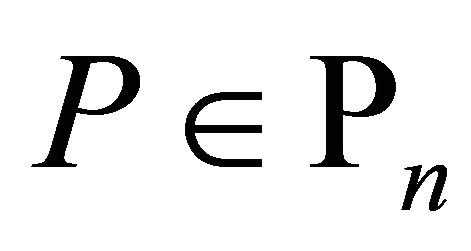 and
and 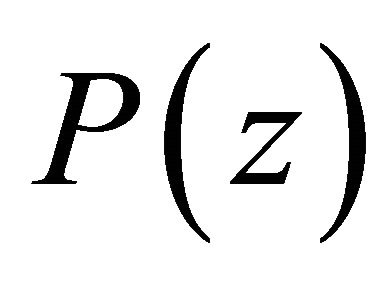 does not vanish for
does not vanish for 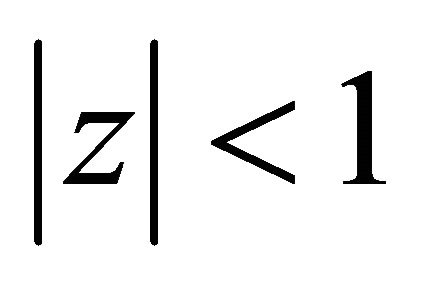 then for
then for 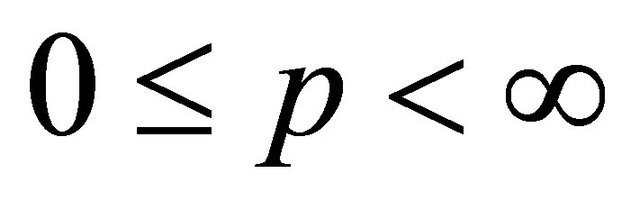 and
and 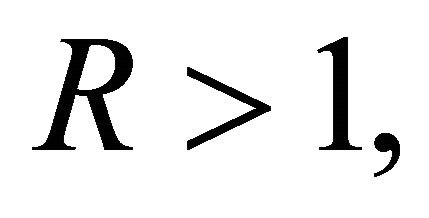
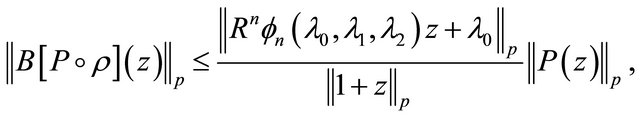
(1.21)
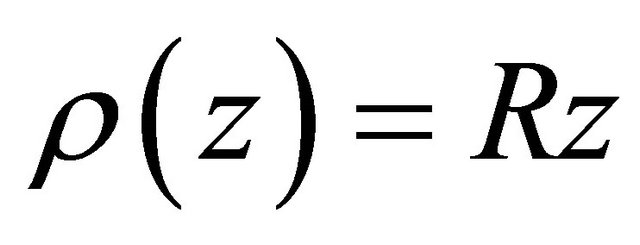
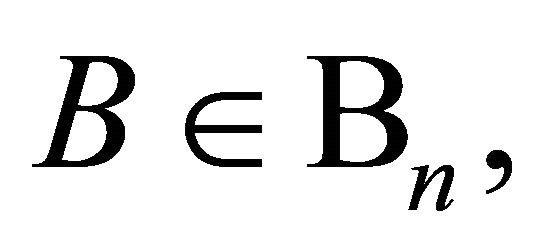 and
and 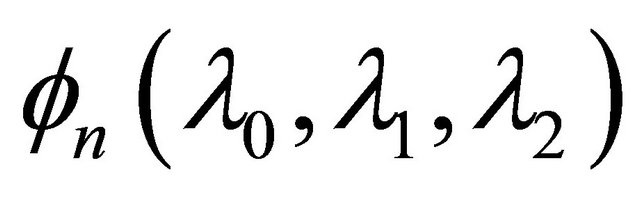 is defined by (1.13).
is defined by (1.13).
By triangle inequality, the following result is an immediately follows from Corollary 2.
Corollary 3. If 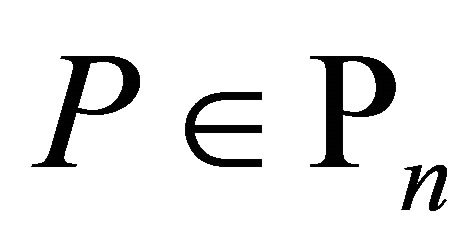 and
and 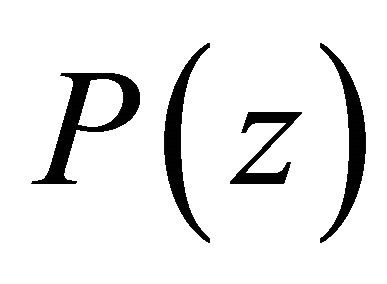 does not vanish for
does not vanish for 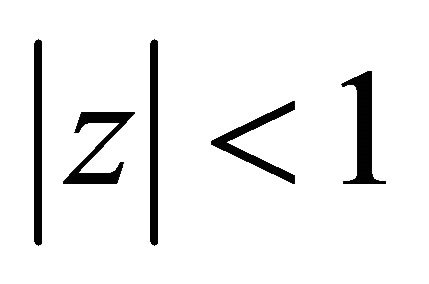 then for
then for 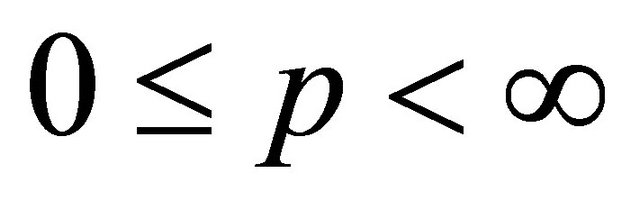 and
and 
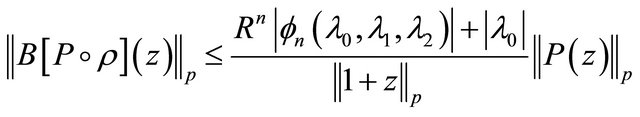 (1.22)
(1.22)
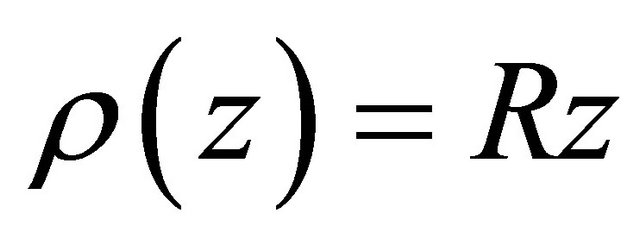
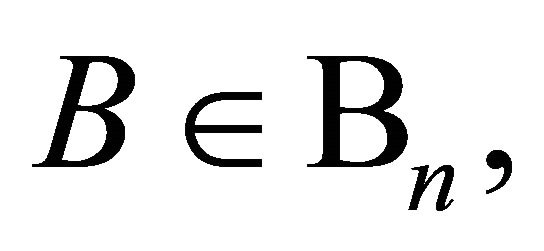 and
and 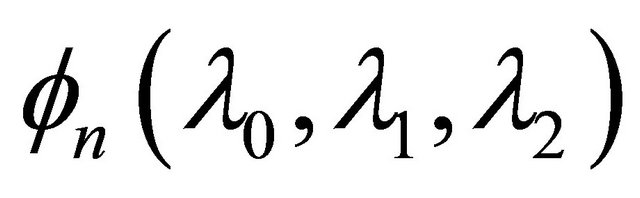 is defined by (1.13).
is defined by (1.13).
Remark 2. Corollary 3 establishes a correct proof of a result due to Shah and Liman [1, Theorem 3] for 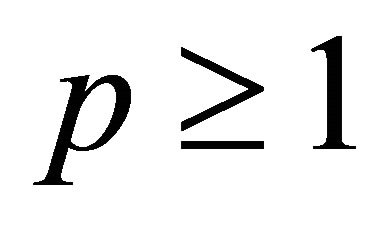 and also extends it for
and also extends it for 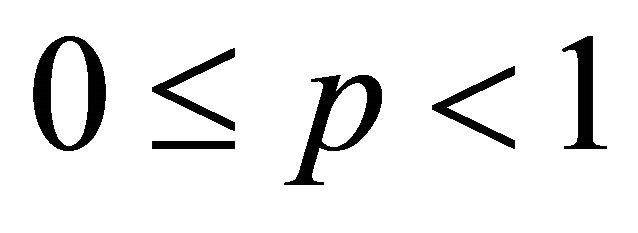 as well.
as well.
Remark 3. If we choose  in (1.21), we get for
in (1.21), we get for 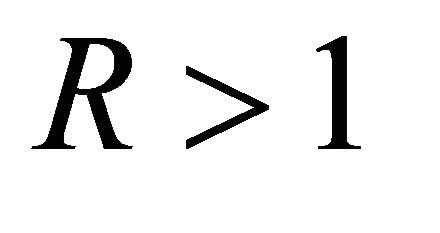 and
and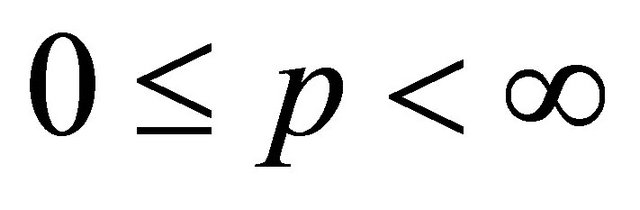 ,
,
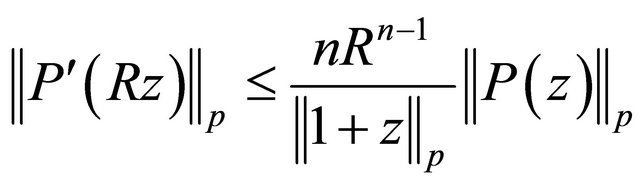
which, in particular, yields Inequality (1.7). Next if we take  in (1.21), we get Inequality (1.8). Inequality (1.12) can be obtained from corollary 2 by letting
in (1.21), we get Inequality (1.8). Inequality (1.12) can be obtained from corollary 2 by letting  in (1.20).
in (1.20).
By using triangle inequality, the following result immediately follows from Theorem 2.
Corollary 4. If 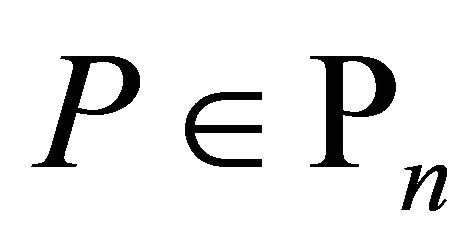 and
and 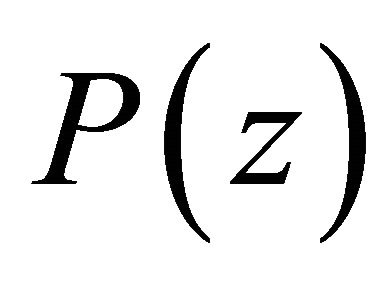 does not vanish for
does not vanish for 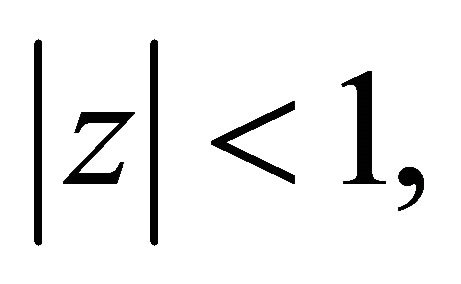 then for
then for  with
with 
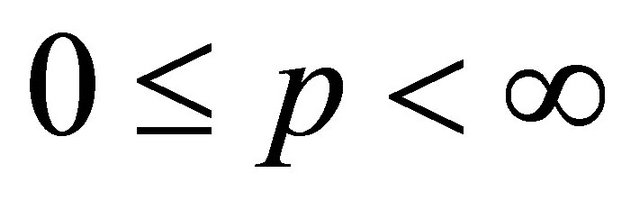 and
and 
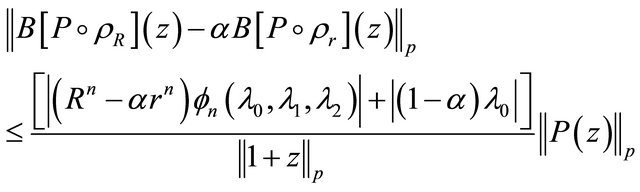 (1.23)
(1.23)
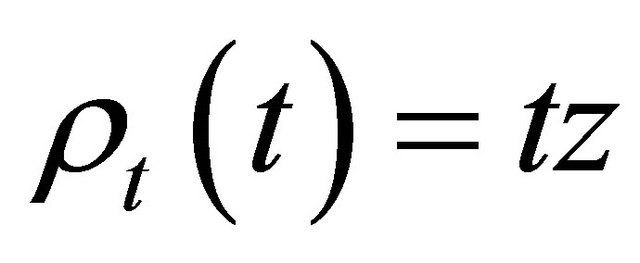
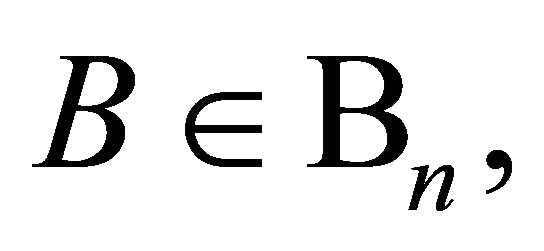 and
and 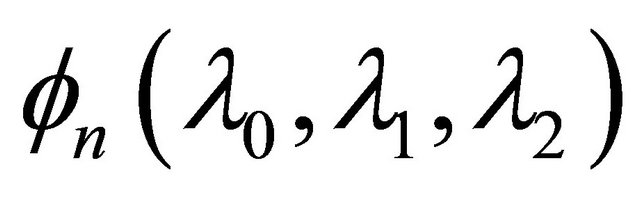 is defined by (1.13).
is defined by (1.13).
A polynomial  is said be self-inversive if
is said be self-inversive if 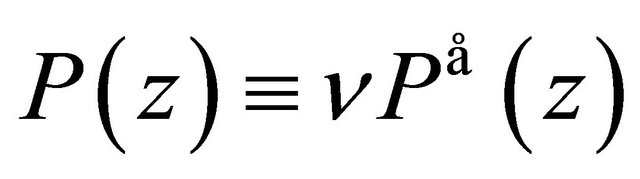 where
where 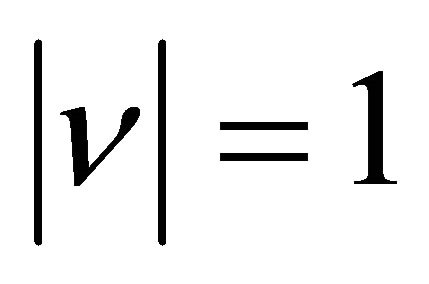 and
and 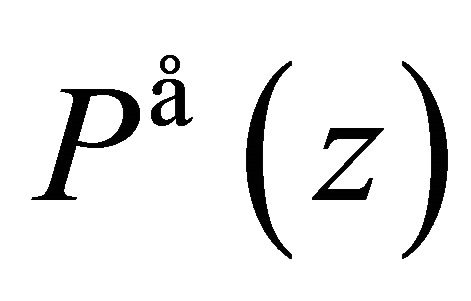 is the conjugate polynomial of
is the conjugate polynomial of , that is,
, that is,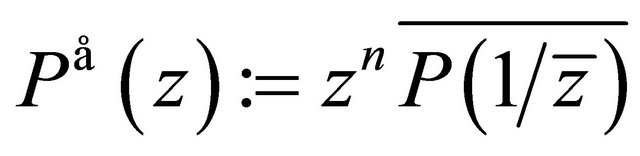 .
.
Finally in this paper, we establish the following result for self-inversive polynomials , which includes a correct proof of an another result of Shah and Liman [1, Theorem 2] as a special case.
Theorem 3. If 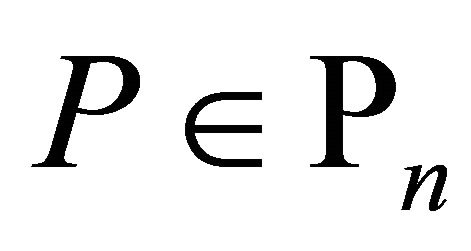 and
and 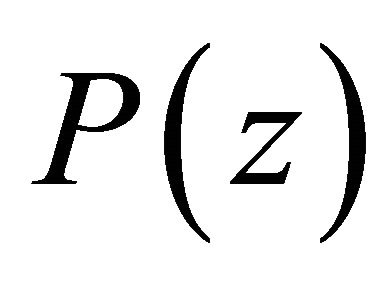 is a self-inversive polynomial, then for
is a self-inversive polynomial, then for 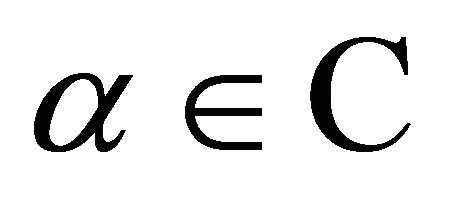 with
with 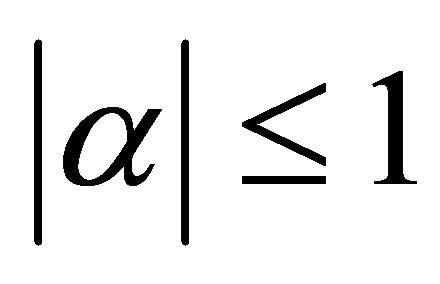
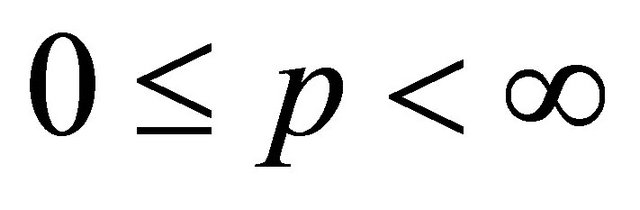 and
and 
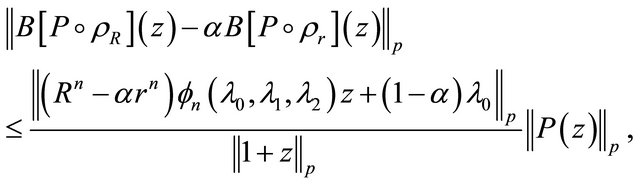 (1.24)
(1.24)
where 
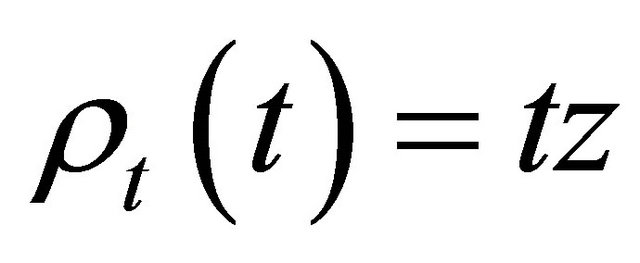 and
and 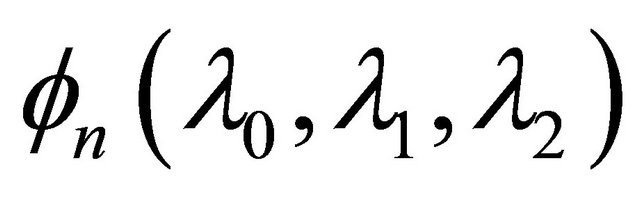 is given by (1.13). The result is sharp and an extremal polynomial is
is given by (1.13). The result is sharp and an extremal polynomial is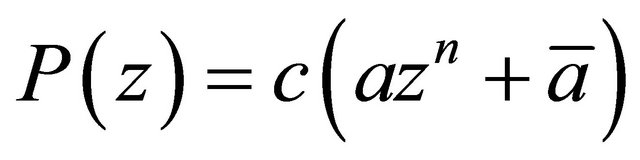 ,
,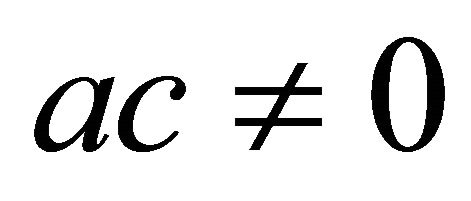 .
.
For 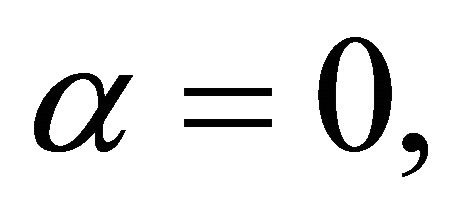 we get the following result.
we get the following result.
Corollary 5. If 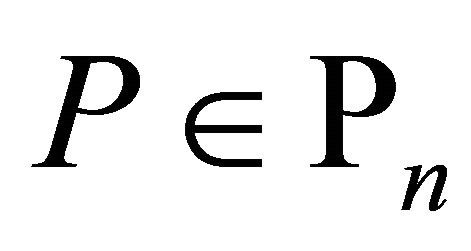 and
and 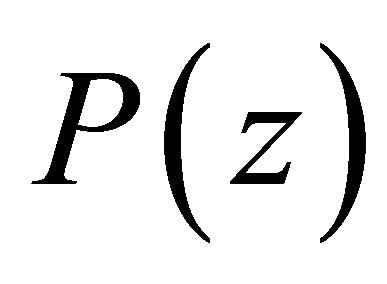 is a self-inversive polynomial, then for
is a self-inversive polynomial, then for 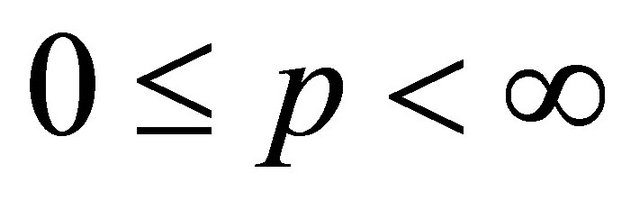 and
and 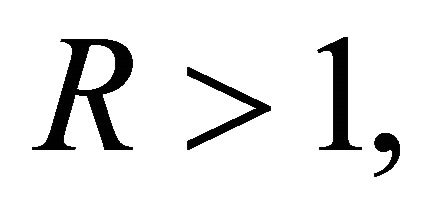
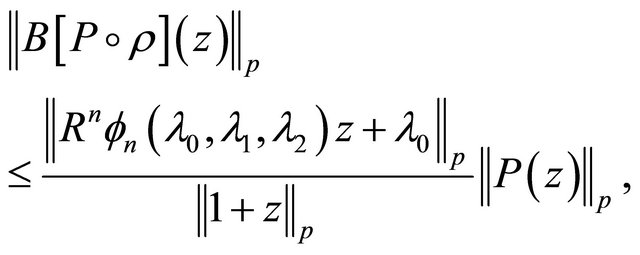 (1.25)
(1.25)
where 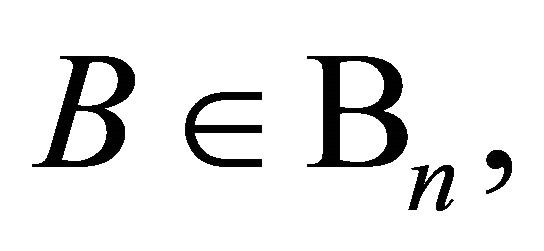
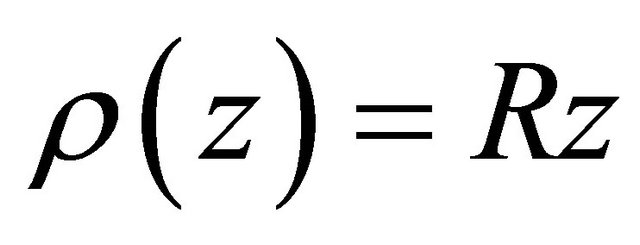 and
and 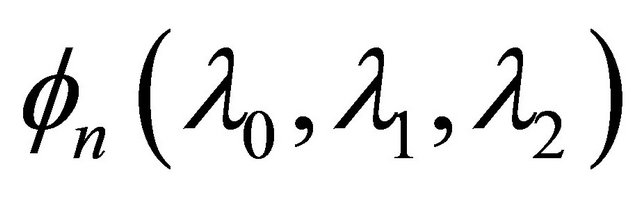 is given by (1.13).
is given by (1.13).
The following result is an immediate consequence of Corollary 5.
Corollary 6 If 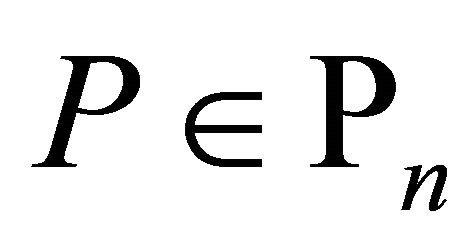 and
and 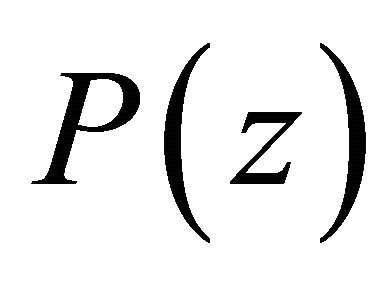 is a self-inversive polynomial, then for
is a self-inversive polynomial, then for 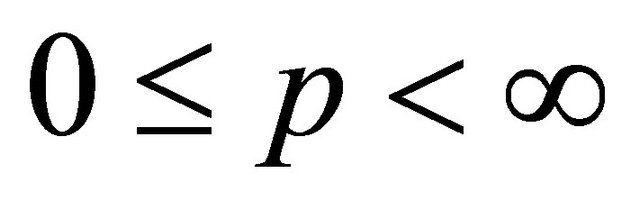 and
and 
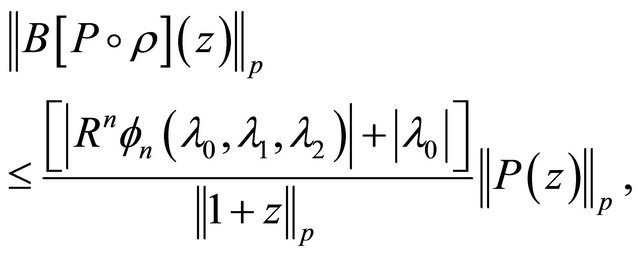 (1.26)
(1.26)
where 
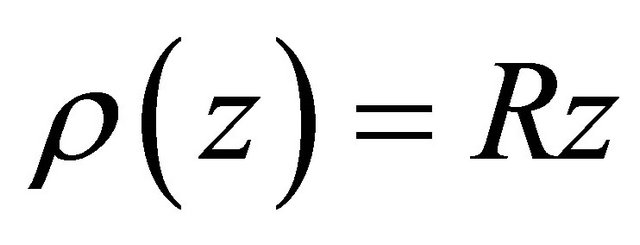 and
and 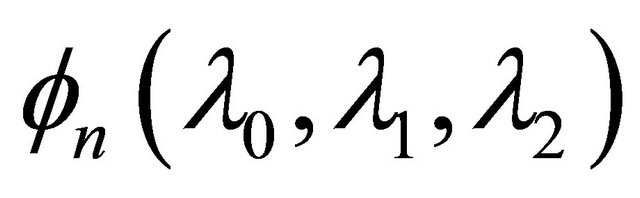 is given by (1.13).
is given by (1.13).
Remark 4. Corollary 6 establishes a correct proof of a result due to Shah and Liman [1, Theorem 3] for 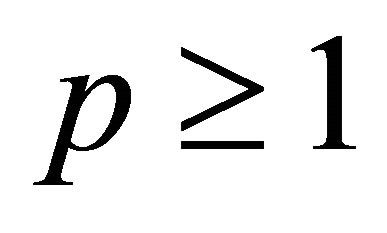 and also extends it for
and also extends it for 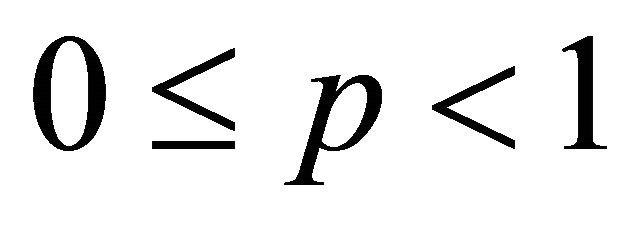 as well.
as well.
Remark 5. A variety of interesting results can be easily deduced from Theorem 3 in the same way as we have deduced from Theorem 2. Here we mention a few of these. Taking 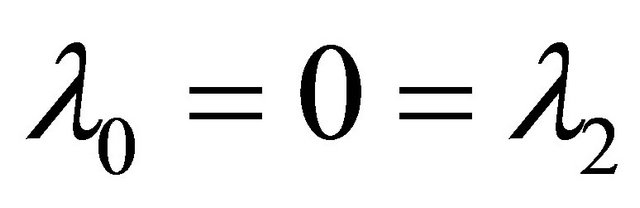 = in (1.25), we get for
= in (1.25), we get for 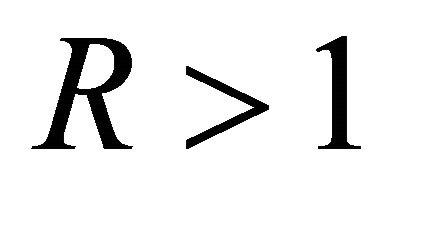 and
and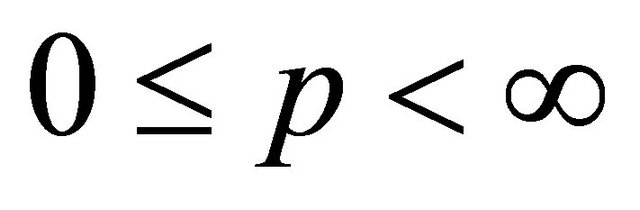 ,
,
 which, in particular, yields a result due to Dewan and Govil [17] and A. Aziz [18] for polynomials
which, in particular, yields a result due to Dewan and Govil [17] and A. Aziz [18] for polynomials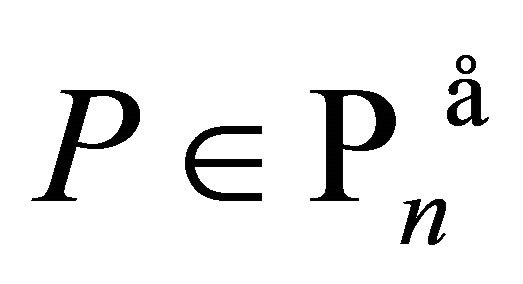 . Next if we choose
. Next if we choose 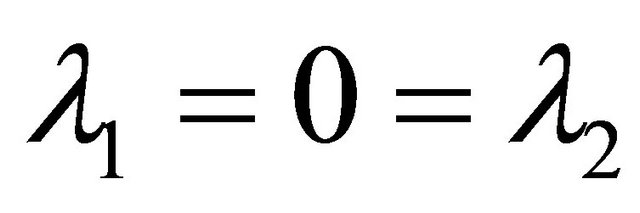 in (1.25), we get for
in (1.25), we get for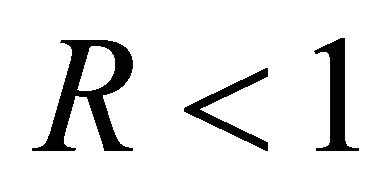 ;
; 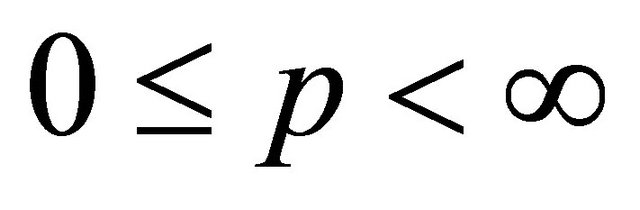
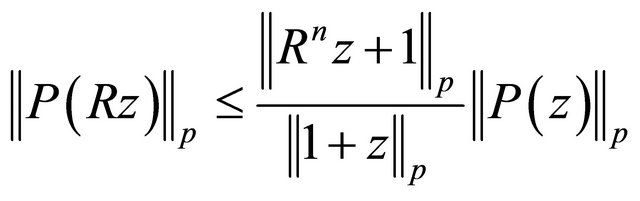 .
.
The above inequality is a special case of a result proved by Aziz and Rather [19].
Lastly letting  in (1.25), it follows that if
in (1.25), it follows that if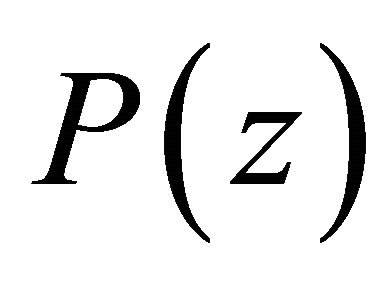 , is a self-inversive polynomial then
, is a self-inversive polynomial then
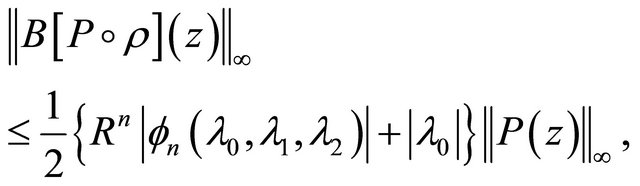 (1.27)
(1.27)
where ,
, 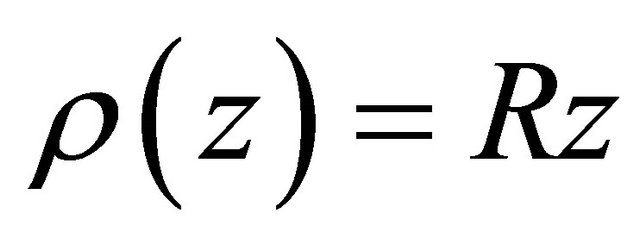 and
and 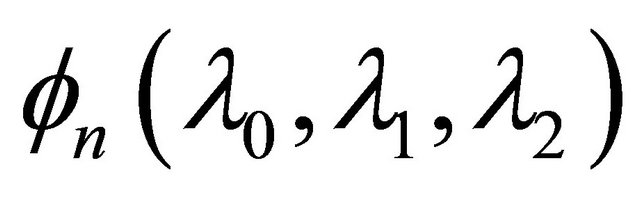 is defined by (1.13). The result is sharp.
is defined by (1.13). The result is sharp.
Inequality (1.27) is a special case of a result due to Rahman and Schmeisser [4, Cor. 14.5.6].
2. Lemma
For the proof of above theorems we need the following Lemmas:
The following lemma follows from Corollary 18.3 of [20, p. 86].
Lemma 1. If 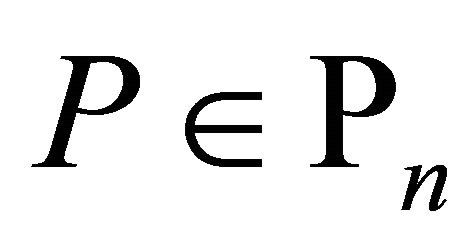 and
and 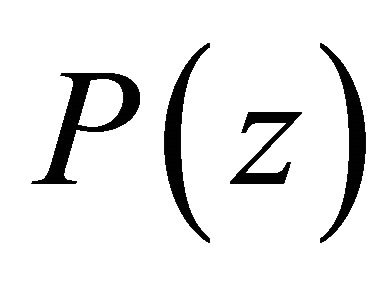 has all zeros in
has all zeros in 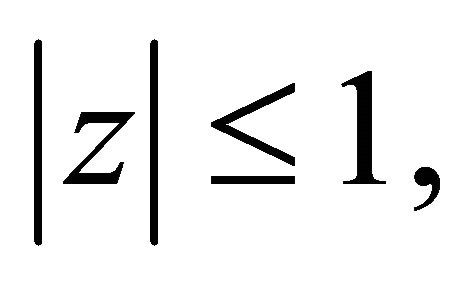 then all the zeros of
then all the zeros of  also lie in
also lie in 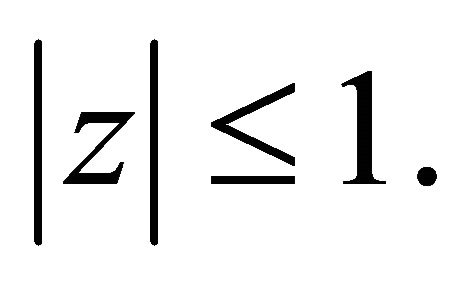
Lemma 2. If 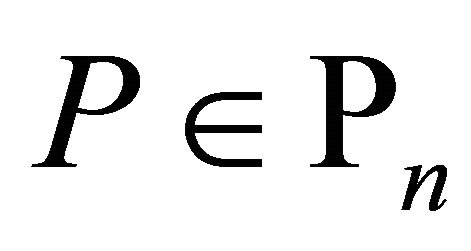 and
and  have all its zeros in
have all its zeros in  then for every
then for every 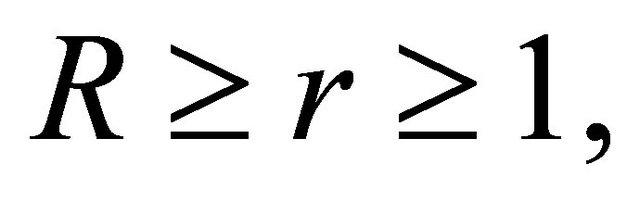 and
and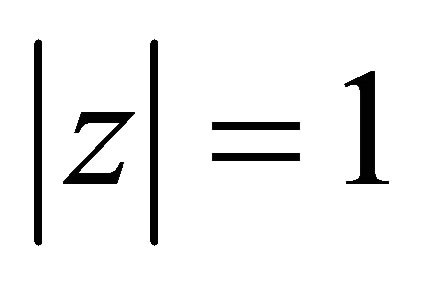 ,
,
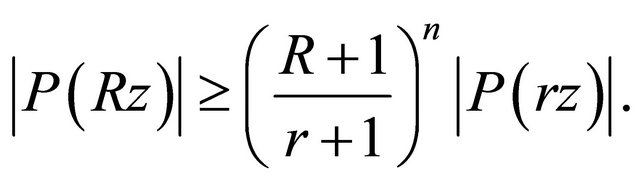
Proof. Since all the zeros of  lie in
lie in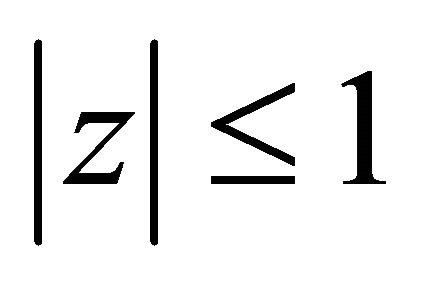 , we write
, we write
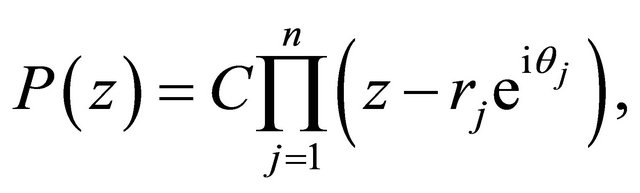
where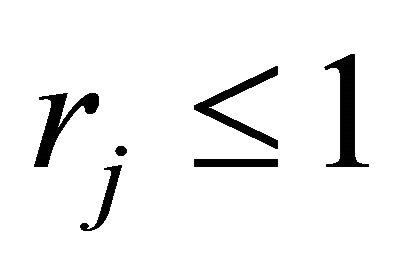 . Now for
. Now for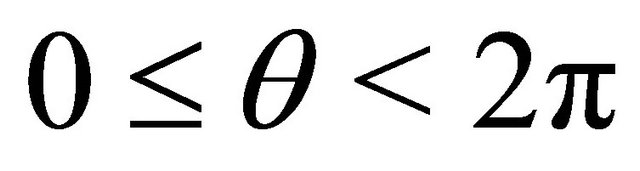 ,
, 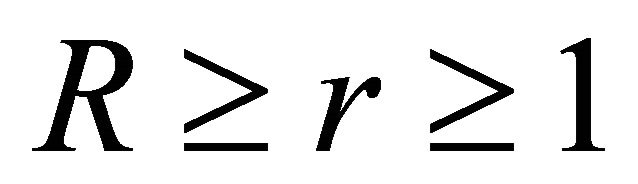 , we have
, we have
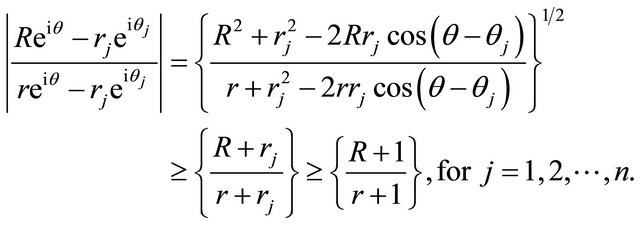
Hence
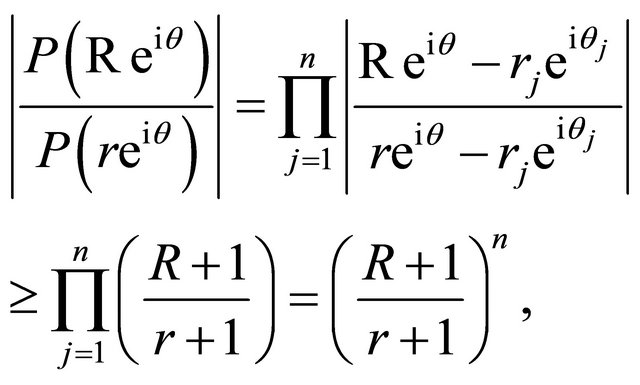
for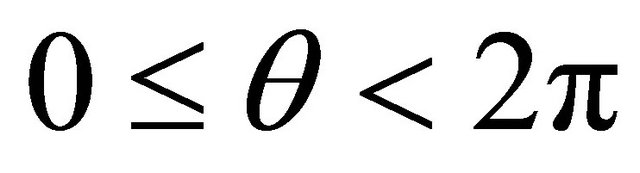 . This implies for
. This implies for 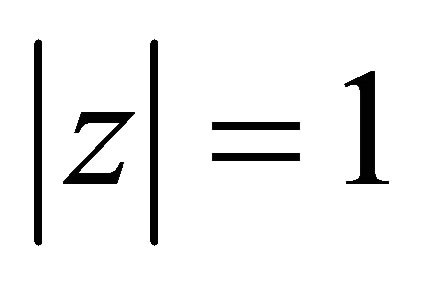 and
and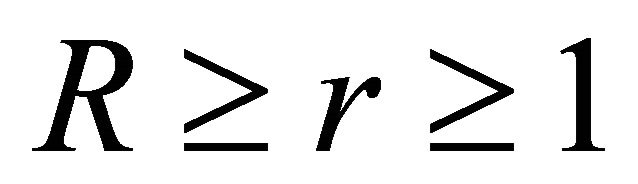 ,
,
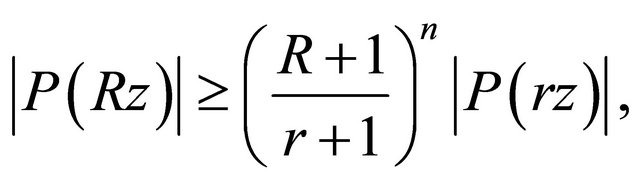
which completes the proof of Lemma 2.
Lemma 3. If 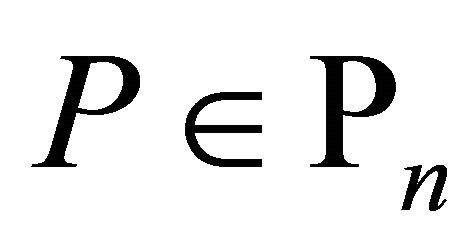 and
and 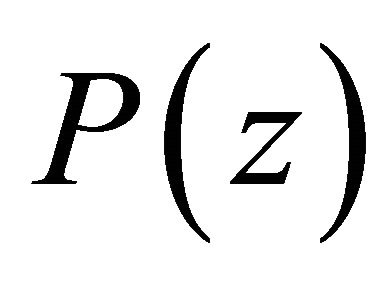 has no zero in
has no zero in 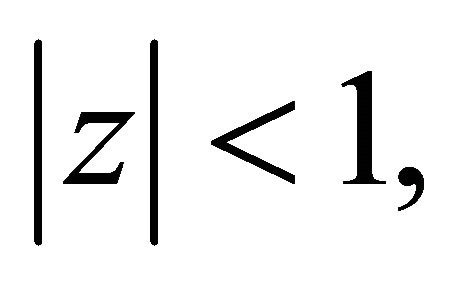 then for every
then for every  with
with 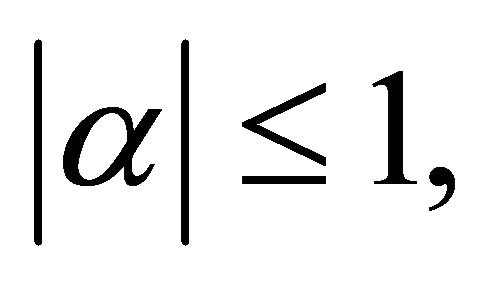
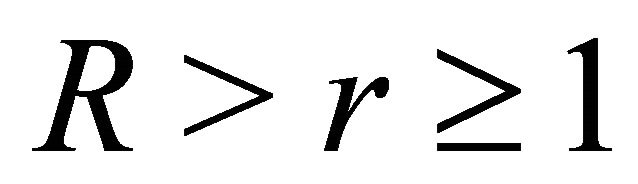 and
and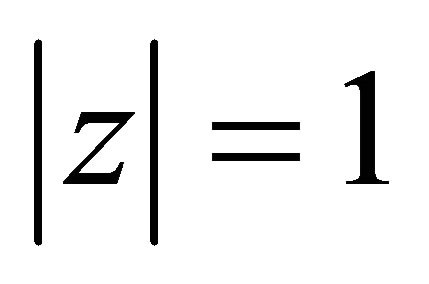 ,
,
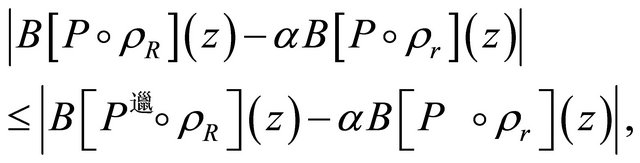 (2.1)
(2.1)
where 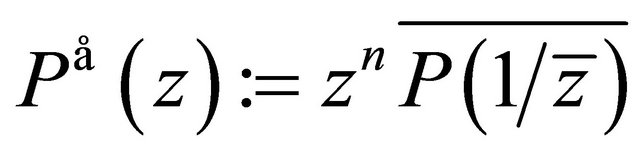 and
and 
Proof. Since the polynomial  has all its zeros in
has all its zeros in 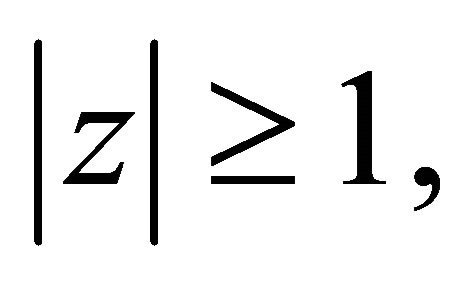 therefore, for every real or complex number
therefore, for every real or complex number ![]() with
with 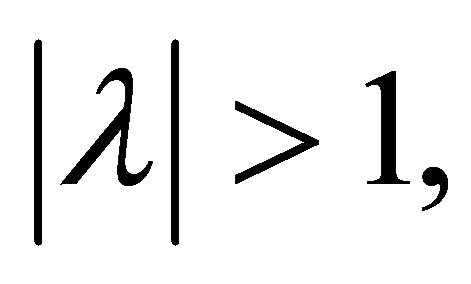 the polynomial
the polynomial 
where  has all zeros in
has all zeros in 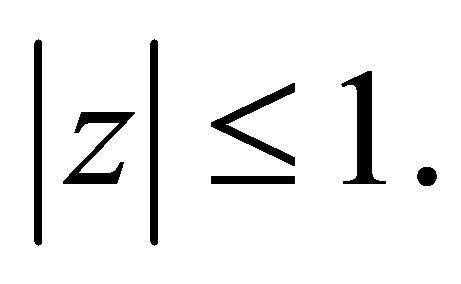 Applying Lemma 2 to the polynomial
Applying Lemma 2 to the polynomial 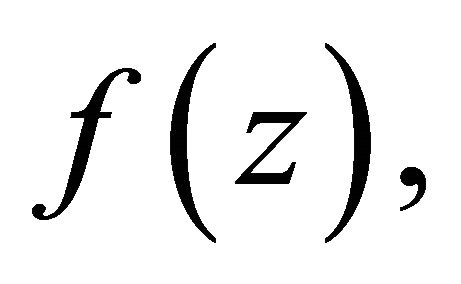 we obtain for every
we obtain for every 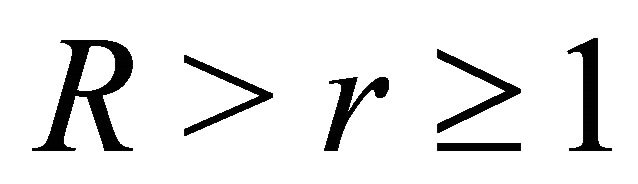 and
and 
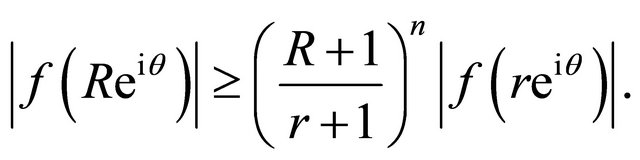 (2.2)
(2.2)
Since  for every
for every 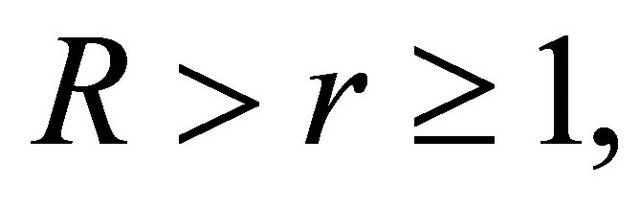
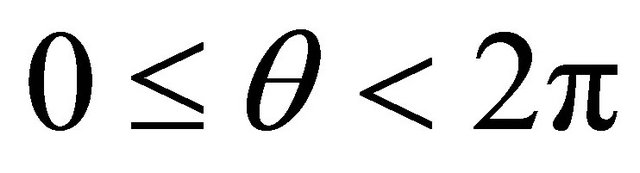 and
and  it follows from (2.2) that
it follows from (2.2) that

for every 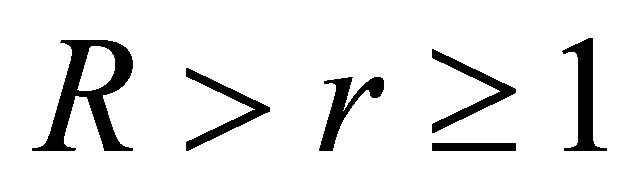 and
and 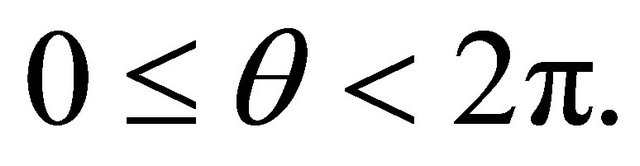 This gives
This gives
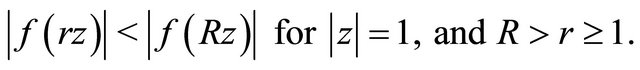
Using Rouche’s theorem and noting that all the zeros of 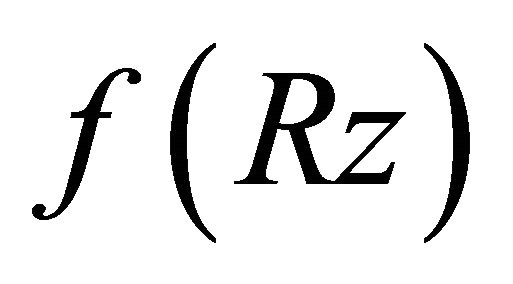 lie in
lie in 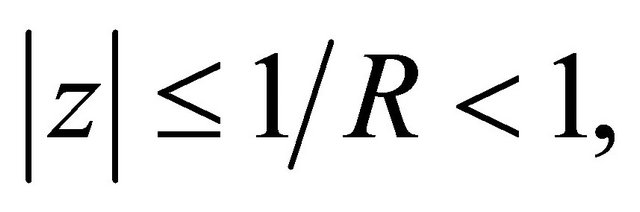 we conclude that the polynomial
we conclude that the polynomial
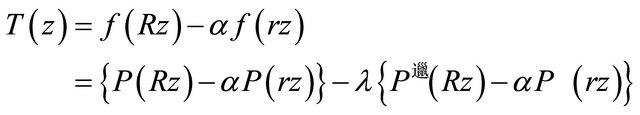
has all its zeros in 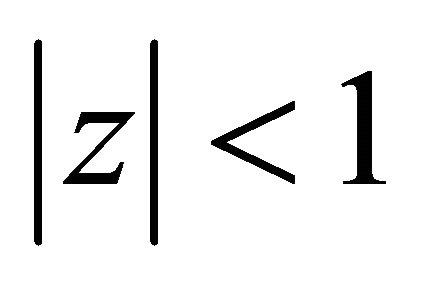 for every real or complex
for every real or complex ![]() with
with 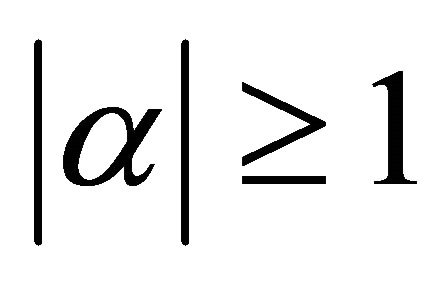 and
and 
Applying Lemma 1 to polynomial 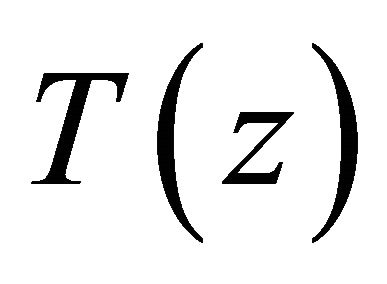 and noting that
and noting that 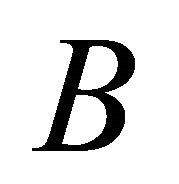 is a linear operator, it follows that all the zeros of polynomial
is a linear operator, it follows that all the zeros of polynomial
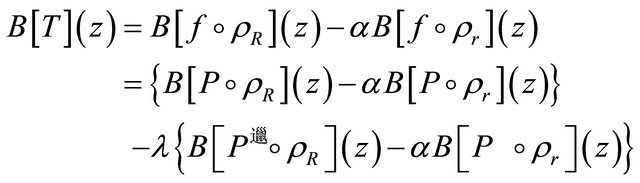
lie in 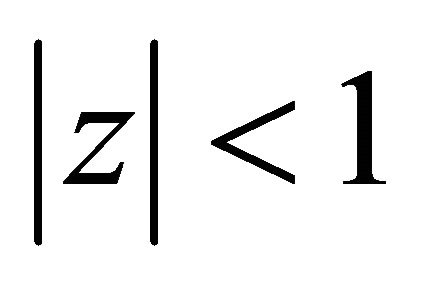 where
where  This implies
This implies
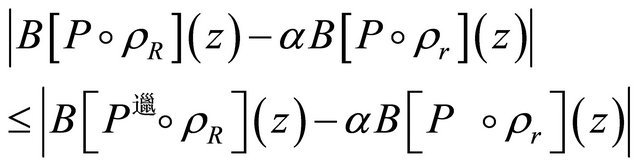 (2.3)
(2.3)
for 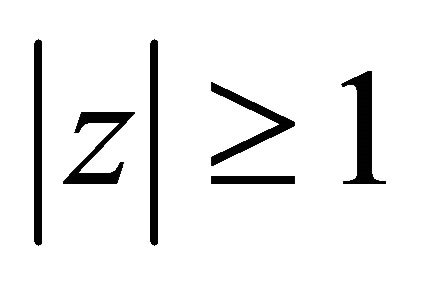 and
and 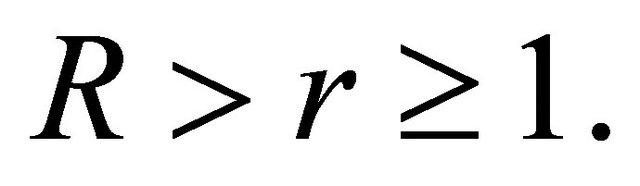 If Inequality (2.3) is not true, then there exits a point
If Inequality (2.3) is not true, then there exits a point 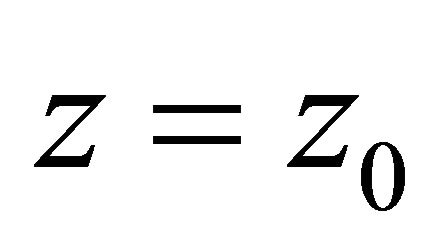 with
with  such that
such that
 (2.4)
(2.4)
But all the zeros of  lie in
lie in 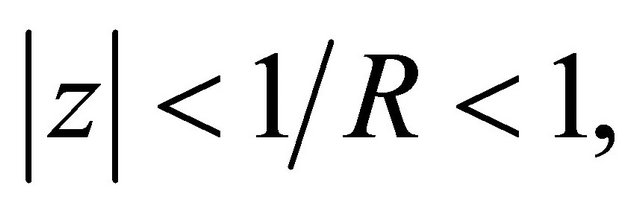 therefore, it follows (as in case of
therefore, it follows (as in case of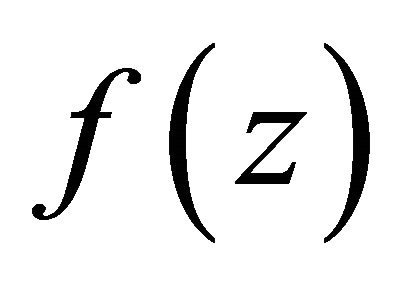 ) that all the zeros of
) that all the zeros of 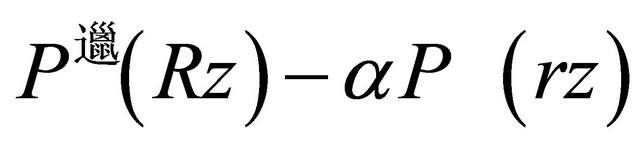 lie in
lie in 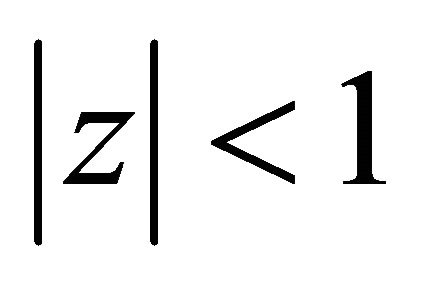 Hence, by Lemma 1, we have
Hence, by Lemma 1, we have

We take
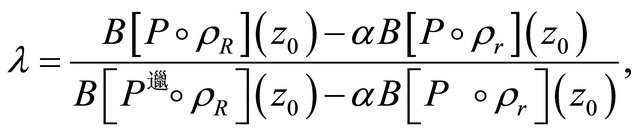
then ![]() is well defined real or complex number with
is well defined real or complex number with 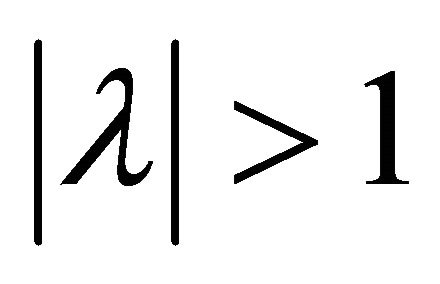 and with this choice of
and with this choice of 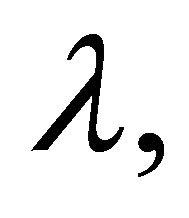 we obtain
we obtain 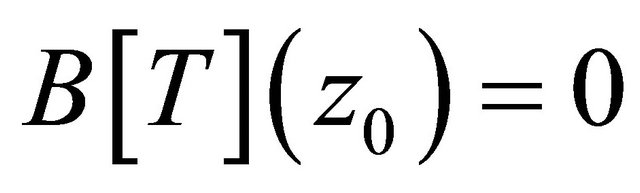 where
where  This contradicts the fact that all the zeros of
This contradicts the fact that all the zeros of 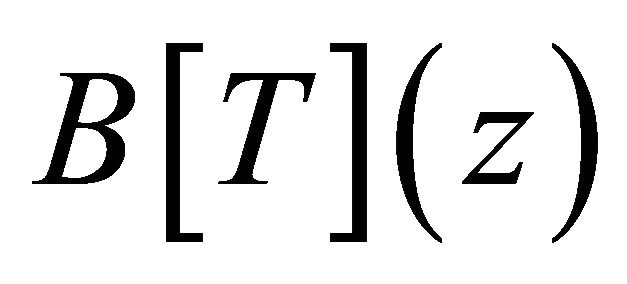 lie in
lie in  Thus (2.3) holds true for
Thus (2.3) holds true for 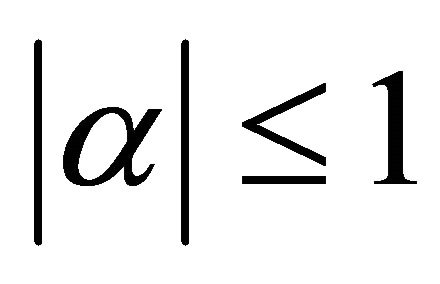 and
and 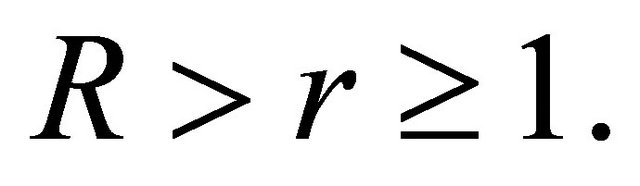
Next we describe a result of Arestov [11].
For  and
and
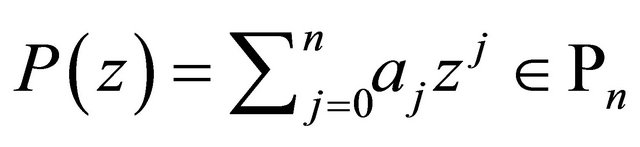 , we define
, we define
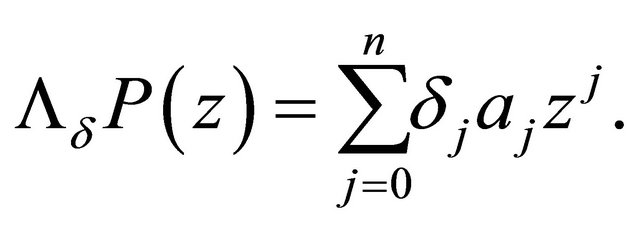
The operator  is said to be admissible if it preserves one of the following properties:
is said to be admissible if it preserves one of the following properties:
1) 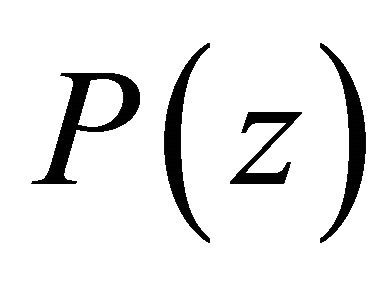 has all its zeros in
has all its zeros in 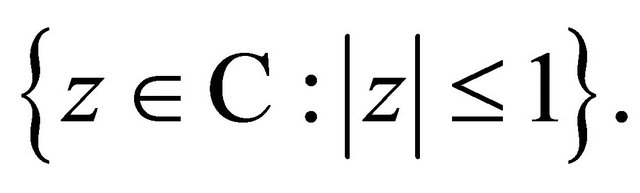
2) 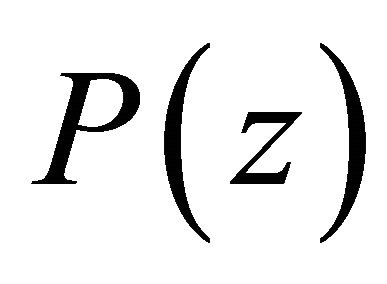 has all its zeros in
has all its zeros in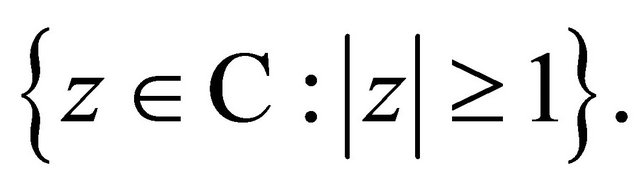
The result of Arestov [11] may now be stated as follows.
Lemma 4. [11, Theorem 4] Let 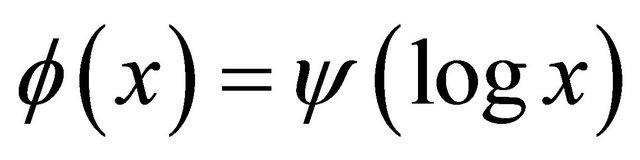 where
where  is a convex non decreasing function on
is a convex non decreasing function on 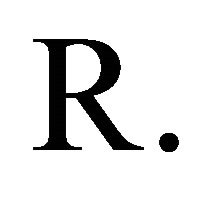 Then for all
Then for all 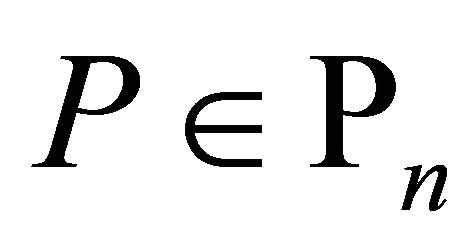 and each admissible operator
and each admissible operator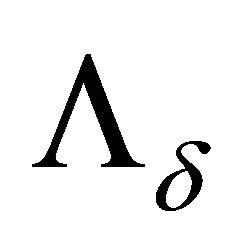 ,
,
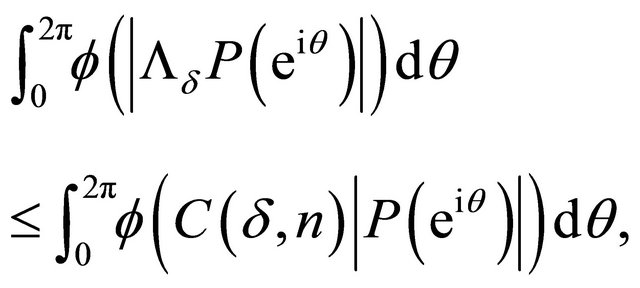
where 
In particular, Lemma 4 applies with 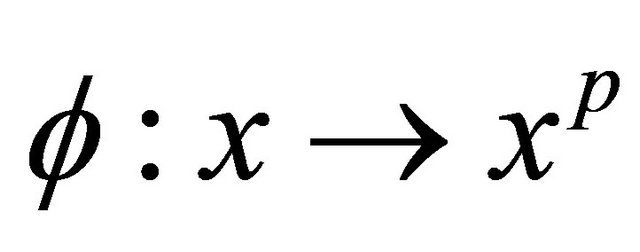 for every
for every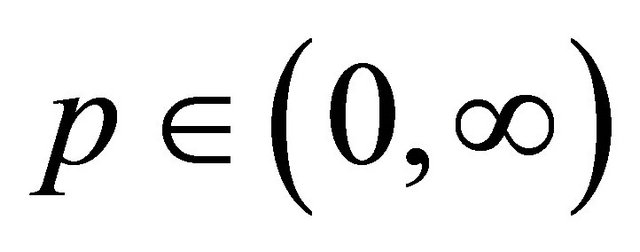 . Therefore, we have
. Therefore, we have
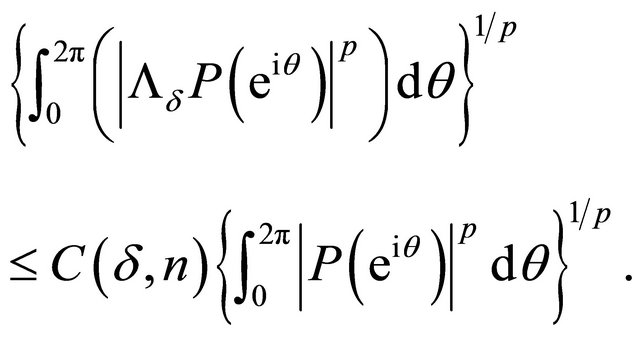 (2.5)
(2.5)
We use (2.5) to prove the following interesting result.
Lemma 5. If 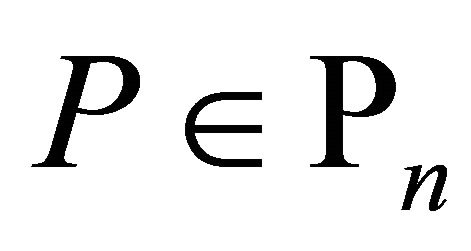 and
and 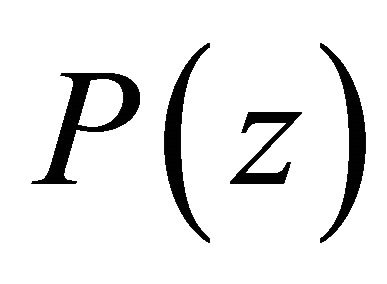 does not vanish in
does not vanish in 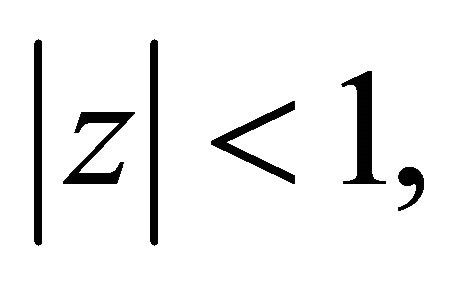 then for every
then for every ,
,  and for
and for ![]() real,
real,  ,
,
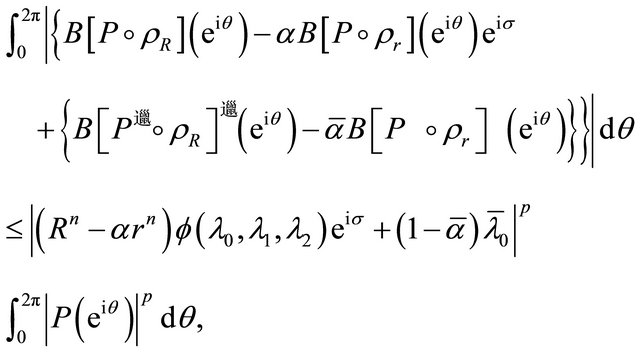 (2.6)
(2.6)
where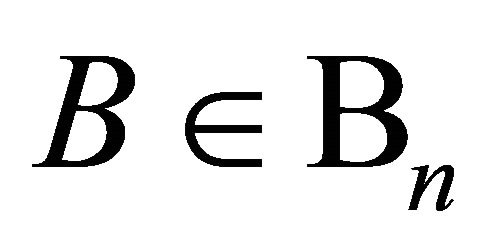 ,
, 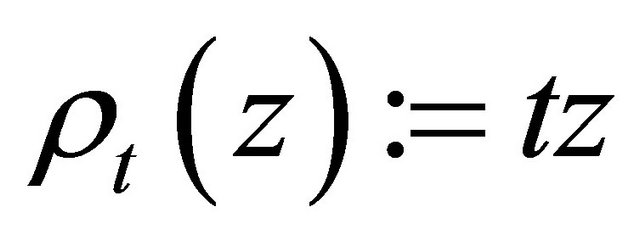 ,
,
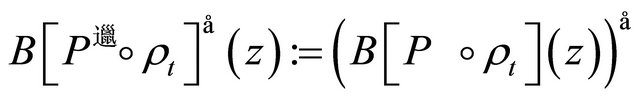 and
and 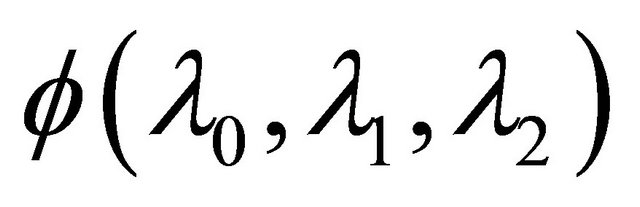
is defined by (1.13).
Proof. Since 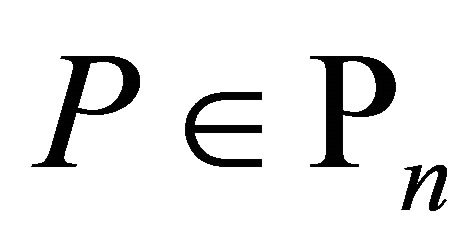 and
and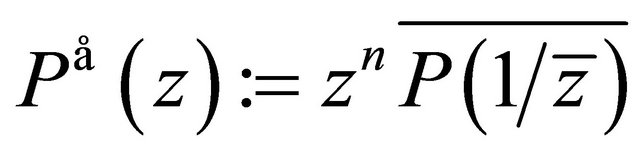 , by Lemma 3, we have for
, by Lemma 3, we have for 
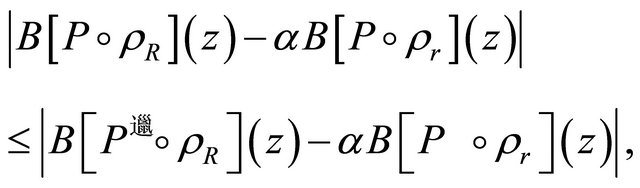 (2.7)
(2.7)
Also, since

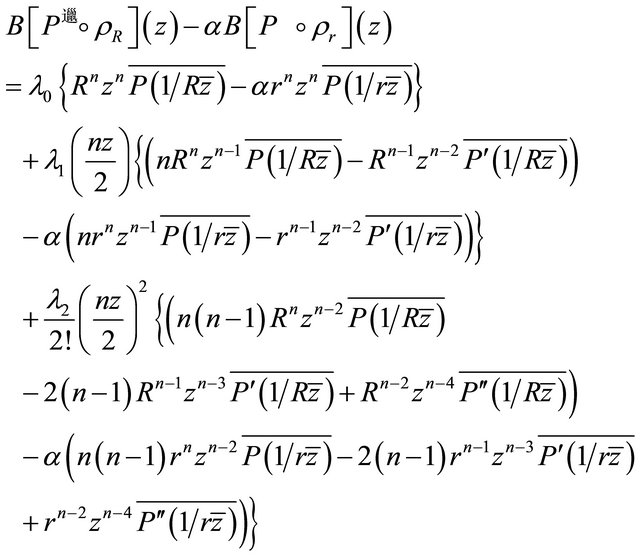
and therefore,
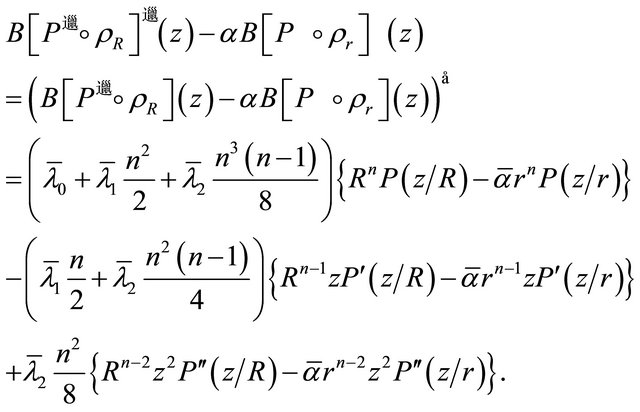
(2.8)
Also, for 
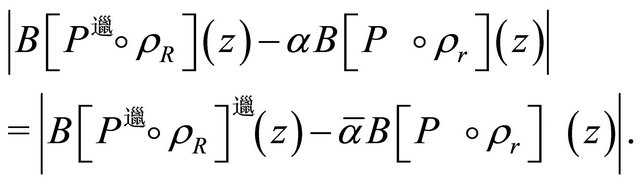
Using this in (2.7), we get for 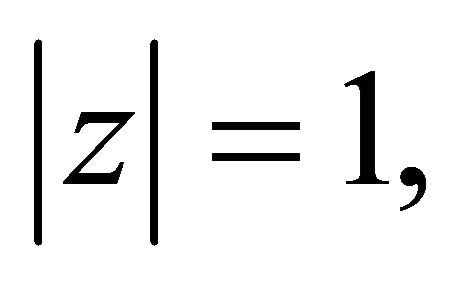
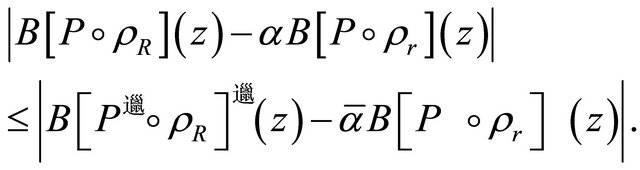
As in the proof of Lemma 3, the polynomial
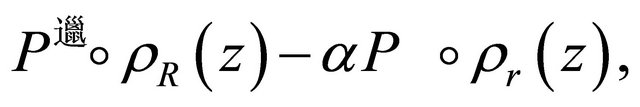 has all its zeros in
has all its zeros in 
and by Lemma 1, 
also has all its zero in 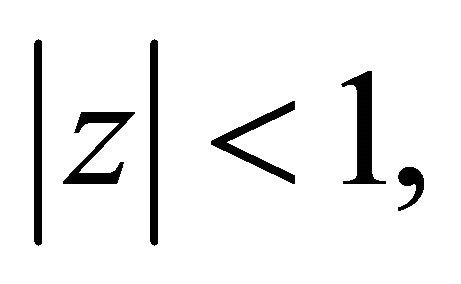 therefore,
therefore,
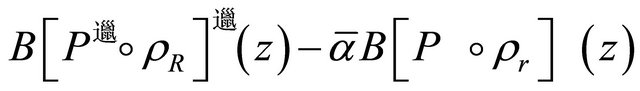 has all its zeros in
has all its zeros in
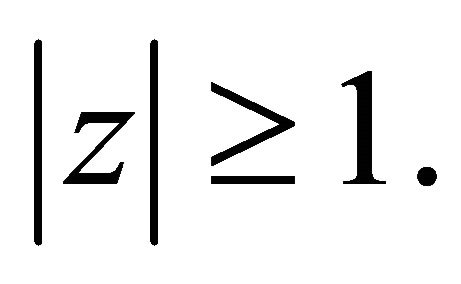 Hence by the maximum modulus principle, for
Hence by the maximum modulus principle, for 
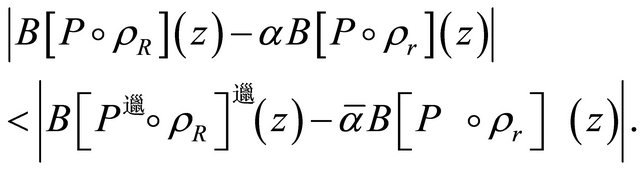 (2.9)
(2.9)
A direct application of Rouche’s theorem shows that with 
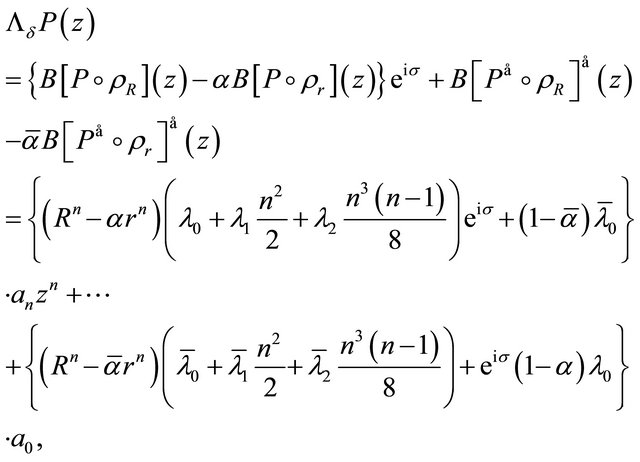
has all its zeros in 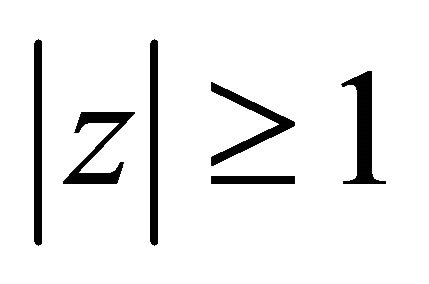 for every real
for every real 
 Therefore,
Therefore, 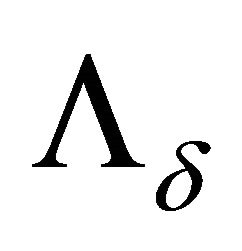 is an admissible operator. Applying (2.5) of Lemma 4, the desired result follows immediately for each
is an admissible operator. Applying (2.5) of Lemma 4, the desired result follows immediately for each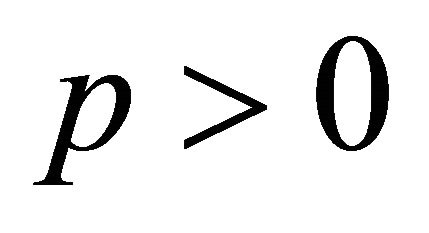 .
.
From Lemma 5, we deduce the following more general result.
Lemma 6. If 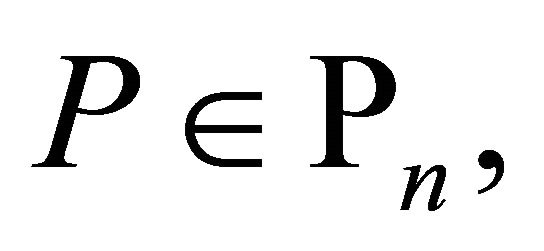 then for every
then for every 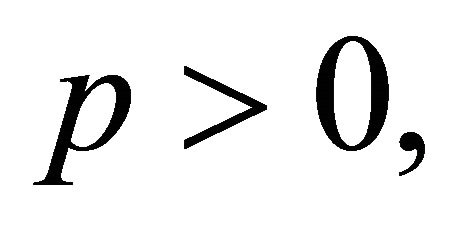
 and
and ![]() real
real 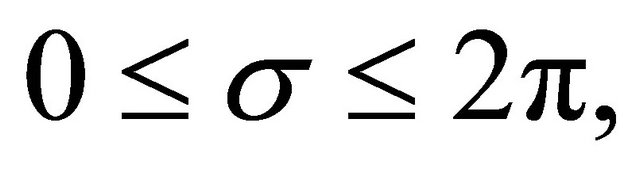
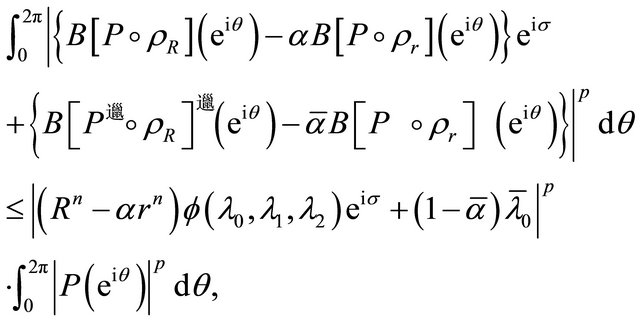 (2.10)
(2.10)
Proof. Let  and let
and let 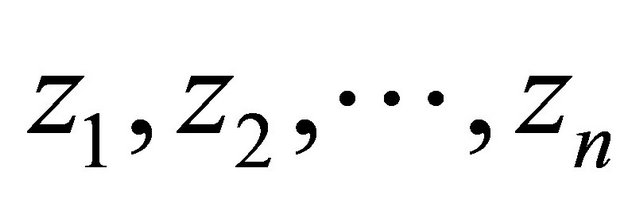 be the zeros of
be the zeros of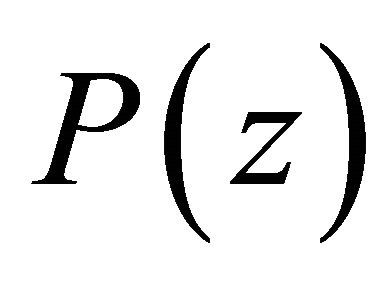 . If
. If 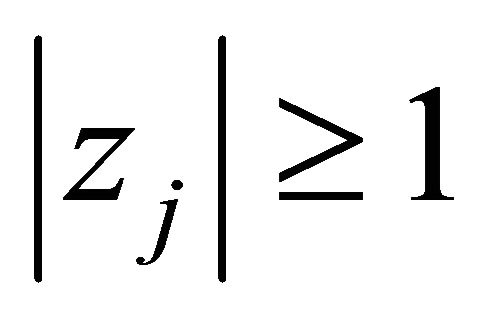 for all
for all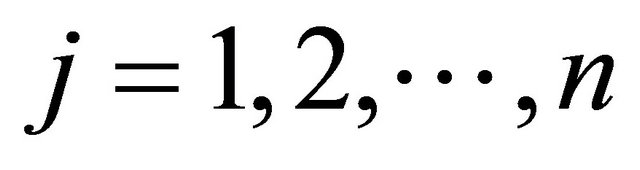 , then the result follows by Lemma 5. Henceforth, we assume that
, then the result follows by Lemma 5. Henceforth, we assume that 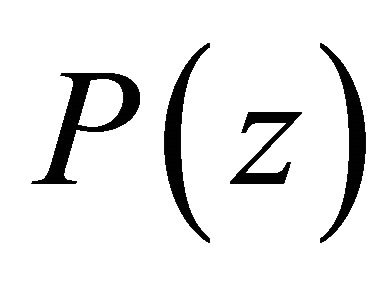 has at least one zero in
has at least one zero in  so that we can write
so that we can write

where the zeros  of
of 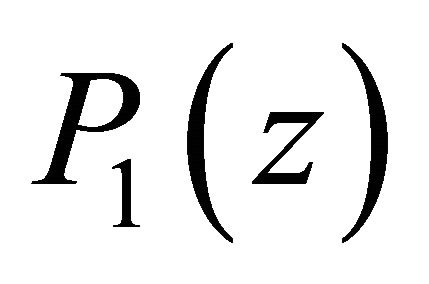 lie in
lie in 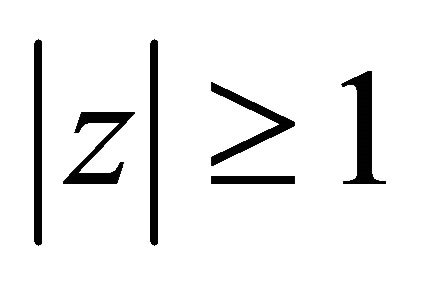 and the zeros
and the zeros 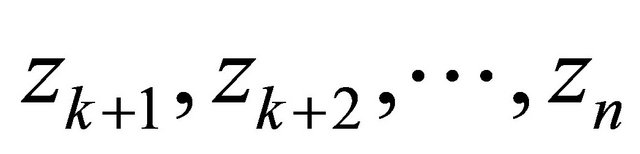 of
of 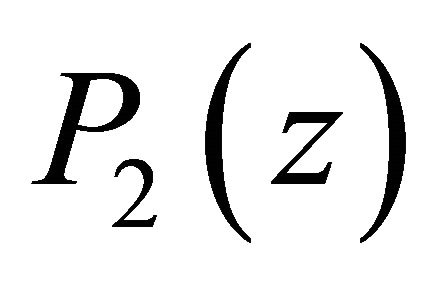 lie in
lie in 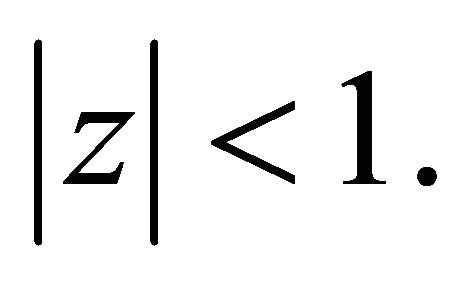 First we suppose that
First we suppose that 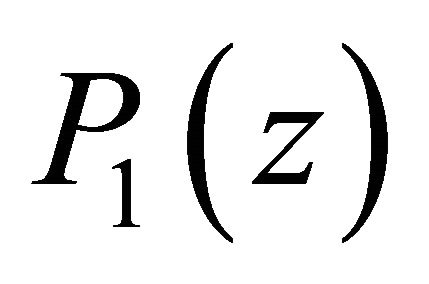 has no zero on
has no zero on  so that all the zeros of
so that all the zeros of  lie in
lie in 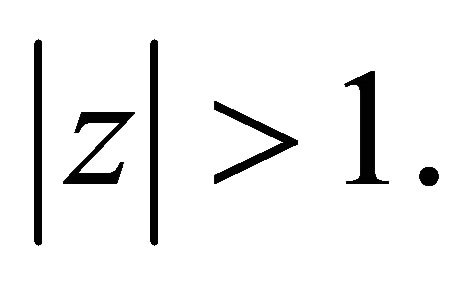 Since all the zeros of
Since all the zeros of 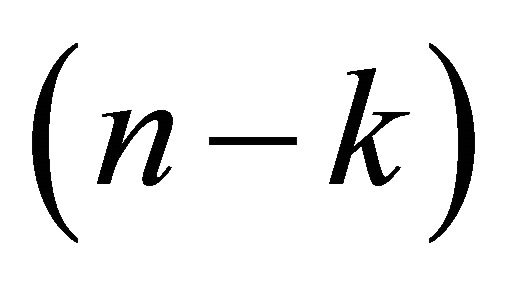 th degree polynomial
th degree polynomial  lie in
lie in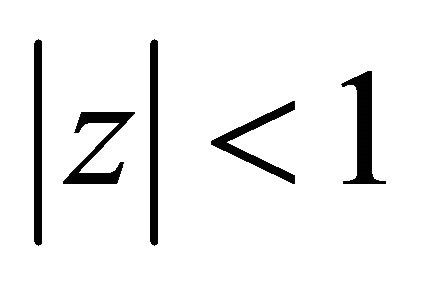 , all the zeroes of its conjugate polynomial
, all the zeroes of its conjugate polynomial
 lie in
lie in 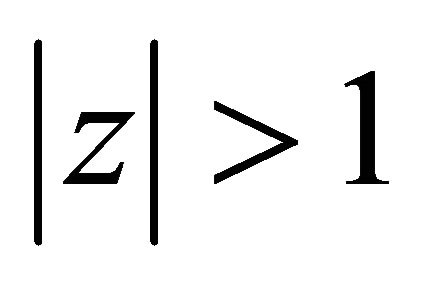 and
and
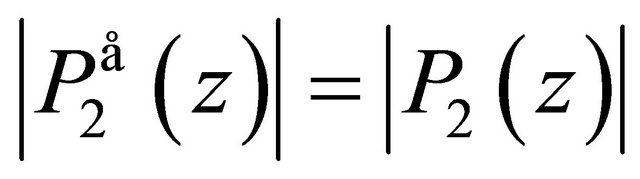 for
for 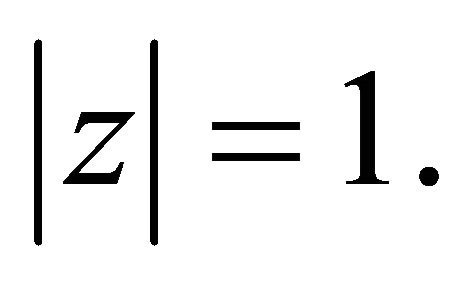 Now consider the polynomial
Now consider the polynomial
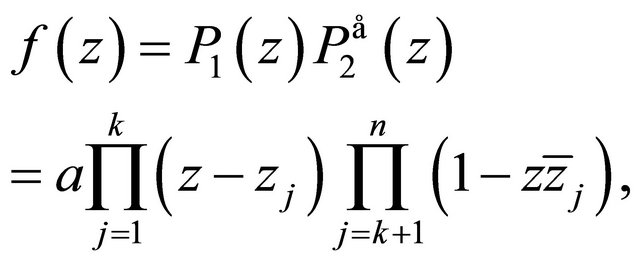
then all the zeroes of  lie in
lie in , and for
, and for 
 (2.11)
(2.11)
Therefore, it follows by Rouche’s Theorem that the polynomial  has all its zeros in
has all its zeros in 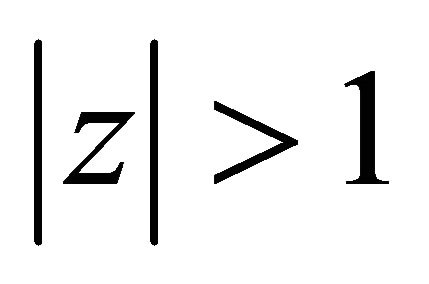 for every
for every 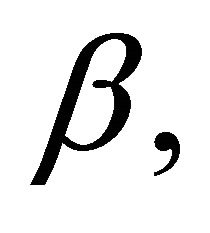 with
with 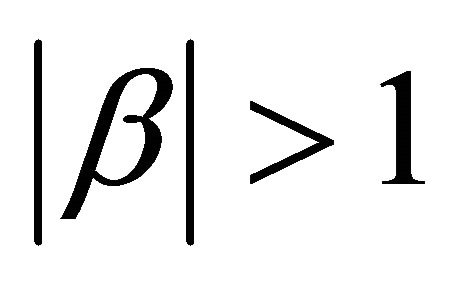 so that all the zeros of
so that all the zeros of 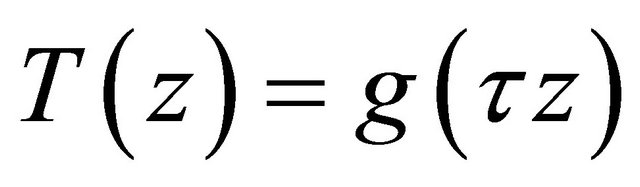 lie in
lie in 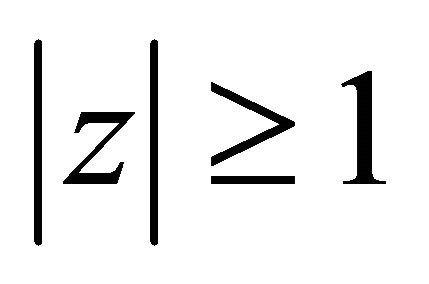 for some
for some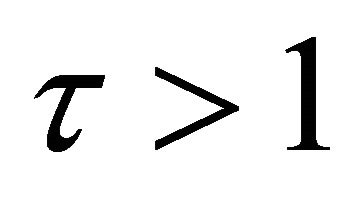 . Applying (2.9) and (2.8) to the polynomial
. Applying (2.9) and (2.8) to the polynomial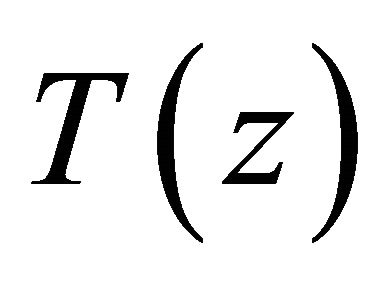 , we get for
, we get for  and
and 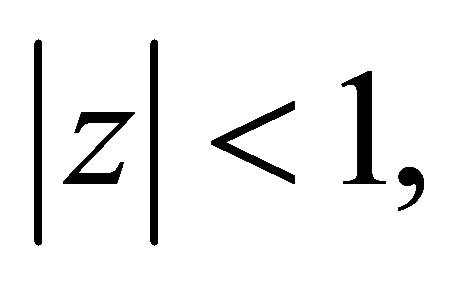
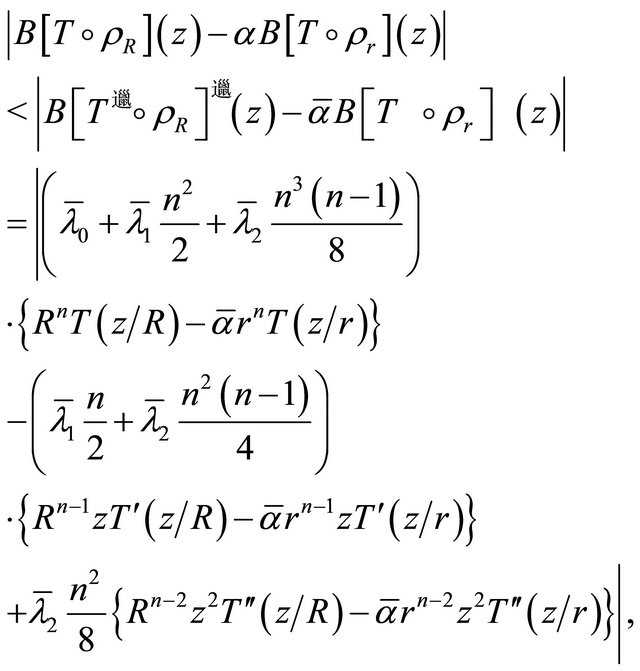
that is,
 (2.12)
(2.12)
for 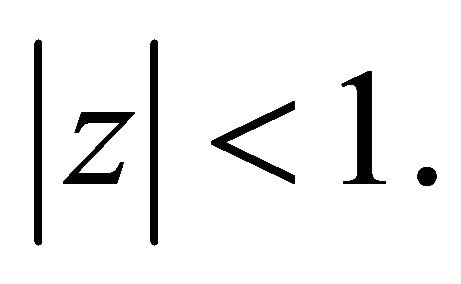 If
If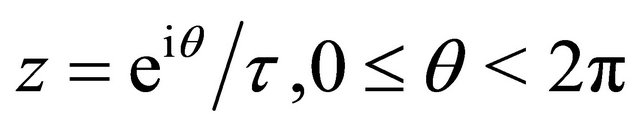 , then
, then 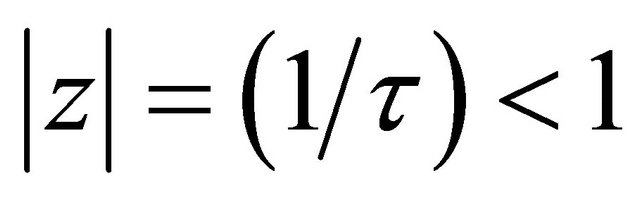 as
as 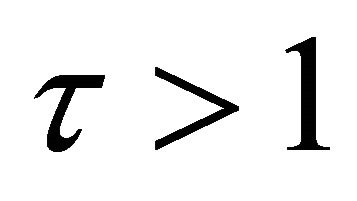 and we get
and we get
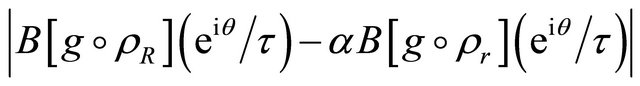
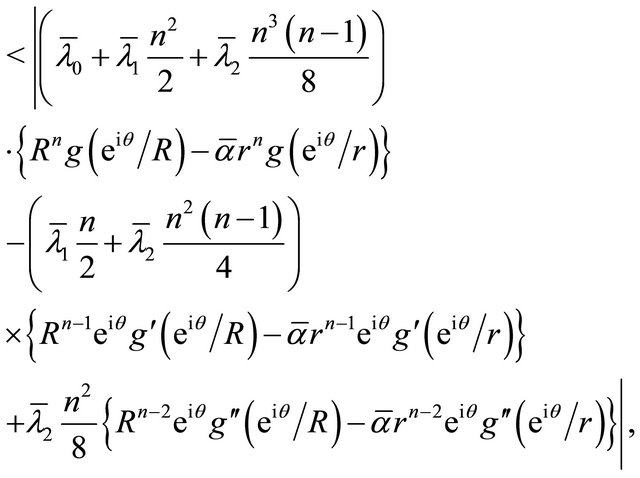
Equivalently, for 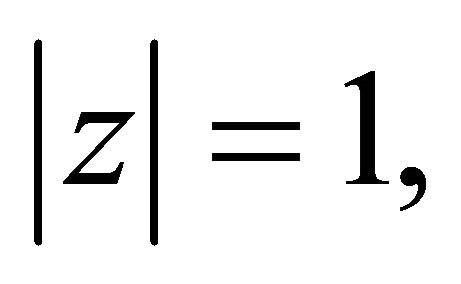
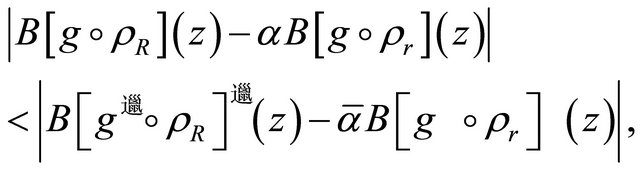
where 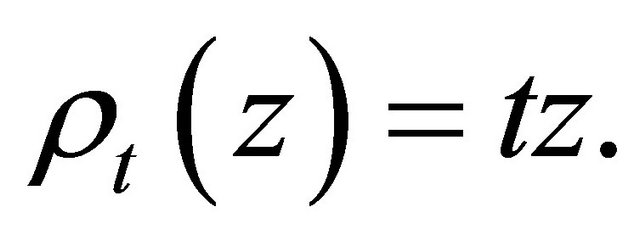
Since 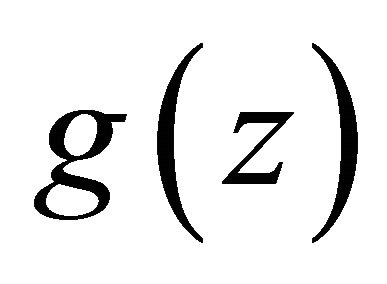 has all its zeros in
has all its zeros in 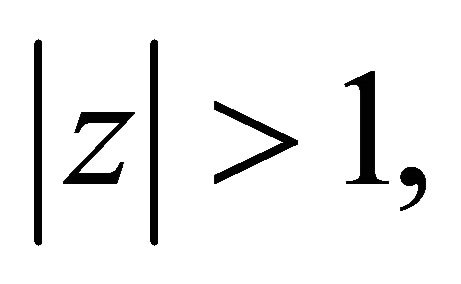 it follows that
it follows that 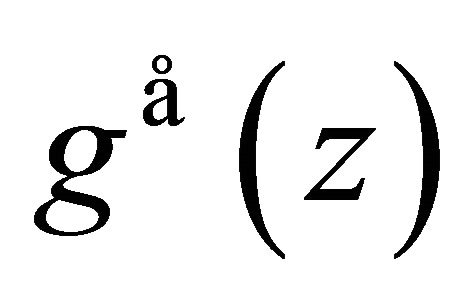 has its zeros in
has its zeros in  and hence (proceeding similarly as in proof of Lemma 3) the polynomial
and hence (proceeding similarly as in proof of Lemma 3) the polynomial 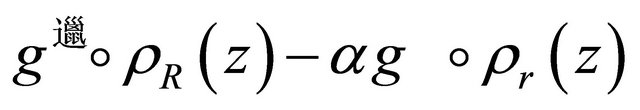 also has all its zeros in
also has all its zeros in 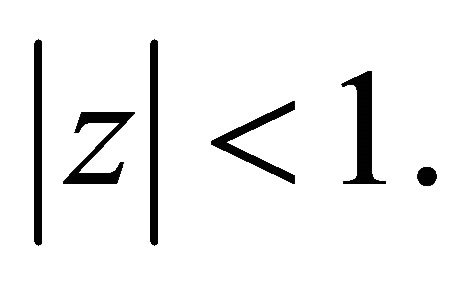 By Lemma 1,
By Lemma 1,
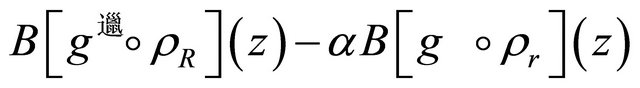 has all zeros in
has all zeros in
 and thus
and thus 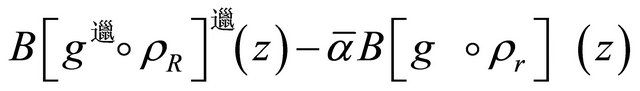 does not vanish in
does not vanish in 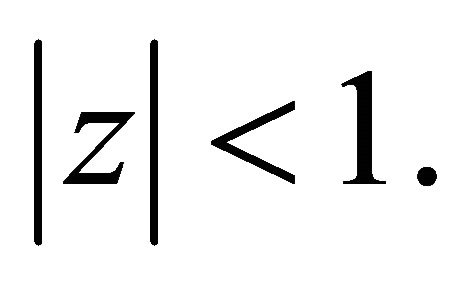
An application of Rouche’s theorem shows that the polynomial
 (2.13)
(2.13)
has all zeros in  Writing in
Writing in
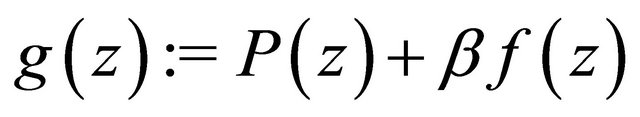 and noting that B is a linear operator, it follows that the polynomial
and noting that B is a linear operator, it follows that the polynomial
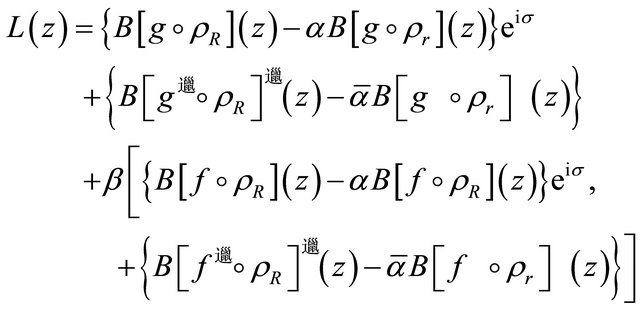 (2.14)
(2.14)
has all its zeros in 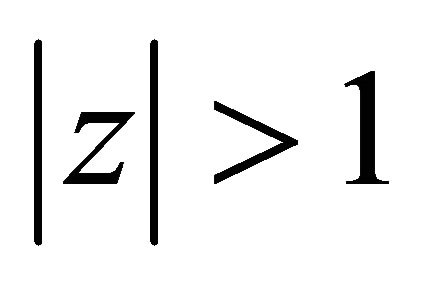 for every
for every 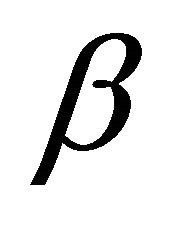 with
with 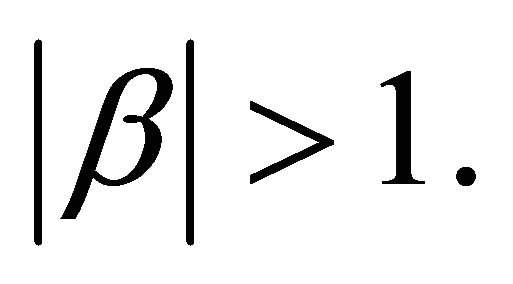
We claim
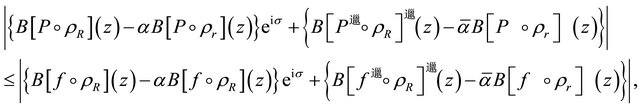 (2.15)
(2.15)
for 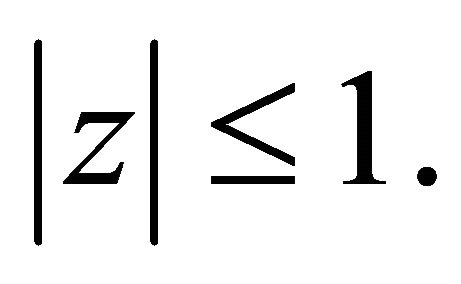 If Inequality (2.15) is not true, then there exists a point
If Inequality (2.15) is not true, then there exists a point 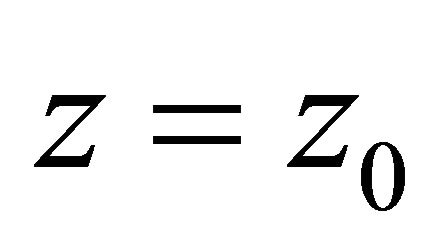 with
with  such that
such that
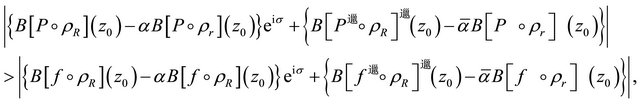
Since  has all its zeros in
has all its zeros in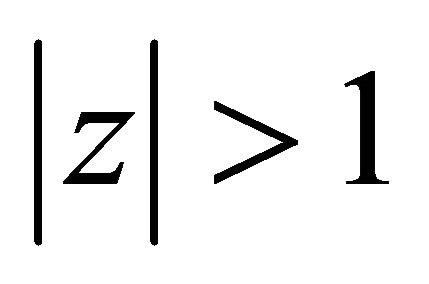 , proceeding similarly as in the proof of (2.13), it follows that
, proceeding similarly as in the proof of (2.13), it follows that
 for
for 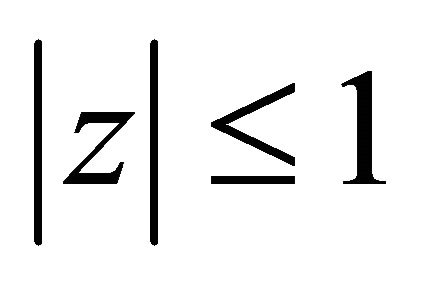 We take
We take

so that 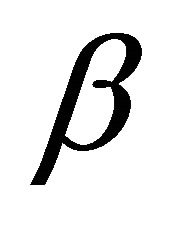 is a well-defined real or complex number with
is a well-defined real or complex number with 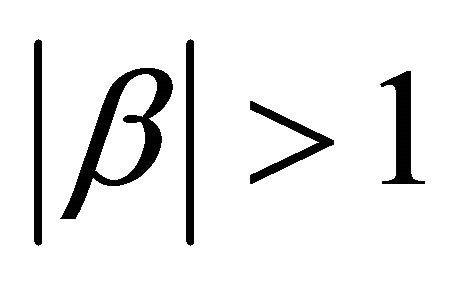 and with this choice of
and with this choice of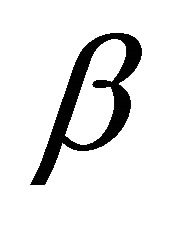 , from (2.14), we get
, from (2.14), we get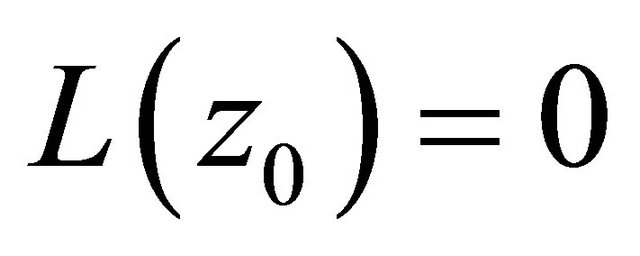 . This clearly is a contradiction to the fact that
. This clearly is a contradiction to the fact that 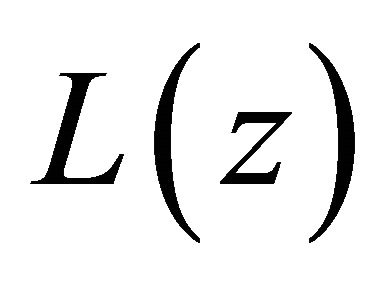 has all its zeros in
has all its zeros in 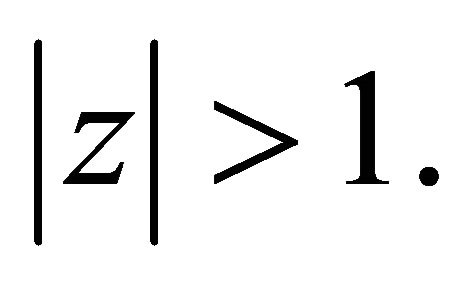 Thus (2.15) holds, which in particular gives for each
Thus (2.15) holds, which in particular gives for each 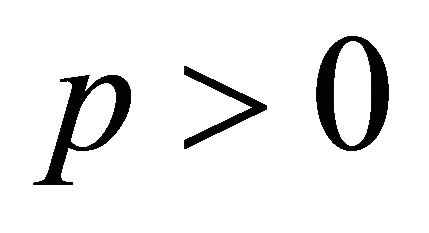 and
and ![]() real,
real,
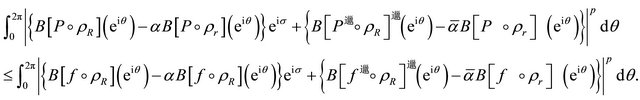
Lemma 4 and (2.7) applied to 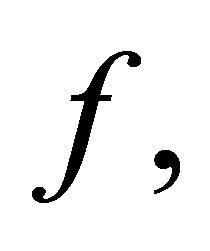 gives for each
gives for each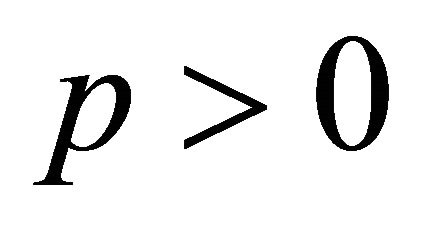 ,
,
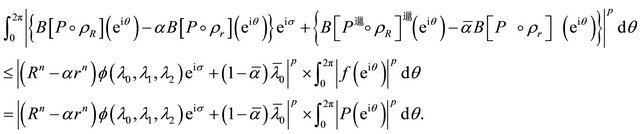 (2.16)
(2.16)
Now if  has a zero on
has a zero on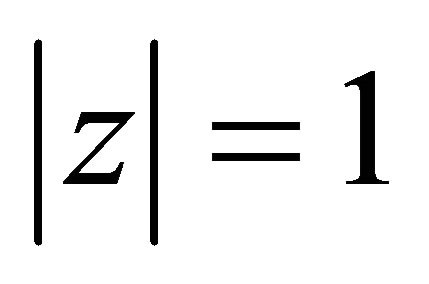 , then applying (2.16) to the polynomial
, then applying (2.16) to the polynomial 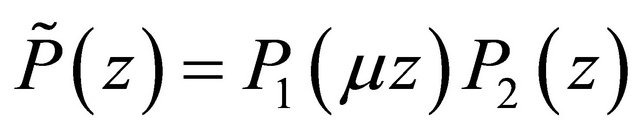 where
where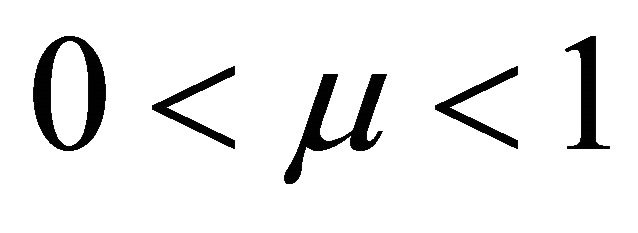 , we get for each
, we get for each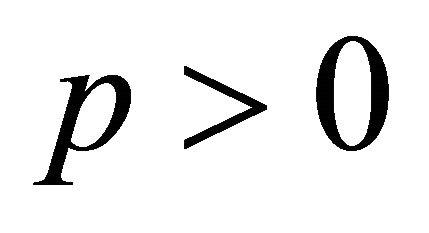 ,
, 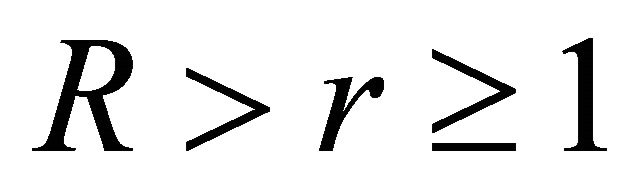 and
and ![]() real,
real,
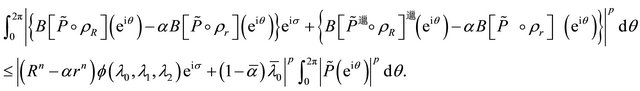 (2.17)
(2.17)
Letting 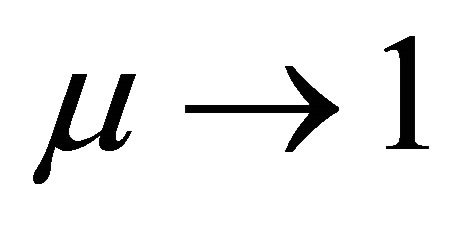 in (2.17) and using continuity, the desired result follows immediately and this proves Lemma 6.
in (2.17) and using continuity, the desired result follows immediately and this proves Lemma 6.
Lemma 7. If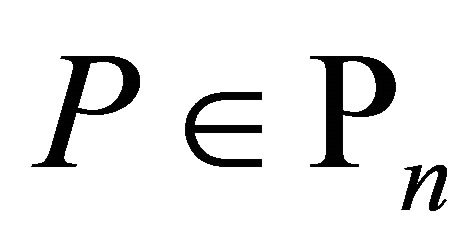 , then for every
, then for every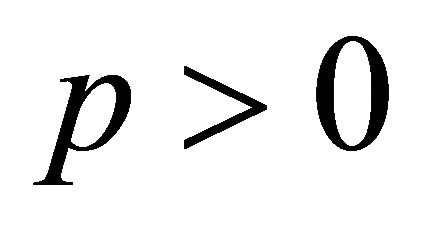 ,
, 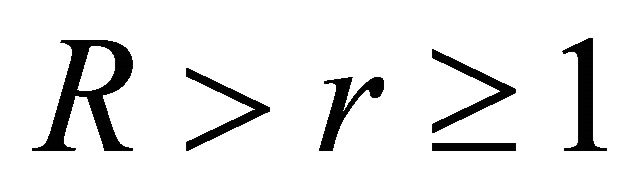 and
and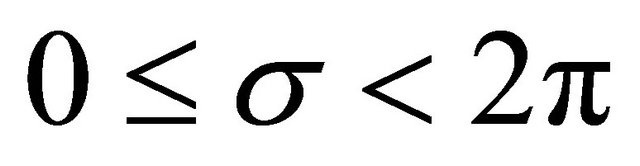 ,
,
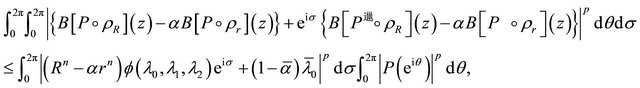 (2.18)
(2.18)
where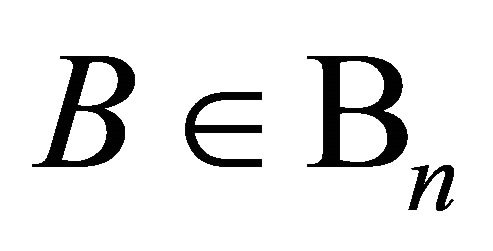 ,
,  and
and  is defined by (1.13). The result is best possible and
is defined by (1.13). The result is best possible and 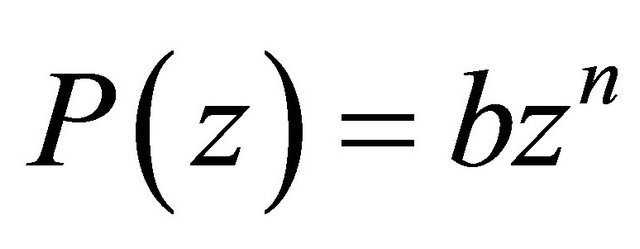 is an extremal polynomial for any
is an extremal polynomial for any 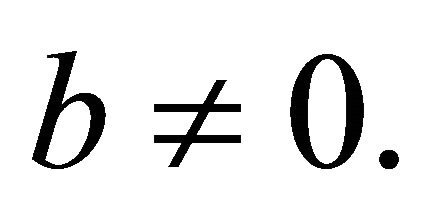
Proof. By Lemma 6, for each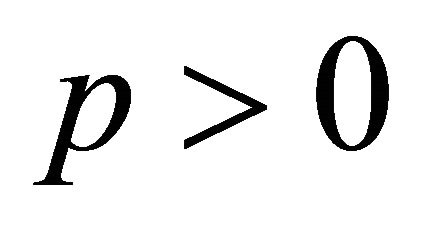 ,
, 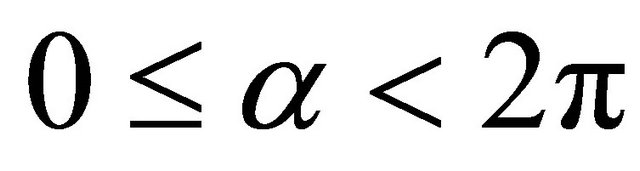 and
and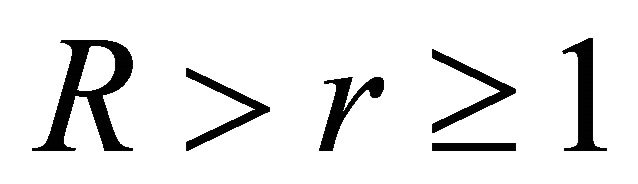 , the Inequality (2.6) holds. Since
, the Inequality (2.6) holds. Since
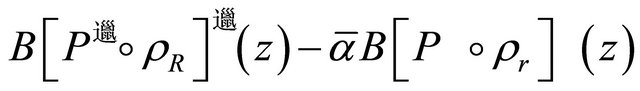 is the conjugate polynomial of
is the conjugate polynomial of ,
,
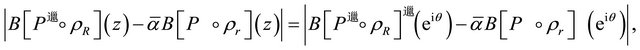
and therefore for each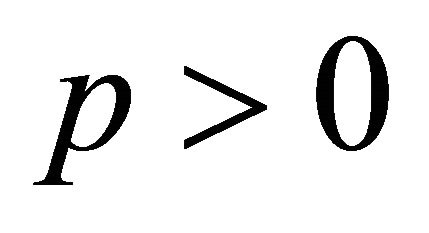 ,
, 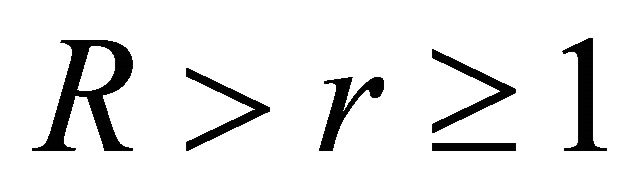 and
and 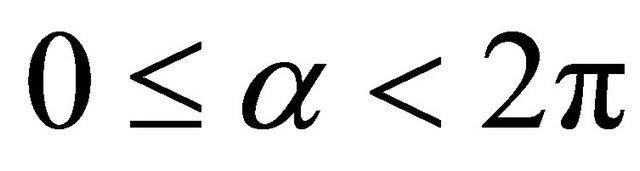 , we have
, we have
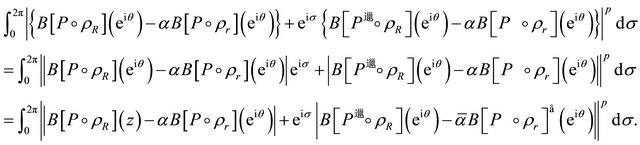 (2.19)
(2.19)
Integrating (2.19) both sides with respect to  from 0 to
from 0 to  and using (2.6), we get
and using (2.6), we get
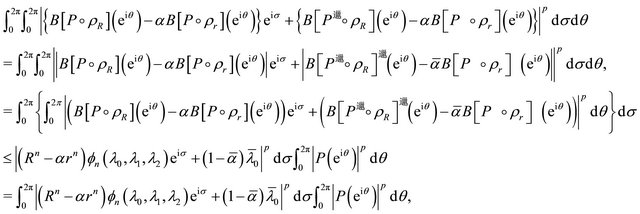
which establishes Inequality (2.18).
3. Proof of Theorems
Proof of Theorem. By hypothesis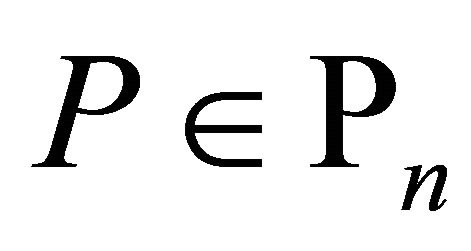 , we can write
, we can write
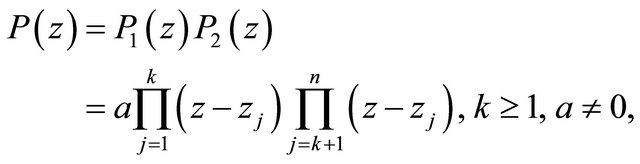
where the zeros 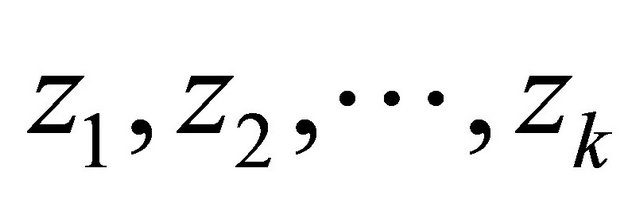 of
of 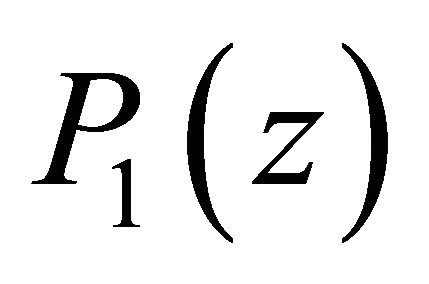 lie in
lie in 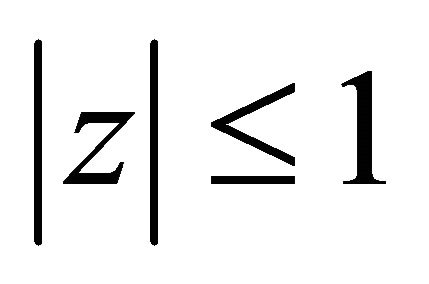 and the zeros
and the zeros 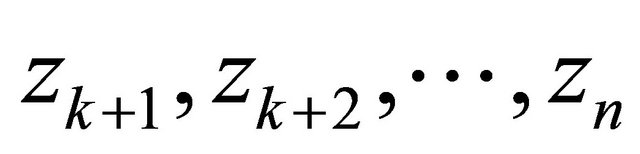 of
of 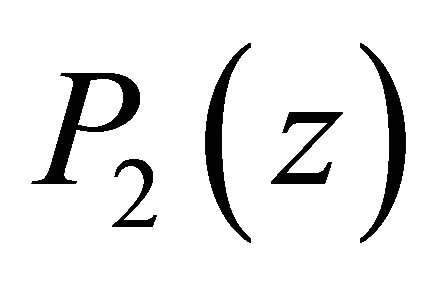 lie in
lie in 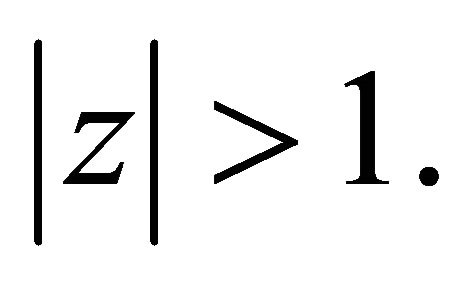 First, we suppose that all the zeros of
First, we suppose that all the zeros of  lie in
lie in 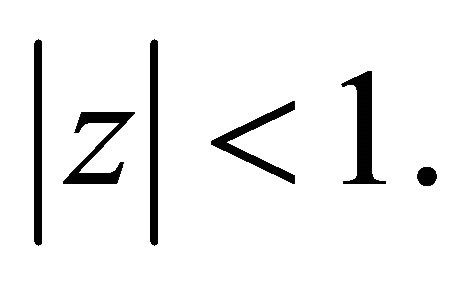 Since all the zeros of
Since all the zeros of  lie in
lie in , the polynomial
, the polynomial 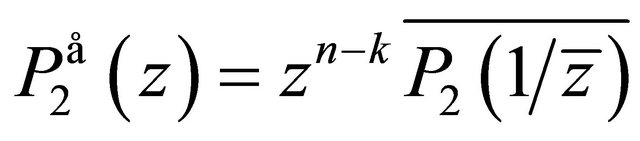 has all its zeroes in
has all its zeroes in
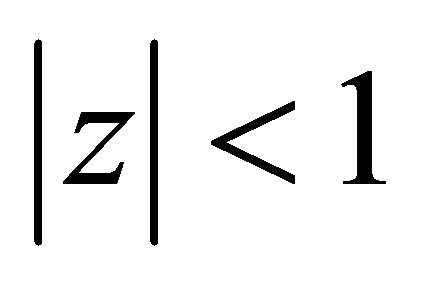 and
and  for
for  Now consider the polynomial
Now consider the polynomial
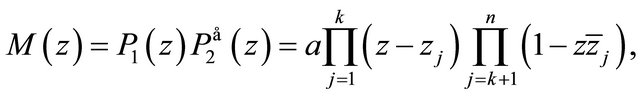
then all the zeros of 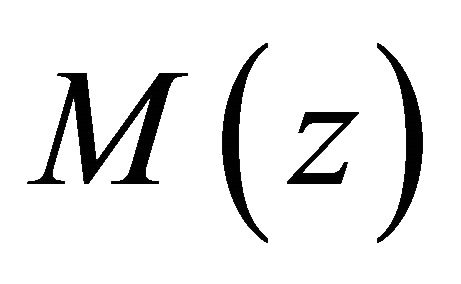 lie in
lie in  and for
and for 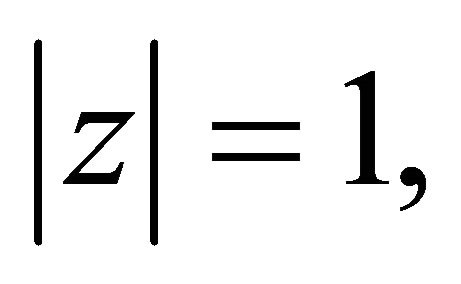
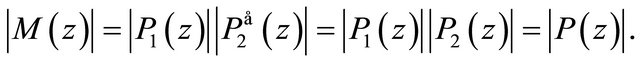 (3.1)
(3.1)
Observe that 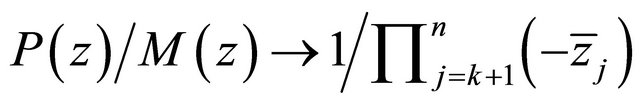 when
when
![]() , so it is regular even at
, so it is regular even at  and thus from (3.1) and by the maximum modulus principle, it follows that
and thus from (3.1) and by the maximum modulus principle, it follows that
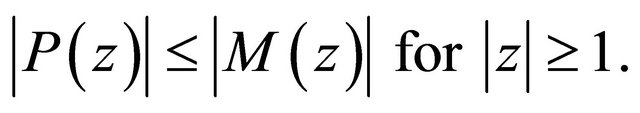
Since 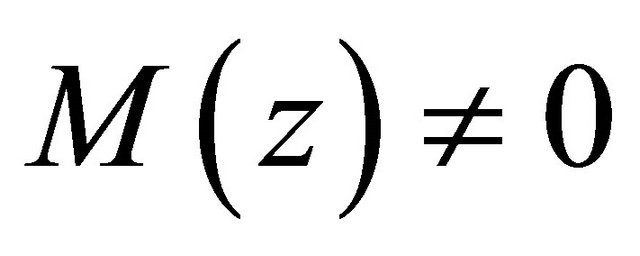 for
for 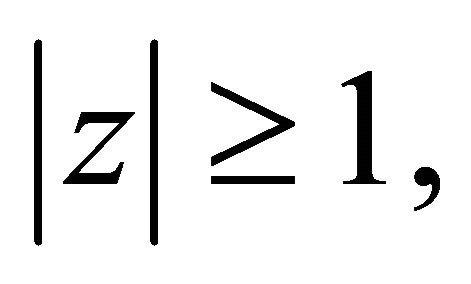 a direct application of Rouche’s theorem shows that the polynomial
a direct application of Rouche’s theorem shows that the polynomial 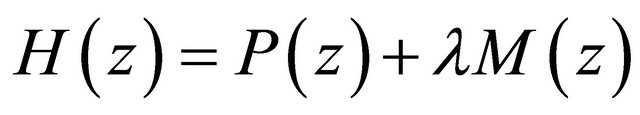 has all its zeros in
has all its zeros in 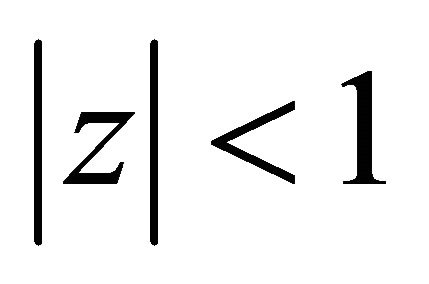 for every
for every ![]() with
with 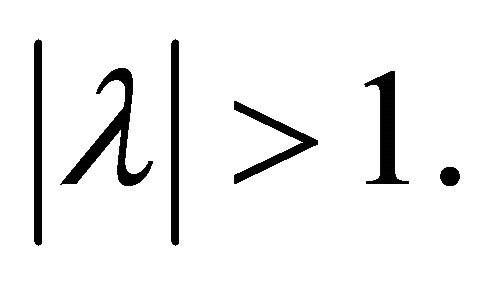 Applying Lemma 2 to the polynomial
Applying Lemma 2 to the polynomial 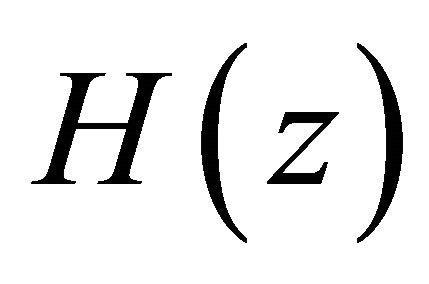 and noting that the zeros of
and noting that the zeros of 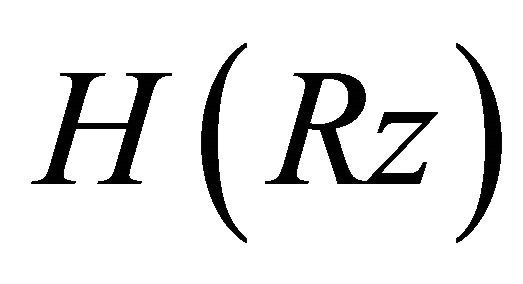 lie in
lie in 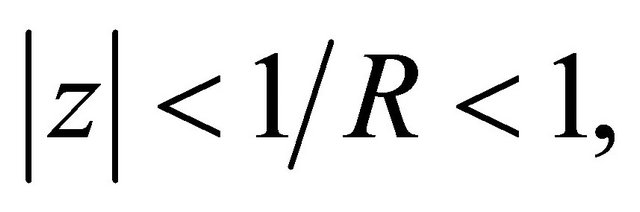 we deduce (as in Lemma 3) that for every real or complex
we deduce (as in Lemma 3) that for every real or complex ![]() with
with 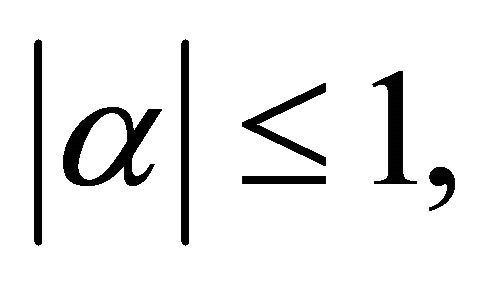 all the zeros of polynomial
all the zeros of polynomial
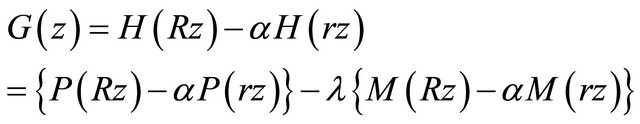
lie in  Applying Lemma 1 to
Applying Lemma 1 to 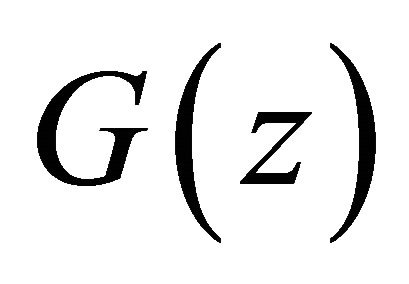 and noting that
and noting that 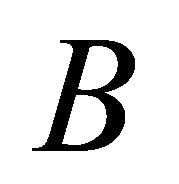 is a linear operator, it follows that all the zeroes of
is a linear operator, it follows that all the zeroes of
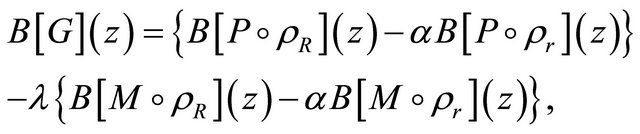
lie in 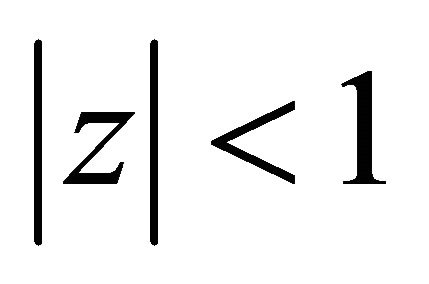 for every
for every ![]() with
with 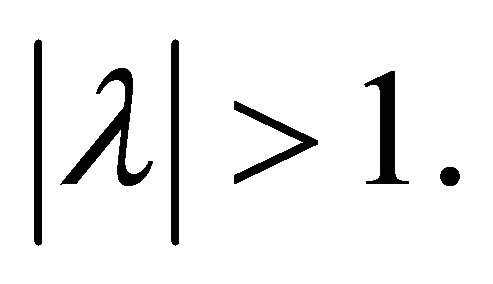 This implies for
This implies for 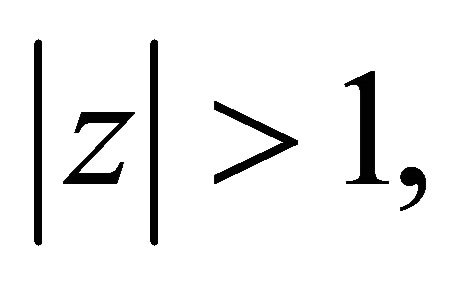
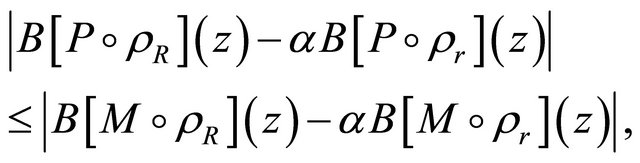
which, in particular, gives for each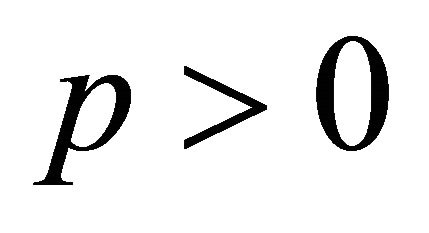 ,
, 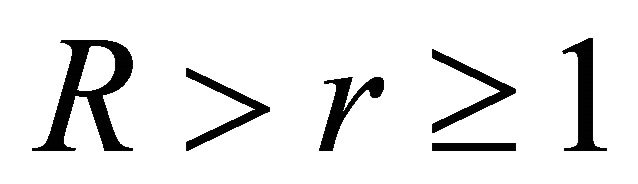 and
and ,
,
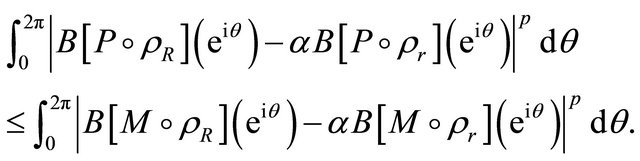 (3.2)
(3.2)
Again,(as in case of )
)  has all its zeros in
has all its zeros in  thus by Lemma 1,
thus by Lemma 1,
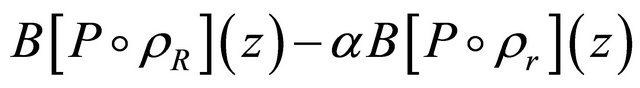 also has all its zeros in
also has all its zeros in
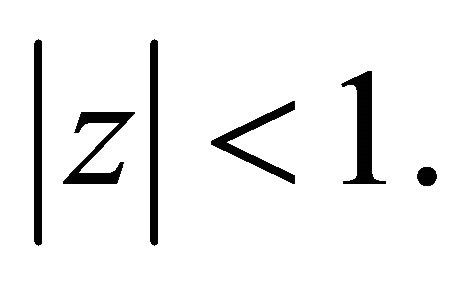 Therefore, if
Therefore, if  has all its zeros in
has all its zeros in 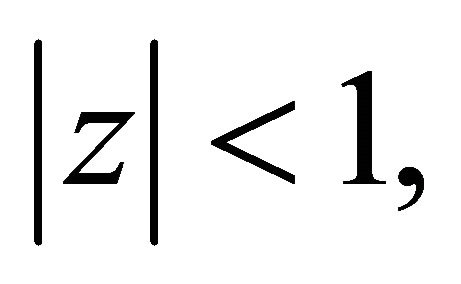 then the operator
then the operator  defined by
defined by
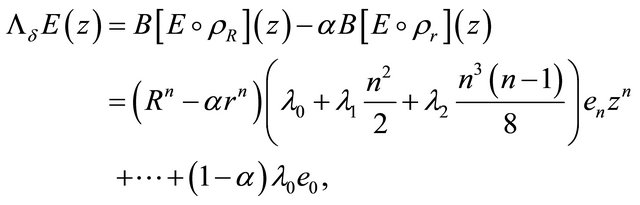
(3.3)
is admissible. Since 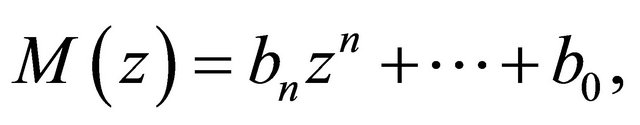 has all its zeros in
has all its zeros in 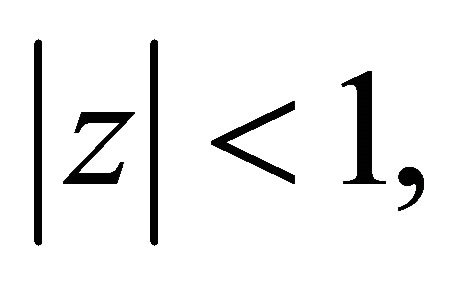 in view of (3.3) it follows by (2.5) of Lemma 4 that for each
in view of (3.3) it follows by (2.5) of Lemma 4 that for each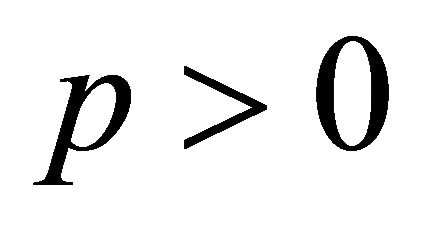 ,
,
 (3.4)
(3.4)
Combining Inequalities (3.3), (3.4) and noting that
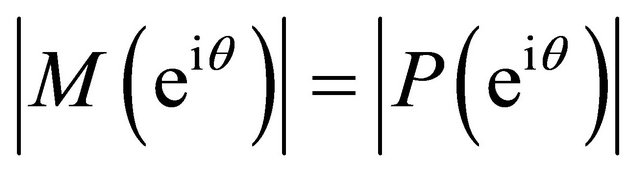 , we obtain for each
, we obtain for each 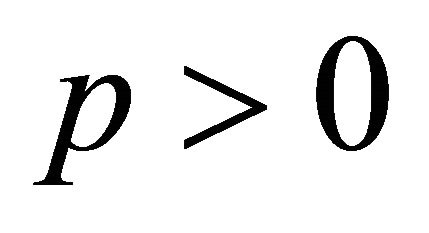 and
and
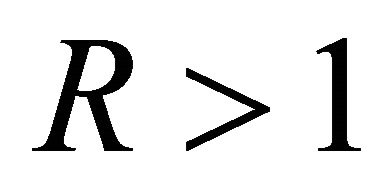 ,
,
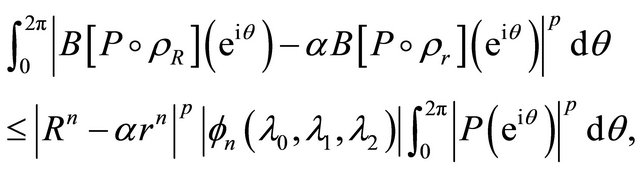 (3.5)
(3.5)
In case  has a zero on
has a zero on , then Inequality (3.5) follows by continuity. This proves Theorem 1 for
, then Inequality (3.5) follows by continuity. This proves Theorem 1 for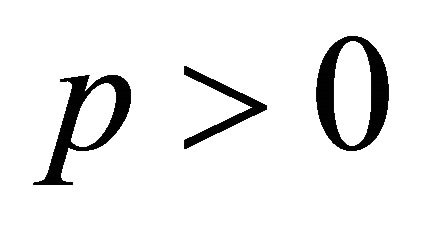 . To obtain this result for
. To obtain this result for , we simply make
, we simply make .
.
Proof of Theorem 2. By hypothesis 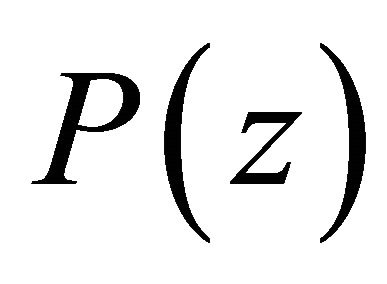 does not vanish in
does not vanish in 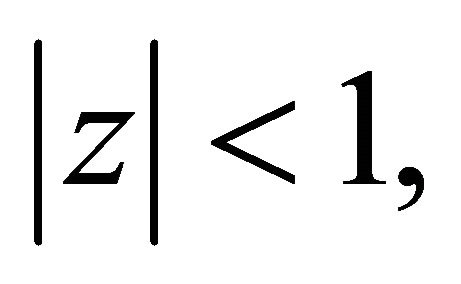
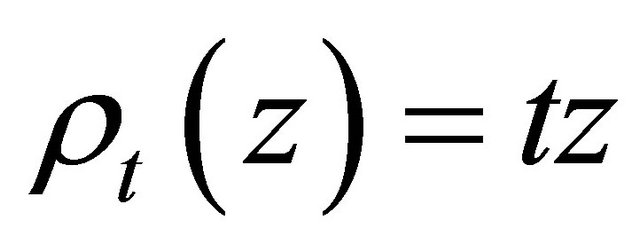 and
and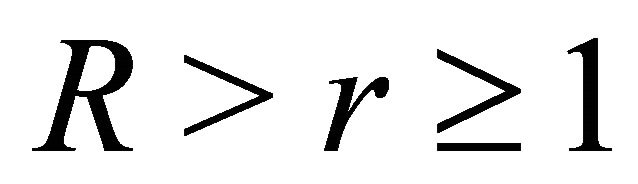 , therefore, for
, therefore, for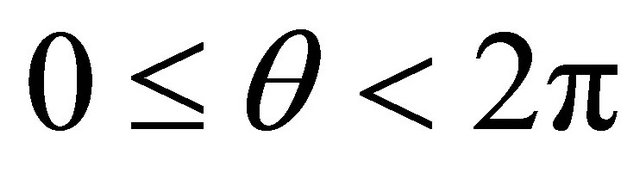 , (2.1) holds. Also, for each
, (2.1) holds. Also, for each 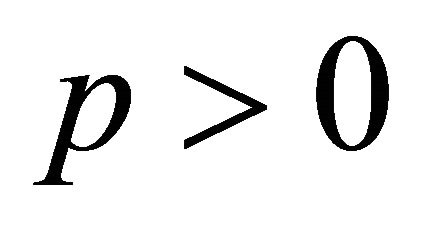 and
and ![]() real, (2.18) holds.
real, (2.18) holds.
Now it can be easily verified that for every real number ![]() and
and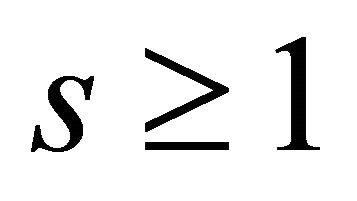 ,
,
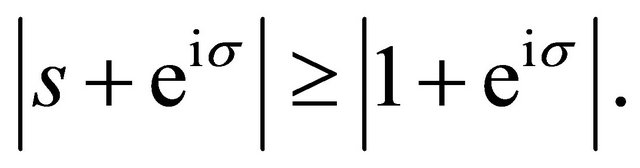
This implies for each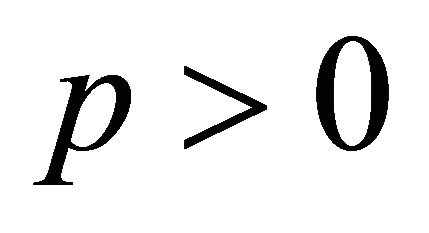 ,
,
 (3.6)
(3.6)
If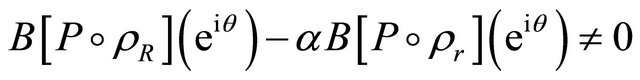 , we take
, we take
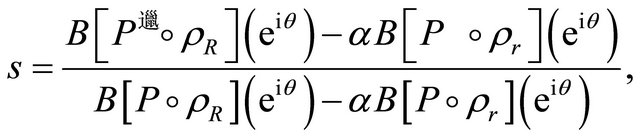
then by (2.1), and we get with the help of (3.6),
and we get with the help of (3.6),
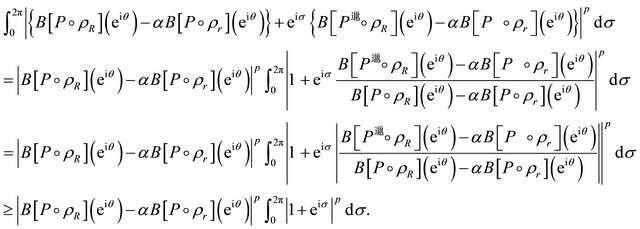
For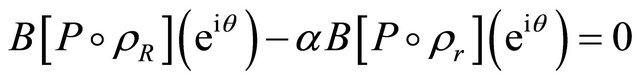 , this inequality is trivially true. Using this in (2.18), we conclude that for each
, this inequality is trivially true. Using this in (2.18), we conclude that for each ,
,
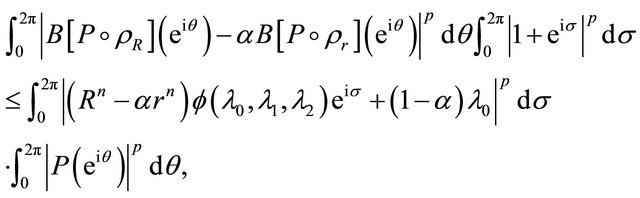
from which Theorem 2 follows for . To establish this result for
. To establish this result for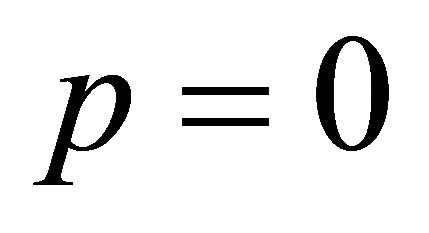 , we simply let
, we simply let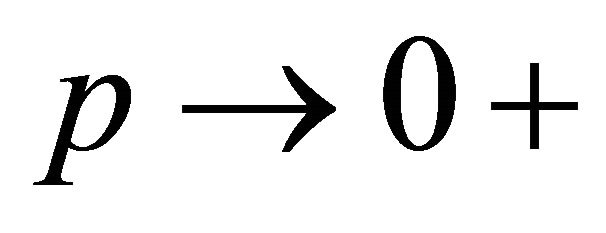 .
.
Proof of Theorem 3. Since 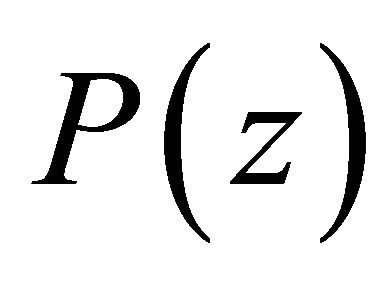 is a self-inversive polynomial, then we have for some
is a self-inversive polynomial, then we have for some![]() , with
, with 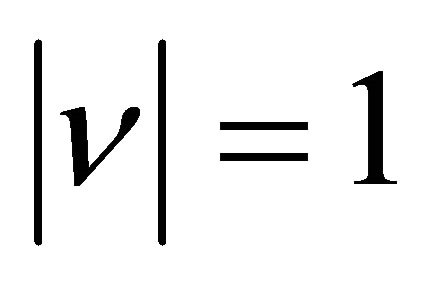
 for all
for all , where
, where 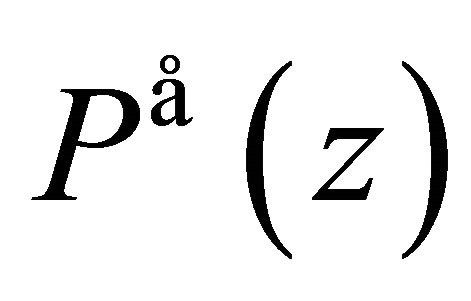 is the conjugate polynomial
is the conjugate polynomial . This gives, for
. This gives, for 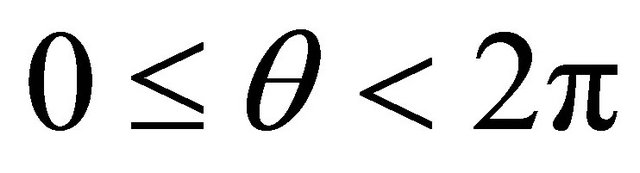
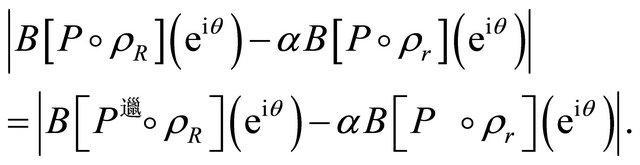
Using this in place of (2.1) and proceeding similarly as in the proof of Theorem 2, we get the desired result for each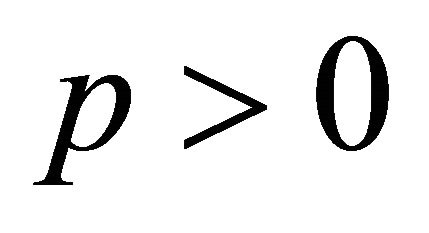 . The extension to
. The extension to 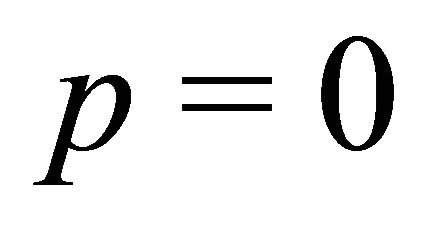 obtains by letting
obtains by letting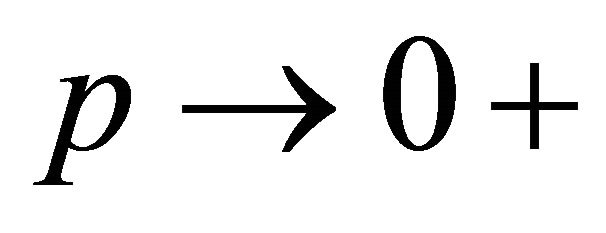 .
.
REFERENCES
- W. M. Shah and A. Liman, “Integral Estimates for the Family of B-Operators,” Operator and Matrices, Vol. 5, No. 1, 2011, pp. 79-87. doi:10.7153/oam-05-04
- Q. I. Rahman, “Functions of Exponential Type,” Transactions of the American Society, Vol. 135, 1969, pp. 295-309. doi:10.1090/S0002-9947-1969-0232938-X
- G. Pólya an G. Szegö, “Aufgaben und Lehrsätze aus der Analysis,” Springer-Verlag, Berlin, 1925.
- Q. I. Rahman and G. Schmessier, “Analytic Theory of Polynomials,” Claredon Press, Oxford, 2002.
- A. C. Schaffer, “Inequalities of A. Markoff and S. Bernstein for Polynomials and Related Functions,” Bulletin of the American Mathematical Society, Vol. 47, No. 8, 1941, pp. 565-579. doi:10.1090/S0002-9904-1941-07510-5
- G. V. Milovanovic, D. S. Mitrinovic and Th. M. Rassias, “Topics in Polynomials: Extremal Properties, Inequalities,” Zeros, World Scientific Publishing Co., Singapore City, 1994.
- A. Zugmund, “A Remark on Conjugate Series,” Proceedings London Mathematical Society, Vol. 34, No. 2, 1932, pp. 292-400.
- G. H. Hardy, “The Mean Value of the Modulus of an Analytic Function,” Proceedings London Mathematical Society, Vol. 14, 1915, pp. 269-277. doi:10.1112/plms/s2_14.1.269
- Q. I. Rahman and G. Schmessier, “Les Inequalitués de Markoff et de Bernstein,” Presses University Montréal, Montréal, Quebec, 1983.
- M. Riesz, “Formula d’Interpolation pour la Dérivée d’un Polynome Trigonométrique,” Comptes Rendus de l’Académie des Sciences, Vol. 158, 1914, pp. 1152-1254.
- V. V. Arestov, “On Integral Inequalities for Trigonometric Polynimials and Their Derivatives,” Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, Vol. 45, No. 1, 1981, pp. 3-22.
- P. D. Lax, “Proof of a Conjecture of P. Erdös on the Derivative of a Polynomial,” Bulletin of the American Mathematical Society, Vol. 50, No. 5, 1944, pp. 509-513. doi:10.1090/S0002-9904-1944-08177-9
- N. C. Ankeny and T. J. Rivilin, “On a Theorm of S. Bernstein,” Pacific Journal of Mathematics, Vol. 5, 1955, pp. 849-852. doi:10.2140/pjm.1955.5.849
- N. G. Brijn, “Inequalities Concerning Polynomials in the Complex Domain,” Nederlandse Akademie Van Wetenschappen, Vol. 50, 1947, pp. 1265-1272.
- Q. I. Rahman and G. Schmessier, “Lp Inequalities for Polynomials,” Journal of Approximation Theory, Vol. 53, No. 1, 1988, pp. 26-32. doi:10.1016/0021-9045(88)90073-1
- R. P. Boas Jr. and Q. I. Rahman, “Lp Inequalities for Polynomials and Entire Functions,” Archive for Rational Mechanics and Analysis, Vol. 11, No. 1, 1962, pp. 34-39. doi:10.1007/BF00253927
- K. K. Dewan and N. K. Govil, “An Inequality for Self-Inversive Polynomials,” Journal of Mathematical Analysis and Applications, Vol. 45, 1983, p. 490. doi:10.1016/0022-247X(83)90122-1
- A. Aziz, “A New Proof of a Theorem of De Bruijn,” Proceedings of the American Mathematical Society, Vol. 106, No. 2, 1989, pp. 345-350. doi:10.1090/S0002-9939-1989-0933511-6
- A. Aziz and N. A. Rather, “Some Compact Generalizations of Zygmund-Type Inequalities for Polynomials,” Nonlinear Studies, Vol. 6, No. 2, 1999, pp. 241-255.
- M. Marden, “Geometry of Polynomials,” Mathematical Surveys, No. 3, American Mathematical Society, Providence, 1966.

