Applied Mathematics
Vol.3 No.10A(2012), Article ID:24134,7 pages DOI:10.4236/am.2012.330202
Artificial Searching Swarm Algorithm and Its Performance Analysis
Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability, Hebei University of Technology, Tianjin, China
Email: tgchen@hebut.edu.cn
Received July 9, 2012; revised August 9, 2012; accepted August 16, 2012
Keywords: Artificial Searching Swarm Algorithm; Bionic Intelligent Optimization Algorithm; Optimization; Evolutionary Computation; Swarm Intelligence
ABSTRACT
Artificial Searching Swarm Algorithm (ASSA) is a new optimization algorithm. ASSA simulates the soldiers to search an enemy’s important goal, and transforms the process of solving optimization problem into the process of searching optimal goal by searching swarm with set rules. This work selects complicated and highn dimension functions to deeply analyse the performance for unconstrained and constrained optimization problems and the results produced by ASSA, Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Artificial Fish-Swarm Algorithm (AFSA) have been compared. The main factors which influence the performance of ASSA are also discussed. The results demonstrate the effectiveness of the proposed ASSA optimization algorithm.
1. Introduction
Optimal design is always the goal in the engineering design fields. The traditional optimization algorithms often depend on the quality of the objective function, but many objective functions are usually highly non-linear, steep, multi-peak, non-differential or even discontinuous, and have many continual or discrete parameters. Almost all the problems need vast amount of computation. The traditional optimization techniques are incapable to solve these problems.
Most animals and insects show the amazing abilities of completing complex behaviors. Since 1940s, the optimization design problems in the engineering fields have been solved by using the inspiration of the biological systems, and meantime a new type of optimization method —Bionic Intelligent Optimization Algorithm (BIOA) is found. At present, the popular bionic intelligent optimization algorithms are Genetic Algorithm (GA) [1], Ant Colony Algorithm (ACA) [2], Particle Swarm Optimization (PSO) [3], Artificial Fish-Swarm Algorithm (AFSA) [4], and Shuffled Frog Leaping Algorithm (SFLA) [5]. These bionic algorithms have become a research focus in the fields of intelligent optimization.
Simulating a group soldiers to complete the task for searching the enemy’s important goals, a new bionic intelligent optimization algorithm—Artificial Searching Swarm Algorithm (ASSA) is presented and simply discussed [6]. In ASSA, the process of solving the optimization problem is transformed into the process of finding the optimal solution for searching swarm with set rules, then through the search and cooperation of searching individuals the optimal solution is expected to find. This work selects complicated and highn dimension functions to deeply analyse the performance for optimizing multivariable functions and the results produced by ASSA, GA, PSO, AFSA have been compared, and the main factors which influence the performance of ASSA are also discussed. Simulation tests showed that ASSA is an efficient optimization algorithm.
2. Abstract Model of BIOA
Although the characters are different, BIOA manifests the great similarity in the structure, operation model, research method and the research content. It provides the possibility for the establishment of abstract model.
The abstract model of BIOA can be described as follows: the swarm is formed by the individuals, relies on the specific evolution rules to generate the reborn swarm (such as GA) or change the individual position (such as PSO, AFSA), and goes with the iteration of the algorithm, the current solution evolves unceasingly along with the change of the swarm and then approaches the optimal solution gradually [7,8].
The process of the algorithms is shown as follows:
1) Set the parameters, initialize the swarm randomly and calculate the fitness values;
2) According to the set rules, renew swarm or its position, generate a group of solutions, and calculate the fitness of individuals;
3) Through comparison, obtain the optimal fitness value and take note;
4) Judge whether or not the terminal condition is satisfied. If satisfy, end the iteration; otherwise, return to 2.
In this abstract model, the rules of renewing swarm decide the algorithm performance. These set rules restrict the individual behaviors, and form the unique characteristics of the algorithm to be different from the other algorithms.
In BIOA the bulletin board is generally used to record the optimal individual’s historical states. Through the iteration of the algorithm, each individual compares its own condition with bulletin board’s condition, and replaces the information when its value is better. Thus the bulletin board can record the historical best solution all along. After algorithm iteration finished, the optimal solution and the related information can be obtained from the bulletin board.
3. Artificial Searching Swarm Algorithm
3.1. Basic Idea of ASSA
According to the abstract model of BIOA, ASSA uses the swarm composed of searching individuals as the executive to implement the searching task, and transforms the process of solving optimal design problem into the process of implementing relevant task and searching optimal goal of the searching swarm with set rules. Through the uninterrupted search of searching swarm, the better solution evolves unceasingly and approaches the optimal solution gradually, so the corresponding optimization problem is solved.
According to the above ideas, how to set the rules becomes the key problem. The rules of the algorithm are the limitation of the searching individual’s behavior, which decide directly the searching swarm’s movement mechanism, and affect the efficiency and the success of the algorithm.
The searching individual behaviors can be described as follows:
1) Synergetic move rule: basic communication relation is kept between searching individuals. If an individual receives a call sent by the other individuals, it moves forward to the called individual’s position by a step with a certain probability;
2) Reconnaissance move rule: If the individual does not receive the call, it implements reconnaissance according to it’s and swarm’s historical experience. If finds a better goal, then moves forward to the position by a step;
3) Stochastic move rule: If the searching individual does not receive a call, and does not find a better goal, it moves a step randomly.
If finds a better goal during above moves, sends a call to searching swarm.
Three rules of the ASSA have their own characteristics. Rule 1 can compel the searching swarm moving forward to the better goal, and accelerate the convergence speed of the algorithm; Rule 2 plays a main role in finding the better goals, pulls the algorithm away from the local solution, and has the global adjusting function; Rule 3 plays a supporting role in moving swarm. The above analyses have been confirmed by simulation tests.
The running flow of ASSA is shown as follows:
1) Set the parameters, initialize the swarm randomly and calculate the fitness value;
2) Iteration counter add 1, deal with the individuals in turn as follows:
a) If receive a call, then move forward to the called individual by a step with a certain probability;
b) Otherwise, according to its own and swarm’s historical experience, implement the reconnaissance. If find a better goal, move forward to the better goal by a step;
c) Or move by a step randomly.
If find the better goal during above moves, send a call to searching swarm.
3) Calculate the fitness value. Compare with the best fitness of swarm and each individual respectively, if better, log on the bulletin board;
4) Determine whether or not to satisfy the conditions of termination, if satisfy, then end the iteration; otherwise, return to 2.
3.2. Pseudo-Code Description of the ASSA
For explaining the behavior rule clearly, by using objectoriented technology, a searching individual can be described as a C++ class as follows:
class Artificial_Searching_Individuals
{
float X[n]; //individual’s position.
float AS_step; //the distance moved for a step float Pc; //synergetic parameter, the value of probability to implement the synergetic move rule float AS_fitness(); //the object function void AS_synergetic(); //the behavior of synergetic void AS_reconnaissance(); //the behavior of reconnaissance void AS_move(); //the behavior of move Artificial_Searching_Individuals();
virtual~Artificial_Searching_Individuals();
};
Suppose r1, r2, r3 are three random real numbers, 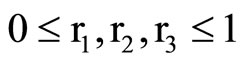 , the individual’s position is Xi in i-th iteration, the historical best solution of the individual is Xs, the historical best solution of the swarm is Xg, the location of the called individual which find the better goal is Xcall, the distance function is
, the individual’s position is Xi in i-th iteration, the historical best solution of the individual is Xs, the historical best solution of the swarm is Xg, the location of the called individual which find the better goal is Xcall, the distance function is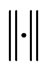 , and the absolute value function is
, and the absolute value function is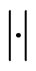 , then the three behaviors can be described as follows:
, then the three behaviors can be described as follows:
void AS_synergetic()
{
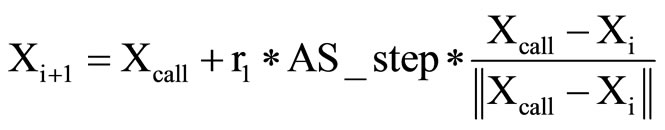 ;
;
};
void AS_reconnaissance()
{
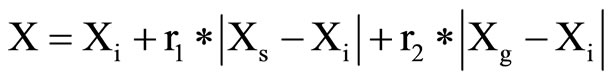 ;
;
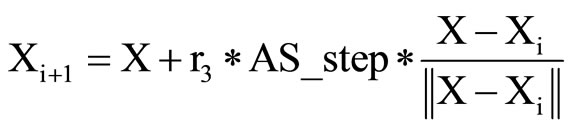 ;
;
}.
void AS_move ()
{
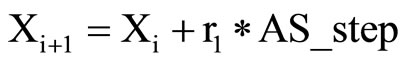 ;
;
};
4. Simulation and Performance Analysis
4.1. Simulation Functions
 (1)
(1)
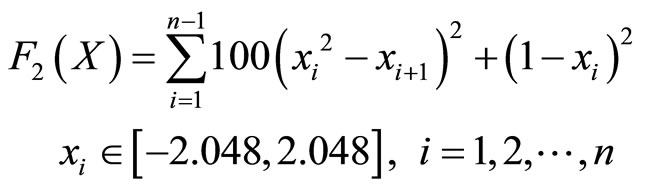 (2)
(2)
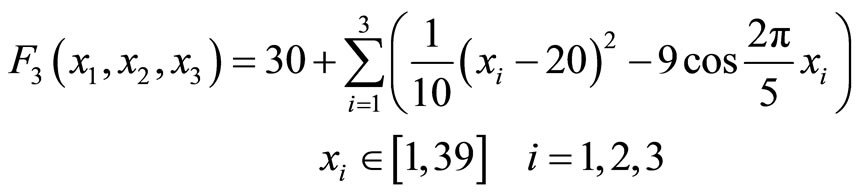 (3)
(3)
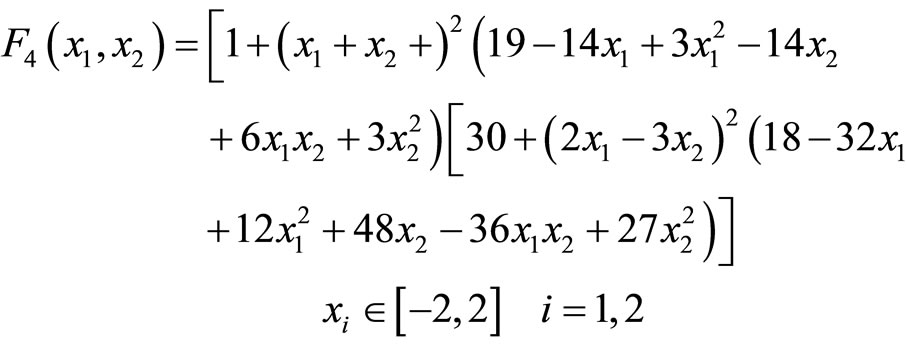 (4)
(4)
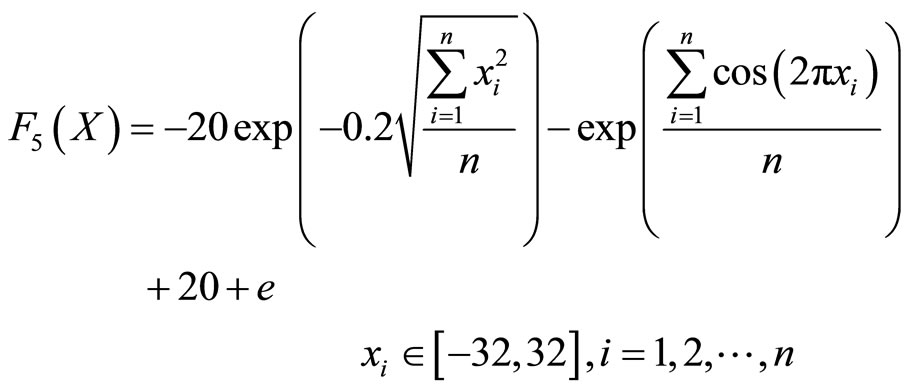 (5)
(5)
 (6)
(6)
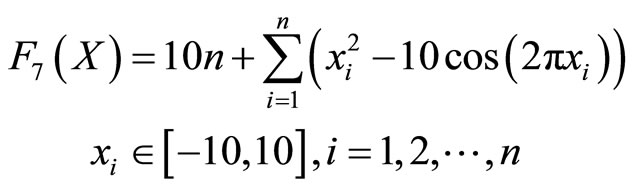 (7)
(7)
 (8)
(8)
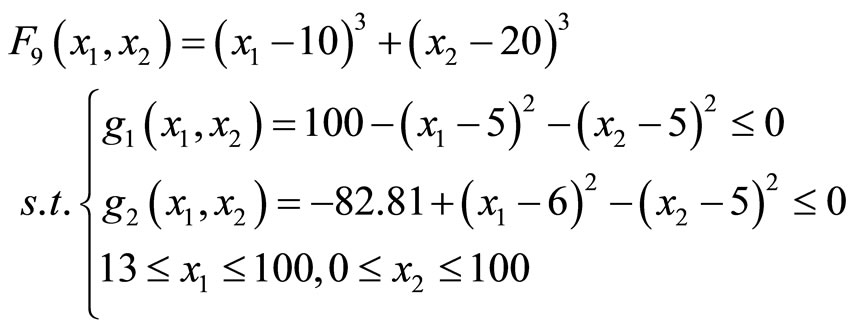 (9)
(9)
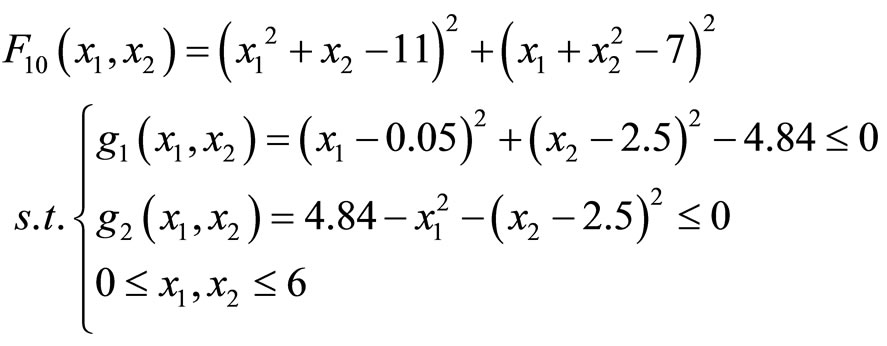 (10)
(10)
F1 has a global maximum 1 at point [0, 0], and a lot of local maximums distributed around it. The usual algorithms are easy to fall into local maximums or vibrate between the local minimum and maximum. It is often chosen to verify the validity of the algorithm.
F2 is the general Rosenbrock function. It has the global minimum value 0 at the points [1, 1, ···, 1]. As the global optimum is inside a long, narrow, parabolic shaped flat valley, it is difficult for global optimization, and often be used to detect the searching ability of algorithm.
F3 has a global minimum value 3 at point [20, 20, 20], and a lot of local minimum value distributed around it, it is a multi-variable function.
F4 is the Goldstein-Price function and has global minimum 3 at point [0, −1].
F5 is the Ackley’s Path function. It is a typical complex multidimensional multimodal function. It has the global minimum 0 at point [0, 0, ···, 0].
F6 is the Griewank function. It is a typical nonlinear multimodal function and has the extensive search space. It has the global minimum 0 at point [0, 0, ···, 0] and a lot of local minimums distributed around it. The number of local minimums relates to function’s dimension.
F7 is the Rastrigrin function. It has the global minimum 0 at point [0, 0, ···, 0].
F8 is the Step function. It has the global minimum 0 at point [0, 0, ···, 0].
F9 is a constrained optimization problem; it subjects to some constrained conditions. It has the minimum value −6961.81388 at point (14.095, 0.84296).
F10 is a constrained optimization problem. It has the minimum value 13.59084 at point (2.2468, 2.3818).
4.2. Performance Analysis and Comparison
ASSA is used to solve function F1. The size of the searching swarm is 10, searching step is 0.3, Pc is 0.006, and the number of iterations is 100. Figure 1 shows the initial distribution of searching swarm, the searching individuals distribute randomly in the region.
After 20 iterations, the distribution of swarm is shown in Figure 2. Some individuals have searched near the global optimum position.
After 50 iterations, the swarm distribution is shown in Figure 3. More individuals have searched near the global optimal solution.
As Figure 4 shown, after 100 iterations, most of the
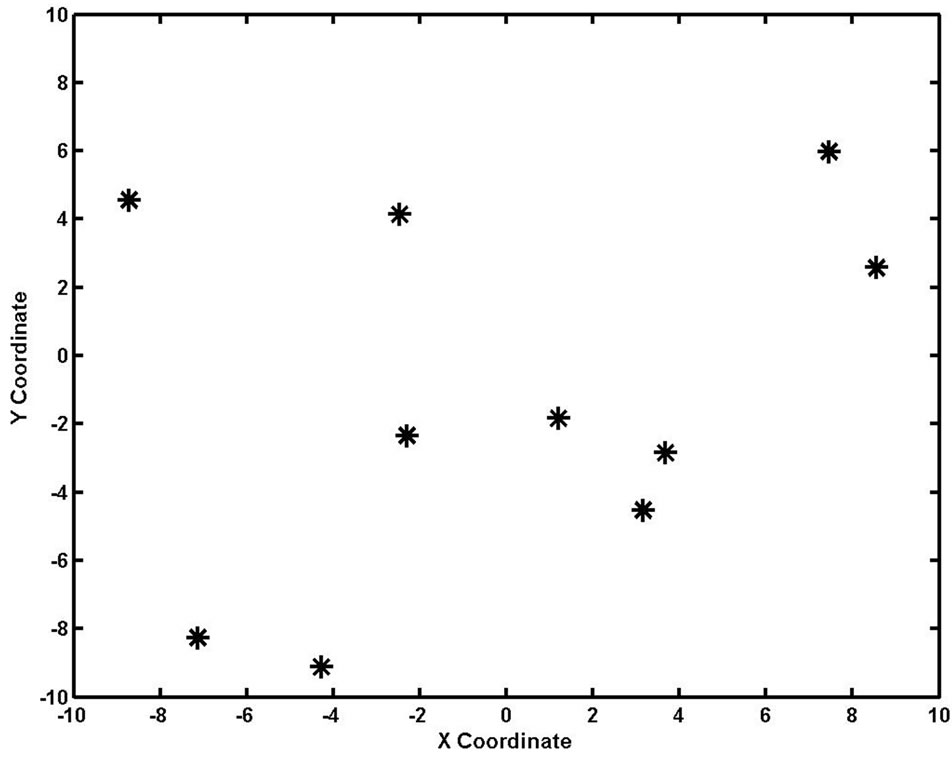
Figure 1. Distribution of the initial swarm.
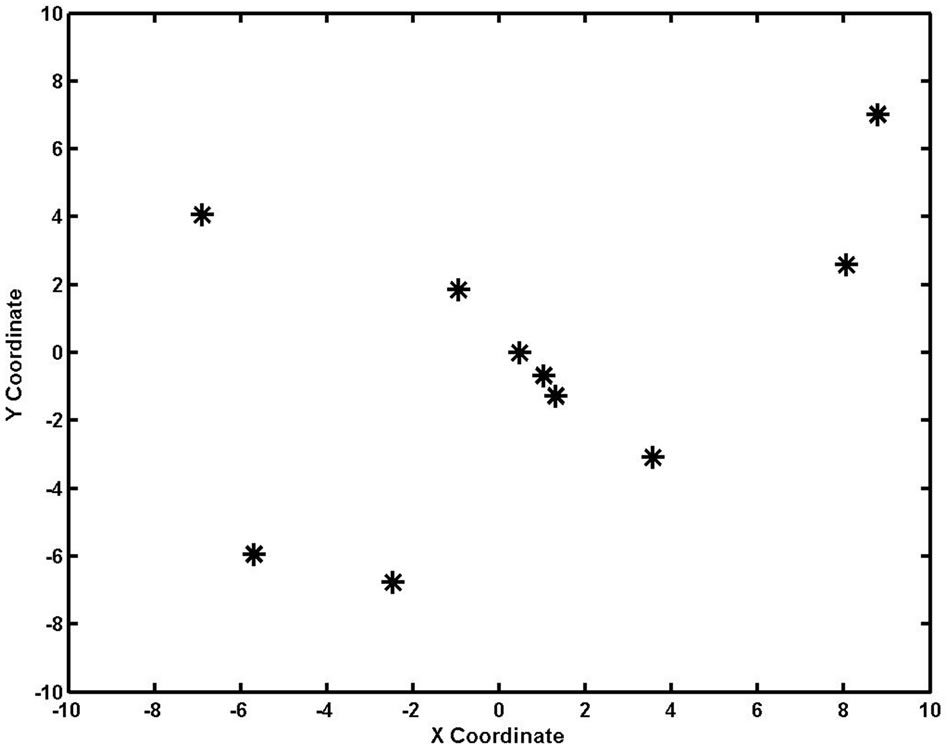
Figure 2. Distribution of the swarm after 20 iterations.
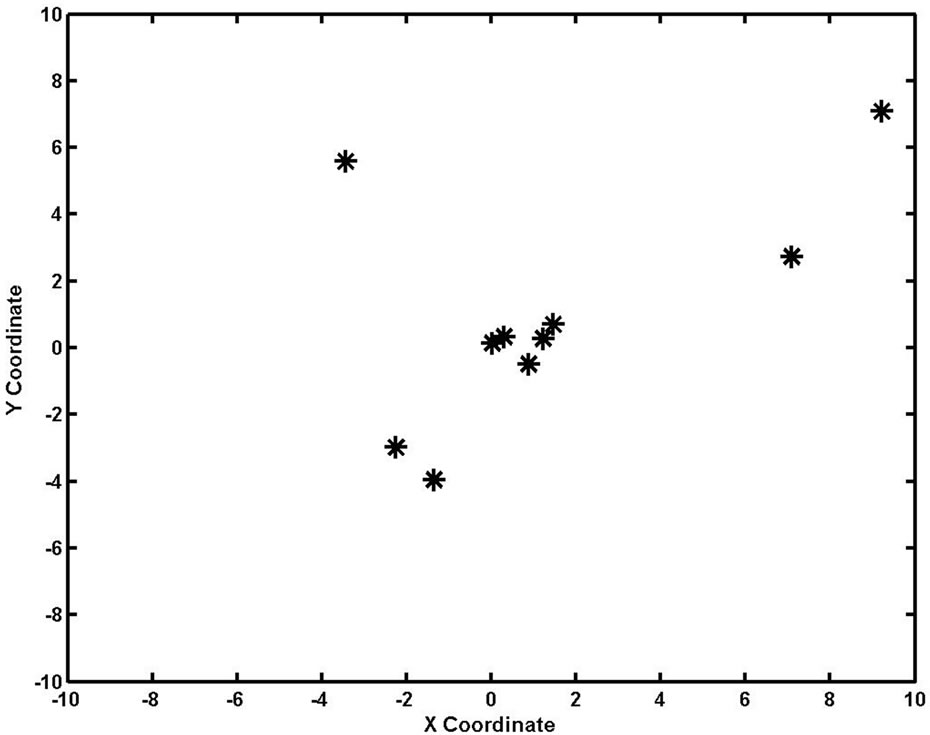
Figure 3. Distribution of the swarm after 50 iterations.
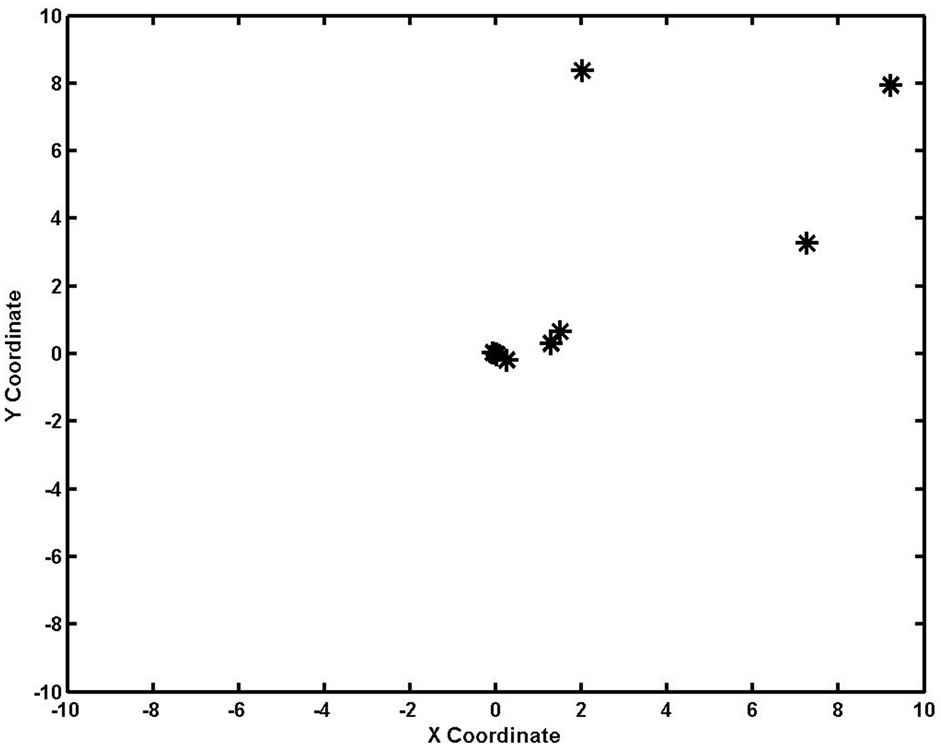
Figure 4. Distribution of the swarm after 100 iterations.
individuals have searched near the optimal solution, and the value of the best individual is getting closer and closer to the optimal value, that concretely shows the effecttiveness of the algorithm.
In order to describe the process of the searching swarm hunting for the optimal solution concretely, Figure 5 shows the change track of the best individual’s fitness value intercepted from the 34th to 100th iteration. ASSA shows a powerful searching ability, and goes forward to the optimal solution all along. The value of the best individual is more and more approaching to the optimal value that reflects a better searching ability and searching efficiency of the ASSA.
ASSA and GA are used respectively to solve function F2. Select n is 3, the swarm size is 10, searching step is 0.2, Pc is 0.002, and the iteration is 100. The GA uses binary code, the crossover probability is 0.6, mutation probability is 0.001, and the length of binary code is 30. The test results are shown in Figure 6. In the early running time, because of the restriction of the searching step,
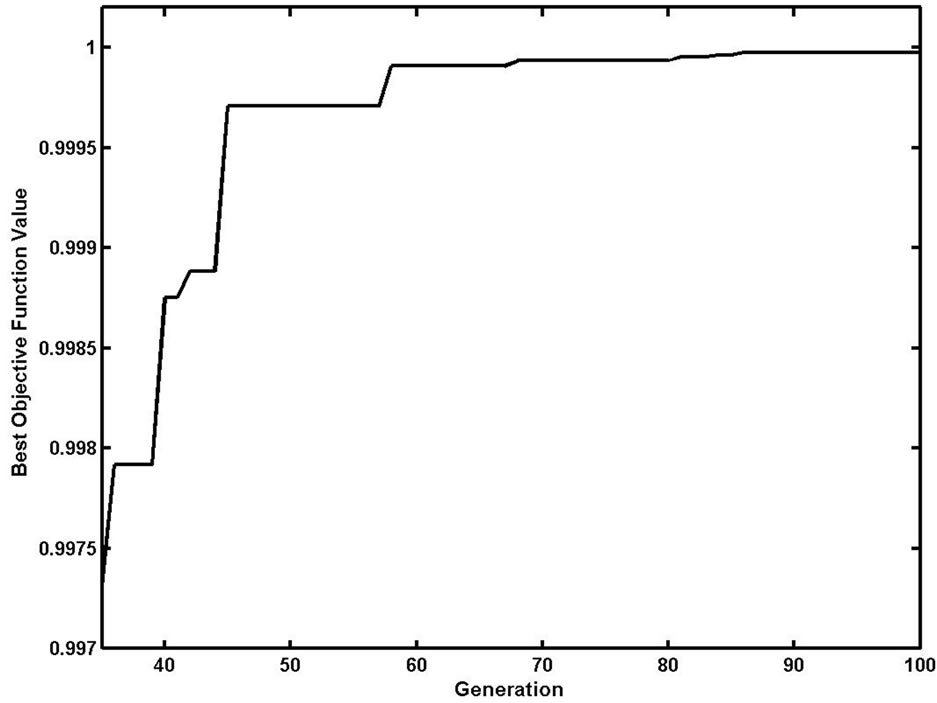
Figure 5. Latter part of the objective function value of the best individual.
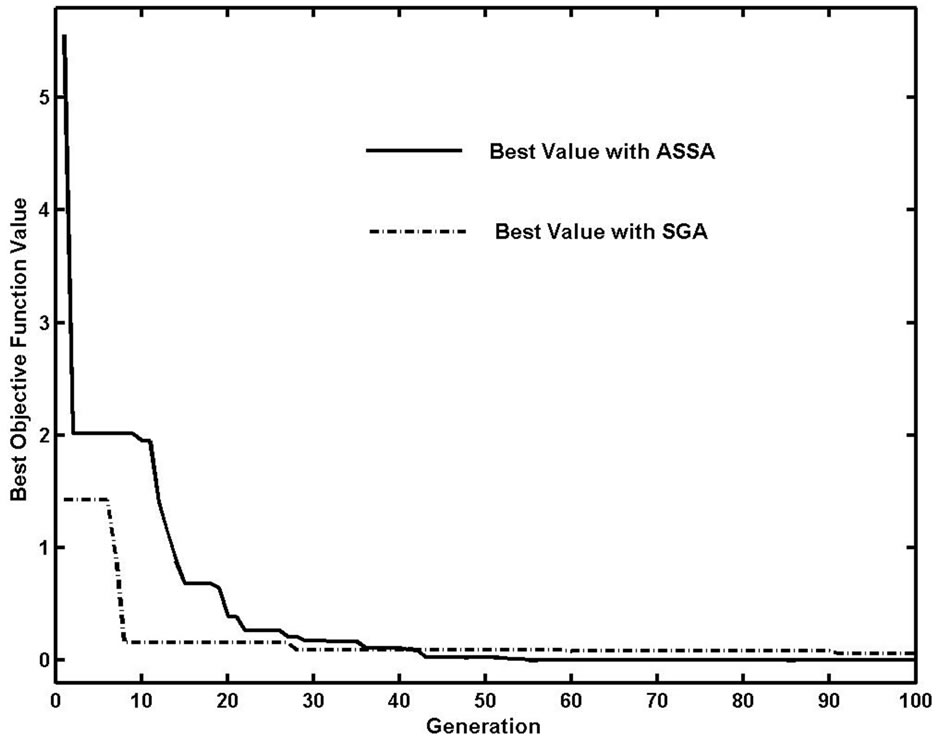
Figure 6. Comparison of the best individual value of ASSA and SGA.
the ASSA is slower than the GA, but ASSA exceeds the GA and gets the better optimization results finally.
In order to compare the performance of ASSA and PSO, function F4 is selected to do simulation experiment. The swarm size is 10, Pc is 0.02, iteration is 100, searching step of ASSA is 0.6, the inertia weight of PSO is descending, experiments are 100 times, and the results are shown in Figure 7. ASSA has better performance than PSO besides several running cases.
AFSA is a new intelligent optimization algorithm based on the simulation of the fish behaviors. Function F3 is selected to do simulative experiment with ASSA and AFSA respectively. The Swarm size is 100, Pc is 0.006, iteration is 100, searching step of ASSA and AFSA are 0.6, the fish vision of AFSA is 15, and experiments are 100 times. The results are shown as Figure 8. ASSA has better holistic performance than AFSA.
For testing the searching ability of ASSA in high dimension space function F5, F6, F7 and F8 are selected to do experiment respectively. The dimension is 20, swarm size is 30, the number of iteration is 50, experiments are 50 times, searching step of F5 is 9, searching step of F6 is 150, searching step of F7 is 5.5 searching step of F8 is 40, Pc is 0.006, and the results are shown as Table 1.
The change track of the best individual’s fitness value of F5, F6 are shown as Figures 9 and 10 respectively.
From the results ASSA has the better performance in

Figure 7. Comparison of the best individual value of ASSA and PSO.
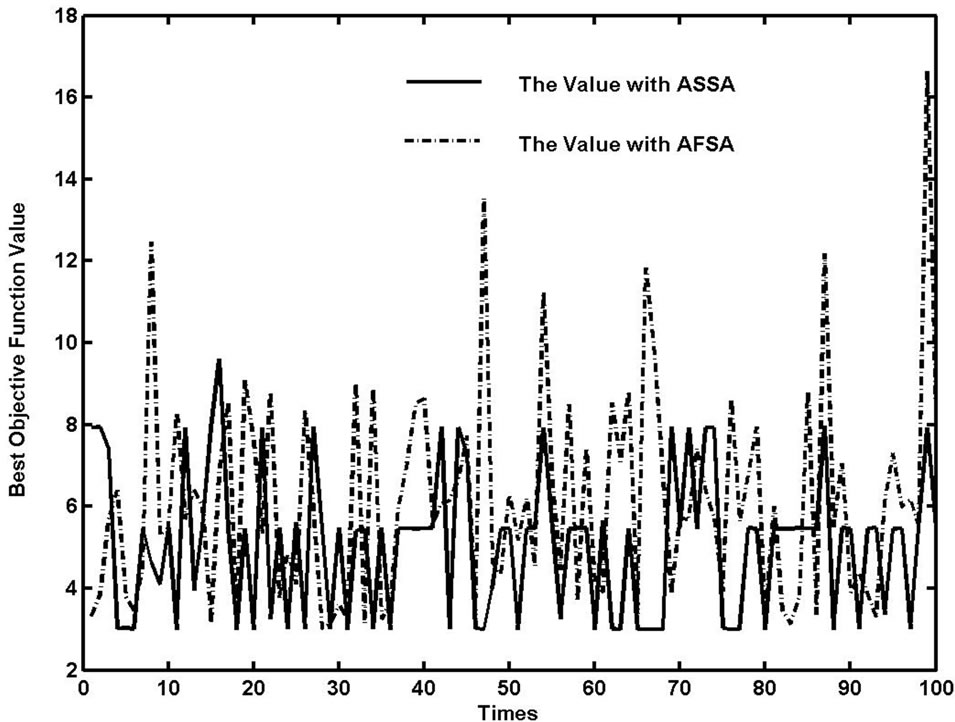
Figure 8. Comparison of the best individual value of ASSA and AFSA.
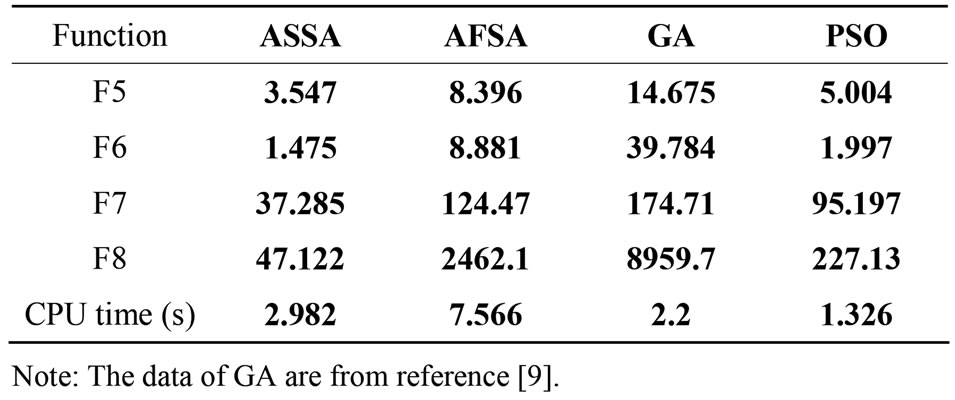
Table 1. Optimal value of algorithms.
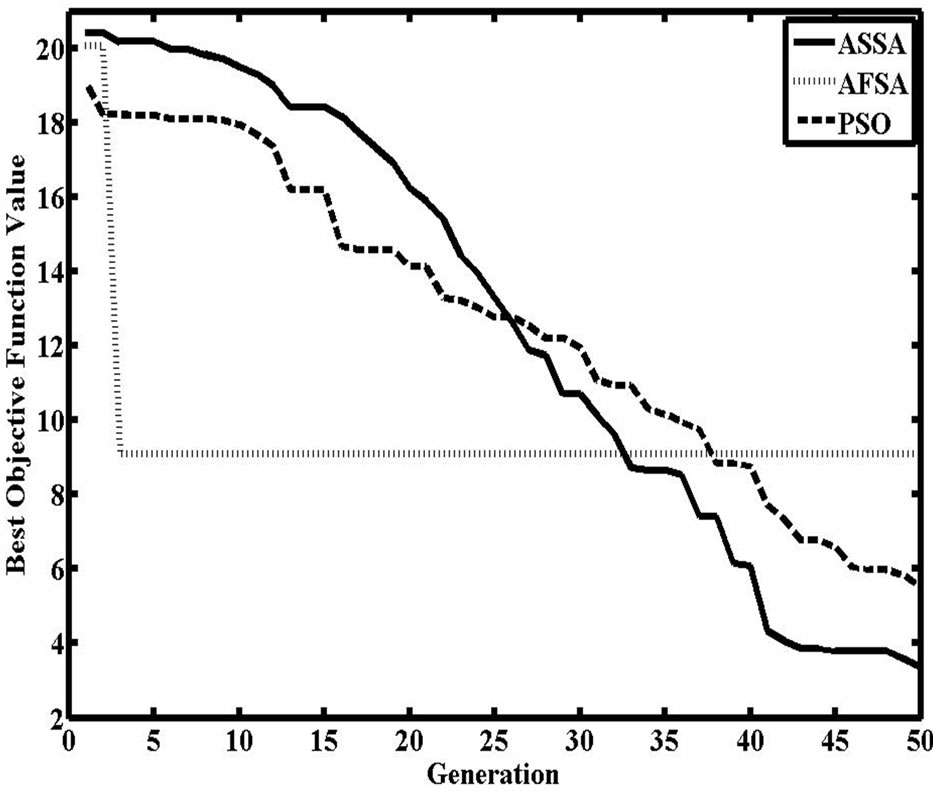
Figure 9. Comparison of the best individual value of F5.
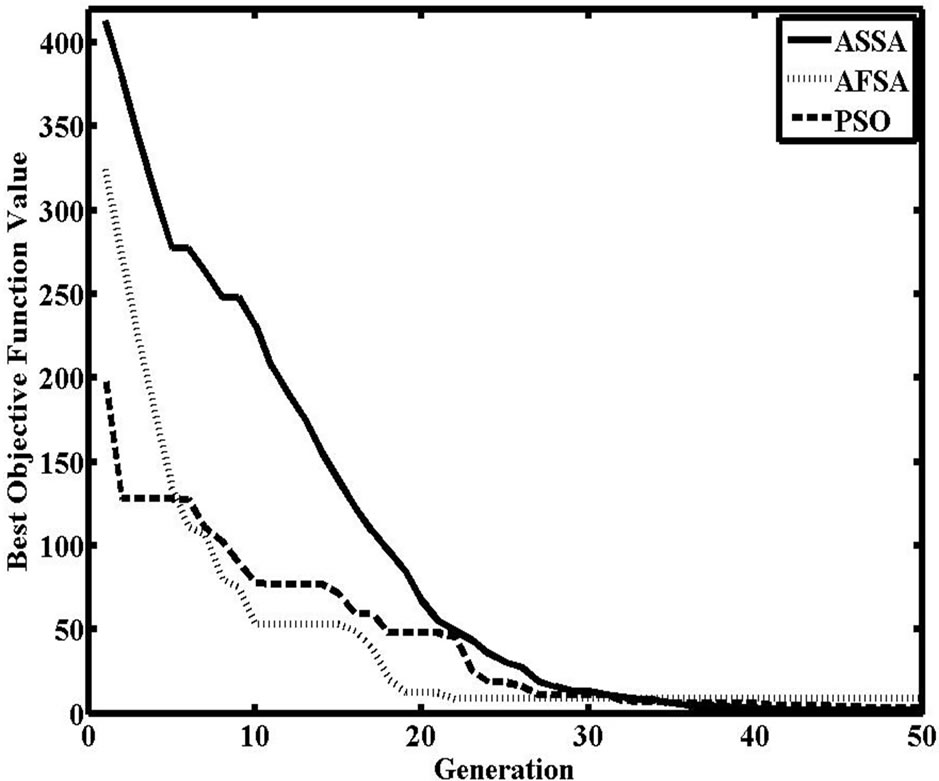
Figure 10. Comparison of the best individual value of F6.
high dimension optimization, but does not behaves outstanding ability in running time. Having more move rules may be the main reason.
4.3. Experiments for Solving Constrained Optimization Problems
For solving the constraint optimization problem, Penalty Function Method (PFM) is a useful method. Penalty function method converts the object function into the penalty function which included the constrained information, and the process of solving constraint optimization problem is transformed to the process of continuously solving unrestraint optimization problem.
Penalty function method has the penalty factor sequence which makes difficulty to program. The penalty factor (has fixed value) usually be used for simple.
About function F9, with PFM, select swarm size is 100, the number of iteration is 500, searching step = 0.6, experiment times = 10, and the penalty factor = 108. The results are shown as Table 2.
About function F10, with PFM, select swarm size is 200, the number of iteration is 500, searching step = 0.2, experiment times = 10, and the penalty factor = 108. The results are shown as Table 3.
From simulative results ASSA is an effective algorithm for solving constrained optimization problems.
4.4. Parameter Analysis and Comparison
According to the synergetic move rule, the value of synergetic parameter is a key factor that restrains local convergence and influences the performance of ASSA.
For verifying the analysis above, function F1 is selected to do the simulation tests. The swarm size is 10, searching step is 0.3, the number of iteration is 100, and the results are shown as Figure 11.
From the results selecting the value of synergetic parameter properly can enhance the performance of ASSA. The value of the probability is suggested between 0.001 - 0.1.
Searching step is one of the main factors which affect the performance of ASSA. Select function F3, the population size is 100, Pc is 0.006, the half length of the searching area as the initial vale of the searching step, which gradually decreases as the algorithm running. The results are shown as Figure 12.
From the results, the larger searching step the swarm move faster in the early running of the algorithm, but the algorithm losses the continual searching capability in the latter running time; if searching step is smaller, the moving of the swarm is slower, although it can continue searching in the latter running time, it can’t get better results for constraints of the iterative number. According to the simulation results, the more satisfactory results of searching step are between 15% - 30% length of the searching area.

Table 2. Results of function F9.
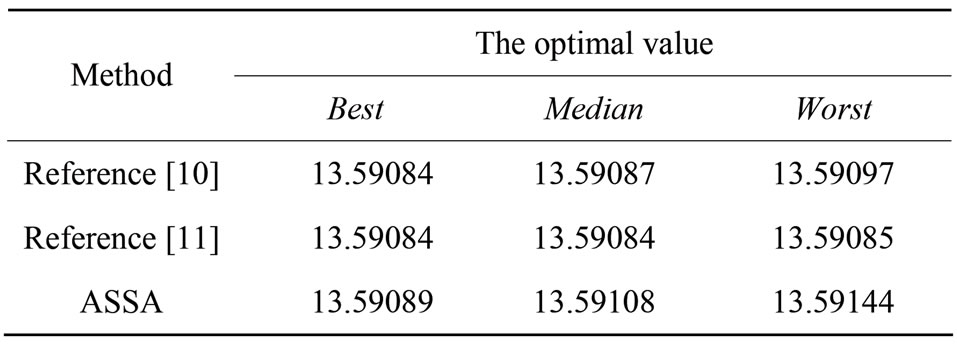
Table 3. Results of function F10.
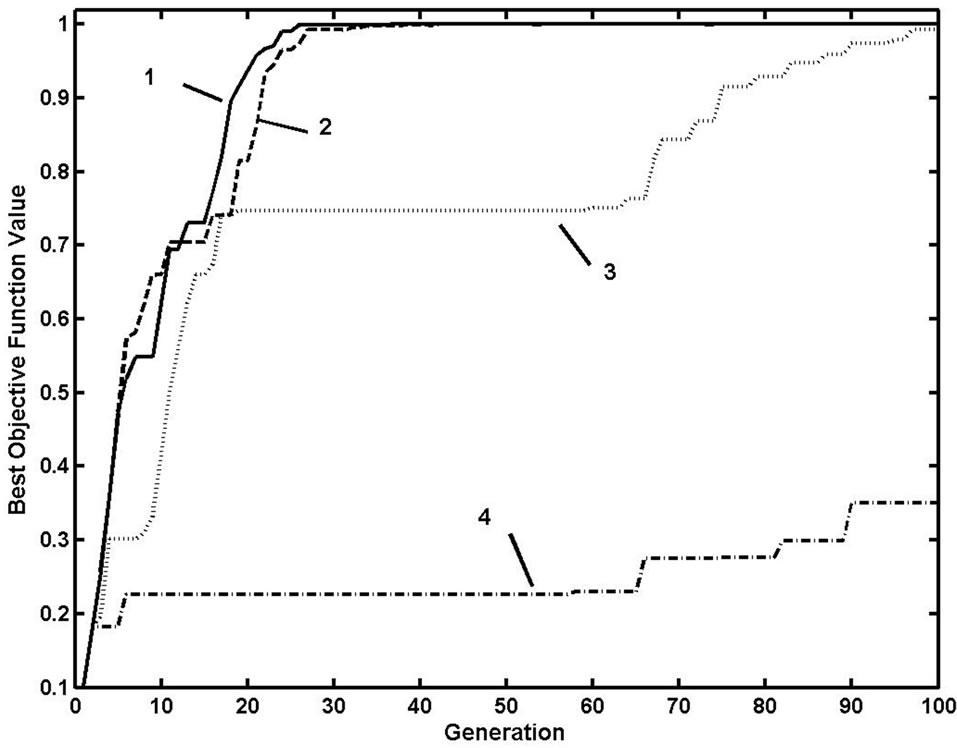
Figure 11. Comparative results with different value of Pc (1: Pc = 0.002, 2: Pc = 0.02, 3: Pc = 0.2, 4: Pc = 1.0 ).
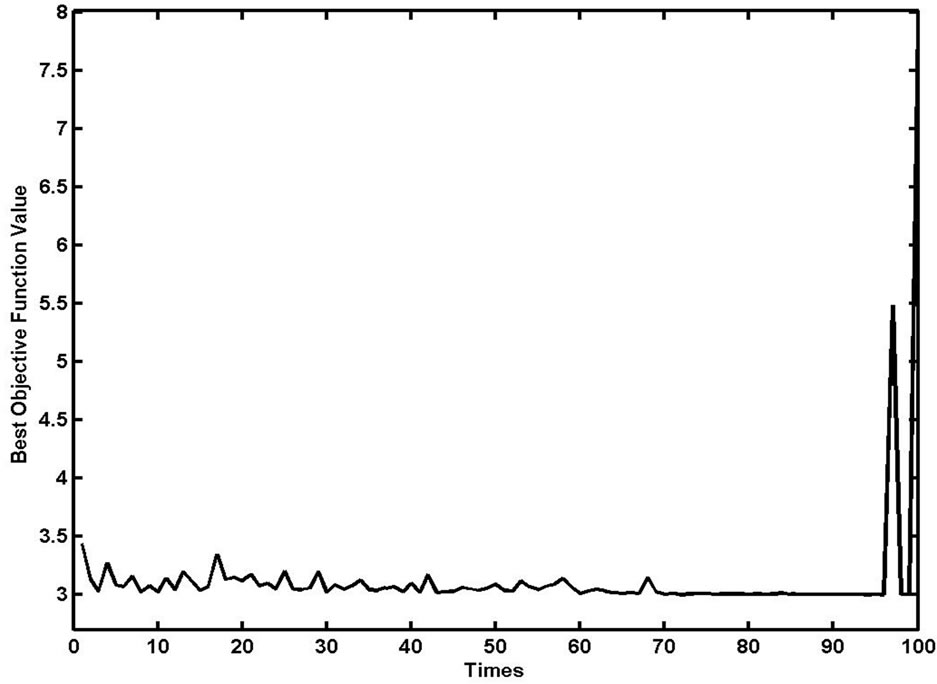
Figure 12. Influence of searching step.
As well known the population size is a key factor influenced the performance of BIOA. In general, the larger the population, the better the performance, but it does not meet the linear relationship. For ASSA the advisable value of the population size is suggested between 10 - 200.
5. Conclusions
Artificial Searching Swarm Algorithm (ASSA) is based on the simulation of the operation principle and abstract model of BIOA. In ASSA, the process of solving optimization problem is transformed into the process of searching optimal goal by searching swarm with set rules, and the optimal solution is found through the search and cooperation of the searching individuals.
ASSA possesses easy programmable, simple structure, insensitive to initial values, strong global searching ability, and small swarm running ability character. The algorithm is used for optimizing multivariable functions and the results produced by ASSA, Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Artificial FishSwarm Algorithm (AFSA) have been compared. The experiment results showed that ASSA is an effective optimization algorithm.
6. Acknowledgements
This work was supported by the Natural Science Foundation of Hebei Province under Grant No. E2011202040.
REFERENCES
- J. H Holland “Adaptation in Nature and Artificial System,” MIT Press, Cambridge, 1992.
- M. Dorigo, “Optimization, Learning and Natural Algorithms,” Ph.D. Thesis, Department of Electronics, Polytechnic of Milan, Milan, 1992.
- J. Kennedy and R. C. Eberhart, “Particle Swarm Optimization,” Proceedings of the IEEE International Conference on Neural Networks, Perth, 27 November-1 December 1995, pp. 1942-1948. doi:10.1109/ICNN.1995.488968
- X. L. Li, Z. J. Shao and J. X. Qian, “An Optimization Method Based on Autonomous Animats: Fish-Swarm Algorithm,” Systems Engineering-Theory & Practice, Vol. 22, No. 11, 2002, pp. 32-38.
- M. Eusuffm and K. E. Lansey, “Optimization of Water Distribution Network Design Using Shuffled Frog Leaping Algorithm,” Journal of Water Resources Planning and Management, Vol. 129, No. 3, 2003, pp. 210-225. doi:10.1061/(ASCE)0733-9496(2003)129:3(210)
- T. G. Chen, “A Simulative Bionic Intelligent Optimization Algorithm: Artificial Searing Swarm Algorithm and its performance Analysis,” Proceedings of the Second International Joint Conference on Computational Sciences and Optimization, Sanya, Hainan, 24-26 April 2009, Vol. 2, pp. 864-866. doi:10.1109/CSO.2009.183
- H. B. Duan, D. B. Wang and X. F. Yu, “Research on some Novel Bionic Optimization Algorithms,” Computer Simulation, Vol. 24, No. 3, 2007, pp.169-172.
- H. Wang and F. Qian, “Swarm Intelligent Optimization Algorithms,” Chemical Automation and Instrumentation, Vol. 34, No. 5, 2007, pp.7-13.
- H. P. Ma, H. Li and X. Y. Run, “Species Migration-Based Optimization Algorithm and Performance Analysis,” Control Theory & Applications, Vol. 27, No. 3, 2010, pp. 329-334.
- X. H. Wang, X. M. Zheng and J. M. Xiao, “Artificial Fish-Swarm Algorithm for Solving Constrained Optimization Problems,” Computer Engineering and Applications, Vol. 43, No. 3, 2007, pp. 40-42.
- Y. R. Zhou, J. X. Zhou and Y. Wang, “An Optimised Evolutionary Algorithms for Nonparameter Penalty Function,” Computer Engineering, Vol. 31, No. 10, 2005, pp. 31-33.

