Journal of Applied Mathematics and Physics
Vol.2 No.7(2014), Article
ID:47227,14
pages
DOI:10.4236/jamp.2014.27080
Simplex Optimization and Its Applicability for Solving Analytical Problems
Anna Maria Michałowska-Kaczmarczyk1, Tadeusz Michałowski2*
1Department of Oncology, The University Hospital in Cracow, Cracow, Poland
2Faculty of Engineering and Chemical Technology, Cracow University of Technology, Cracow, Poland
Email: *michalot@o2.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 April 2014; revised 14 May 2014; accepted 21 May 2014
ABSTRACT
Formulation of the simplex matrix referred to n-D space, is presented in terms of the scalar product of vectors, known from elementary algebra. The principles of a simplex optimization procedure are presented on a simple example, with use of a target function taken as a criterion of optimization, where accuracy and precision are treated equally in searching optimal conditions of a gravimetric analysis.
Keywords:Simplex, Simplex Optimization Procedure

1. Introduction
Simplex is a geometric figure, formed on the basis of  points
points  in the n-dimensional space, i.e., a number of the points exceeds the dimension of the space by one. These points are referred to as the vertices of the simplex. Distribution of the points
in the n-dimensional space, i.e., a number of the points exceeds the dimension of the space by one. These points are referred to as the vertices of the simplex. Distribution of the points  in this space is represented by a matrix of this simplex. Specifying the coordinates for
in this space is represented by a matrix of this simplex. Specifying the coordinates for 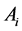 is easy if it concerns the
is easy if it concerns the  or
or  space, but it becomes less comprehensible when the issue concerns the n-dimensional
space, but it becomes less comprehensible when the issue concerns the n-dimensional  simplex. Although in the literature [1] one can find ready-made forms of the simplex matrix in
simplex. Although in the literature [1] one can find ready-made forms of the simplex matrix in 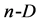 space, but information on how to receive it in an easy manner is lacking.
space, but information on how to receive it in an easy manner is lacking.
The simplex concept is the basis for the Nelder-Mead [2] simplex optimization procedure (SOP) [3] , conceived as a modification of the simplex method of Spendley, Hext and Himsworth [4] . The SOP is easy to use, and does not require calculation of derivatives [5] [6] , as in the gradient (local steepest descent) method [7] [8] ). The SOP is widely applicable and popular in different fields of chemistry, chemical engineering, and medicine [9] . Furthermore, it works well in practice on a wide variety of problems, where real-valued minimization functions with scalar variables are applied.
The sequential simplex method is considered as one of the most effective and robust methods applied in methodology of Evolutionary Operation (EVOP) experimental design [10] -[15] . The SOP method was implemented in MINUIT (a Fortran from CERN [16] package), then in Pascal, Modula-2, Visual Basic, and  [17] . The iterations are stopped when the function minimized is less than a preset value.
[17] . The iterations are stopped when the function minimized is less than a preset value.
In this article, the problem of obtaining the simplex matrix in 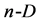 space will be presented on the basis of the triangle and the scalar product concept, well-known to the students from earlier stages of education. The evolution of the simplex according to SOP [3] [18] will also be presented in a understandable manner.
space will be presented on the basis of the triangle and the scalar product concept, well-known to the students from earlier stages of education. The evolution of the simplex according to SOP [3] [18] will also be presented in a understandable manner.
2. Simplexes in 2-D and 3-D Space
In order to introduce the simplex concept, we start from the point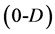 , (I) segment
, (I) segment , (II) equilateral triangle
, (II) equilateral triangle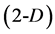 , and (III) tetrahedron
, and (III) tetrahedron 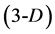 concepts, known from the elementary geometry. The
concepts, known from the elementary geometry. The ,
,  ,
, 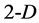 ,
, 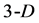 (and generally
(and generally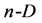 ) notations express the dimensionality of the corresponding geometrical entities (Figure 1).
) notations express the dimensionality of the corresponding geometrical entities (Figure 1).
The points: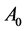 ,
,  ,
,  are vertices of the triangle
are vertices of the triangle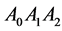 ; the points:
; the points: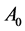 ,
, 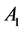 ,
,  ,
,  are the vertices of the tetrahedron
are the vertices of the tetrahedron .
.  is one of the edges of the triangle;
is one of the edges of the triangle; 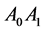 is one of the edges of the tetrahedron. Equilateral triangle
is one of the edges of the tetrahedron. Equilateral triangle  is one of walls of the tetrahedron.
is one of walls of the tetrahedron.
Segment, equilateral triangle, and tetrahedron can be presented in the same scale; it means that all distances, equal to unity (chosen arbitrarily), between the (neighbouring) points  and
and  of a polygon are assumed, i.e. the length
of a polygon are assumed, i.e. the length .
.
All angles between edges of the equilateral triangle are equal to 60˚ . All angles between adjacent tetrahedron edges are equal 60˚ too, owing to the fact that all the tetrahedron walls are composed of equilateral triangles
. All angles between adjacent tetrahedron edges are equal 60˚ too, owing to the fact that all the tetrahedron walls are composed of equilateral triangles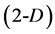 . By turns, tetrahedrons form the
. By turns, tetrahedrons form the 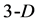 walls in
walls in 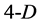 polygon, etc. It means that all angles between adjacent edges of a symmetrical
polygon, etc. It means that all angles between adjacent edges of a symmetrical  polygon are equal 60˚, as well.
polygon are equal 60˚, as well.
The equilateral triangle can assume different positions on the plane. A particular case is the triangle with unit edges, “anchored” at the origin of co-ordinate axis, as one presented in Figure 2.
The successive vertices of the equilateral triangle can be presented in matrix form, where the rows are expressed by co-ordinates of the corresponding points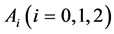 :
:
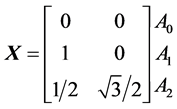 (1)
(1)
The second and third rows of this matrix are identical with components of transposed vectors:  and
and , respectively:
, respectively:

The tetrahedron can assume different positions in  space. A particular case is the tetrahedron anchored at the origin of co-ordinate axis as one presented in Figure 3.
space. A particular case is the tetrahedron anchored at the origin of co-ordinate axis as one presented in Figure 3.
The successive vertices of the tetrahedron can be presented in the matrix form:
 (2)
(2)
The second, third and fourth rows of this matrix are identical with components of the transposed vectors: ,
, 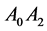 and
and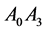 , respectively:
, respectively:


Figure 1. Equilateral triangle and tetrahedron.

Figure 2. The equilateral triangle with unit edges and points: ;
;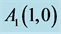 ;
;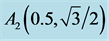 .
.

Figure 3. The tetrahedron with unit edges and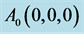 ;
;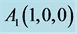 ;
; ;
;  .
.
3. Simplexes in n-D Space
The segment, equilateral triangle and tetrahedron are imaginable concepts. However, application of the concepts involved with geometric figures of higher dimension  is beyond imagination. One should be taken into account that, in the simplex optimization, we are forced, as a rule, to consider higher number of factors influencing the optimizing process.
is beyond imagination. One should be taken into account that, in the simplex optimization, we are forced, as a rule, to consider higher number of factors influencing the optimizing process.
Although the figures in  space (Cartesian co-ordinate system) are beyond imagination, one can present them in projective space. In Figure 4, any pair of points of the simplex is connected, informally, by a segment (line); the segments (sides, edges) are marked there with broken lines. Particularly, two points form the
space (Cartesian co-ordinate system) are beyond imagination, one can present them in projective space. In Figure 4, any pair of points of the simplex is connected, informally, by a segment (line); the segments (sides, edges) are marked there with broken lines. Particularly, two points form the  simplex in
simplex in  space. Adding a third point (that not lies along the segment or its extension) gives a triangle (
space. Adding a third point (that not lies along the segment or its extension) gives a triangle ( simplex) in
simplex) in 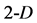 space. Adding a fourth point in
space. Adding a fourth point in 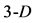 space (not coplanar with
space (not coplanar with  simplex plane), one obtains a tetrahedron (
simplex plane), one obtains a tetrahedron (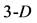 simplex), etc. Generally, adding a successive
simplex), etc. Generally, adding a successive  -th
-th 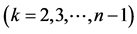 point, do not lying in surface formed by
point, do not lying in surface formed by 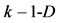 simplex, one obtains the
simplex, one obtains the 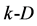 simplex. In other words, adding the successive point that not lies on (or in plane of) simplexes of lower dimension and connecting it, every time, with the remaining points, one can imagine the simplexes with larger and larger dimensions, in projective space.
simplex. In other words, adding the successive point that not lies on (or in plane of) simplexes of lower dimension and connecting it, every time, with the remaining points, one can imagine the simplexes with larger and larger dimensions, in projective space.

Figure 4. Formation of consecutive dimensions (up to ) of a simplex in projective space.
) of a simplex in projective space.
Let us assume that the polygon is “anchored” in n-D-space in such a manner that  is in the origin of the co-ordinate axis and any successive point “enters” the new dimension of the n-D-space, see Figure 4. It means that the co-ordinates of the corresponding points of
is in the origin of the co-ordinate axis and any successive point “enters” the new dimension of the n-D-space, see Figure 4. It means that the co-ordinates of the corresponding points of  polygon are as follows:
polygon are as follows:
 (3)
(3)
This means that  for
for .
.
As stated above, the number of vertices exceeds, by 1, the dimension of the space; it means that the polygon in  space involves
space involves 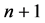 vertices.
vertices.
We consider a pencil of n unit vectors,  , all starting from the point
, all starting from the point
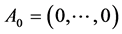 , i.e., origin of co-ordinates of
, i.e., origin of co-ordinates of 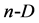 space and ending at the points
space and ending at the points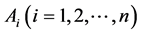 . One should notice that the basic components
. One should notice that the basic components 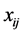 of the vector
of the vector  starting at the origin of co-ordinates, are identical with co-ordinates of the point
starting at the origin of co-ordinates, are identical with co-ordinates of the point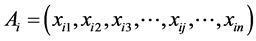 . Then for the vectors
. Then for the vectors  based on the points specified in (3) we have:
based on the points specified in (3) we have:
 (4)
(4)
Let us construct the matrix  (Equation (5)) composed of the co-ordinates of the corresponding points in
(Equation (5)) composed of the co-ordinates of the corresponding points in  space:
space:
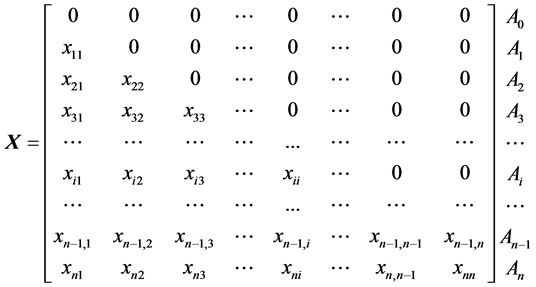 (5)
(5)
Moreover, we assume non-negative values for the coordinates, i.e. , and then the elements of the matrix
, and then the elements of the matrix 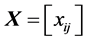 can be specified as follows:
can be specified as follows:
 (6)
(6)
Let  be the unit vector along the i-th axis, Xi, i.e.
be the unit vector along the i-th axis, Xi, i.e.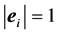 . The
. The  vectors form a set of mutually orthogonal vectors in
vectors form a set of mutually orthogonal vectors in  space. The scalar products:
space. The scalar products:
 (7)
(7)
where 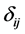 is the Kronecker symbol.
is the Kronecker symbol.
Any vector  in
in 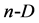 space can be also written as
space can be also written as ;
;  . Then the scalar product of two vectors,
. Then the scalar product of two vectors, 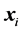 and
and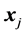 , in
, in 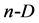 space is as follows:
space is as follows:
 (8)
(8)
where  is the angle between vectors
is the angle between vectors  and
and  spanning the simplex in
spanning the simplex in 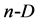 space. The angle between different vectors
space. The angle between different vectors 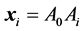 and
and  of
of 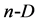 simplex equals
simplex equals 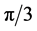 [rd], i.e.
[rd], i.e. 
and then , for any pair of the vectors
, for any pair of the vectors 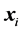 and
and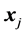 : in triangle
: in triangle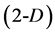 , in tetrahedron
, in tetrahedron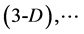 . Moreover,
. Moreover,  and then
and then . If the unit vectors
. If the unit vectors 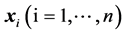
are assumed, i.e., 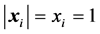 , then from (8) and (4)-(6) we have:
, then from (8) and (4)-(6) we have:
 (9)
(9)
 (10)
(10)
From (9), (10) and (6) we get, by turns,
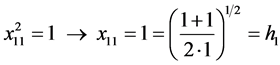
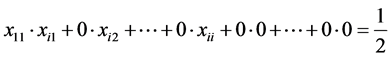 , i.e.
, i.e.


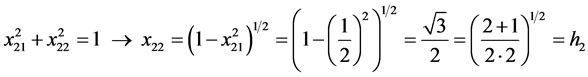
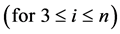

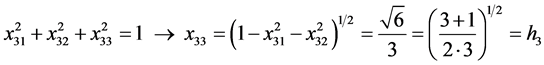




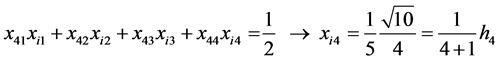
and so forth. On this basis, one can write:
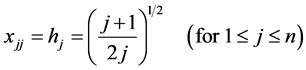 (11)
(11)
 (12)
(12)
The elements  of the matrix
of the matrix  (Equation (5)) are thus derived with use of principles of elementary algebra and geometry. Then the
(Equation (5)) are thus derived with use of principles of elementary algebra and geometry. Then the  simplex can be written in the form
simplex can be written in the form
 (13)
(13)
One can notice that hj (Equation (15)) is the height of  symmetrical simplex and
symmetrical simplex and 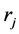 (Equation (16)) is the radius of
(Equation (16)) is the radius of  sphere (for
sphere (for —circle, for
—circle, for —“normal” sphere) inscribed in
—“normal” sphere) inscribed in  simplex. Moreover, we have the relations:
simplex. Moreover, we have the relations:
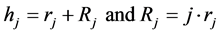 (14)
(14)
where Rj is the radius of  sphere circumscribed on
sphere circumscribed on 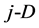 simplex, see Figure 5.
simplex, see Figure 5.
In particular, for , the matrix
, the matrix  (Equation (13)) has 7 columns and 8 rows.
(Equation (13)) has 7 columns and 8 rows.
 (15)
(15)
4. Translation and Reflection of the Simplex
A simplex can be translated and/or rotated in space. Particularly, the simplex defined by  (Equation (13))with the centre at
(Equation (13))with the centre at , can be parallely shifted to the centre
, can be parallely shifted to the centre 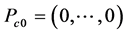 of the co-ordinate system. This way, one obtains a new matrix
of the co-ordinate system. This way, one obtains a new matrix 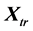
 (16)
(16)

Figure 5. Graphical presentation of ,
,  and
and  in
in  space (Equations (11) and (12)) for
space (Equations (11) and (12)) for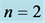 .
.
with 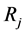 and
and 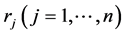 as ones in Equations (11), (12) and (14). Reflection of particular vertices of the matrix
as ones in Equations (11), (12) and (14). Reflection of particular vertices of the matrix 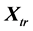 in the centre of co-ordinate system
in the centre of co-ordinate system 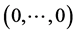 gives the simplex described by the matrix
gives the simplex described by the matrix
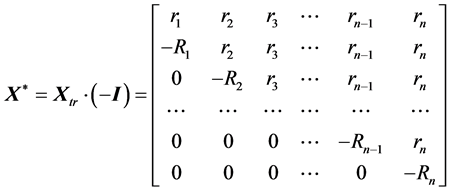 (17)
(17)
where —identity matrix.
—identity matrix.
The positions of the simplex presented in Figure 6 (in  space), obtained from (I) by translation (II) and mirror reflection (III) in the origin of ordinate axis, are presented by matrices:
space), obtained from (I) by translation (II) and mirror reflection (III) in the origin of ordinate axis, are presented by matrices:  and:
and:  (Equation (21) for
(Equation (21) for  and
and


Note that the number of  walls in
walls in  simplex equals to the number of
simplex equals to the number of  point subsets (
point subsets ( walls) generated from the
walls) generated from the 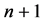 -point set. From the elementary theory of combinations it results that the number of k-D walls equals to the number of possible combinations of
-point set. From the elementary theory of combinations it results that the number of k-D walls equals to the number of possible combinations of  items taken
items taken 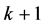 at a time, i.e.
at a time, i.e.
 (18)
(18)
Particularly, 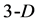 simplex (tetrahedron,
simplex (tetrahedron,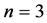 ) involves
) involves  triangles (
triangles (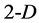 walls),
walls), 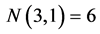 edges (segments, 1-D walls) and
edges (segments, 1-D walls) and 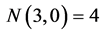 points (vertices,
points (vertices, 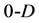 walls). Generally, the
walls). Generally, the  simplex consists of:
simplex consists of: 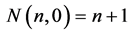 vertices of the virtual solid stretched on them,
vertices of the virtual solid stretched on them, 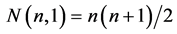 edges,
edges,  ,
, 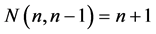 of
of  walls opposite to particular vertices.
walls opposite to particular vertices.
5. Simplex Optimization Procedure (SOP)
The simplex method, based on the simplex concept, is considered among the most efficient optimization procedures, successfully applied in different areas of optimization techniques and chemical analyses.The simplex concept is applicable, among others, for optimisation of analytical methods [13] , e.g. for searching the conditions

Figure 6. The simplexes obtained after successive (II) translation and (III) reflection of the original simplex (I) in the center of co-ordinate axes in  space; for details—see text.
space; for details—see text.
securing optimal accuracy and precision of an analytical method.
5.1. An Objective Function
The simplex concept is applicable, among others, for optimisation of analytical methods [13] . The variables,  (scalars), named as factors forming the vector
(scalars), named as factors forming the vector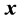 , affect the variable
, affect the variable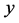 , named as objective (“target”) function, i.e.,
, named as objective (“target”) function, i.e.,
 (19)
(19)
The essence of optimisation is inherent in the objective function. Accuracy and precision are among the most important criteria of analytical methods. Another object functions are related to sensitivity of a method, efficiency of a chemical reaction, etc.
Let us assume that an analytical method aims to find the conditions securing true contents 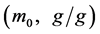 of an analyte in a sample to be obtained. For this purpose, the following criterion (objective function)
of an analyte in a sample to be obtained. For this purpose, the following criterion (objective function)
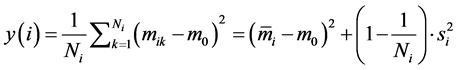 (20)
(20)
has been suggested [19] , where:
 (21)
(21)
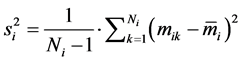 (22)
(22)
were calculated in the ![]() -th simplex point,
-th simplex point, 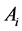 (Equation (3)), on the basis of
(Equation (3)), on the basis of  measurements
measurements 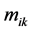 of an intensive variable
of an intensive variable 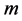 (e.g. number of grams of an analyte contained in a unit mass of solution);
(e.g. number of grams of an analyte contained in a unit mass of solution);  is the true value of this variable, obtained according to a reference method. In the object function (20), both terms, i.e. accuracy
is the true value of this variable, obtained according to a reference method. In the object function (20), both terms, i.e. accuracy 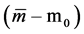 and precision, expressed by standard deviation,
and precision, expressed by standard deviation, 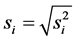 , are considered nearly equivalently; the difference in “weights”:
, are considered nearly equivalently; the difference in “weights”: ![]() and
and , of the two characteristics of the method becomes less significant at higher
, of the two characteristics of the method becomes less significant at higher  values.
values.
The function (20) is an example of superposition of different characteristics of a method, i.e. accuracy and precision. The optimisation is terminated when the systematic error is insignificant, i.e., the inequality
 (23)
(23)
is fulfilled; 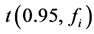 is the critical t-value of the Student’s t-test at
is the critical t-value of the Student’s t-test at  degrees of freedom, on
degrees of freedom, on 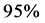 probability level pre-assumed. In particular, for
probability level pre-assumed. In particular, for , i.e.
, i.e. , we have
, we have , and then Equation (23) has the form
, and then Equation (23) has the form
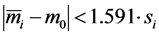 (24)
(24)
5.2. Decision Variables and Arrangement of Experimental Conditions
The optimization procedure assumes:
1) Selection of natural decision variables,  , as independent (in principle) individual factors affecting the values of the objective function (Equation (19)) and 2) Their order,
, as independent (in principle) individual factors affecting the values of the objective function (Equation (19)) and 2) Their order,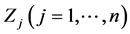 .
.
The number 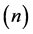 of the variables
of the variables 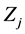 chosen defines the simplex dimension.
chosen defines the simplex dimension.
The kind  and the number
and the number 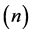 of these variables that assume continuous (not discrete) values
of these variables that assume continuous (not discrete) values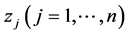 , consisting the vector
, consisting the vector , affects the success (efficiency) of optimisation process aiming to get optimal (maximal or minimal) value for the object function, e.g. minimal value for
, affects the success (efficiency) of optimisation process aiming to get optimal (maximal or minimal) value for the object function, e.g. minimal value for  defined by Equation (20). It should be noted that the
defined by Equation (20). It should be noted that the  simplex matrix (Equation (5)) refers—in principle—to orthogonal (independent) variables. The independent variables assuming continuous values are, among others: pH, temperature, time, rate of an operation.
simplex matrix (Equation (5)) refers—in principle—to orthogonal (independent) variables. The independent variables assuming continuous values are, among others: pH, temperature, time, rate of an operation.
One should be noticed that the form of the matrix (5) enables to add a new variable,  , to the set of n variables
, to the set of n variables 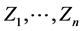 assumed at the start for optimization—provided that the decision of inclusion of variable
assumed at the start for optimization—provided that the decision of inclusion of variable  into the set of variables has been undertaken after measurements done in the points
into the set of variables has been undertaken after measurements done in the points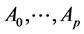 , at
, at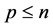 , where
, where 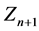 remained unchanged. In this case, the measurements done at the points
remained unchanged. In this case, the measurements done at the points  has not to be repeated.
has not to be repeated.
5.3. Design of Experiments and Optimization within the Starting Simplex
The introductory step of the optimization procedure assumes fixing the starting values,  , and steps,
, and steps, 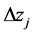 , assumed for
, assumed for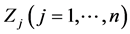 ; these values affect strongly the efficiency of the optimization procedure. Some constraints put on
; these values affect strongly the efficiency of the optimization procedure. Some constraints put on 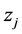 and
and  values (resulting from physicochemical, chemical or technological reasons) can also be taken into account. These constraints may result e.g., from limited solubility, possibility of phase change affected by temperature, etc.
values (resulting from physicochemical, chemical or technological reasons) can also be taken into account. These constraints may result e.g., from limited solubility, possibility of phase change affected by temperature, etc.
The optimization is realized there for values of natural variables calculated from the formula
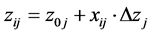 (25)
(25)
where  enumerates successive experimental points realized within the initial simplex. The advised values for
enumerates successive experimental points realized within the initial simplex. The advised values for  in (5) are defined in the matrix (13) and specified e.g. in the matrix (15) if
in (5) are defined in the matrix (13) and specified e.g. in the matrix (15) if . The values
. The values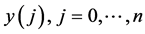 , obtained at
, obtained at 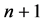 points
points  of the initial simplex are the basis for its further evolution of the simplex.
of the initial simplex are the basis for its further evolution of the simplex.
5.4. Optimization at the Points of Evolving Simplex
At the first stage of the simplex evolution (Figure 7), a point 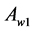 with the worst
with the worst  value,
value,  , for the object function (Equation (20)) is indicated,
, for the object function (Equation (20)) is indicated, . The point
. The point  is replaced by a new point,
is replaced by a new point,
 , obtained by reflection of
, obtained by reflection of 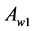 in the centre,
in the centre,  , of the remaining
, of the remaining  points of the initial simplexi.e., in
points of the initial simplexi.e., in 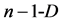 wall not containing the point
wall not containing the point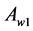 . In other words,
. In other words,  is the middle point between
is the middle point between  and
and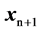 , i.e.,
, i.e.,
 (26)
(26)
After adding the term 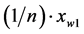 to both sides of Equation (26), we obtain the co-ordinates of the new point,
to both sides of Equation (26), we obtain the co-ordinates of the new point, 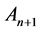 ,
,
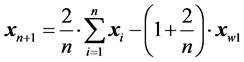 (27)
(27)
After measurement(s) done at the point , the values
, the values  are compared again within the new (evolved) simplex (containing
are compared again within the new (evolved) simplex (containing 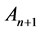 and not containing
and not containing ) and the point
) and the point 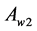 with the worst value,
with the worst value, 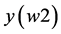 is chosen. Then
is chosen. Then  is reflected in the centre of
is reflected in the centre of 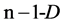 wall of the new simplex (not containing
wall of the new simplex (not containing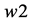 ). This way, a new point
). This way, a new point 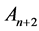 is obtained and further operations are repeated again, in cyclic manner. At
is obtained and further operations are repeated again, in cyclic manner. At  -th reflection one can write
-th reflection one can write
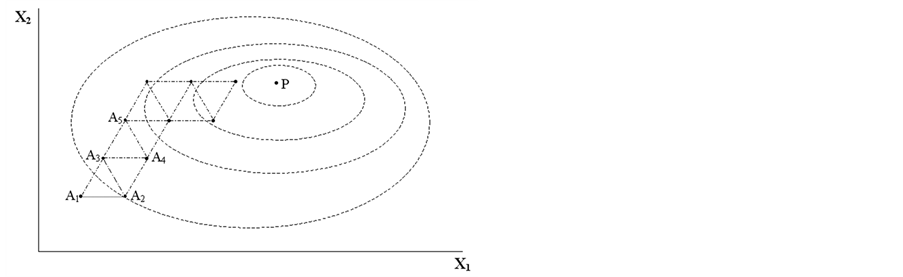
Figure 7. Evolving simplex in  space.
space.
 (28)
(28)
In the example presented above, the initial (symmetrical) shape of the evolving simplex is maintained owing to the fact that 1) mirror reflections are applied and 2) equal statistical weights are assumed to all the simplex points considered. Sometimes we are forced to move the simplex within a constrained component space [20] .
The evolving simplex approaches the quasi-optimal region, where  values do not change distinctly. In this region, the evolving simplex should be contracted or diminished (Figure 8); such operations enter e.g. the MINUIT program. The contraction/dilatation and weighting are involved in the relation [21] [22]
values do not change distinctly. In this region, the evolving simplex should be contracted or diminished (Figure 8); such operations enter e.g. the MINUIT program. The contraction/dilatation and weighting are involved in the relation [21] [22]
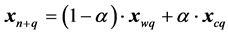 (29)
(29)
where the parameter α results from re-parametrization of the a line passing through 2 points: one of them is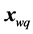 , the second one is the centre
, the second one is the centre  of area of
of area of 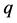 -th,
-th,  simplex, defined as follows
simplex, defined as follows
 (30)
(30)
where the operator means summation within
means summation within 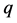 -th
-th 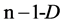 simplex (
simplex (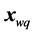 excluded). The contraction or expansion and weighting (“weights”
excluded). The contraction or expansion and weighting (“weights”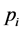 ) different points
) different points  deforms the evolving simplex gradually. As a rule, it is not an advantageous occurrence during the optimization procedure, however. The simplex deformation is influenced mainly by the weighting factors [23] . Moreover, a shape of response function may sometimes cause the optimum searching impossible, even in
deforms the evolving simplex gradually. As a rule, it is not an advantageous occurrence during the optimization procedure, however. The simplex deformation is influenced mainly by the weighting factors [23] . Moreover, a shape of response function may sometimes cause the optimum searching impossible, even in  space.
space.
6. Example of SOP
To illustrate the principle of SOP, a simple example of gravimetric analysis is considered below. The matrix expressed by Equation (15) was chosen for initial simplex, and Equation (20) was applied as criterion of optimization.  measurements were made at each simplex point. In our case, the relation (24) is chosen as the criterion of optimization. Analyses were made with CdSO4 solution of
measurements were made at each simplex point. In our case, the relation (24) is chosen as the criterion of optimization. Analyses were made with CdSO4 solution of , standardised according to electrogravimetry, considered as the reference method.
, standardised according to electrogravimetry, considered as the reference method.
6.1. Analytical Prescription
The samples, ca. 5 mL of the solution, weighed on analytical balance (±0.1 mg), were taken for analysis. The samples were treated with tartaric acid (0.220 g/mL) solution and then with 2.51 mol/L NaOH solution. After dilution with water, the solution was treated with 8-hydroxyquinoline (HL) solution (3.00% m/v, in ethanol) added dropwise from burette, with defined rate of addition. The mixture was leaved for defined time on the water-bath for re-crystallisation of the precipitate CdL2 at defined temperature, then filtered, washed with water, dried to a constant mass at 105˚C and weighed.

Figure 8. (a) The contraction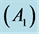 , reflection
, reflection 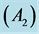 i expansion
i expansion  of the vertex
of the vertex  of the simplex ABC
of the simplex ABC  on the edge BC; and (b) Diminution of the simplex.
on the edge BC; and (b) Diminution of the simplex.
6.2. Decision Variables
Z1—re-crystallisation time [min] of the precipitated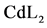 ;
;
Z2—mass [g] of tartaric acid added in the solution;
Z3—volume [ml] of NaOH added;
Z4—volume [ml] of 8-hydroxyquinoline added;
Z5—rate [ml/min] of 8-hydroxyquinoline addition;
Z6—temperature [˚C] of water bath where re-crystallization of  occurs;
occurs;
Z7—volume [ml] of the solution before precipitation.
For example, the value  [ml] refers to variable
[ml] refers to variable ; the related value
; the related value . For
. For  and
and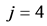 , from Table 1 we have
, from Table 1 we have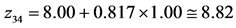 .
.
6.3. Results of Analyses within the Initial Simplex
The simplex optimisation procedure was realized in experiments performed in all points of the initial simplex (rows  in Table 1). In each point
in Table 1). In each point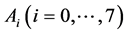 ,
,  measurements were done. The results mik[gCD/g] are presented in Table2
measurements were done. The results mik[gCD/g] are presented in Table2
On the basis of the data in Table 2, the  values were calculated (last column in Table 1).
values were calculated (last column in Table 1).
As results from detailed calculations done on the basis of results in Table 2, the inequality (23) has not been fulfilled within the initial simplex and then the evolution of the simplex was needed.
Referring to the Table 1, the worst  result within the initial simplex was obtained at the point
result within the initial simplex was obtained at the point . During the simplex evolution, this point was reflected in the centre
. During the simplex evolution, this point was reflected in the centre 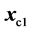 of the remaining points of the starting simplex. Referring to Table 1, we have, for example,
of the remaining points of the starting simplex. Referring to Table 1, we have, for example,



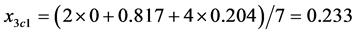

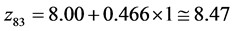
At the point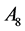 , the condition (24) has not been fulfilled as well, and further evolution of the simplex was required. The worst
, the condition (24) has not been fulfilled as well, and further evolution of the simplex was required. The worst  value within the new simplex was stated in the point
value within the new simplex was stated in the point . Further calculations referred to the new point
. Further calculations referred to the new point  are exemplified below:
are exemplified below:

 ,
,
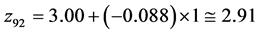 ;
;
Table 1. The values for zij assumed in points of the initial (columns 1-7, rows 0-7) and evolving (columns 1-7, rows 8-10) simplexes. For all points, the values  were obtained on the basis of
were obtained on the basis of 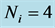 measurements.
measurements.
Table 2. Results of measurements done within the initial simplex.



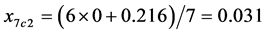
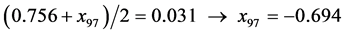 ,
,
 .
.
The coordinates of the new points: ,
,  and
and  for evolving simplexes, calculated with use of the coded variables
for evolving simplexes, calculated with use of the coded variables  specified.
specified.

The optimisation procedure has been terminated at the point , where
, where 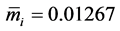 and variance
and variance  were found on the basis of 4 measurements and then the inequality (24)
were found on the basis of 4 measurements and then the inequality (24)
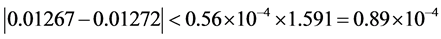
was fulfilled and

6.4. Optimal Prescription
On the basis of the optimization procedure, one can formulate the following prescription.
The samples, ca. 5 ml of the standardised CdSO4 solution, weighed on analytical balance (±0.1 mg), were taken for analysis. The solution was treated with 2.80 g of tartaric acid and then with 7.9 ml of 2.5 mol/l NaOH solution. After dilution with water up to ca 90 ml, the solution was treated with 7.7 ml of 3% (m/v) 8-hydroxyquinoline solution (added dropwise from burette, with the rate 1.4 ml/min. The mixture was leaved for ca. 90 min on the water-bath for re-crystallisation of the precipitate CdL2 at temperature 63˚C, then filtered, washed with water, dried to a constant mass at 105˚C and weighed.
7. Final Comments
In this paper, the simplex method has been presented in terms known from elementary algebra and geometry. On the basis of scalar product and length of vectors in normalized scale, the co-ordinates of simplex vertices in  space were determined. A criterion of optimization, where accuracy and precision of measurements were considered equivalently, has been suggested.
space were determined. A criterion of optimization, where accuracy and precision of measurements were considered equivalently, has been suggested.
The simplex method was considered as the most efficient among optimization procedures, applicable in simulating procedures realized in recursive computer programs used for simulation purposes and in optimization of analytical procedures. The simplex method requires only one additional experiment, regardless of the number of factors being varied. This drastically reduces the number of experiments required to reach the optimum.
References
- Anderson, V.L. and McLean, R.A. (1974) Design of Experiments: A Realistic Approach. Marcel Dekker, Inc., New York, 363.
- Nelder, J.A. and Mead, R. (1965) A Simplex Method for Function Minimization. Computer Journal, 7, 308-313. http://dx.doi.org/10.1093/comjnl/7.4.308
- Walters, F.H., Parker, L.R., Morgan, S.L. and Deming, S.N. (1991) Sequential Simplex Optimization. CRC Press, Boca Raton. http://www.chem.sc.edu/faculty/morgan/pubs/SequentialSimplexOptimization.pdf
- Spendley, W., Hext, G.R. and Himsworth, F.R. (1962) Sequential Application of Simplex Designs in Optimisation and Evolutionary Operation. Technometrics, 4, 441-461. http://dx.doi.org/10.1080/00401706.1962.10490033
- Fletcher, R. (1965) Function Minimization without Evaluating Derivatives—A Review. Computer Journal, 8, 33-41. http://folk.uib.no/ssu029/Pdf_file/Fletcher65.pdf
- Olsson, D.M. and Nelson, L.S. (1975) The Nelder-Mead Simplex Procedure for Function Minimization. Technometrics, 17, 45-51. http://dx.doi.org/10.1080/00401706.1975.10489269
- Fletcher, R. and Powell, M.J.D. (1963) A Rapidly Convergent Descent Method for Minimization. Computer Journal, 6, 163-168. http://dx.doi.org/10.1093/comjnl/6.2.163
- Fletcher, R. and Reeves, C.M. (1964) Function Minimization by Conjugate Gradients. Computer Journal, 7, 149-154.http://dx.doi.org/10.1093/comjnl/7.2.149
- Lagarias, J.C., Reeds, J.A., Wright, M.H. and Wright, P.E. (1998) Convergence Properties of the Nelder-Mead Simplex Algorithm in Low Dimensions. SIAM Journal of Optimization, 9, 112-147. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.120.6062&rep=rep1&type=pdf
- Box, G.E.P. and Hunter, J.S. (1957) Multi-Factor Experimental Designs for Exploring Response Surfaces. Annals of Mathematical Statistics, 28, 195-241. http://dx.doi.org/10.1214/aoms/1177707047
- Box, G.E.P. and Draper, N.R. (1969) Evolutionary Operation. John Wiley & Sons, Inc., New York.
- Massart, D.L., Vanderginste, B.G.M., Deming, S.N., Michotte, Y. and Kaufman, L. (1988) Chemometrics: A Textbook. Elsevier, Amsterdam.
- Massart, D.L., Vanderginste, B.G.M., Buydens, L.M.C., De Jong, S., Lewi, P.J. and Smeyers-Verbeke, J. (1997) Handbook of Chemometrics and Qualimetrics. In: Data Handling in Science and Technology, Vol. 22, Elsevier, Amsterdam.
- Box, G.E.P. (1957) Evolutionary Operation: A Method for Increasing Industrial Productivity. Journal of the Royal Statistical Society. Series C (Applied Statistics), 6, 81-101. http://en.wikipedia.org/wiki/EVOP
- Hahn, G.J. (1976) Process Improvement Using Evolutionary Operation. 204-206. http://rube.asq.org/statistics/2011/11/quality-tools/process-improvement-through-simplex-evop.pdf
- James, F. (2004) MINUIT Tutorial, Function Minimization, Geneva. Reprinted from the Proceedings of the 1972 CERN Computing and Data Processing School, Pertisau, 10-24 September 1972 (CERN 72-21). http://seal.web.cern.ch/seal/documents/minuit/mntutorial.pdf
- Liu, Q. (2001) Implementing Reusable Mathematical Procedures Using C++, C/C++. Users Journal.
- Walters, F.H., Parker Jr., L.R., Morgan, S.L. and Deming, S.N. (1991) Sequential Simplex Optimization. CRC Press, Boca Raton.
- Michalowski, T., Rokosz, A. and Wójcik, E. (1980) Optimization of the Conventional Method for Determination of Zinc as 8-Oxyquinolate in Alkaline Tartrate Medium. Chemia Analityczna, 25, 563-566.
- Palasota, J.A., Leonidou, I., Palasota, J.M., Chang, H.-L. and Deming, S.N. (1992) Sequential Simplex Optimization in a Constrained Simplex Mixture Space in Liquid Chromatography. Analytica Chimica Acta, 270, 101-106.http://dx.doi.org/10.1016/0003-2670(92)80096-P
- Deming, S.N. and Morgan, S.L. (1973) Simplex Optimization of Variables in Analytical Chemistry. Analytical Chemistry, 45, 278A-283A.
- Deming, S.N. and Morgan, S.L. (1983) Teaching the Fundamentals of Experimental Design. Analytica Chimica Acta, 150, 183-198. http://dx.doi.org/10.1016/S0003-2670(00)85470-7
- Umeda, T. and Ichikawa, A. (1971) A Modified Complex Method for Optimization. Industrial & Engineering Chemistry Process Design and Development, 10, 229-236.
NOTES

*Corresponding author.


