Received 30 March 2016; accepted 25 June 2016; published 28 June 2016

ABSTRACT

The purpose of this paper is to compare the efficiency of capitalistic and cooperative firms by focusing on the workers’ effort in production activity, when this effort is only known to workers, thus causing information asymmetries between workers and managers of both types of firms. Therefore, our model uses a principal-agents framework with workers’ hidden actions. The agency relations are not centered on the optimal design of incentive mechanisms but on the efficient (albeit incomplete) managerial monitoring of workers’ private effort. Moreover there is a trade- off between this monitoring activity and another managerial activity, i.e. the organization of production processes. We show that, taking into account the information asymmetries that characterize our model, the cooperative firm requires less monitoring than the capitalist firm to achieve the same efficient level of workers’ effort. This allows the manager of the former firm to devote more working time to organizational activity than the manager of the latter firm. In this respect, the governance of the cooperative firm dominates that of the capitalist firm. However, both types of firms need capital to operate and face different financial constraints in terms of the capital’s purchasing cost. These financial constraints affect the cooperative firm more severely than the capitalistic firm. Our conclusion is that these two types of firms have specific strengths and weaknesses, which make it difficult to reach general analytical results in terms of their relative efficiency. Additionally, the financial constraints characterizing the cooperative firm hinder maximization of its long-term growth rate; on the other hand, this kind of firm can better exploit the virtuous circle between increases in the employment level and increases in the growth rate.

Keywords:

Cooperative and Capitalistic Firms, Workers’ Effort, Governance, Agency Relations, Information Asymmetry, Social Consciousness

1. Introduction

This outcome represents a missed opportunity. Attention to agency costs and market failures put the focus back on Coase’s framework [38] and gave a solid analytical basis to Williamson's neo-institutionalist approach [39] - [41] . The consequent definition of the firm as a complex organization characterized by the internalization of a set of contractual nexus and their subordination to hierarchical relations (principle of authority) made the concepts of property rights and governance crucial. This offered a stronger theoretical justification for the coexistence of different kinds of firms in the market. A brief references to analytical steps that connect agency models to property rights and firms’ governance will be useful to clarify this point.

The presence of “incomplete contracts” and the designation of the firm as a “collection of physical activities” that represent the main components of the Hart-Moore [42] [43] models imply that the problem of attributing the residual rights of control is difficult to solve. Allocation of these rights in the form of property rights, which legitimize their holders to determine the utilization of non-human activities in all situations not regulated ex ante by contracts and to get residual income, is efficient if it rewards the type of agents that carry out the “indispensable” function in the firm.⁴ However, according to Hansmann’s analysis [32] , the attribution of property rights to “indispensable agents” minimizes agency costs only if these agents have the highest negotiation costs on the market. In any event, property rights introduce a non-contractual principle, which requires regulation with regard to the management of residual rights of control. In the definition of Rajan and Zingales [44] - [47] , a firm’s governance is precisely that complex system of (self)regulation that places constraints upon owners’ decisions and especially upon their ex post appropriation of residual income.⁵ Furthermore, compared to Hart and Moore [43] , Rajan and Zingales attach more importance to the neo-institutionalist concept of “specific investment”. Thus, the firm becomes a combination of activities and specialized agents, and appropriation of residual income depends on agents who made the most specific, and therefore riskiest, investments.

In this context, governance can be defined as the system of rules and constraints that shapes firm’s activities which are not guaranteed by external rules and contracts (i.e. contracts are incomplete). Such rules and constraints refer to decisions and ex ante negotiations as well as to monitoring and ex post distribution of the net income (cf. [46] ). Hence, agency relationships and governance offer powerful analytical tools to revisit, on a more modern theoretical basis, the comparison between cooperative and capitalist firms in terms of their respective degree of efficiency.

The purpose of this paper is to establish a comparison between these two kinds of firms by focusing on workers’ effort during the productive activity in a model where owners and/or managers suffer from information asymmetries. In the part dedicated to the cooperative firm (limited here to a cooperative of “production and work”; cf. infra), this comparison is interlaced with the assessment of costs and opportunities connected with the participation of workers in the firm’s capital. In our model, agency relations do not mainly pertain to the design of incentive mechanisms but rather the setting of an efficient form of monitoring, centered on management control (albeit incomplete) of workers’ effort during production. What emerges is that acquisition of ownership shares by each worker in the cooperative firm can reduce the efficient level of monitoring worker activity and increase the financing costs of productive capital. We conclude that, compared with the capitalist firm, the cooperative firm has efficiency advantages in terms of organizational activity but shows inefficiencies in capital acquisition.

To prove this conclusion, we first examine the objective functions of the two different firms (capitalist and cooperative) and specify the main assumptions characterizing the model (Section 2). It thus becomes possible to specify the problem of optimization in the capitalist firm with respect to the amount of managerial monitoring of worker activity as well as to the employment level (Section 3), and the analogous problem of optimization in the cooperative firm with respect to the amount of managerial monitoring and to the share of firm profits allocated to reserves (Section 4). The equilibrium conditions, which depend on the solution of these two problems of constrained maximization, provide a new approach to comparing the efficiency of these two types of firms.

This comparison leads to the result specified above: it does not allow us to establish whether the governance and organization of one of the two firms are more or less efficient with respect to those of the other (Section 5). As will be discussed in Section 6, to achieve a more precise overall result, we would need to extend our model to analyze the financial aspects of the two firms. However, the formalization of this extended model would require complex descriptive and analytical work exceeding the limits of this paper. It will then be sufficient to show that the results achieved, albeit still not a solution, are interesting and lead to a number of more immediate extensions of our model.

2. Framework

As suggested in the Introduction, the main differences between capitalist and cooperative firms can be stated by different forms of ownership and governance. Furthermore, since the 1990s, the economic literature has shown that different types of ownership and governance lead to different forms of corporate organization and control [32] [44] [48] - [50] . Therefore, our two objectives are to describe the specific forms through which capitalist and cooperative firms seek to attain optimal levels of organization and control with respect to their production processes and to define a relative measure of the efficiency achieved by these two firms with respect to such processes.

Besides reducing the two kinds of firms to a representative capitalist firm and a representative cooperative firm, our model makes the following assumptions:

1) no separation between firm ownership and firm management, so the capitalistic firm is an entrepreneurial firm and the cooperative firm is an organization of “production and work”;

2) the two types of firms, which operate in a market economy and are in competition, have the same technical production function and produce the same good;

3) the capitalist firm pursues the objective of maximizing its expected profits in the short term, while the cooperative firm aims to guarantee stable employment and an adequate income for its members through the entire period of their working life, maximizing long-term growth;

4) the owner of the capitalist firm holds the amount of capital required for the production process and can either utilize or sell it, while the cooperative firm has to purchase capital on the market;

5) workers’ compensation cannot be contingent on their effort since the latter is private information, and thus monetary wages are exogenously fixed at a set amount;

6) workers of both firms intend to maximize expected utility by supplying the lowest effort;

7) the entrepreneur of the capitalist firm and the manager of the cooperative firm are endowed with a set amount of effort usable either for organizing and managing the firm or monitoring worker activity;

8) worker effort is a stochastic increasing function of the managerial effort allocated to monitoring.

Assumption 1) implies that we neglect the possible problems of control which depend on different “agency relations”, i.e. we put aside the problem of separation between firm ownership and management as well as the possible conflicts between majority and minority shareholders.⁶ The owner of our capitalist firm, who holds the residual rights of control over production outcomes, also acts as the manager: she is responsible for the firm’s organization and the management of worker activity. The capitalist firm is thus assimilated to the entrepreneurial initiative. On the other hand, we bring the cooperative firm back to the “purest” form of mutuality―the organization of “production and work” in which all the workers are, pro quota, owners and collectively share the responsibility for their activities.⁷ To simplify the comparison with the capitalist firm, we assume that the manager of the cooperative firm does not belong to the set of owner-workers. However, this does not imply a separation between firm ownership and firm management since the owner-workers select the external manager on the basis of her acquired experience in the cooperative world and her adherence to cooperative principles. Hence, in the capitalist firm, there is an owner-manager (m = 1) and N workers and the only agency relation is between m and N; on the other hand, in the cooperative firm, there are N workers directly employed in the production process who are owners and who select an external pro tempore manager sharing cooperative objectives (m = 1).

Assumption 2) above builds a benchmark case based on the temporary exclusion of the problems and costs related to the monitoring of workers’ activity. Thus the capitalist and cooperative firms have the same production function. Each worker is endowed with a maximum capacity of effort (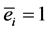; with), and he receives a wage w which, in the benchmark case, corresponds to the maximum and optimal effort level (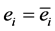). The stock of capital utilized in the production process by each firm is K.⁸ Therefore, in the benchmark case, the production function of the two firms is:

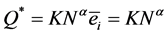(1)

where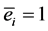, is the optimal quantity produced under the hypothesis above, and α (with 0 < α < 1) is the technical coefficient associated with labor such that.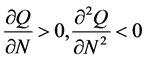

Since both firms operate in a market economy and are in competition, they have to comply with factors of efficiency and competitiveness. Assumption 3) above implies that the capitalist firm satisfies these two constraints by pursuing the objective of maximizing its expected profits in the short term―that is, the difference between current revenues and costs. The same assumption implies, on the other hand, that a cooperative firm aims to guarantee stable employment and an adequate income for its members throughout their working lives. Moreover, the cooperative firm aims for intergenerational fairness, often pursued by means of the “free entry” principle for new, young, and qualified members [2] . This complex set of objectives implies the realization of an optimal growth rate in the long term. For this reason, even at the risk of excessive simplification, we assume that the cooperative firm maximizes the share of its current profits set aside as an indivisible reserve, under the constraint of satisfying the mutuality principle by setting an amount of drawbacks commensurate with the different forms of contribution made by each single member.⁹

The output of each of the two firms is the quantity (Q) of a given good, which is the only one produced in the economic system. The supply price of this good is normalized to 1. Given assumption 4) above, the two firms face different constraints for starting their specific production process. At first glance, the capitalist firm only incurs the direct labor costs (w N) since the entrepreneur (owner) already holds the required capital (K). The cooperative firm, instead, has to purchase the amount of capital required for its production process on the market. As stated above, we assume here that each employee of the cooperative firm becomes an owner-member by buying a share (K/N of the capital K for a value equal to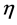; where: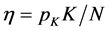, and p_K (from here on, just p) denotes the general price level of capital goods. The sellers of capital K are rentiers―ad hoc agents whose stock of goods and behavior are exogenous variables in our model. In principle, the seller of K could also be the entrepreneur of the capitalist firm who would thus forgo producing a portion of its output Q in order to play the role of rentier as well. For the sake of simplicity, we ignore this possibility here. However, its mere existence indicates that the capitalist firm (and not only the cooperative firm) has to bear, in addition to the labor cost, the cost of capital (pK; see also footnote 8). In this respect, the cooperative firm incurs a direct cost of purchasing K on the market, while the capitalist firm incurs the “opportunity-cost” of its entrepreneur. Both these costs, which are equal, have to be included in the production costs.

In the benchmark case analyzed here, i.e., when workers are independently controlled and thus supply their optimal effort without costly monitoring, the expected profit of each of the two firms is the same and equal to:

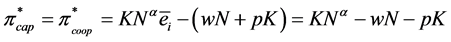(2)

At the end of the production process, the owner of the capitalist firm has the right to take possession of the whole amount of profit made by the firm; each owner-member of the cooperative firm, instead of the portion 1/N of the realized profit, obtains only 1/N of the difference between this profit and the stocked reserve.

In our model, the crucial problem is establishing whether (1) and (2) can be implemented when there is a standard problem of information asymmetry between owners and workers with respect to the effort supplied by the latter. In the literature, this kind of problem is solved by applying incentive schemes or imperfect monitoring schemes on worker activities (see, for instance, [23] [62] - [65] ). Assumption 5) states that the monetary wage is exogenously fixed (with w < 1), i.e., it is determined independently of the actual effort supplied by workers. This means that there is no room for incentive schemes based on variable remunerations, and owners and/or managers have to resort to an imperfect monitoring scheme.

The easiest way to introduce such a scheme is to maintain that, in both the firms in question, each worker obtains a utility 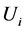(expressed in an additive form) directly from his activity. To comply with assumption 6), his utility is equal to the difference between the monetary wage and a monetary measure of his effort, since the latter is equivalent to a disutility whose unit value is fixed by the coefficient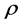.¹⁰ For the moment, we only take into account the component of utility directly related to the working activity with respect to the cooperative firm. It follows that each worker, whose objective function is the maximization of his own expected utility, aims to supply the lowest effort, given that the entrepreneur of the capitalist firm and the manager of the cooperative firm are unable to directly measure and control the above-mentioned effort because of information asymmetries, and given that the monetary wage is exogenously fixed as we assumed above. Equation (3) represents a simple formalization of what was previously stated with respect to the representative worker i (with i = 1, 2, , N):

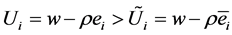(3)

for each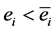; with

Equation (3) implies that, with asymmetric information and without a monitoring scheme, the limit would be: the lower the effort supplied with respect to the maximum level, the higher the utility of the worker and the lower his labor productivity. This prevents both firms from reaching the level of production and related profits determined by Equations (1) and (2) in the case of symmetric information. The managers of the two firms thus find it worthwhile to use their resources to reduce the information asymmetries and to control (albeit imperfectly) the effort supplied by workers. In this respect, assumption 7) above implies that the entrepreneur of the capitalist firm and the manager of the cooperative firm have a given amount of effort (normalized to 1) at their disposal, usable either to manage and organize the firm () or to monitor the workers’ activity ().¹¹

Since the entrepreneur is the sole owner of the capitalist firm, hence the only one who benefits from the entire amount of profits, she does not need any specific incentive to supply her maximum effort. That said, we should also assume that the entrepreneur is compensated with a remuneration s (with) for her managerial activity. Here, we assume that s = 0 without any loss of generality and in order to emphasize the other differences from the benchmark case. An analogous assumption applies to the effort of the manager of the cooperative firm. Even if the cooperative manager does not share ownership of the firm with the workers and hence does not hold any portion of firm’s capital, her full adherence to cooperative principles aligns her interests to the long-term objectives of the cooperative firm by construction. Thus, the problem lies in allocating the same and maximum amount of effort available for both managers between organization and monitoring.

The above considerations show that in (1), we established a relation between (=1) and Q^*, under the implicit assumption that the absence of information asymmetries implied. Instead, if we consider information asymmetries, would imply and hence and Q = 0. This means that, with information asymmetries, a share of the managerial effort must address the monitoring of workers (that is). As a consequence, ceteris paribus, Equation (1) would generate Q < Q^*, even if the monitoring effort of managers was fortuitously able to induce. Moreover, this monitoring effort is usually imperfect, such that and, a fortiori, Q < Q^*. In any event, under information asymmetries, assumption 8) above implies that the actual depends on. Therefore, Equation (1) becomes:

(4)

with;,

where

;

Equation (4) represents a sort of simplified version of the OR type production function (an “O-Ring function”) (see [66] ; [67] ), in which the effort of the single worker influences total output by a multiplicative rather than an additive operator. This means that total effort is a total product of the individual efforts instead of their summation. With respect to the original function OR, Equation (4) does not establish a total product between the efforts of the individual workers but rather between workers’ effort () and the share of the managerial effort () devoted to organization instead of monitoring. Hence, the optimal allocation of the managerial effort between and has to be determined.

To simplify the solution of this problem, assumption 8) also states that is a stochastic increasing function of the managerial effort allocated to monitoring. In particular, with () being the coefficient of the related linear function, we have:

(5)

with; where is the probability that a higher monitoring effort by manager m increases the level of effort of worker i, where indicates the minimum threshold (>0) of the latter effort with a probability () of evading monitoring (with).¹²

For the sake of simplicity, we assume that is constant and denote (with when). Equation (5) can therefore be rewritten as follows:

(5bis)

Equation (5bis) implies that the production function of the two firms, expressed by Equation (4), and the worker’s direct utility, expressed by Equation (3), can be respectively re-written as:

(6)

(7)

with

3. Model: The Capitalist Firm

Given the framework described in the previous section, it is possible to solve the maximization problems expressing the respective objective function of the two firms in question.

We start from the capitalist firm reduced to an entrepreneurial initiative. It is assumed that this firm pursues maximization of its short-term expected profit, i.e., maximization of the difference between current revenue and current monetary cost. The available capital (K) is given and fully depreciated in a single production process; therefore, the technical coefficient of production is:. The maximization problem is then reduced to a dual choice: the number of labor units to be employed (with N ≤ Ns¹³) and the amount of managerial effort () to be allocated to the firm’s organization rather than to monitoring worker activity. We therefore have to find the values of N and that maximize the expected profits of the capitalist firm, given that the wage (w) is exogenously determined and under the constraint that the workers’ expected utility must be greater or at least equal to the reserve utility (fixed, for simplicity, at 0¹⁴). In the case of the capitalist firm, the direct expected utility of each worker (see Equation (7)) coincides with his expected utility.¹⁵

The constrained maximization problem is:

(8)

and the Lagrangian becomes:

To find the optimal value of N and, we need to build up a system of equations that express the first order conditions.¹⁶ One of the functions to be maximized relates to the amount of optimal managerial effort dedicated to firm organization:

From this derivative, we obtain the value for the Lagrangian coefficient:

(9)

Another function to be maximized relates to the optimal choice concerning the amount of labor units (N):

.

This derivative leads to:

(10)

The third and last first order condition relates to the maximization of L with respect to the coefficient, that is:

From this derivative, we obtain the optimal value of the managerial effort to be allocated to firm organization rather than to monitoring workers:

(11)

with

It is possible to offer an economic interpretation of the equilibrium conditions deriving from the solution of the constrained maximization problem.

The first equilibrium Equation (10) determines the optimal level of employment in the capitalist firm as a function of labor productivity that, in turn, depends on the managerial effort devoted to firm organization and on monetary wage. Equation (10) can also be rewritten as:

(10bis)

Equation (10bis) underlines that the optimal amount of labor units to be employed in a capitalist firm is the amount that equalizes the marginal revenue to the marginal cost. The marginal revenue is equal to the marginal

productivity of labor (), given the normalization to 1 of the price of the produced good; the marginal cost is equal to the unit cost of labor (w).

The second equilibrium Equation (11) determines the optimal amount of managerial effort to be spent organizing the firm. This equation can also be written as:

(11bis)

Equation (11bis) shows that the optimal amount of managerial effort to be spent monitoring workers depends directly on the wage w and, inversely, on the following variables: the unit coefficient of the disutility associated to workers’ effort (), the possibility of workers eluding the impact of managerial monitoring (M), the reaction parameter of workers’ effort to managerial monitoring itself (), and the probability () that higher managerial monitoring effort could increase workers’ effort.

The economic interpretation of the direct relationship between w and () becomes obvious if we consider that, in our model, the monetary wage is exogenously determined. Every exogenous increase of w implies greater managerial effort spent monitoring worker activity since the latter are called upon to offer a higher actual effort in order to compensate for their wage increase. It is also evident that an increase in the reaction parameter or in the probability of a positive reaction by workers to managerial monitoring allows, ceteris paribus, acquisition of adequate worker effort with a lower managerial monitoring effort; for the owners, therefore, it becomes worthwhile to allocate more effort to the organization of the firm.

The economic interpretation of the inverse relations between and () and between M and () is less evident. At the first sight, these relations should be direct and not inverse. If there is an increase in workers’ disutility at any given effort or if there is an increase in the probability of workers eluding the impact of monitoring beyond the minimum effort threshold, these same workers will have an incentive to decrease their effort at least up to this threshold. As a consequence, greater managerial monitoring effort would be needed in order to avoid inadequate levels of worker effort. However, both these relationships could derive from failures in the organization of the production activities and/or in monitoring; every increase in () reduces the managerial effort for the organization of the firm (). It may thus be plausibly hypothesized that, if increases in () have a limited positive impact on due to the high value of and/or M, reducing the managerial effort devoted to monitoring whenever there are further increases in workers’ disutility or in the probability of workers eluding the impact of monitoring could be worthwhile. Hence, there are two opposite tendencies relating and M to (). Equation (11bis) shows that the second tendency dominates the first.

Equation (11) can be rewritten differently from (11bis) as:

(11ter)

Equation (11ter) suggests a much more intuitive economic interpretation than (11bis): it reproduces a typical condition of the theory of efficiency wages.¹⁷ The worker fixes his equilibrium effort in order to make it equal to the marginal increase in his utility (expressed by wage) and the marginal increase in the cost of the supplied effort (expressed by).

Beyond their variations and their specific economic interpretation, the two equilibrium Equations (10) and (11) show an important basic element. In the capitalist firm examined, the entrepreneur incurs a cost to determine the optimal level of employment and the optimal amount of monitoring workers’ activity: in order to achieve this result, the entrepreneur has to limit the effort allocated to the organization of the firm, which would increase its output. Hence, the activity of the capitalist firm is actually compelled to a trade-off: given that the entrepreneur has an available amount of effort normalized to 1, this amount has to be divided between monitoring workers and organizing the firm. If the entrepreneur had been able to check on the workers’ effort without a costly monitoring effort, these workers would have been forced to supply their maximum effort and the entrepreneur would have had the option to concentrate all effort on the firm’s organization. However, the presence of information asymmetries makes this hypothetical equilibrium (partly described by Equation (1), above) impossible to attain. Hence, the optimal equilibrium of N and, described by Equations (10) and (11), is always dominated by the equilibrium that could be achieved in the absence of information asymmetries.

Analysis of the activity of the cooperative firm, offered in the next section, aims to establish the cost of the trade-off described above and other possible costs incurred by this kind of firm. It will then be possible to compare the relative efficiency of the two types of firms with respect to the monitoring of worker effort and managerial organizational effort, as well as other possible costs.¹⁸

4. Model: The Cooperative Firm

To complete the analysis of the variables determining the workers’ choice of effort in the cooperative firm, three new factors have to be introduced.

The first factor was partly examined in Section 2. To become an owner-member of the cooperative firm, each worker has to buy a share of the capital on the market, i.e., , with a value equal to η (with, where p is the general price level of the capital goods). To simplify the following formalization, we consider such that. As we stated above, the total cost of the purchase of K (i.e., P) represents one of the production costs of the cooperative firm, so it enters the profits’ function (see Equations (2), (4) and (5) above):

On the other hand, having been borne by each worker of the firm, this cost can also represent a cost-opportu- nity for the workers themselves. In this respect, let us assume that there is an alternative allocation of η able to assure a riskless rate of return equal to r. The utility function of the single worker of the cooperative firm must then have a value at least equal to that of the reserve utility fixed by the alternative return r:

(12)

with 0 < r < 1.

The second factor is based on another aspect that we have highlighted several times: in the cooperative firm, workers are also owners, so they take possession of the distributed profits. Nevertheless, we have to remember that this kind of firm is characterized by the mutuality principle, and a fundamental component of this principle is based on the fact that the cooperative firm allocates most of its realized profits to a reserve fund and then the residue to drawbacks.¹⁹ Indeed, since the cooperative firm has the objective of fulfilling optimal long-term growth, it aims to maximize the share of its profits assigned to the reserve fund, under the constraint of assuring drawbacks compatible with the utility function of their worker-members. Let be the share of profits assigned to the reserve (where:); the remaining part of these profits, distributed between the worker-members of the cooperative firm in the form of drawbacks, is then equal to (). It follows that, for the cooperative firm, is to be added to as the choice variable.²⁰ On the other hand, the expected utility function of each worker-member is no longer reducible to his direct utility (see Equation (7), above) but has to be integrated with

his share of profits. In a first approximation, we would then have:

Not even the previous expression represents the complete form of the expected utility function of each worker of the cooperative firm. Indeed, this expression has to be integrated with another component of the mutuality principle that has been treated by Sen [71] in terms of “social consciousness”. “Social consciousness” has been disregarded in the representation of the cooperative firm, with rare exceptions (for instance: [72] ; [66] ), even though cooperative firms have an ownership structure and an organization that incentivize solidarity among workers.²¹ In our model, we can refer to the concept of “social consciousness” by assuming that the utility and, hence, the effort of the single worker also depends on the utility obtained by the other workers of the cooperative firm. This means that the utility of each member, beyond being a direct function of the wage received and of the distributed profits and drawbacks, as well as an inverse function of the effort supplied, is also positively influenced by the utility accomplished by the other workers of the cooperative firm thanks to their productive activity. indicates the coefficient evaluating that positive influence. Henceforth, will be termed the “social consciousness” coefficient. Furthermore, all the workers of the cooperative firm receive the same wage, exogenously fixed, and the same share of profits. The expected utility of the single worker of the cooperative firm then becomes:

(13)

with

Equation (13) can be rewritten as:

(14)

with.

Equation (14) is based on the fact that also depends on the employment level. From an economic point of view, this implies that the utility of worker-owners of the cooperative firm is also a direct function of the number of its employees. “Social consciousness” () and the other elements of the expected utility function being equal, each of the worker-owners of a cooperative obtains greater utility if his firm has a higher employment level. In this sense, the objective of the cooperative to optimize its own long-term growth can also be interpreted as the goal of maintaining high levels of employment in the long term (see also footnote 20).

Given these considerations, the problem of the constrained maximization problem of the cooperative firm is given by:

(15)

where: and

Therefore, the Lagrangian function is:

One of the first order conditions concerns the maximization of L with respect to the reserve to be stored:

It follows that the value of the Lagrangian coefficient is:

(16)

Offering formal confirmation of what is already realized by and Equation (14), Equation (16) proves that employment level remains a crucial factor in the operating of the cooperative firmfor our model as well. Indeed, if considered in the short term as an exogenous variable, Nrepresents a constraint on the indirect utility that each worker of the cooperative firmgains through the utility of other worker-members; furthermore, in the long term, N is approximated by one of the choice variables ().

Once the value of the Lagrangian coefficient is determined, we can specify a second condition of the first order by maximizing Lwith respect to the amount of management effort allocated to the organization of the cooperative firm ():

Given Equation (16), we determine the optimal level of:

(17)

The last first order condition concerns the derivative of L with respect to the Lagrangian coefficient:

It follows that the optimal value for the profits share to be stored as reserve is:

(18)

Let A denote the profit obtained by the cooperative firm for each employee, B the monetary wage received by each worker net of the effort supplied, C the opportunity cost borne by the worker to become member of the firm. Then:

It follows that Equation (18) can be rewritten as:

(18bis)

Equation (18bis) indicates that the cooperative firm finds it optimal to keep in reserve that share of the realized profits making the additional utility obtained by the owner-worker and his reserve utility equal.

The solution of the constrained maximization problem of the cooperative firm thus leads to the determination of the two equilibrium Equations (17) and (18). The latter equations show that, as in the case of the entrepreneur in the capitalist firm, the worker-owners of the cooperative firm also face a trade-off in order to determine the optimal share of profits to be stored as reserve and the optimal level of monitoring effort to be allocated to worker activity. If worker effort had been equal to 1 even without monitoring, the manager of the cooperative firm would have maximized her organizational effort. However, the presence of information asymmetries makes this hypothetical equilibrium (partly described by Equation (1), before) unattainable. Hence, the manager pro-tempore is obliged to limit the effort allocated to organizing the firm in order to monitor the workers. This limitation has a negative impact on the productivity and output of the cooperative firm. Moreover, if worker-owners gave up their rights to take possession of a positive share of the profits, the cooperative firm would employ all its resources for long-term growth and employment. However, the opportunity cost borne by worker-owners to buy their individual share of capital does not allow this kind of equilibrium. Therefore, as owners, workers limit the firm’s potential for long-term growth by taking possession of profit shares in the form of drawbacks.

As a result, the optimal equilibrium of and described by Equations (17) and (18) is lower than what would be achieved in the absence of information asymmetries with respect to the workers’ effort and in the absence of positive costs of becoming worker-members.

5. Comparing the Two Kinds of Firms

The analysis, developed in the two previous sections, shows that a comparison between the relative efficiency of the capitalist and cooperative firms in pursuing their specific objective functions does not lead to clear-cut results. In order to take a step forward, it may be useful to specify the influence exercised by some independent variables on the values of and in the case of the cooperative firm and to make a comparison, where possible, between the obtained results and the case of the capitalist firm.

Let us start from Equation (17), reproduced here with only a simple manipulation:²²

(17bis)

Equation (17 bis) shows that, similar to what happens in the capitalist firm, in the cooperative firm the optimal amount of monitoring effort spent by the temporary manager has an inverse relation with the following variables: the unitary coefficient of the monetary disutility related to the effort of workers (); the probability of the same workers eluding managerial monitoring (M); the relations between this probability and, respectively, the reaction parameter of worker effort to monitoring () and the probability () that a higher monitoring effort increases worker effort; the parameter (), which is a direct function of the “social consciousness” ().²³

These relations show that in the cooperative firm, as in the case of the capitalist firm, it is convenient to increase the organizational effort of the manager and to consequently decrease her monitoring effort whenever the positive impact of () on is low due to the high value assumed by and/or M.²⁴ Moreover, as in the case of the capitalist firm, the inverse relation between M and () is reinforced by the impact of and that, having a value between 0 and 1 and being placed as the denominator, increase the value of the relative ratio. However, Equation (17bis) shows that, in the cooperative firm, unlike what happens in the capitalist firm, the optimal amount of () does not depend on wages (w) but depends inversely on (the parameter of “social consciousness”). In order to compare the resulting monitoring cost incurred by management to give workers incentive to perform at an effort level maximizing the objective function of the two kinds of firms, it is then necessary to concentrate on this difference.

First of all,in the capitalist firm, ()is a direct function of w. By contrast,in the cooperative firmincreases in the degree of altruism, which is a component of the utility function of the individual worker-owners,and is now expressed by parameter, involve a reduction of (). It is easy to find an economic justification for this inverse relation between parameter and (): the increase in utility that each worker gets from the rise in the utility of his workfellows, and hence from the rise in output produced by the cooperative firm, albeit at the cost of greater individual labor effort, pushes every worker to increase his effort and to react more positively to the monitoring effort made by the manager. This means that, compared to the capitalist firm, the parameter of “social consciousness” in the cooperative firm reduces the rise in monitoring effort, imposed by a given increase of w. The result is that, ceteris paribus, in the cooperative firm, the optimal level of managerial monitoring is lower than in the capitalist one.

Another way to reach the same conclusion is by considering the parameterin a perspective slightly different fromthe one suggested by Sen [71] , butwhich is consistent with the assumption of interdependence of workersutilitiesin thecooperative firm. The ownership structure and the organization of this kind of firm make it convenient for the single workerto stimulate and control the efforts of hiscolleagues.It is a behavior long since studied in the economic literature and denominated “peer monitoring”.²⁵ The informal and decentered nature of this form of monitoring minimizes firm’s costs (cut down to 0 here), without affecting its efficiency. As a consequence, in the presence of efficient “peer monitoring” and other things being equal, a lower managerial monitoring effort is sufficient to obtain an optimal effort by workers. The typical ownership structure of the cooperative firm and the related utility function of its individual workers stimulate “peer monitoring”, further reducing the optimal monitoring effort to be spent by the manager. Each worker, holding an ownership share of the cooperative firm, benefits from making the relative production process as efficient as possible; he thus has an incentive to prevent his colleagues from shirking and to develop solidarity with them.

These results are reinforced by the fact that the cooperative firm does not need to take recourse in additional monitoring in the case of exogenous increases in employment. By contrast, Equation (17bis) shows an inverse relationship between N and the amount of monitoring; if the distinction between and is reintroduced (see footnote 23), Equation (14) displays a direct relation between N and. Both the equations thus show that, if the cooperative firm increases its employment, the amount of monitoring required by the manager in order to obtain optimal worker effort would decrease. The economic justification of this statement is a logical consequence of the previous considerations (see Section 4): if N increases, ceteris paribus, there will also be an increase in the utility of the single worker and/or stronger motivation to perform peer monitoring.

Here, it is important to underline that the opposite holds true for the capitalist firm. As indicated in Equations (10) and (11bis) (see Section 3), an increase in w (the optimal level of working effort) implies an increase in the employment level as well as the required amount of managerial monitoring. In this case, as well, the economic justification is evident: if N increases, the entrepreneur will have greater difficulty controlling each worker’ efforts and will have to increase her monitoring activity. However, the increase in N often comes with an increase in the organizational complexity of the capitalist firm. If this occurs, unlike the cooperative firm, the capitalist firm will pay for each increase in N with an increase in the cost of the trade-off, and the allocation of the managerial effort level between monitoring and organization becomes further sub-optimal.

What we just stated leads to an important but partial conclusion. If comparison between the capitalist firm and the cooperative firm were limited to the problem of worker oversight, we would be able to give a clear-cut answer to the question at the core of this paper: in a monitoring model of working activity, the cooperative firm pursues its objective function more efficiently than the capitalist firm. “Social consciousness”, i.e., solidarity among cooperative workers, explains this relative advantage. However, what has been disregarded until now is the other variable that the cooperative firm aims to maximize: the share of profits () stored in the indivisible reserve. To complete our analysis and the comparison with the capitalist firm, we thus have to examine the Equation (18bis), rewritten here as (18ter) by stressing the variable:

(18ter)

where:

A stands for the profits of the cooperative firm per worker, B the monetary wage collected by each worker net of the effort supplied, and C the opportunity cost borne by the worker to become member of the firm (with B < C).²⁶

The Equation (18ter) shows that the share of the stored profits is a direct function of the wage of each worker, net of the monetary value of the disutility deriving from the worker’s supplied effort, but an inverse function of the profits realized per worker and of the opportunity cost borne by workers to become members. Increases in the net wage raise the utility of each worker and erode the profits of the cooperative firm; the latter can, however, decrease the share () of profits attributed to worker-owners in the form of drawbacks. On the other hand, to raise the amount of profits realized per worker, the firm in question has to increase productivity and, hence, the effort supplied by all the workers. It is then understandable that the workers would want to be compensated for their greater disutility with an increase of (). It is finally expected that, if each worker could obtain higher financial returns outside the firm, he will choose to become a member only if () increases.

Equation (18ter) thus shows that, in the cooperative firm, there is always a trade-off between the degree of efficiency of the current production process and the maximization of long-term growth. Furthermore, this same equation emphasizes that, if potential worker-members have a better opportunity for risk-free investment in the financial market, it would be a further impediment to growth.²⁷ The various problems originating from such constraints do not only directly limit the rate of growth of the cooperative firm in the long term, but they also weaken the possible virtuous circle between increases in the employment level and growth rate. It could be maintained that similar constraints also affect the capitalist firm. However, this does not hold in our model. By assumption, the entrepreneur has enough capital to generate every production process available to the firm.

The comparison between the behavior of the capitalist firm and that of the cooperative firm in pursuing their specific objective functions is thus much less clear-cut than it appeared from Equation (17bis) alone. Indeed, our conclusion is that the relative efficiency of the two kinds of firm depends on whether monitoring costs prevail or not over financial costs.

6. Financial Aspects and Extensions of the Model

As previously stated, the advantages of the capitalist firm over the cooperative firm appear connected to the financial resources for the purchase of capital K. In the real world, these advantages could be less effective than what emerges from our model. For instance, the operational mode of the Italian economy, which is concentrated on small and microfirms (which come close to the entrepreneurial organization we examined), has often been stigmatized as “capitalism without capital”.²⁸ Financial constraints are set by the family wealth of entrepreneurs who are reluctant to share the control of their firms with non-relatives and to have recourse to the regulated capital market or even bond debt. Moreover, this kind of entrepreneur mistrusts external managers. It follows that small capitalist firm scan be drastically limited by financial constraints in developing successful activities and can be strongly dependent on the banking sector. On the other hand, some kinds of cooperative firms (most of all, consumer cooperatives) contract large amounts of stable low-cost debt (so stable as to come close to capital funding)―the members’ loans.²⁹ Moreover, a number of large cooperative firms have access to bank loan contracts that are not subject to more restrictive conditions than those offered to their capitalist competitors. That said, it remains true that capitalist firms normally use a wider spectrum of financial assets as regards cooperative firms.

Our previous model cannot take into account these aspects since the workings of financial markets is left in the background. To reach a more conclusive comparison between the organization and governance of capitalist and cooperative firms, it would thus be necessary to incorporate the financial funding of the two different firms as an endogenous variable. However, this requires a preliminary solution to a still open problem in the economic and legal analysis of cooperative firms: compatibility between the mutuality principle, which is a constitutive and essential characteristic of this kind of firm, and access to new financial assets.³⁰ Only by solving this problem would it be possible to combine the effort made by each worker of the cooperative firm to become one of the owners with the opportunities and management constraints to accessing different forms of funding. The consequent funding costs of the cooperative firm would then have to be compared with the corresponding cost of a capitalist firm willing to gain access to different financial instruments available on the market.

As far as we know, analysis of the financial aspects of the cooperative firm is no closer to supplying us with the answer we are looking for. Hence, rather than pursuing the goal of making the financial variables of cooperative and capitalist firms endogenous, we propose some more limited extensions of our model here.

First of all, even though it is the most analytically developed part, managerial monitoring can be further examined and extended. A first extension would be a more general formulation of firm monitoring and organizational costs as well as formalization of the related production functions. Then, with some modest algebraic manipulation, it would be possible to specify worker utility functions that are non-linear and take the workers’ degree of risk aversion into consideration. It would also be beneficial to diminish the contrast between short-term objectives in the capitalist firm and long-term objectives in the cooperative firm, without overlooking the distinction between the two firms and the related comparison between their degree of efficiency.

Secondly, the removal of some restrictive assumptions would permit a more elaborate representation of the organization of the cooperative firm. For example, specification of a more complex utility function of the representative worker would be useful to introduce not only risk aversion, but also a type of worker who does not share ownership of the cooperative firm. It would then be possible to distinguish between the utility functions of worker-owners and worker-non-owners in the cooperative firm, and then to compare both functions with that of workers in the capitalist firm. Our expectation is for there to be fewer differences between the utility function of worker-non-owners in the cooperative firm and that of workers in the capitalist firm than between the utility function of the former and that of worker-owners in the same cooperative firm. Nevertheless, the governance of the cooperative firm would still differ from that of the capitalist firm, and it would be possible to better debate the benefits and costs related to workers’ participation.

Thirdly, the organizational specification of the two different kinds of firms could be related to the different technology they adopt. At least in Italy, there is a low presence of cooperative firms at the technological frontier. This could be explained by the fact that the compared advantages of the cooperative firm are directly related to labor-intensive production processes, or it could stem from a different attitude toward risk on the part of capitalist entrepreneurs relative to worker-owners and cooperative managers.

Fourthly, it would be possible to make a more radical change to the analytical structure of our model by introducing the separation between ownership and management control in both types of firms. The capitalist firm would not be reduced to entrepreneurial activity, since it could take the form either of a firm with concentrated shares of ownership or of a public company (diffuse ownership). That said, in both these cases, the holder of property rights in the capitalist firm would be separate from the management. On the other hand, in the cooperative firm, the identification of the manager as a supporter of cooperative principles would no longer be valid: as often happens in the real world, management would be constituted by managers hired on the market competing with capitalist firms. Hence, management of the cooperative firm would be similar to that of the capitalist firm. The main analytical impact of such changes would be that, in each kind of firm, there would no longer be only one agency relationship but several (see Section 1). To our knowledge, there is no well-formulated model of partial equilibrium comparing the efficiency of capitalist and cooperative firms by means of different agency relationships within a unified framework.³¹

Finally, an even more profound innovation would be the endogenization of the monetary wage that was treated as an exogenous variable in our model. If monetary wage were to become a dependent variable, we would not only have a simple model of monitoring but a model that would have to also specify optimal incentive schemes to face moral hazard (and hidden action). The optimal combination of the incentive design and monitoring scheme would already be a thorny problem in a unified model. In our setting, we would also have to re- phrase the comparison between the two different firms in this complex new model.

7. Conclusions

Our principal-agents model has dealt with the problems of monitoring worker activity and capital constraints in a capitalist firm and cooperative firm.

From an analytical point of view, the part of the model dedicated to managerial monitoring of the working activity is the most developed. It proves that, in the presence of information asymmetries about the actual effort provided by each worker, the cooperative firm requires less monitoring to achieve the optimal level of worker effort. Also being owners of the firm and thus able to choose the person responsible for management functions among insiders, cooperative workers develop relations based on solidarity and forms of “peer monitoring” that reduce monitoring costs. Consequently, the manager of the cooperative firm can devote more effort to organizational activity, which increases the efficiency of the production process. Hence, in terms of working effort, governance in the cooperative firm is more efficient than in the capitalist firm.

However, an opposite result holds true for the purchasing cost of capital in the two kinds of firms. The analysis of this problem represents the less developed part of the model. Given that every worker of the cooperative firm can become a member only through buying a share of the capital on the market, it follows that his financial effort has to be remunerated with greater utility related to his working activity or drawbacks from profits made by the firm. Therefore, the financial constraints to the purchase of K reduce the production efficiency that the cooperative firm would achieve, if only managerial monitoring and the consequent organizing effort are considered. Moreover, the capital constraints represent an obstacle to achieving an optimal rate of long-term growth for the cooperative firm. It also dampens benefits related to the virtuous circle between increases in the level of employment and growth rate. Such inefficiencies and constraints are not present in the capitalist firm, even considering the opportunity cost to the entrepreneur from making the capital stock K available, which is in line with pursuing the objective of profit maximization.

The conclusion is that our model does not allow us to determine which of the two types of firms has the most efficient governance and organization. To achieve a more precise overall result, the model should be extended to analyze the financial aspects of the two firms and generalize the monitoring scheme. This extension and generalization would require complex descriptive and analytical work, which goes beyond the scope of this paper. Our intention is, however, tore-open the academic debate on fundamental topics such as ownership, control, and governance and to focus attention on important but less explored concepts such as the “social consciousness”, which seem, in certain economic organizations, to be a significant force driving investment and maximization decisions.

Cite this paper

Michele Alessandrini,Marcello Messori, (2016) Workers’ Effort: A Comparison between Capitalist and Cooperative Firms. Theoretical Economics Letters,06,601-620. doi: 10.4236/tel.2016.63066

References

NOTES

¹According to a Report issued by the International Co-operative Alliance “Global 300”, in 2013, the 300 largest cooperatives in the world produced a value added equal to 2360 billion dollars, which is the equivalent of the yearly GDP of the eighth largest economic system in the international market.

²See, for example [11] - [20] . For an extended in-depth review, see [21] .

³See, for instance [31] - [35] . In this respect, the most important contribution is offered by [36] and [37] .

⁴Hart and Moore ( [43] , p. 1133) define “indispensable” for a given activity the agent whose absence would render irrelevant the contribution of this same activity to the “marginal product of the investment” for the whole set of agents entering the contract.

⁵In the literature, we now have a large number of definitions of corporate governance. In descriptive terms, however, we can state that governance regulates a subset of relations between different groups of agents who hold specific interests in a given firm or company (stakeholders, obviously besides shareholders). Referring to fields usually regulated neither by primary norms nor by contractual agreements, governance is a form of (self)regulation that assesses the temporary power equilibria between different interest groups. Thus, the fields in which governance can apply vary from the relations between shareholders and management to the working of boards of directors and of firms’ control bodies, from self-regulation codes towards sellers and consumers to aspects concerning workers’ protection and involvement.

⁶One of the early analyses of the various types of agency relations characterizing the firm is offered by Jensen and Meckling [26] . An agency relation is defined by a contract, according to which the individual entitled to set the terms of the contract and to offer these contractual terms on the market (that is, the “principal”) delegates to other individuals (that is, the “agents”) the implementation of activities which are crucial for the fulfillment of her objective function. The usual problem is that the “principal” has an incomplete or asymmetric set of information, such that she is unable (a) to design and to offer a contract which includes all the possible future events, and (b) to exert a perfect and non-costly control on all the features and/or actions of the “agents”. Hence, in order to solve her maximization problem, the “principal” has to design suitable contractual terms to give the agents (who act in their own interests) the right incentives to self-select themselves or their possible actions according to her preferred ranking. Moreover, the “principal” can find it convenient to implement imperfect and costly monitoring of the activity actually performed by the “agents”. The costs, determined by the implementation of an ex ante and efficient incentive scheme, are termed agency costs; the costs, determined by the implementation of an imperfect ex post control, are termed monitoring costs. The relationships between shareholders and management typically lead to agency problems (see [48] , [51] , and [52] ); and the same applies to the public company or other forms of collective ownership, where the agency problems characterize the relationships between majority and minority shareholders [53] - [57] . Another typical agency relation outside the firm is that between lenders and borrowers. The only agency relation inside the firm, analyzed in this paper, is that between management and workers.

⁷There are three different categories of cooperatives, at least in Italy: workers’ cooperatives, users’ cooperatives, and services cooperatives. The cooperative firms of “production and work” (cooperative di produzione e lavoro) belong to the first category. We neglect the fact that, often in the real world, some workers are not members of the cooperative of “production and work”. From an analytical point of view, the workings of the different forms of cooperative firms in the three categories above can be reduced, directly or indirectly, with different degrees of approximation, to the workings of a cooperative of “production and work”. However, this general rule does not apply to consumers’ cooperatives or non-profit cooperatives. [58] , [59] , and [34] and [60] provide stimulating, but not conclusive, attempts to reduce the behavior of these two latter types of cooperatives to a common analytical framework. The topic of this paper―a comparison between the capitalist and cooperative firm―justifies the exclusion of non-profit activities; here, we extend this exclusion to consumers’ cooperatives.

⁸For the sake of simplicity, we assume that each firm completely consumes its available stock of capital in the current production process. Hence, we eliminate problems related to inventories and depreciation.

⁹Italian legislation regulating the activity of cooperative firms has changed dramatically in the past twenty years. Nevertheless, there is still an obligation today to transfer at least 30% of profits to a reserve that cannot be liquidated to members even in the future (“indivisible reserve”). This obligation is compliant with the mutuality principle, which is a crucial ingredient of governance of cooperative firms (cf. infra, footnote 19). Here, we assume that the cooperative firm aims to maximize the share of profits assigned to reserves (from here on, assimilated to the indivisible reserve), since this firm aims to keep growing in the long run. Therefore, as the legal rule of 30% does not represent a binding constraint from an economic point of view, it can be overlooked in the maximization problem of the cooperative firm (see below). Moreover, our model excludes all the agency problems between owners and managers by assumption, so we can neglect the possibility that managers pursue opportunistic behavior under the screen of objective functioning based on maximization of the reserve (cf. in this respect [61] ). On the other hand, current Italian legislation has placed limits, albeit not as severe as in the past (see the so-called “new company law”), to the share and form of profits that the cooperative firm can assign to owner-workers and to the different types of capital-members. Our model only refers to owner-workers. In this respect, the quantitative limits are determined by the Italian Civil Code itself: the distribution of profits over the law’s threshold must be decided by the firm’s assembly and must take the form of a drawback―that is, it has to be a function of the intensity of the mutualistic relationship, which each member holds towards the cooperative firm, and does not have to be proportional to the amount of capital given by each member. Here, we do not refer to the legislative details. However, the drawback being a component of the mutuality principle, our attempt is to meet the substance of the legal rule by assuming that the share of the profits assigned to the owner-workers is one of the binding constraints of the maximization problem of the cooperative firm.

¹⁰Let us recall that the price level of the single good produced is normalized to 1. We also emphasize that each of the employees of the cooperative firm has a more complex utility function, which also includes an indirect utility as specified in Section 4.

¹¹Let us state that, in accordance with the literature, we will describe the managerial effort to manage and organize the firm as organizational effort.

¹²In our model, the condition (0.5 < z_m,i) is an assumption required to obtain economically significant results. However, it is reasonable to apply a kind of Shapley rule to the expected impact of imperfect monitoring.

¹³Ns indicates the maximum amount of labor units available in our economic system at wage w. Strictly speaking, the condition N ≤ Ns would have to be incorporated as a constraint in the following maximization problem. In order to avoid a pointless complication, we assume that this constraint is always met as a strict inequality, that is, it is never binding.

¹⁴It must be noted that such a simplification cannot be extended to the case of the cooperative firm.

¹⁵This condition does not apply to the cooperative firm as well.

¹⁶The concavity of the production function, specified in Equations (1) and (4) (see above), makes it unnecessary to determine the second order conditions for the constrained solution of problem (8).

¹⁷This approach analyzes the positive but decreasing impact that wage increases have on the dynamics of labor productivity, and it shows that the minimization of the labor cost per unit of output is achieved at levels of w between a minimum and maximum level (cf. [68] ). Solow’s results have been refined and extended thanks to the examination of the possible links between efficiency wages and adverse selection mechanisms (cf. [69] ) or moral hazard mechanisms (cf. [70] ). Here, it is sufficient to note that, according to this approach, firms do not aim to minimize the level of w but find it convenient to increase wages up to the level coinciding with the minimum labor cost per unit of output.

¹⁸The comparison will be made in Section 5.

¹⁹The mutuality principle represents the crucial feature of cooperative governance. This principle is based on at least four elements: (i) the rule of “one head, one vote”, (ii) limits to the remuneration of the share of capital possibly contributed by non-worker-members, (iii) the choice and constraints to attributing a significant share of the yearly profits (net of the remuneration of the ordinary capital) to reserves, and (iv) the choice of transforming the share of the remaining net profits into drawbacks for members. Here, we assume that the total amount of capital was given by workers, so there is no problem of remuneration of the ordinary capital. We also assume that, beyond legal obligations, the mutuality principle latosensu can be reduced to element (iii) and to the consequent indivisibility of the cooperative firm’s reserves. The allocation of a significant portion of profits to reserve and the indivisibility of the latter introduce the distinction between maximization of profits acquired by the owners (maximization of the “subjective gain”), which cannot be dominant in the governance of the cooperative firm, and maximization of the firm’s growth (maximization of the “objective gain”), which is a pivotal point of this governance since it gives substance to the long-term guideline.

²⁰In comparison with the maximization problem of the capitalist firm, we thus find that replaces N. If we refer to the tradition initiated by Ward [10] , it may appear appalling that the cooperative firm does not include the employment level between its choice variables. The point is that, in our model, we list the short-term employment level among the exogenous variables. This level coincides with the number of worker-members; it would be analytically too complex to consider the number of worker-members as an endogenous variable. By contrast, the long-term employment level is indirectly included in the choice variables of the cooperative firm, since it is approximated by itself (cf. above, Section 2). Moreover, as will become clear, N indirectly enters the utility function of workers of the cooperative firm.

²¹In Sen’s model [71] , the agents are represented by “households”. Each household not only maximizes its utility (calculated by labor income and free time), but also includes the utility of other households in its preferences. This “social consciousness” (S), which is defined in the interval [0 ? 1], affects workers’ effort. In particular, if S is equal to 1, i.e., if each household considers the utility of other households as important as its own, worker effort will reach the optimal level independent of income distribution. On the contrary, if S becomes less than 1, i.e., if each household considers its utility more valuable than that of other households, workers’ effort will reach a suboptimal level. Sen’s analysis has been used in some papers devoted to the analysis of the workings of the Israeli Kibbutz [73] [74] .

²²Differently from Equation (17), in Equation (17bis), the dependent variable is represented by the managerial effort of monitoring instead of by the managerial effort of organizing the firm.

²³See also Equations (13) and (14). Moreover, it must be noted that and can be assimilated without any distortion in the analysis as long as the topic of employment is set aside.

²⁴In this respect, what has already been stated in relation to the capitalist firm remains valid (cf. above, Section 3).

²⁵This concept was used by [75] to analyze the workings of the credit market and by [76] to analyze those of the insurance market. Moreover, [77] referred peer monitoring to firm organization. For further analysis of the papers that applied the concept of peer monitoring to the cooperative firm, see [78] .

²⁶The assumption (B < C) can be justified by considering that, in our model, each worker-member of the cooperative firm would not find the remuneration of that firm acceptable if his income were mainly based on wages. (B < C) indicates that the difference between the reserve utility of each worker-member of the cooperative firm and his wage income is compensated by distributed profits.

²⁷In our model, the cooperative firm does not have direct access to financial markets and, hence, does not obtain any advantage from the improved efficiency of these markets. Our cooperative firm is financed solely by its members (see also Section 6).

²⁸The peculiar bank-oriented workings of the Italian financial market is reproduced through time by the limited amount of financing that the large majority of Italy’s small and very small firms and a significant part of its medium-sized firms obtain from financial sources other than self-financing and bank loans.

²⁹Members’ loans were initially classified as a form of risk capital and self-financing. Over time, changes in their regulation have, however, shown their true economic and legal nature: a form of debt, albeit incentivized and limited to the members. Here, it is impossible to address the problem in detail and point out the distortionary impact of members’ loans on the financial structure of cooperative firms. Being debt, members’ loans cannot solve the problems of undercapitalization, a typical feature of cooperative firms due to their problematic access to financial markets.

³⁰Recent legislation in Italy has allowed cooperative firms to access a number of financial resources. It is, however, worth pointing out that, on average, cooperative firms have made marginal use of such financial opportunities.

³¹Let us just note that, if the firm can be defined as a nexus of contracts dominated by the authority principle (see above), the roles of “principal” and “agents” become reversible and interchangeable. These roles would depend on the contract under examination. For instance, the holders of property rights play the role of “principals” in their relations with managers or workers, but they tend to play the role of “agents” in their relations with lenders. Moreover, a common label to indicate a given agency relation can hide very different problems in different firms.