Optics and Photonics Journal, 2012, 2, 326-331
http://dx.doi.org/10.4236/opj.2012.24040 Published Online December 2012 (http://www.SciRP.org/journal/opj)
The Efficiency of a p-n Solar Diode as a Function of the
Recombination Velocity within the Depletion Layer
Mohamed K. El-Adawi1, Najla S. Al-Shameri2
1Physics Department, Faculty of Education, Ain Shams University, Cairo, Egypt
2Physics Department, College of Science for Girls, Dammam University, Dammam, KSA
Received September 14, 2012; revised October 16, 2012; accepted October 30, 2012
ABSTRACT
The role of the carrier’s recombination velocity i
s
within the depletion Layer of junction solar cell and the ex-
ternal bias voltage across the junction in determining the current density “J” through the cell is revealed. The un-
steady carrier diffusion equation is solved under illumination conditions considering a source spectral function
-pn
a
V


G

.
The efficiency of the device as a function of i
s
, ,
a
V


G

is obtained. Computations considering a silicon solar cell
are given as an illustrative example.
Keywords: Efficiency; Diffusion Equation; Recombination Velocity
1. Introduction
The performance of a solar cell has aroused the interest
of many investigators [1-17]. The solar p-n cell is a
semiconductor photovoltaic cell. It is a passive trans-
ducer. It is fabricated such that one region is more highly
doped denoted by region. The density of the
charge carriers in the highly doped region may be of
three orders larger than the other region. This surface is
usually subjected to the incident illuminations (emitter
region). Due to large gradients, diffusion of charge carri-
ers take place, holes from
or np

P


region diffuse to the n-
region, while electrons diffuse from n-region to P

region. As a result a depletion layer is formed on both
sides of the contact metallurgical surface between both
sides. This layer is of small thickness and is
called as the space-charge region (SCR). This layer con-
tains the positive ions of the donner atoms on one side of
the contact surface and the negative ions of the acceptor
atoms on the other side, and thus an electric field is built
and one gets what is called the built-in-voltage

1μm



bi . It
is also called the contact potential or the barrier potential.
The direction of the electric field within the depletion
layer will be from the N-region to the P-region.
V
At equilibrium the net current (the sum of the diffusion
currents and the drift currents) through the depletion
layer must be zero. Now if the cell is subjected to an ex-
ternal reverse voltage bias, the established external field
will strengthen the internal one, and less current density
passes through the depletion layer and vice versa [18].
This bias voltage disturbs the thermal equilibrium state
of the device. When light strikes the highly doped sur-
face, the absorbed quanta excite the bound electrons and
electron-hole pairs are produced that move in all direc-
tions within the crystal [2]. The electron-hole generation
process is accompanied with recombination processes.
Now if the bias voltage is switched off, the built-
in-voltage will change towards its equilibrium value,
through a recombination process between the electrons
and the holes during the decay of the external voltage [3].
The equilibrium state will be restored within a time in-
terval

called as the relaxation time or it is defined as
the minority carrier life time .It is worth to note that the
electric potential across the depletion layer controls its
electric resistance [4]. Different factors affect the charge
transport properties within the cell, such as the electric
potential across the device, the recombination velocity
between the charge carriers. The most important factor is
the doping level [5,6]. This factor can be controlled
through the fabrication technology. These factors affect
the current density passing through the cell and thus
change its efficiency. Different trials are oriented to
study the performance of the solar cell through the study
of the recombination velocity between the charge carri-
ers.
With this respect one finds in principal two trends
namely:
C
opyright © 2012 SciRes. OPJ

M. K. EL-ADAWI, N. S. AL-SHAMERI 327
1) The first trend does accept the mechanism where
recombination occurs principally at one end surface of
the semiconductor device (usually it is the highly doped
one). In such a case the coordinate of such a surface is
taken as the origin x = 0, and a boundary condition ex-
pressing the charge continuity at this surface is given
[18]. Such a trend accepts also the study of this perform-
ance considering the collection efficiency of the base, the
emitter and the depletion layer [1,2,7-12]. It is shown
that the normalized surface recombination velocity de-
pends mainly on two parameters; these are the normal-
ized scanning range and the normalized depth of the gen-
eration volume (that is subjected to the incident light).
2) The second trend accepts the mechanism where an
effective interface recombination velocity i
s
that oc-
curs principally within the depletion layer at the metal-
lurgical interface [3,4,13,14]. Indeed, the effect of the
characteristics of the space charge region and the proc-
esses taking place within this layer has rarely been con-
sidered [3,9]. El-Adawi et al. [15] studied theoretically
the characteristics of the depletion layer. As a result, the
dependence of its thickness and capacity on the doping
ratio and the applied bias voltage is revealed. It is
worth to note that a restriction on the doping ratio
D
A
N
N
is also obtained [15]. A novel method [16] to estimate
experimentally the thickness of the depletion layer
is introduced.

6.7 μm

The main objective of the present article is to establish
a relation between the recombination velocity at the met-
allurgical interface within the depletion layer and the
current density which in turn affects the efficiency of the
solar cell. The unsteady carrier diffusion equation is
solved under illumination conditions.
2. Derivation of the Basic Equations
Consider a solar device (Figure 1), subjected to
incident solar flux
-pn



 and a bias voltage a. For the
unsteady state, the diffusion equation (after switching off
the bias voltage) is written for the minor charge carriers
in the form:
V
 




 
0
2
0
0
,
1
,
,,
n
nn
nxtn
nxtnDt
nxtnGx
DD



 


(1)
where

,nxt

3
m, the concentration of the minor charge carriers, .
0
i
a
n
nN , the concentration at equilibrium,


3
m.
i
n, is the intrinsic carrier,
P
+
n
Base
SCR
3
x
0
2
x
W
1
x
Figure 1. A model for the considered cell.
a
N, is the concentration of the acceptor atoms,

, the recombination life time (sec) , the diffusion
n
D
coefficient
2
sec
m





,Gx  , is the source function de-
fined as [1]



 
 
,1exp
exp
GxR x
x

 
 
  
 (2)
where,



 ,


21
secm the incident solar photon flux [17].

,


1
m absorption coefficient.
R, the reflection coefficient at the front surface.



 
1R   
Equation (1) is subjected to the following conditions:




  
0
0
00
,
0
,i
nx
ix
nxtn
at xDt
snxt n



 



0, 0
0
0 ,0,
exp ii
x
t
a
at xtnx t
qV
nkT






(ii) is a starting (initial) condition.


0
,0 iii
xw
at xWnx tn


where x = 0 is an arbitrary plane in the depletion layer
i
s
, the recombination velocity between the charge carri-
ers at the boundary x = 0.
a
W, is the width of the base region.
V is the applied bias voltage.
Let the solution of Equation (1) be in the form:
 
0
,,exp
t
nxtnvxt



 



(3)
Substitute Equation (3) into Equation (1) to get:




2
2
,,,
1exp
nn
vxtvxtG xt
Dt D x


 
 
 
(4)
The Fourier separation of variables method is used to
find the solution of the homogeneous part. This is ob-

M. K. EL-ADAWI, N. S. AL-SHAMERI 328
tained in the form:



2
,exp exp
cn

x
tA Dtx   (5)
where, ,
A
 are parameters.
While the particular solution can be obtained using the
inverse differential operator.
Equation (4) can be rewritten in the form:


2
exp
1exp
1
pn
xt
n
xt
D
DD
D











(6)
This gives the solution in the form:
 
2
,exp
,1
p
n
t
Gx
Vxt D






 (7)
Thus, the general solution can be written in the form:




2
2
,exp exp
,exp
1
n
n
x
tA Dtx
t
Gx
D

 







(8)
Substituting

,
x
t  into Equation (3) one gets the
required expression for n(x, t) in the form:


02
,
,expexp 1
n
Gx
nxtnAtxD


 

(9)
where,
21
n
D

 (10)
To find ,
A
 let us apply the boundary conditions.
This gives:




2
exp 1
ni
in n
Ds
At
sD D
 


 
 
 
(11)


2
01
ni i
n
nn
Ds
s
D
Df D
 
 

 





(12)
where,
00
exp 1
a
qV
fn kT



 





(13)
Finally, one gets the solution in the form:

02
,e ee
1
x
xx
n
nxtfD




 

 



(14)
where,



0
,,nxtnxtn 
The boundary condition (iii) makes it possible to get
the equation for in the form:
i
s
ln
1
i
n
sw
D





 (15)
where,
2
011 n
fD 







 (16)
Discussing the order of magnitude of different physi-
cal quantities included in expression (16) one can get the
following results:
01
f
 
φφ
i
n
s
D

φφ
This gives:
0e
i
n
Sw
D
f


 (17)
Equations (15) and (17) are very important expressions
since they establish a relation between the recombination
life time and the recombination velocity for the given
parameters.
3. The Efficiency
In order to estimate the efficiency, one has to compute
the charge current SC
J
according to the relation:

,
SC nn
nxt
JJqD
x

 
SC
J
is obtained in the form:


2
0
2
2
1
exp
1
,
1
n
nn n
n
n
fD
J
qD x
D
qD Gx
D
 

 







 


(18)
The efficiency

is expressed through the relation:
OC SC
sc in
F
FV J
JP   (19)
where,
FF the fill factor.
OC
V the open circuit voltage.
SC
J
the short circuit current.
in the input solar power absorbed at the front surface
of the solar device.
P
The open circuit voltage is given as [18].
OC
V
0
ln 1
sc
OC J
kT
VqJ






(20)
where,
23
1.38 10
J
k
K

 is Boltzmann constant.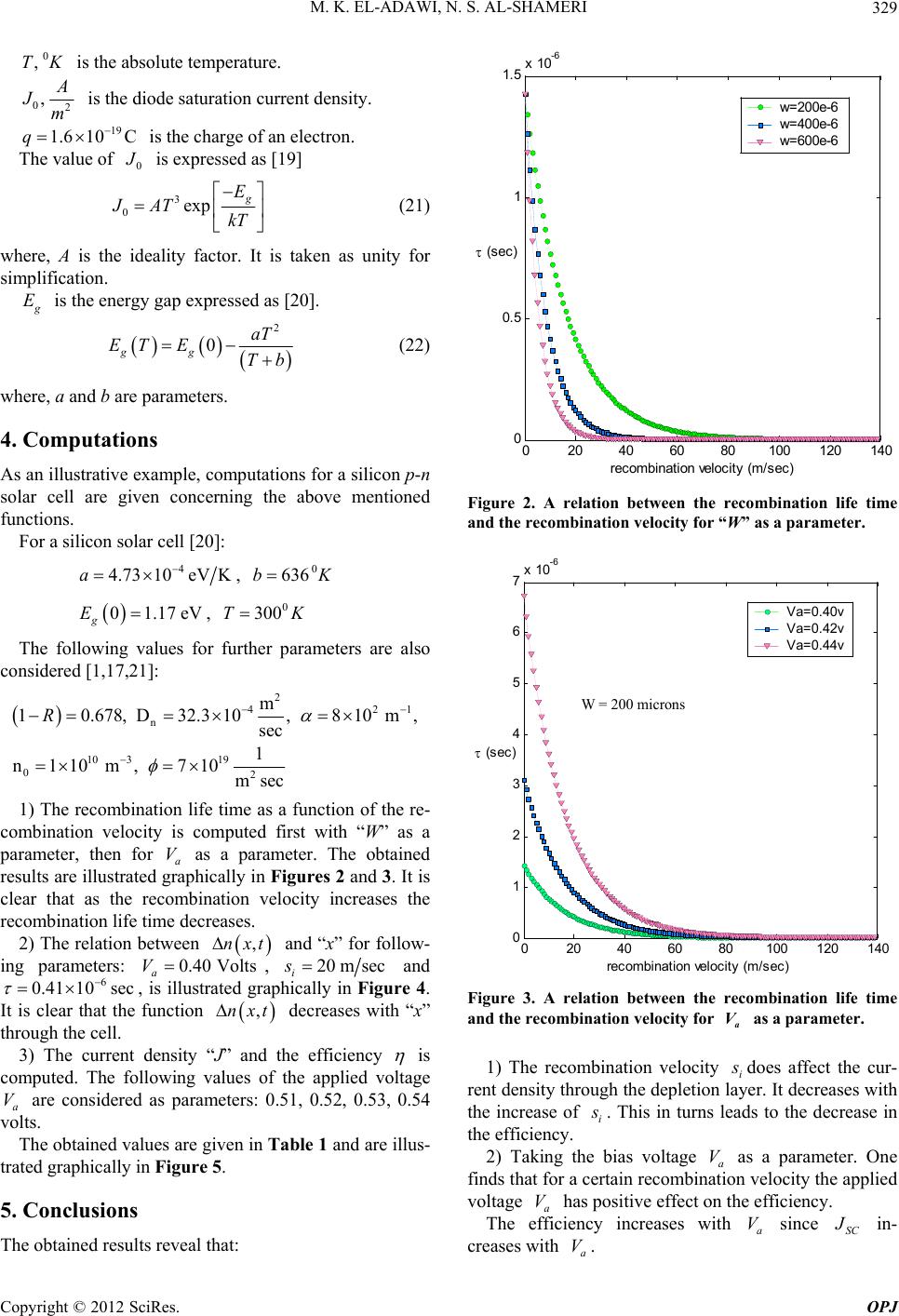

M. K. EL-ADAWI, N. S. AL-SHAMERI 329
0
,TK is the absolute temperature.
02
,
A
Jm is the diode saturation current density.
19
1.6 10Cq  is the charge of an electron.
The value of 0
J
is expressed as [19]
3
0exp g
E
JAT kT





(21)
where, A is the ideality factor. It is taken as unity for
simplification.
g
E is the energy gap expressed as [20].
 
2
0
gg
aT
ET ETb 
 (22)
where, a and b are parameters.
4. Computations
As an illustrative example, computations for a silicon p-n
solar cell are given concerning the above mentioned
functions.
For a silicon solar cell [20]:
4
4.7310eV Ka  ,
0
636bK

01.17eV
g
E,
0
300TK
The following values for further parameters are also
considered [1,17,21]:

2
421
n
10 319
02
m
10.678, D32.310, 810m,
sec
1
n110m, 710
msec
R




 
 
1) The recombination life time as a function of the re-
combination velocity is computed first with “W” as a
parameter, then for a V as a parameter. The obtained
results are illustrated graphically in Figures 2 and 3. It is
clear that as the recombination velocity increases the
recombination life time decreases.
2) The relation between


,nxt
Volts,
and “x” for follow-
ing parameters: a
V0.40 20msec
i
s
 ustrated graphically in Figure 4.
It is clear that the function
and
6
0.41 10sec

, is ill


,nxt es with “x”
through the cell.
decreas
3) The current density “J” and the efficiency

is
computed. The following values of the applied voltage
a are considered as parameters: 0.51, 0.52, 0.53, 0.54
volts.
V
The obtained values are given in Table 1 and are illus-
trated graphically in Figure 5.
5. Conclusions
The obtained results reveal that:
020 40 60 80100120140
0
0.5
1
1.5 x 10-6
recom b i n ation velocity (m /sec )

w=200e-6
w=400e-6
w=600e-6
(sec)
Figure 2. A relation between the recombination life time
and the recombination velocity for “W” as a parameter.
02040 6080100120140
0
1
2
3
4
5
6
7x 10-6
rec om bi nat i on veloc i t y (m/s ec)

V a=0.40v
V a=0.42v
V a=0.44v
(sec)
W = 200 microns
Figure 3. A relation between the recombination life time
and the recombination velocity for as a parameter.
a
V
1) The recombination velocity i
s
does affect the cur-
rent density through the depletion layer. It decreases with
the increase of i
s
. This in turns leads to the decrease in
the efficiency.
2) Taking the bias voltage a V as a parameter. One
finds that for a certain recombination velocity the applied
voltage has positive effect on the efficiency.
a
The efficiency increases with since
V
a
VSC
J
in-
creases with .
a
V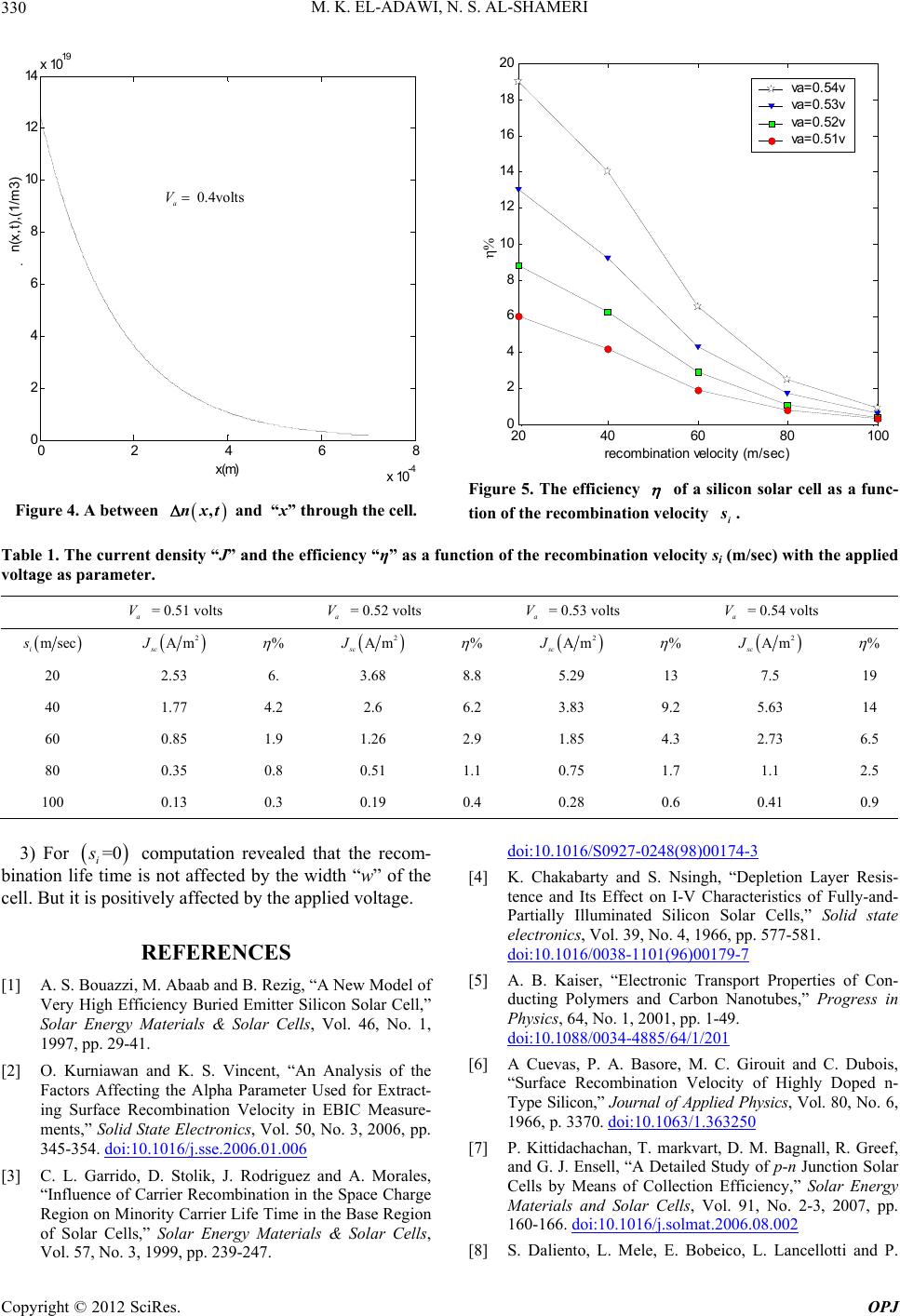

M. K. EL-ADAWI, N. S. AL-SHAMERI 330
20 4060 80100
0
2
4
6
8
10
12
14
16
18
20
recombination velocit y (m/s ec)

va=0.54v
va=0.53v
va=0.52v
va=0.51v
0246 8
x 1 0-4
0
2
4
6
8
10
12
14 x 1019
x(m)
n( x,t),(1/m3)
0.4volts
a
V
Figure 5. The efficiency

of a silicon solar cell as a func-
tion of the recombination velocity .
i
s
Figure 4. A between “x” through the cell.

,and nxt
Table 1. The current density “J” and the efficiency “η” as a function of the recombination velocity si (m/sec) with the applied
voltage as parameter.
a
V = 0.51 volts a V = 0.52 volts a V = 0.53 volts a V = 0.54 volts

msec
i
s

2
Am
sc
J %



2
Am
sc
J %



2
Am
sc
J %


2
Am
sc
J %

20 2.53 6. 3.68 8.8 5.29 13 7.5 19
40 1.77 4.2 2.6 6.2 3.83 9.2 5.63 14
60 0.85 1.9 1.26 2.9 1.85 4.3 2.73 6.5
80 0.35 0.8 0.51 1.1 0.75 1.7 1.1 2.5
100 0.13 0.3 0.19 0.4 0.28 0.6 0.41 0.9
3) For computation revealed that the recom-
bination life time is not affected by the width “w” of the
cell. But it is positively affected by the applied voltage.

=0
i
s

REFERENCES
[1] A. S. Bouazzi, M. Abaab and B. Rezig, “A New Model of
Very High Efficiency Buried Emitter Silicon Solar Cell,”
Solar Energy Materials & Solar Cells, Vol. 46, No. 1,
1997, pp. 29-41.
[2] O. Kurniawan and K. S. Vincent, “An Analysis of the
Factors Affecting the Alpha Parameter Used for Extract-
ing Surface Recombination Velocity in EBIC Measure-
ments,” Solid State Electronics, Vol. 50, No. 3, 2006, pp.
345-354. doi:10.1016/j.sse.2006.01.006
[3] C. L. Garrido, D. Stolik, J. Rodriguez and A. Morales,
“Influence of Carrier Recombination in the Space Charge
Region on Minority Carrier Life Time in the Base Region
of Solar Cells,” Solar Energy Materials & Solar Cells,
Vol. 57, No. 3, 1999, pp. 239-247.
doi:10.1016/S0927-0248(98)00174-3
[4] K. Chakabarty and S. Nsingh, “Depletion Layer Resis-
tence and Its Effect on I-V Characteristics of Fully-and-
Partially Illuminated Silicon Solar Cells,” Solid state
electronics, Vol. 39, No. 4, 1966, pp. 577-581.
doi:10.1016/0038-1101(96)00179-7
[5] A. B. Kaiser, “Electronic Transport Properties of Con-
ducting Polymers and Carbon Nanotubes,” Progress in
Physics, 64, No. 1, 2001, pp. 1-49.
doi:10.1088/0034-4885/64/1/201
[6] A Cuevas, P. A. Basore, M. C. Girouit and C. Dubois,
“Surface Recombination Velocity of Highly Doped n-
Type Silicon,” Journal of Applied Physics, Vol. 80, No. 6,
1966, p. 3370. doi:10.1063/1.363250
[7] P. Kittidachachan, T. markvart, D. M. Bagnall, R. Greef,
and G. J. Ensell, “A Detailed Study of p-n Junction Solar
Cells by Means of Collection Efficiency,” Solar Energy
Materials and Solar Cells, Vol. 91, No. 2-3, 2007, pp.
160-166. doi:10.1016/j.solmat.2006.08.002
[8] S. Daliento, L. Mele, E. Bobeico, L. Lancellotti and P.

M. K. EL-ADAWI, N. S. AL-SHAMERI 331
Morrillo, “Analytical Modeling and Minority Current
Measurements for the Determination of the Emitter Sur-
face Recombination Velocity in Silicon Solar Cells,” So-
lar Energy Materials & Solar Cells, Vol. 91, No. 8, 2007,
pp. 707-713. doi:10.1016/j.solmat.2006.12.007
[9] F. A. Lindholm, L. Juinj and A. N. Schel, “Determination
of Life Time And Surface Recombination Velocity of p
n-Junction Solar Cells And Diodes by Observing Tran-
sients,” IEEE Transactions on Electron Devices, Vol. 34,
No. 2, 1987, pp. 277-285.
[10] S. N. Singh and P. K. Singh, “Modeling of Minority-
Carrier Surface Recombination Velocity at Low-High
Junction of an p-n Silicon Diode,” IEEE Transaction on
Electron Devi ces, Vol. 38, No. 2, 1991, pp. 337-343.
doi:10.1109/16.69915
[11] S. S. de, A. K. Ghosh, M. Bera, A. Hajra and J. C. Halder,
“Influence of Built-in-Potential on the Effective Surface
Recombination Velocity for Heavily Doped High-Low
Junction,” Physics B: Physics of Condensed Matter, Vol.
228, No. 3-4, 1966 , pp. 363-368.
[12] S. Kumar, P. K. Singh, G. S. Chilana and S. R. Dhariwal,
“Generation and Recombination Life Time Measurement
in Silicon Wafers Using Impedance Spectroscopy,” Semi-
conductor Science and Technology, Vol. 24, No. 9, 2009,
pp. 1-8, Article ID: 095001.
[13] J. F. Gibbons, “Semiconductor Electronics,” McGraw-
Hill, New York, 1966, Chapter 6.
[14] M. Saad and A. Kassis, “Effect of Interface Recombina-
tion on Solar Cell Parameters,” Solar Energy Materials &
Solar Cells, Vol. 79, No. 4, 2003, pp. 507-517.
doi:10.1016/S0927-0248(03)00101-6
[15] M. K. El-Adawi and N. S. Al-Shameri, “On the Deple-
tion Layer,” Material Science Research India, Vol. 6, No.
1, 2009, pp. 73-78.
[16] H. Awaki, K. Tachibana, Y. Tamai, K. Yamamoto, S.
Kitamoto and M. Tsujimoto, “A Novel Method to Esti-
mate the Thickness of the Depletion Layer of an X-Ray
CCD,” Nuclear Instruments & Methods in Physics Re-
search (Sect ion A), Vol. 495, 2002, pp. 232-239.
[17] M. K. El-Adawi and N. S. Al-Shameri, “The Efficiency
of the Solar Converter as a Function of the Doping De-
grees and the Incident Solar Spectral Photon Flux,” Ca-
nadian Journal on Scientific and Industrial Research, Vol.
3, No. 3, 2012, pp. 112-122.
[18] S. M. Sze, “Physics of Semiconductor Devices,” Wiley,
New York, 1981.
[19] M. A. Green, “Solar Cells,” Prentice-Hall, Englewood
Cliffs, 1982.
[20] R. F. Pierret, “Semiconductor Devices Fundamentals,”
Addison-Wesley Publishing Company, Boston, 1996.
[21] A. Bhattacharyya and B. G. Streetman, “Dynamics of
Pulsed CO2 Laser Annealing of Silicon,” Journal of Ap-
plied Physics, Vol. 14, No. 5, 1981, pp. 67-72.