Journal of Service Science and Management, 2012, 5, 355-364
http://dx.doi.org/10.4236/jssm.2012.54042 Published Online December 2012 (http://www.SciRP.org/journal/jssm) 355
Bank Branch Grouping Strategy, an Unusual DEA
Application
Barak Edelstein, Joseph C. Paradi, Adria Wu, Petty Yom
Centre for Management of Technology and Entrepreneurship, Faculty of Applied Science and Engineering, University of Toronto,
Toronto, Canada.
Received October 16th, 2012; revised November 19th, 2012; accepted November 26th, 2012
ABSTRACT
This study uses Data Envelopment Analysis (DEA) to develop a grouping strategy for the bank branches of a large Ca-
nadian Bank. In order to benchmark their branches’ performance, the Bank first clusters the branches based on commu-
nity type and population size—a not fully satisfactory approach. Hence, DEA was used to develop a grouping approach
using an input oriented BCC production model to capture and analyze the aggregated effects of many complex proc-
esses. The model examines the relationship between staff and transaction activities. The peer references produced by
the DEA model illustrate that the Bank’s current clustering methodology fails to compare some branches that are simi-
lar from an operational perspective; a flaw in the Bank’s current grouping approach. The new grouping strategy offers a
fair and equitable set of benchmarking peers for every inefficient branch.
Keywords: Data Envelopment Analysis; DEA; Benchmarking; Grouping; Clustering; Data Sorting;
Process Improvement; Productivity; Bank Branch
1. Introduction
In this paper Data Envelopment Analysis (DEA) is used
to sort data rather than assess the un its’ efficiency or pro-
ductivity. The work was inspired by a problem one of the
major Canadian banks had when they attempt to bench-
mark their branches’ performance. While we had done
several studies in bank branch efficiency [1-5], this ef-
fort was to help them see that grouping their branches for
any comparative reason should be done in a different
manner than simply using location or size as the crite-
rion.
1.1. The Canadian Banking Industry
The Canadian banking industry is becoming increasingly
competitive with a total of 66 banks operating in Canada,
including 21 domestic banks and 45 foreign banks. To-
gether these 66 banks operate over 5900 branches in
Canada, employ over 249,000 people, and manage al-
most $1.8 trillion in assets [6]. In addition, the largest
five banks also carry on extensive businesses via banks
owned outside of Canada and have significant presence
in other financial services areas such as insurance, secu-
rities brokerage and trust activities.
The banks in Canada conduct much of their business
and compete with each other through their branch net-
works. The branch network is the bank’s main vehicle
for contact and the management of relationships with
customers. Furthermore, the banks are placing renewed
emphasis on their branch channel and are aggressively
expanding them. This is a turnaround from a decade ago
when they were busy closing branches and consolidating
their branch network. It is therefore important for banks
to be able to evaluate and improve the performance of
their branch networks.
Banks use grouping strategies in order to cluster bran-
ches into comparable peer groups with the purpose of
comparing the performance of branches within each peer
group, often using simple ratios. Banks typically use geo-
graphic and demographic factors to sort bank branches
into peer groups, but these factors often ignore opera-
tional similarities and differences between them as they
concentrate on regional or demographic factors. Such
clustering approaches can create peer groups that are
composed of operationally dissimilar branches which
cause branch managers to push back when they are con-
fronted with performance appraisals that show them in a
poor light. It is crucial to not only make such compari-
sons fair and equitable, but it must be seen to be such
when viewed by those being measured. Therefore, it
would be very advantageous to group or cluster opera-
tionally similar branches into peer groups which can be

Bank Branch Grouping Strategy, an Unusual DEA Application
356
seen to be appropriate, thus making the within group per-
formance evaluations and the resulting performance tar-
gets fair and potentially easier to accept, and more im-
portantly to be acted upon.
1.2. Data Envelopment Analysis
Data Envelopment Analysis (DEA) is a non-parametric
linear programming (LP) methodology that defines a
convex piecewise linear efficient frontier composed of
the best performing decision making units (DMUs), and
calculates relative efficiency scores for the inefficient
DMUs by measuring their relative distance to the effi-
cient frontier. For each inefficient unit DEA provides a
set of improvement targets and efficient benchmarks al-
lowing management to identify best practices in at-
tempting to improve the performance of the inefficient
units, and in setting improvement goals [7]. DEA can
handle multiple inputs and outputs simultaneously and
does not require specification of a production function
for the model’s variables [7]. In complex service indus-
tries such as the banking industry many of the input-
output relationships are unknown, especially when ex-
amining multiple inputs and outputs simultaneously.
DEA in its constant returns to scale (CRS) form, known
as the CCR model, was introduced in 1978 by Charnes,
Cooper, and Rhodes [8]. The BCC model introduced by
Banker, Charnes, and Cooper in 1984 provided the vari-
ables returns to scale (VRS) DEA formulation [9]. In
1985 Sherman and Gold used DEA to study the produc-
tion efficiency of bank branches [10]. Since then many
studies have used DEA to measure the efficiency of bank
branches [2]. These studies can be classified into several
categories including production, profitability, and inter-
mediation. The production approach, which is used in
this study, analyzes the bank’s branches from an opera-
tional perspective where a branch uses inputs such as
labor to produce output transactions such as deposits and
loans.
DEA has several advantages over the performance ra-
tios that are often used by the banks to evaluate branch
performance. While ratios are simple to use and rela-
tively easy to understand, their level of simplicity can be
problematic in trying to see the big picture which incur-
porates many different aspects. Ratios examine the pro-
portional relationship between two specific variables, but
they fail to incorporate the multiple variables that must
be examined together to fully understand the situation.
No single ratio should be used to come to conclusions
about the performance of a branch, but rather in examin-
ing the overall state of a branch a variety of ratios must
be considered together. Simultaneously considering or
aggregating the results of different ratios can be mis-
leading by potentially masking underperformance and
relationships that exists in the data. Index numbers are
often used to aggregate several weighted variables or
ratios thus considering several factors at the same time.
However, problems can arise from the selection of the
weights used in calculating index numbers. Performing a
multi-dimensional analysis such as DEA that considers
all the pertinent variables simultaneously and does not
require specifying a production function for the model’s
variables can provide a single aggregated performance
indicator that better represents the overall state of the
branches’ performance.
As DEA is a well known operational research method-
ology, since this paper assu mes only introducto ry famili-
arity with DEA, we will not repeat the theoretical and
mathematical derivation of the approach. If the reader
needs to learn more about the basics of DEA, we refer
you to the excellent book on DEA by Cooper, Seiford
and Tone [7].
The rest of the paper is structured as follows. It begins
with an outline of our motivations for the study and the
issues that arose from the present method used by the
Bank. In Section 3 we show the methodology used and
the rationale for what models were employed. Then, in
Section 4 we report on the results achieved and show
how the work can be utilized in the real world of this
Bank. The paper concludes with a summary of the find-
ings and this is presented in Section 5.
2. Motivation and Goals
The bank in this study is one of Canada’s largest five
banks. It operates over 1000 branches in Canada and
offers a full range of banking services. In order to pro-
duce meaningful evaluations of their branches’ perform-
ance, the Bank currently groups branches into seven clu-
sters (categories) based on the community type and po-
pulation size in the area in which they operate, as shown
in Table 1 below [11].
Table 1. Description of the Bank’s current peer groups.
GroupDescription of location
A Downtown area of a city with a population > 500K
B Adjacent to the downtown area of a city with a popula-
tion > 500K
C Adjacent to the urban area of a city with a population >
500K, including commuter are as
D City with a population between 250K and 500K
E Community with a population between 25K and 250K
F Community with a population < 25K
G Community with a population < 10K and >2 hrs drive
from an urban center

Bank Branch Grouping Strategy, an Unusual DEA Application 357
The Bank utilizes its peer grouping in develop ing stra-
tegic targets and evaluating performance through peer
benchmarking, mostly through the use of performance
ratios. Under the Bank’s current peer grouping method-
ology, group members can hav e significan t differences in
their operations and structure yet would be compared to
each other due to general similarities in the locations out
of which they operate. However, branches that are opera-
tionally similar are often grouped into different clusters
and are thus not compared to each other. The Bank’s
current grouping strategy uses somewhat arbitrary popu-
lation cutoff levels (10K, 25K, 250K, and 500K) to dis-
tinguish between peer groups. By clustering branches in
such a way, the Bank ignores other factors such as
branch size and the characteristics of the branches’ cus-
tomer base which affect the quantity and type o f tran sact-
tions that the branches produce. The geographical and
population size dependence of the Bank’s grouping stra-
tegy are often no t reflective of operational similarity and
the inclusion of branches in one peer group or another is
again done somewhat arbitrarily.
Consider for example the City of Hamilton and the
former Town of Dundas (both located in southern On-
tario, Canada). Hamilton and Dundas are in close prox-
imity to each other, and were amalgamated in 2001. In
1996 Hamilton had a population of 322,352 [12] and
bank branches in Hamilton would have therefore be-
longed to Group D, while Dundas had a population of
23,125 [12] and its branches would have therefore be-
longed to Group F. Being in very close proximity to each
other, the communities of Hamilton and Dundas are ar-
guably similar and their populations and businesses are
intertwined. Therefore, to group branches in Hamilton
and Dundas into such different peer groups is problem-
atic. Rather than being compared to branches in Hamil-
ton and other such similar urban communities, branches
in Dundas would have been compared to other branches
in Group F some of which are located in small remote
communities.
After the 2001 amalgamatio n of Hamilton and Dundas
along with other small towns in the vicinity, the popul-
ation of the newly amalgamated City of Hamilton grew
to 490,268 as shown in the 2001 Canadian Census,
mainly due to the amalgamation as the real population
growth since 1996 was only 4.8% [13]. The Government
of Ontario’s decision to amalgamate Hamilton and Dun-
das meant that in 2001 branches in Dundas, which were
previously in Group F, would have been included in
Group D and compared with other urban branches in that
group. In addition, the 2006 Census showed that while
the population of the amalgamated City of Hamilton
grew by less than 3% between 2001 and 2006, it reached
a level of 504,559 in 2006 [14] and therefore surpassed
the arbitrary level of 500K set by the Bank. Conse-
quently, in 2006, the branches of both Hamilton and
Dundas would have been clustered into Groups A, B, or
C and would have been compared to other branches in
those groups instead of being compared to branches in
group D to w hich Hamilton an d Dundas belonged b efore
2006. Furthermore, any smaller communities which would
have been defined by the Bank as being adjacent to
Hamilton, or commuter areas of Hamilton, would have
also been included in Group C after the amalgamated
City of Hamilton surpassed the arbitrary 500K popula-
tion threshold. Finally, it could be argued that branches
in Hamilton which is less than 70 km away from Can-
ada’s largest city, Toronto, along with all the bran ches in
between the two cities should have been grouped to-
gether with branches in Toronto. It clearly makes more
sense and results in a more credible approach as most
people would agree that due to strong economic and
demographic similarities and dependencies of th ese com-
munities such grouping would be more acceptable. We
will show that the Bank’s current grouping strategy is
quite arbitrary at times as it fails to group operationally
similar branches together, sometimes leading to inappro-
priate comparisons between branches and failing to
compare branches that operate in a similar manner.
There were two main drivers in this study. First, the
Bank needs a more comprehensive and defendable branch
grouping methodology before they do any credible bench-
marking. Second, a better data sorting tool such as DEA
could make the branch grouping process fairer and more
equitable.
The work encompassed an approach to sorting bran-
ches and then comparing the results to the approach the
Bank uses. This was to convince management and branch
staff that the DEA method is better from a number of
points of view. Our work resulted in a defendable ap-
proach to a new grouping technique for the Bank for its
inefficient branches by utilizing DEA efficient peers.
3. Methodology
Before we delve into the methodology employed here, it
is instructive to recall the one paper from the literature by
Thanassoulis [15] where he examined the efficiency of
police forces in England and Wales. Given that police
forces operate in different demographical areas, com-
parison to peers which operate under better circum-
stances is unfair to those police units which have to deal
with more perpetrators without fixed addresses and in
communities where the people do not readily cooperate
with police. To address this problem, Thanassoulis [15]
had introduced a variable that reflected the social and
economic deprivation of the district covered by the spe-
cific police unit. This variable was an index that had both
positive and negative values, but the base index was ar-
bitrary and there was little confiden ce in it as a represen-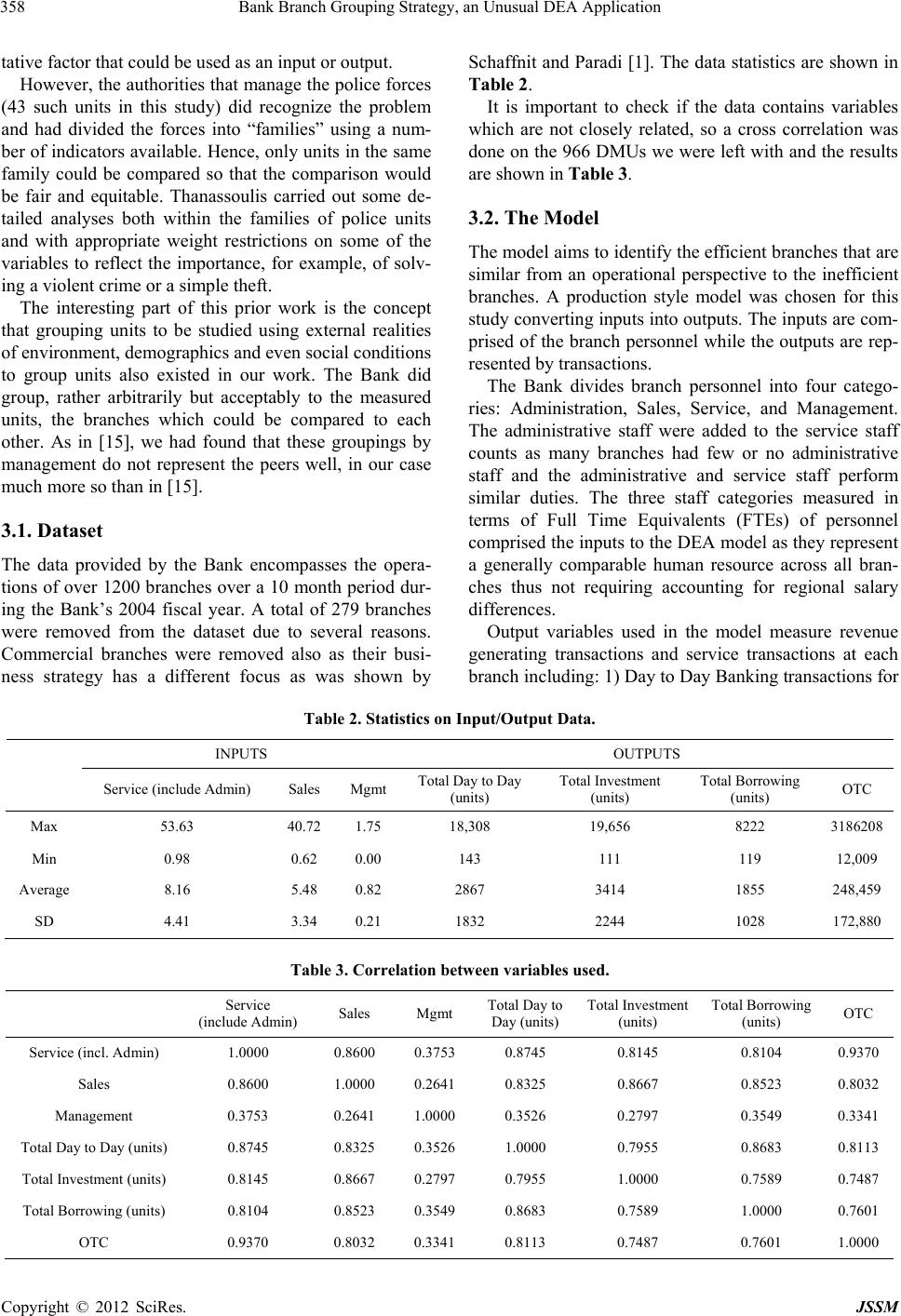

Bank Branch Grouping Strategy, an Unusual DEA Application
358
tative factor that could be used as an input or output.
However, the authorities that manage the police forces
(43 such units in this study) did recognize the problem
and had divided the forces into “families” using a num-
ber of indicators available. Hence, only units in the same
family could be compared so that the comparison would
be fair and equitable. Thanassoulis carried out some de-
tailed analyses both within the families of police units
and with appropriate weight restrictions on some of the
variables to reflect the importance, for example, of solv-
ing a violent crime or a simple theft.
The interesting part of this prior work is the concept
that grouping units to be studied using external realities
of environment, demographics and even social conditions
to group units also existed in our work. The Bank did
group, rather arbitrarily but acceptably to the measured
units, the branches which could be compared to each
other. As in [15], we had found that these groupings by
management do not represent the peers well, in our case
much more so than in [15].
3.1. Dataset
The data provided by the Bank encompasses the opera-
tions of over 1200 branches over a 10 month period dur-
ing the Bank’s 2004 fiscal year. A total of 279 branches
were removed from the dataset due to several reasons.
Commercial branches were removed also as their busi-
ness strategy has a different focus as was shown by
Schaffnit and Paradi [1]. The data statistics are shown in
Table 2.
It is important to check if the data contains variables
which are not closely related, so a cross correlation was
done on the 966 DMUs we were left with and the results
are shown in Table 3.
3.2. The Model
The model aims to iden tify the efficient branches that are
similar from an operational perspective to the inefficient
branches. A production style model was chosen for this
study converting inputs into outputs. The inputs are com-
prised of the branch personnel while the outputs are rep-
resented by transacti ons.
The Bank divides branch personnel into four catego-
ries: Administration, Sales, Service, and Management.
The administrative staff were added to the service staff
counts as many branches had few or no administrative
staff and the administrative and service staff perform
similar duties. The three staff categories measured in
terms of Full Time Equivalents (FTEs) of personnel
comprised the inputs to the DEA model as they represent
a generally comparable human resource across all bran-
ches thus not requiring accounting for regional salary
differences.
Output variables used in the model measure revenue
generating transactions and service transactions at each
branch including: 1) Day to Day Banking transactions for
Table 2. Statistics on Input/Output Data.
INPUTS OUTPUTS
Service (include Admin) Sales MgmtTotal Day to Day
(units) Total Investment (units) Total Borrowing (units) OTC
Max 53.63 40.72 1.75 18,308 19,656 8222 3186208
Min 0.98 0.62 0.00 143 111 119 12,009
Average 8.16 5.48 0.82 2867 3414 1855 248,459
SD 4.41 3.34 0.21 1832 2244 1028 172,880
Table 3. Correlation between variables used.
Service
(include Admin) Sales Mgmt
Total Day to
Day (units) Total Investment (units) Total Borrowing (units) OTC
Service (incl. Admin) 1.0000 0.8600 0.3753 0.8745 0.8145 0.8104 0.9370
Sales 0.8600 1.0000 0.2641 0.8325 0.8667 0.8523 0.8032
Management 0.3753 0.2641 1.0000 0.3526 0.2797 0.3549 0.3341
Total Day to Day (units) 0.8745 0.8325 0.3526 1.0000 0.7955 0.8683 0.8113
Total Investment (units) 0.8145 0.8667 0.2797 0.7955 1.0000 0.7589 0.7487
Total Borrowing (units) 0.8104 0.8523 0.3549 0.8683 0.7589 1.0000 0.7601
OTC 0.9370 0.8032 0.3341 0.8113 0.7487 0.7601 1.0000

Bank Branch Grouping Strategy, an Unusual DEA Application 359
personal and small business accounts; 2) Investments
including personal and small business term-deposits, mo-
ney market funds, fixed income and wealth accounts; 3)
Borrowing consisting of mortgages, personal and small
business loans, lines of credit and credit card balances;
and 4) All over-the-counter (OTC) transaction activity
measured in actual units was also included as an output
variable [11].
The model was formulated as an input oriented BCC
model to assess the potential reduction in staffing levels
at each branch that would allow producing at least the
branches’ current transaction levels. Since the Bank’s
current grouping strategy does not consider the scale of
operations of the branches, the VRS BCC model was
chosen as it accounts for scale effects [9]. For a complete
discussion of the BCC model please refer to the seminal
1984 paper by Banker, Charnes, and Cooper [9].
The BCC multiplier formulation (1) defines a piece-
wise linear convex efficient frontier composed of the best
performing branches [9]. For each bank branch an LP is
solved producing an optimal set of non-negative weights
(ur
* and vi *) that maximize the efficiency score (virtual
output/virtual input ratio) which is restricted to be less
than or equal to 1. The unrestricted variable ũo gives the
model it’s VRS characteristic allowing for the scale
effects to be accounted for in measuring the efficiency of
each bank branch.
1
1
1
1
Max
Subject to1,1,,
0,1,,
0,1, ,
free
s
rro o
r
m
iio
i
s
rrj o
r
m
iij
i
r
i
o
uy u
vx
uy u
jn
vx
urs
vim
u



















(1)
yrj —quantity of the rth (r = 1,···, s) output variable for
unit j (j = 1,···, n);
yro—quantity of the rth output variable for the unit be-
ing evaluated (DMU0);
xij—quantity of the ith (i = 1,···, m) input variable for
unit j (j = 1,···, n);
xio—quantity of the ith input variable for the unit being
evaluated (DMU0);
ur—weight associated with the rth output variable;
vi—weight associated with the ith input variable;
ũo—unrestricted variable that allows for the scale ef-
fects.
The BCC primal multiplier formulation (1) can be
linearized and converted into the BCC dual envelopment
LP formulation as provided below in (2) [9]. The envel-
opment LP formulation (2) is easier to interpret and
reduces the computational effort required to solve it. It
also reports input and output slacks representing the re-
maining possible improvements in a unit’s performance
after the radial improvements have been applied [7]. Any
non-zero values of

j indicate that DMUj is an efficient
DMU referenced by DMU0, or in other words, an ef-
ficient peer to the DMU being evaluated.
11
1
1
1
Min
Subject to,1,,
,1,,
1
,,, 0
sm
ri
ri
n
ioijji
j
n
rorj jr
j
n
j
j
ji r
ss
x
xsi
yysr
ss



























m
s (2)
xij—quantity of the ith (i = 1,···, m) input variable for
unit j (j = 1,···, n);
xio—quantity of the ith input variable for the unit being
evaluated (DMU0);
yrj—quantity of the rth (r = 1, ···, s) output variable for
unit j (j = 1,···, n);
yro—quantity of the rth output variable for the unit be-
ing evaluated (DMU0);

j—weight assigned to unit j;
θ—efficiency score, largest possible proportional in-
puts contraction;
ε—infinitesimal positive number;
i
s

—slack in input variable i;
sr
+—slack in output variable r.
The production model presented in Figure 1 was
solved using the BCC dual envelopment LP formulation
(2). The model was solved through the Saitech Inc’s
DEA-Solver Professional software which utilizes a two
stage approach first solving for θ in Stage 1 and then
fixing θ in Stage 2 and solving for the slacks by max-
imizing their sum [7].
3.3. Peeling Algorithm
One of the perennial problems in DEA studies is the
identification of outliers which may be real or just the
result of some errors in the data. There are a number of
methods to address this issue and we utilize here the
“peeling” approach. In order to produce fair comparisons
between branches, some branches reported as efficient
need to be removed from the dataset as they may operate
in advantageous environments not captured by the

Bank Branch Grouping Strategy, an Unusual DEA Application
360
Figure 1. Model inputs and outputs.
model’s variables, or may posses some advantage which
their peers cannot copy or create. The dataset may also
contain data errors for some branches causing them to be
reported as efficient branches when they are actually not.
Such artificially efficient branches can cause a shift in
the frontier to more efficient levels causing the ineffi-
cient branches referencing those segments of the frontier
thusly distorted to receive unnaturally low efficiency
scores. Such artificially efficient branches could also be
reported as references for inefficient branches when in
fact they are not comparable.
Divine [16], and Thanassoulis [17] suggested using a
layering, or peeling technique, where the efficient units
are removed from the sample and the analysis is run
again to see if the scores of the remaining units change
much. Peeling algorithms are typically based on either
performing several iterations of complete peeling where
all efficient branches are removed during each peel, or
the removal of all efficient branches referenced by more
than a certain threshold of inefficient branches. These
procedures however ignore the strength of these refer-
ences as represented by the λ values.
The final recommendations to the Bank include per-
forming a review of efficient branches that were identi-
fied as potential outliers to determine whether they are
good performers whose results could be achieved by the
branches referenc ing them, or wh ether there is somethin g
unique about their operation s or potentially whether their
data contains an error. However, since it was not plausi-
ble for such a review to be performed by the Bank during
the time that this research was being performed, the peel-
ing algorithm (3) below was used to identify potential
outliers and remove them from the dataset as a precau-
tion.
Sensitivity analysis was used to examine the effects of
removing efficient branches that were being referenced
by an unexpectedly high number of inefficient branches.
The upper threshold level for efficient branches that were
being referenced was set at >25% of the inefficient bran-
ches. The λ values indicate the strength of the relation-
ship between the inefficient branches and the efficient
branches which they reference. When an inefficient
branch is projected onto a point on the BCC efficient
frontier that point is defined as a linear combination of
the efficient branches that the inefficient branch refer-
ences, and those efficient branches’ corresponding λ val-
ues indicate what proportion they contribute to defining
that point on the efficient frontier. Sensitivity analysis
was conducted for λ > 0.15, λ > 0.20, and λ > 0.25 wher e
the efficient branches were being referenced by >25% of
the inefficient branches. As the λ value increased, the
number of times efficient branches were being referenced
decreased as the weaker relationships were not being
counted. Since no efficient branches were being refer-
enced by >25% of the inefficient branches when λ > 0.25,
λ > 0.20 was used to identify which efficient branches to
peel [11]. The peeling algorithm (3) is summarized be-
low.
Peeling algorithm: (3)
Step 1: Solve the production model in Figure 1 using
the BCC envelopment LP Formulation (2).
Step 2: Remove from the dataset all efficient un its ref-
erenced by more than 25% of the inefficient units with a
λ > 0.20.
Step 3: Return to Step 1. Terminate the algorithm once
Step 2 removes no additional efficient outliers.
4. Results
4.1. Peer Group DEA Results
Table 4 summarizes the DEA results broken down by the
Bank’s current peer groups [11]. It should be noted that
group C has the highest number of efficient branches as
it also has the highest number of total branches. Group G
has the second highest number of efficient branches de-
spite having the second lowest total number of branches.
The average efficiency scores were similar across all the
groups.
Using the same model but excluding the 86 branches
from group “G” the same peeling algorithm as previously
discussed was used to remove all efficient outliers that
are being referenced by a significant number of inef-
Table 4. DEA results summary broken dow n by the Bank’s
current peer groups.
Group A B C D E F G Total
# Branches 2992376 129 141 113 86966
# Efficient 4 6 25 6 5 9 1974
% Efficient14% 6%7% 5% 3% 8% 22% 8%
Average Score0.780.810.82 0.81 0.78 0.82 0.82

Bank Branch Grouping Strategy, an Unusual DEA Application 361
ficient units. After the removal of these “rural” bran-
ches and “peeled” units the results are shown in Table 5.
Eleven branches that were considered inefficient previ-
ously became efficient under the new model, but the
percentage of efficient units in the overall branch net-
work remained consistent with the previous analysis. In
addition, the averag e efficiency score did not change sig-
nificantly for each peer group as well as for the overall
network.
4.2. Peer Group Referencing
Since the study aims to examine branches with similar
operating practices, only references of λ > 0.2 were in-
cluded in the analysis, and self-referencing efficient
branches were excluded. A summary of the percentages
of inefficient branches referencing efficient branches
broken down by the Bank’s current peer groups is shown
in Tabl e 6 [11]. Most peer groups (with the exception of
C and G) exhibit relatively low percentages of within
group references suggesting that there may be a high
degree of variability within the group’s operating envi-
ronment—an indication that the Bank’s current grouping
strategy may not be optimal.
All of the Bank’s peer groups frequently referenced
units in groups C and G. Branches in large communities
(A, B, C) referenced the efficient branches in the large
residential communities o f group C at a higher frequency,
while the branches in the smaller communities (D, E, F,
G) refer enced both the efficient branches in group C and
the efficient branches in the small rural communities of
group G at a higher frequency. Group C with the largest
total number of branches (376) and the highest number of
efficient branches (25 out of a total of 74) represents a
diverse set of peers with various operating characteristics
causing them to be benchmarked by many branches in
other peer groups. While group G has the second small-
est number of total branches, it does have the second
highest number of efficient branches, and the highest
percentage of efficient branches, as branches from group
G are generally small branches operating in small rural
communities with small populations. Branches operating
in these environments often have advantageous operating
conditions such as lower staff turnover rates and im-
proved long term relationships with customers.
These observations are consistent with the DEA study
of the retail branch network of a large Canadian Bank
conducted by Schaffnit, Rosen and Paradi [5] where they
found that small community branches were the most ef-
ficient among all peer groups. But while group G does
operate in an advantageous environment, excluding peer
group G from the study produced only small improve-
ments in the within group references rates and did not
lead to a big change in the referencing patterns.
Further analysis was performed by combining groups
Table 5. Efficiency score analysis for all peer groups excluding “G”.
Peer Groups A B C D E F Total
No. of Branches in group 29 92 376 129 141 113 880
No. of Efficient DMUs 4 7 29 6 6 14 66
% of Efficient DMUs (excluding “G”) 14% 8% 8% 5% 4% 12% 7.5%
% of Efficient DMUS with all groups 14% 6% 7% 5% 3% 8% 7.6%
Average Efficiency 0.78 0.82 0.83 0.81 0.79 0.83 0.82
Table 6. Percent of inefficient branches referencing efficient branches.
Efficient Peers
A B C D E F G
A 10% 22% 43% 0% 8% 0% 16%
B 2% 15% 51% 1% 7% 2% 22%
C 3% 17% 48% 3% 11% 3% 15%
D 1% 18% 28% 8% 18% 3% 22%
E 5% 25% 24% 2% 19% 1% 23%
F 0% 7% 28% 2% 28% 8% 26%
Inefficient DMUs
G 0% 5% 24% 2% 6% 6% 56%

Bank Branch Grouping Strategy, an Unusual DEA Application
362
of branches that o perate in similar community sizes. The
combined peer groups are shown in Table 7 [11]. While
these combined groups improved the within group refer-
encing as evidenced by comparing the results from Ta-
bles 6 and 7, there is still a significant percentage of out-
of-group references. The model results therefore show
that branches with similar operating characteristics do
not necessarily operate in the same community settings
and suggest that other factors are influential in determin-
ing peer grouping strategies .
4.3. The Grouping Strategy
The solution proposed to the Bank is to create custom-
ized peer groups for each inefficient branch. While all
efficient references can be provided for each branch, it is
more effective to form smaller peer groups consisting of
the largest λ values since the larger the λ value is, the
more similar the inefficient branch is to the efficient
branch it references. To make the peer groups consistent
and easy to understand and analyze the recommendations
is to provide for each inefficient branch a list of their top
3 efficient reference branches for benchmarking purposes.
Using this approach only 3% of the inefficient branches
had all 3 of their top references in the same peer group;
only 17% of the inefficient branches referenced 2 out of
3 branches from same peer group, and for 40% of the
inefficient branches only 1 out of 3 of their top refer-
ences came from the same peer group. Finally, 40% of
the inefficient branches had all 3 of their top references
come from outside their own peer group.
Since the references produced by DEA are based on
operational similarities, it can therefore be seen that the
Bank’s current grouping strategy fails to cluster opera-
tionally similar branches into the same peer groups, and
benchmarking using the Bank’s currently used grouping
strategy will lead to inappropriate comparisons between
branches and misguided performance improvement tar-
gets.
4.4. Other Factors That Could Affect Peer
Groups
The customized grouping approach is helpful in distin-
guishing characteristics correlated to performance, since
Table 7. References within groups of branches that operate
in similar community sizes.
Clustered Peer Groups References within Clustered
Peer Groups
Large A, B, C 68%
Medium D, E 24%
Small F 8%
Very small rural G 56%
the model completes a comprehensive analysis to form
peer groups. Nevertheless, there are other factors that
may exploit the multidimensional modeling capability of
DEA, such as: staff experience, demographics, location
and competition to name a few. Clearly, these factors
have influence on performance, but data is almost never
available to address these questions.
Staff experience could be measured as the length of
employment and training levels received. More experi-
enced staff may have better developed skills or may be
more familiar with customer needs which tend to in-
crease efficiency (rural branches). On the other hand,
branches experiencing relatively high turnover as com-
pared to other peers may require more time and effort to
train the new employees, thus differentiating these bran-
ches (large urban locations). But such data was no t avail-
able to us, nor is it likely to be released even if the Bank
had it, citing privacy issues.
Canada has a comprehensive database of census in-
formation that is publicly available. Using this data, we
could try to understand which, if any, demographic fac-
tors have significant effects on branch productivity. For
example, transactions may be completed more efficiently
if barriers to communication are minimized—Canada is a
highly multi-cultural society with a significant number of
residents with poor or non-existent comman d of the Eng-
lish language1. In fact, the Bank can and does staff the
branches to meet local language needs, but this does not
solve the whole problem. Another factor may be related
to usage of online resources (e.g. Web Banking) which
would be difficult for computer illiterate customers, who
then will go to the branch and create additional transac-
tions.
Bank branches located within readily accessible facili-
ties might not be a good comparison for those that are not
centrally located. Branches located in shopping centres,
for example, may service more inter-bank2 customers as
compared to less accessible branches. Operating charac-
teristics are often influenced by the customer mix and
accessibility of the branch.
Peer groups may also be formed using local competi-
tion intensity or lack thereof as parameters. If there is
relatively less competition, there may be more opportun i-
ties for new account activities since customers do not
have the option to bank with other financial institutions.
As a result, such branches may inherently have an ad-
vantage in increasing their sales outputs to make them
more efficient.
1This does not imply that branches in neighborhoods that are not pre-
dominantly English speaking are nece ss ar il y le ss e fficient.
2Inter-
b
ank customers are customers who do not have an account at the
Bank. Process times are longer for these customers for due-diligence
and a
pp
rovals re
qu
ired for identit
y
verification.

Bank Branch Grouping Strategy, an Unusual DEA Application 363
5. Conclusions
In today’s competitive banking environment operational
efficiency of the Bank’s branch network is critical to its
success. Branch performance is often difficult to evaluate,
primarily due to the complexity of their operations. To
evaluate operational (not profitability, etc.) branch effi-
ciency, the Bank must first cluster them into meaningful
peer groups so that branches could be compared and
evaluated against each other in a clearly fair and equita-
ble manner. This study evaluated the current grouping
methodology employed by the Bank, which is based on
community type and population size. The bank branches’
peer groups were compared to the reference sets pro-
duced by the input oriented DEA BCC production model
that used personnel FTE levels as inputs and customer
transactions as outputs.
A peeling algorithm was used to eliminate potential
outliers. This approach was conservatively applied in
order to avoid the elimination of good reference DMUs
that the inefficient branches could learn from. It is re-
commended that the Bank review the data for every po-
tential outlier iden tified through the peeling procedure to
determine if it is, in fact, an outlier. The potential outlier
identification thresholds could be lowered further to
identify a larger group of potential outliers for the Bank
to review.
The analyses based on the DEA results indicated that
most of the efficient branches being referenced came
from outside of the inefficient branches’ peer groups as
those were defined by the Bank, suggesting that opera-
tional similarity is not generally related to community
type and population size. This result suggests that there
may be a high degree of variability within the Bank de-
fined peer groups’ operating environments, and that op-
erational similarities exist between branches across peer
groups leading to cross referencing at high frequencies.
The small rural community branches of group G were
referenced by the highest percentage of inefficient units
in other peer groups relative to the total number of
branches in group G, as group G exhibits unique operat-
ing conditions such as lower staff turn over rates and
long term customer relationships. A subsequent analysis
was performed to examine possible bias introduced into
the model by the group G branches, but the model with-
out the rural group G branches exhibited the same trends
as the model using the entire dataset showing a high fre-
quency of out-of-group referencing again suggesting that
branches in different peer groups might, in fact, share
comparable and similar operational characteristics.
Using the DEA model’s results, it is recommended
that for each inefficient branch a customized peer group
be identified consisting of its top 3 references based on
the highest λ values. Consistent with the Bank’s goal of
having a truly comprehensive grouping strategy, the
proposed model captures the combined effects of various
inputs and outpu ts not readily iden tifiable with its current
grouping strategy. This approach yields a set of fair and
equitable groups that compare inefficient branches to
their most operationally similar efficient peers. By pro-
viding up to 3 unique, best practice efficient peers for
each inefficient branch, meaningful comparisons can be
made to identify the best practices that could be imple-
mented by the inefficient branches to improve their per-
formance. This approach is intuitiv e and simple for Bank
staff to adopt, thus increasing the probability of a suc-
cessful implementation.
Additional research and a review of the results by the
Bank is required in order to ensure that the references are
valid and that no unaccounted for advantages exist caus-
ing some branches to appear to be artificially efficient.
Should such factors exist, the Bank should provide the
relevant data so that these factors could be accounted for
in the model.
REFERENCES
[1] J. C. Paradi and C. Schaffnit, “Commercial Branch Per-
formance Evaluation and Results Communication in a
Canadian Bank—A DEA Application,” European Jour-
nal of Operational Research, Vol. 156, No. 3, 2004, pp.
719-735. doi:10.1016/S0377-2217(03)00108-5
[2] J. C. Paradi, S. Vela and Z. Yang, “Assessing Bank and
Bank Branch Performance: Modeling Considerations and
Approaches,” In: W. W. Cooper, L. M. Seiford and J. Zhu,
Eds., Handbook on Data Envelopment Analysis, Kluwer
Academic Publishers, Boston, 2004, pp. 349-400.
[3] D. McEachern and J. C. Paradi, “Intra- and Inter-Country
Bank Branch Performance Assessment Usi ng DEA,” Jour-
nal of Productivity Analysis, Vol. 27, No. 2, 2007, pp. 123-
136. doi:10.1007/s11123-006-0029-z
[4] Z. J. Yang and J. C. Paradi, “Crossfirm Bank Branch
Benchmarking Using ‘Handicapped’ Data Envelopment
Analysis to Adjust for Corporate Strategic Effects,” Pro-
ceedings of the 39th Hawaii International Conference on
System Sciences, Kauai, 4-7 January 2006.
[5] C. Schaffnit, D. Rosen and J. C. Paradi, “Best Practice
Analysis of Bank Branches: An Application of DEA in a
Large Canadian Bank,” European Journal of Operational
Research, Vol. 98, No. 2, 1997, pp. 269-289.
doi:10.1016/S0377-2217(96)00347-5
[6] Canadian Bankers Association, “Our Industry,” 2006.
http://www.cba.ca/en/industry.asp
[7] W. W. Cooper, L. M. Seiford and K. Tone, “Data Envel-
opment Analysis: A Comprehensive Text with Models,
Applications, References, and DEA-Solver Software,”
Kluwer Academic Publishers, Boston, 2000.
[8] A. Charnes, W. W. Cooper and E. L. Rhodes, “Measuring
the Efficiency of Decision Making Units,” European Jour-
nal of Operational Research, Vol. 2, No. 6, 1978, pp. 429-
444. doi:10.1016/0377-2217(78)90138-8
[9] R. D. Banker, A. Charnes and W. W. Cooper, “Some

Bank Branch Grouping Strategy, an Unusual DEA Application
364
Models for Estimating Technical and Scale Inefficiencies
in Data Envelopment Analysis,” Management Science,
Vol. 30, No. 9, 1984, pp. 1078-1092.
doi:10.1287/mnsc.30.9.1078
[10] H. D. Sherman and F. Gold, “Bank Branch Operating Ef-
ficiency: Evaluation with Data Envelopment Analysis,”
Journal of Banking and Finance, Vol. 9, No. 2, 1985, pp.
297-316. doi:10.1016/0378-4266(85)90025-1
[11] P. Yom and A. Wu, “Bank Branch Logical Grouping
Strategy,” BASc Thesis, University of Toronto, Toronto,
2006.
[12] Statistics Canada, “1996 Community Profiles,” 1996
Census, 1999.
http://www12.statcan.ca/english/profil/PlaceSearchForm1
.cfm?LANG=E
[13] Statistics Canada, “2001 Community Profiles,” 2001
Census, 2001.
http://www12.statcan.ca/english/profil01/CP01/Index.cfm
?Lang=E
[14] Statistics Canada, “2006 Community Profiles,” 2006
Census, 2007.
http://www12.statcan.ca/english/census06/data/profiles/co
mmunity/Index.cfm?Lang=E
[15] E. Thanassoulis, “Assessing Police Forces in England and
Wales Using Data Envelopment Analysis,” European Jour-
nal of Operational Research, Vol. 87, No. 3, 1995, pp.
641-657. doi:10.1016/0377-2217(95)00236-7
[16] J. D. Divine, “Efficiency Analysis and Management of
Not for Profit and Governmentally Regulated Organiza-
tions,” Ph.D. Thesis, University of Texas, Austin, 1986.
[17] E. Thanassoulis, “Setting Achievements Target s for School
Children,” Education Economics, Vol. 7, No. 2, 1999, pp.
101-119. doi:10.1080/09645299900000010