Communications and Network, 2010, 2, 193-199
doi:10.4236/cn.2010.23028 Published Online August 2010 (http://www.SciRP.org/journal/cn)
Optimization of UMTS Network Planning Using Genetic
Algorithms
Fabio Garzia, Cristina Perna, Roberto Cusani
INFOCOM Department, SAPIENZA – Uni versi t y of Rome , Rome, Ital y
Received May 8, 2010; revised June 8, 2010; accepted June 20, 2010
Abstract
The continuously growing of cellular networks complexity, which followed the introduction of UMTS tech-
nology, has reduced the usefulness of traditional design tools, making them quite unworthy. The purpose of
this paper is to illustrate a design tool for UMTS optimized net planning based on genetic algorithms. In par-
ticular, some utilities for 3G net designers, useful to respect important aspects (such as the environmental
one) of the cellular network, are shown.
Keywords: UMTS Network Planning, Genetic Algorithms
1. Introduction
The extraordinary growth of mobile telecommunication
sector of the last years has implied strong economical
investments of enterprises that operate in this vital sector,
in particular way from the net infrastructure point of
view.
The development of third generation mobile commu-
nication (3G) such as UMTS, with the related advanced
allowed services, has increased the need of an efficient
network planning that could keep into account all the
aspects of complexity which are typical of this new
technology, changing the traditional approach to this
kind of problem [1-3].
In fact, even if the WCDMA techniques used by
UMTS reduce the problems related to the frequency
management, the capacity of the net represents a vital
problem since the capacity of each radio cell is strongly
related to the signal – interference ratio (SIR), that is a
function of the number and of the kind of active users
inside each communication cell [2,3].
The need of reduction of radiated power, due to envi-
ronmental restrictions, and the need of guaranteeing a
good quality of services, requires a capillary distribution
of Radio Base Stations (BSs) on the territory to be covered.
Nowadays, due to the reduced availability of BSs place-
ment zones, it is necessary to seek new and efficient
methods to optimize the cellular coverage services.
Different and interesting solutions have already been
proposed. One of the most interesting is based on a tech-
nique inspired to the natural evolution, represented by
the Genetic Algorithms (GAs) [4-21], which are good
candidates, thank s to their versatility, to solve a co mplex
and multi-parametric problem such as the considered
one.
The purpose of this work is to illustrate a new GAs
based method to solve the optimization coverage and
capacity problem of UMTS system, keeping into account
its specific features and the typical restrictions found in
real situations, such as the environmental one.
2. The Genetic Algorithms
Genetic algorithms are considered wide range numerical
optimisation methods which use the natural processes of
evolution and genetic recombination. Thanks to their
versatility, they can be used in different application fields.
The algorithms encode each parameters of the problem
to be optimised into a proper sequence (where the
alphabet used is generally binary) called a gene, and
combine the different genes to constitute a chromosome.
A proper set of chromosomes, called population, under-
goes the Darwinian processes of natural selection, mating
and mutation, creating new generations, until it reaches
the final optimal solution under the selective pressure of
the desired fitness function.
GA optimisers, therefore, operate according to the
following nine points :
1) encoding the solution parameters as genes;
2) creation of chromosomes as strings of genes;
3) initialisation of a starting population;
4) evaluation and assignment of fitness values to the

F. GARZIA ET AL. 194
individuals of the population;
5) reproduction by means of fitness-weighted selection
of individuals belonging to the population;
6) recombination to produce recombined members;
7) mutation on the recombined members to produce
the members of the next generation.
8) evaluation and assignment of fitness values to the
individuals of the next generation;
9) convergence check.
The coding is a mapping from the parameter space to
the chromosome space and it transforms the set of
parameters, whi ch is generall y composed by real num bers,
in a string characterized by a finite length. The parameters
are coded into genes of the chromosome that allow the
GA to evolve i ndepe ndentl y of the pa rame ters them selves
and therefore of the solution space.
Once created the chromosomes it is necessary choose
the number of them which composes the initial popula-
tion. This number strongly influences the efficiency of
the algorithm in finding the optimal solution: a high
number provides a better sampling of the solution space
but slow s the convergence.
Fitness function, or cost function, or object function
provides a measure of the goodness of a given chromo-
some and therefore the goodness of an individual within
a population. Since the fitness function acts on the
parameters themselves, it is necessary to decode the
genes composing a given chromosome to calculate the
fitness function of a certain individual of the population.
The reproduction takes place utilising a proper selec-
tion strategy which uses the fitness function to choose a
certain number of good candidates. The individuals are
assigned a space of a roulette wheel that is proportional
to they fitness: the higher the fitness, the larger is the
space assigned on the wheel and the higher is the prob-
ability to be selected at every wheel tournament. The
tournament process is repeated until a reproduced popu-
lation of N individuals is formed.
The recombination process selects at random two
individuals of the reproduced population, called parents,
crossing them to generate two new individuals called
children. The simplest technique is represented by the
single-point crossover, where, if the crossover probability
overcome a fixed threshold, a random location in the
parent’s chromosome is selected and the portion of the
chromosome preceding the selected point is copied from
parent A to child A, and from parent B to child B, while
the portion of chromosome of parent A following the
random selected point is placed in the corresponding
positions in child B, and vice versa for the remaining
portion of pa rent B chrom oso me.
If the crossover probability is below a fixed threshold,
the whole chromosome of parent A is copied into child A,
and the same happens for parent B and child B. The
crossover is useful to rearrange genes to produce better
combinations of them and therefore more fit individuals.
The recombination process h as shown to be very import an t
and it has been found that it should be applied with a
probability varying between 0.6 and 0.8 to obtain the
best results.
The mutation is used to survey parts of the solution
space that are not represented by the current population.
If the mutation probability overcomes a fixed threshold,
an element in the string composing the chromosome is
chosen at random and it is changed from 1 to 0 or vice
versa, depending of its initial value. To obtain good
results, it has been shown [4] that mutations must occur
with a low probability varying between 0.01 and 0.1.
The converge check can use different criteria such as
the absence of further improvements, the reaching of the
desired goal or the reaching of a fixed maximum number
of generations.
3. Definition of the Problem
It is evident that, thanks to their versatility, GAs represent
good candidates to solve the typical optimization problem
of UMTS cellular net planning.
GAs have already been used for this kind of problem
[5-21], even if their application is limited only to terri-
tory coverage. On the contrary, in this paper, other
parameters (such as SIR), that strongly influence the
results in real situations, are considered, generating a
powerful tool for optimal net planning.
Some general criteria have been adopted, without re-
ducing the generality of the problem, which are:
1) it has been considered a suburban area whose
dimensions are 3 km x 3 km with an inhomogeneous
traffic distribution, even if the proposed algorithm is
suitable for different shaped areas;
2) high gain BSs, placed at the same height, are con-
sidered;
3) circular irradiation diagrams of BSs, instead of
three-lobes diagrams, are considered. This assumption,
made to simplify the implementation of the algorithm,
does not influence the final result;
4) a consolidated electromagnetic propagation model
[22] has been adopted;
5) the SIR has been calculated using the following
formula [3]:
r
in out
P
SIRSF IIη 

(1)
Figure 1. Operation scheme of a GA iteration.

F. GARZIA ET AL.195
where SF is the Spreading Factor, Pr is the received
power, Iin is the intra-cells interference, Iout is the in-
ter-cells interference, η is the thermal noise.
4. Proposed Algorithms for Optimization
Problem
Since a plenty of goals and restrictions must be respected
in a UMTS net, the design can be made following dif-
ferent criteria.
The designer can therefore have different optimization
tools that allow him to consider, in each real situation,
the predominant aspects.
For this reason, in this paper, the different mentioned
real situations have been considered, showing the great
flexibility of the proposed method.
4.1. Case 1
A situation without information about traffic level,
without restrictions about the maximum number of BSs
that can be used and without restrictions about their ter-
ritorial placement is considered.
The goal of this case is the optimization of territorial
coverage, neglecting the performance of the service as-
pects.
To reach this target it is necessary to find a proper fit-
ness function of GA and a proper chromosome.
The BSs are coded, inside the chromosome, by means
of 2 double vectors, that represents the coordinates of
each BS on the territory. To determine the length of the
chromosome, related to the number of considered BSs,
the minimum number of BSs necessary to ensure the
coverage of a given percentage pT of the territory, is
calculated as:
minTTot BSn_bspA C

 
(2)
where ATot represents the area of the considered territory;
pT is the percentage of territory that must be covered; CBS
is the maximum coverage area of each BSs.
Due to the usual not regular sh ap e of the territory to be
covered and to the impossibility of perfectly matching
the coverage diagram of near BSs, the value calculated
by means of (2) may be not sufficient and it is necessary
to consider a proper multiple n, generally equal to two.
In the considered situation, we have n_bsmin=23.
Each gene of the chromosome, representing a BSs, is
composed by a number k of variables equal to 3: 2 are
used for the position of the BSs on the territory and 1 is
used to represent the state of activation /deactivation of
the BSs.
The length λ of the chromosome (in term of number of
variables) in the considered situation is expressed by the
following formula:
minλ nn_bsk  (3)
Substituting the numerical values, we have: λ= 138.
The fitness function (Ffit) to minimize is, in this situa-
tion:
Tot CovL
fit Tot Totmin
A
- AOn_bs
Fαβγ
A
An n_bs
  (4)
where ACov is the sum of the coverage areas of the BSs
placed on the territory, OL is the sum of the superposition
areas of radiation diagram of BSs, n_bs is the number of
BSs placed on the territory, α, β and γ are weight coeffi-
cients that are varied as a function of the project goals.
4.2. Case 2
In real situations, the traffic inside a territory is not dis-
tributed in a homogeneous way. The concentration users
zones are named hot spots. It is evident that, to guarantee
a certain QoS level, it is necessary to reduce, as more as
possible, the intra-cells and inter-cells interference. As a
consequence, placing a BS in a hot spot represents a first
significant step in net optimizatio n.
Given a non homogeneous traffic distribution and an
initial numbers of BSs, calculated according to (2), the
algorithm is capable of maximizing coverage and capacity
and of minimizing cost.
The fitness function to minimize in this case is:
f
TotCovLTot Cov
TotTotmin Tot
F
A
- AOn_bsU-U
αβγ δ
AAnn_bsU

 

(5)
where UTot is the number of estimated users inside the
territory and UCov is the number of users covered by the
active BSs.
4.3. Case 3
In real situation, for environmental reasons, it is not
po ssible to place BSs anywhere. In this case, only a lim-
ited number of zones is available and it is necessary to
find a function that accepts, as inputs, not only informa-
tion concerning traffic but also information concerning
the available installation zones (in particular their coor-
dinates). The function must optimize the net considering
these limitations that is a cost vinculum. Its structure is
therefore equal to the one of (5) less the cost factor.
4.4. Case 4
Another crucial factor in UMTS system is represented by
the radiated power (environmental restrictions), with
particular respect to the QoS. Therefore the net needs,
sometimes, to place the BSs on the territory to reduce, as
more as possible, the emitted power, guaranteeing an
acceptable level of QoS.
In this case the power of each BS is considered as in-

F. GARZIA ET AL. 196
put parameter (which can be properly changed), that in-
fluences not only the coverage area but also the trans-
mission capacity.
The fitness function is therefore:
f
TotCovLTotTot Cov
TotTotMax Tot
F
A
-AOPU -U
αβγ δ
AAn_srb PU

 

(6)
where PTot is the total power of BSs and PMax in the
maximum power radiated by each BS.
5. Performance of the Algorithms and
Results
In the following the results of each situation considered
above are shown.
5.1. Case 1
Purpose of case 1 is the optimization of the net consider in g
only the coverage of the territory, keeping into account
the cost factor. The results obtained are shown in the
following.
A first situation has been obtained considering the
following values for the weights of fitness function: α =
0.6, β=0.1, γ=0.3. The results are shown in Figure 2. It is
possible to see that the presence of a strong cost compo-
nent has heavily penalized the coverage maximization.
A second situation has been obtained considering the
following values for the weights of fitness function α=1,
β=0, γ=0, that is to maximize coverage considering the
cost as a quasi-neglectable factor.
Due to the structure of fitness func tion, it always tends
to limit the number of BSs on the territory, evaluating
each time if the coverage gain justify the increase of the
number of BS s.
(a)
(b)
Figure 2 (a) Initial situation. Units are expressed in kilo-
meters. (b) Final results after 300 generations. Units are
expressed in kilo-meters.
(a)
(b)
Figure3 (a) Initial situation. Units are expressed in kilo-
meters. (b) Final results after 300 generations. Units are
expressed in kilo-meters.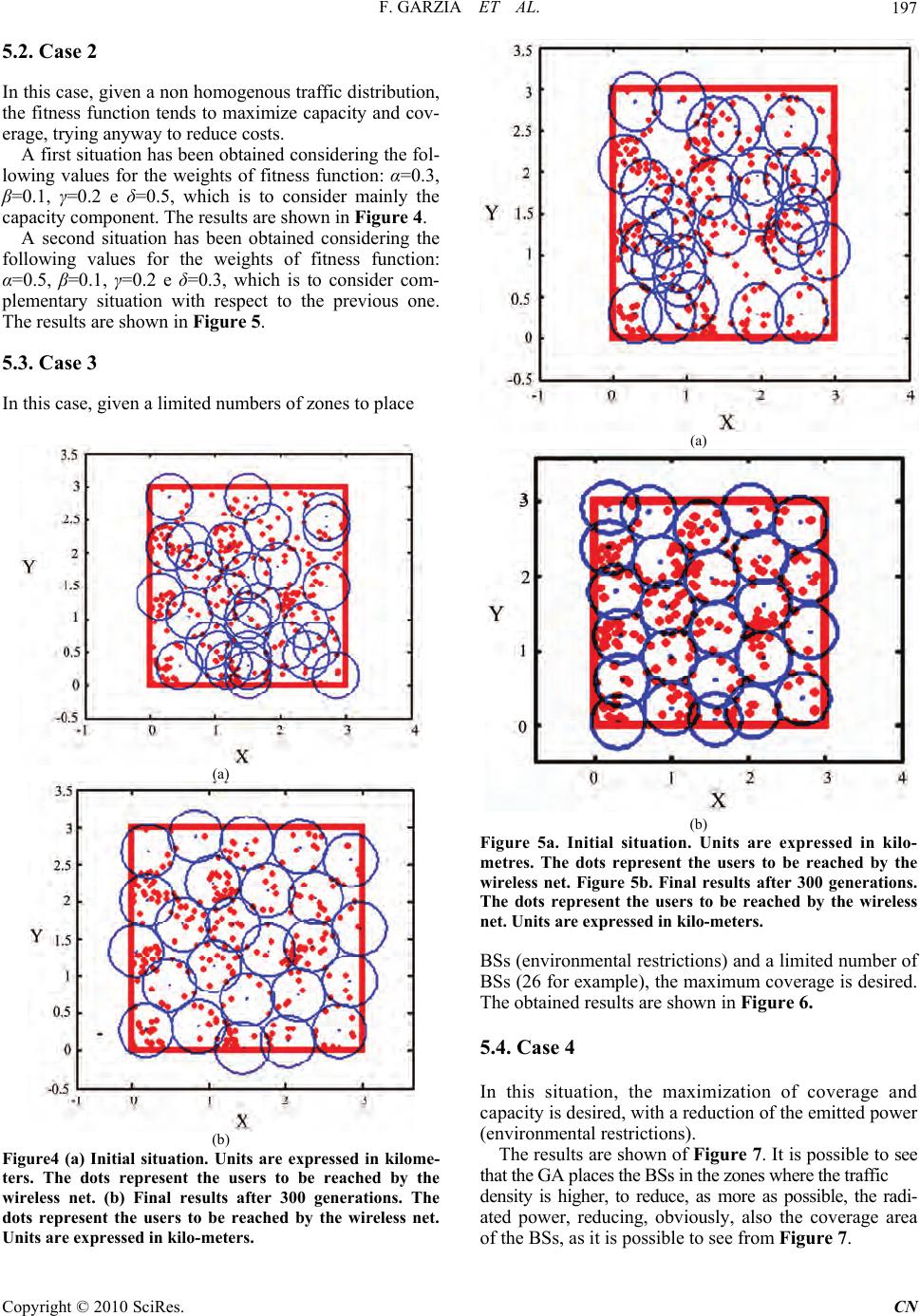

F. GARZIA ET AL.197
5.2. Case 2
In this case, given a non homogenous traffic distribution,
the fitness function tends to maximize capacity and cov-
erage, trying anyway to reduce costs.
A first situation has been obtained considering the fol-
lowing values for the weights of fitness function: α=0.3,
β=0.1, γ=0.2 e δ=0.5, which is to consider mainly the
capacity component. The results are shown in Figure 4.
A second situation has been obtained considering the
following values for the weights of fitness function:
α=0.5, β=0.1, γ=0.2 e δ=0.3, which is to consider com-
plementary situation with respect to the previous one.
The results are shown in Figure 5.
5.3. Case 3
In this case, given a limited numbers of zones to place
(a)
(b)
Figure4 (a) Initial situation. Units are expressed in kilome-
ters. The dots represent the users to be reached by the
wireless net. (b) Final results after 300 generations. The
dots represent the users to be reached by the wireless net.
Units are expressed in kilo-meters.
(a)
(b)
Figure 5a. Initial situation. Units are expressed in kilo-
metres. The dots represent the users to be reached by the
wireless net. Figure 5b. Final results after 300 generations.
The dots represent the users to be reached by the wireless
net. Units are expressed in kilo-meters.
BSs (environmental restrictions) and a limit ed number of
BSs (26 for example), the maximum coverage is desired.
The obtained results are shown in Figure 6.
5.4. Case 4
In this situation, the maximization of coverage and
capacity is desired , with a redu ction of the emit ted power
(environmental restrictions).
The results are shown of Figure 7. It is possible to see
that the GA places the BSs in the zones where the traffic
density is higher, to reduce, as more as possible, the radi-
ated power, reducing, obviously, also the coverage area
of the BSs, as it is possible to see from Figure 7.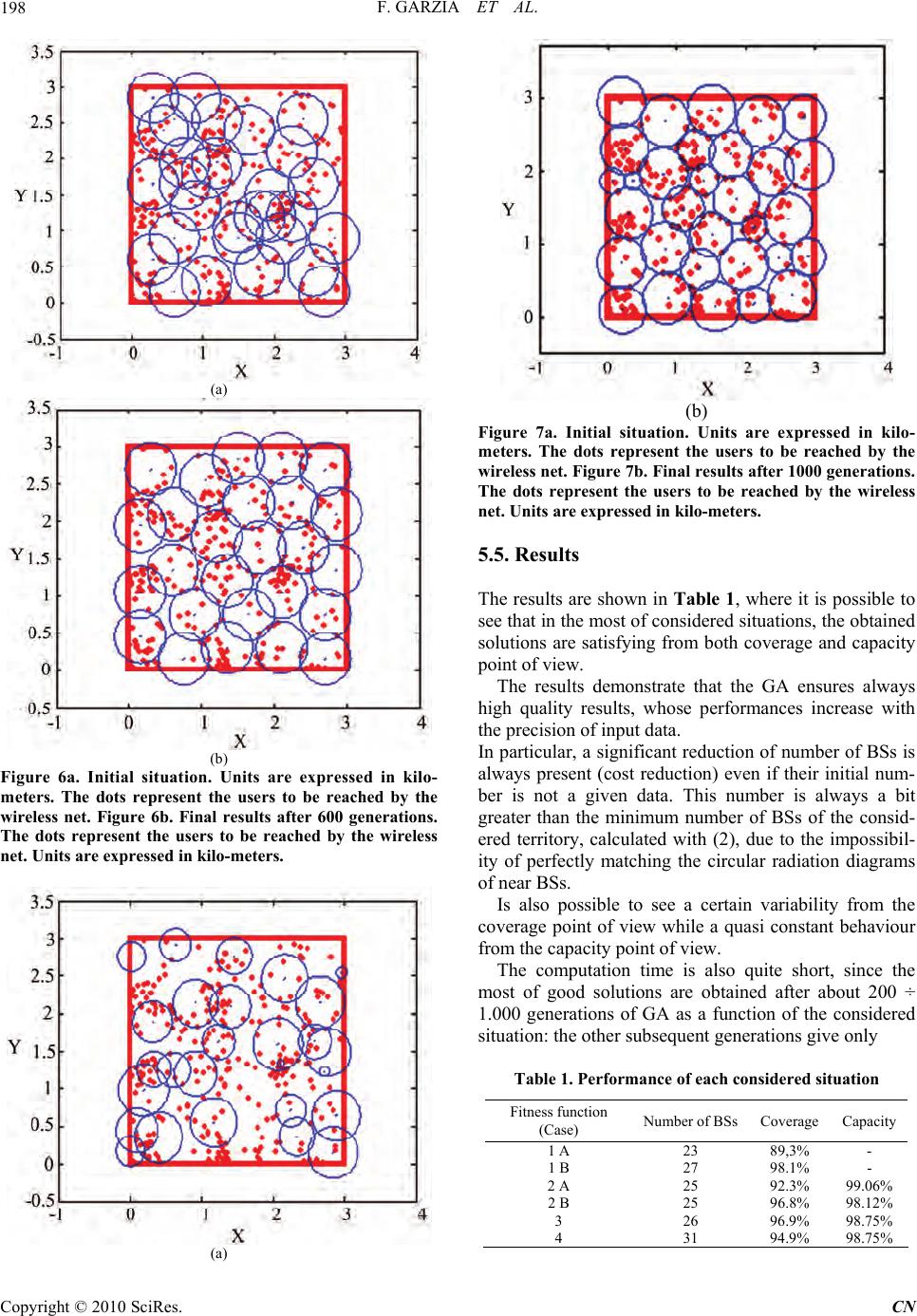

F. GARZIA ET AL. 198
(a)
(b)
Figure 6a. Initial situation. Units are expressed in kilo-
meters. The dots represent the users to be reached by the
wireless net. Figure 6b. Final results after 600 generations.
The dots represent the users to be reached by the wireless
net. Units are expressed in kilo-meters.
(a)
(b)
Figure 7a. Initial situation. Units are expressed in kilo-
meters. The dots represent the users to be reached by the
wireless net. Figure 7b. Final results after 1000 generations.
The dots represent the users to be reached by the wireless
net. Units are expressed in kilo-meters.
5.5. Results
The results are shown in Table 1, where it is possible to
see that in the most of considered situations, the obtain ed
solutions are satisfying from both coverage and capacity
point of view.
The results demonstrate that the GA ensures always
high quality results, whose performances increase with
the precision of input data.
In particular, a significant reduction of number of BSs is
always present (cost reduction) even if their initial num-
ber is not a given data. This number is always a bit
greater than the minimum number of BSs of the consid-
ered territory, calculated with (2), due to the impossibil-
ity of perfectly matching the circular radiation diagrams
of near BSs.
Is also possible to see a certain variability from the
coverage point of view while a quasi constant behaviour
from the capacity point of view.
The computation time is also quite short, since the
most of good solutions are obtained after about 200 ÷
1.000 generations of GA as a function of the considered
situation: the other subsequent generations give only
Table 1. Performance of each considered situation
Fitness function
(Case) Number of BSs Coverage Capacity
1 A 23 89,3% -
1 B 27 98.1% -
2 A 25 92.3% 99.06%
2 B 25 96.8% 98.12%
3 26 96.9% 98.75%
4 31 94.9% 98.75%

F. GARZIA ET AL. 199
little improvement of qu ality of solutions.
7. Conclusions
A genetic algorithm based technique to optimize the de-
sign of UMTS cellular nets has been presented.
The proposed method considers most of the limits im-
posed by the installation of the BSs necessary to guarantee
an optimal service, also including environmental restric-
tions.
Even if some simplifications were made, the considered
technique is capable of ensuring good results from any
point of view, representing a useful too l for UMTS initial
optimization.
8. References
[1] J. C. S. Cheung, M. A. Beach and J . McGeehan, “Netw ork
Planning for Third-generation Mobile Radio Systems,”
IEEE Communications Magazine, Vol. 32, No. 11, No-
vember 1994, pp. 54-59
[2] E. Berruto, M. Gudmundson, R. Menolascino, W.Mohr,
and M. Pizarroso, “Research Activities on UMTS Radio
Interface, Network Architectures, and Planning,” IEEE
Communications Magazine, Vol. 36, No. 2, February
1998, pp. 82-95.
[3] E. Amaldi, A. Capone and F. Malucelli, “Planning UMTS
Base Station Location: Optimization Models With Power
Control and Algorithms,” IEEE Transactions on Wireless
Communications, Vol. 2, No. 5, September 2003, pp.
939-952.
[4] D. E. Goldberg, “Genetic Algorithms in Search, Optimiza-
tion and Machine Learning,” Addison Wesley, Massa-
chusetts, 1989.
[5] L. Nagi and L. Farkas, “Indoor Base Station Location
Optimization Using Genetic Algorithms,” IEEE Interna-
tional Symposium on Personal, Indoor and Mobile
Communications, Vol. 2, London, 2000, pp. 843-846.
[6] B. Di Chiara, R. Sorrentino, M. Strappini and L. Tarrico ne,
“Genetic Optimization of Radio Base-station Size and
Location Using a GIS-based Frame Work: Experimental
Validation,” IEEE International Symposium of Antennas
and Propagation Society, Vol. 2, 2003, pp. 863-866.
[7] J. K. Han, B. S. Park, Y. S. Choi, and H. K. Park,
“Genetic Approach with a New Representation for Base
Station Placement in Mobile Communications,” IEEE
Vehicular Technology Conference, Vol. 4, No. 54ND,
2001, pp. 2703-2707.
[8] R. Danesfahani, F. Razzazi and M. R. Shahbazi, “An
Active Contour Based Algorithm for Cell Planning,”
IEEE International Conference on Communications
Technology and Applications, Beijing, 2009, pp. 122-126.
[9] R. S. Rambally and A. Maharajh, “Cell Planning Using
Genetic Algorithm and Tabu Search,” International Con-
ference on the Application of Digital Information and
Web Technologies, 2009, pp. 640-645.
[10] K. Lieska, E. Laitinen and J. Lahteenmaki, “Radio
Coverage Optimization with Genetic Algorithms,” IEEE
International Symposium on Personal, Indoor and Mobile
Radio Communications, Vol. 1, 1998, pp. 318-322.
[11] A. Esposito, L. Tarricone and M. Zappatore, “Software
Agents: Introduction and Application to Optimum 3G
Network Planning,” IEEE Antennas and Propagation
Magazine, 2009, pp. 147-155.
[12] L. Shaobo, P. Weijie, Y. Guanci and C. Linna, “Optimi-
zation of 3G Wireless Network Using Genetic Program-
ming,” International Symposium on Computational Intel-
ligence and Design, Vol. 2, 2009, pp.131-134.
[13] C. Maple, G. Liang and J. Zhang, “Parallel Genetic
Algorithms for Third Generation Mobile Network Plan-
ning,” International Conference on Parallel Computing in
Ele ctrical Engineering, Dresden, 2004, pp. 229-236.
[14] I. Laki, L.Farkas and L. Nagy, “Cell Planning in Mobile
Communication Systems Using SGA Optimization,”
International conference on Trends in Communications,
Vol.1, 2001, pp.124-127.
[15] D. B. Webb, “Base Station Design for Sector Coverage
Using a Genetic Algorithm with Method of Moments,”
IEEE International Symposium of Antennas and Propa-
gation Society, Vol.4, 2004, pp. 4396-4399.
[16] A. Molina, A. R. Nix, and G. E. Athanasiadou, “Opti miz ed
base-station location algorithm for next generation mi-
crocellular networks,” Electronics Letters, Vol.36, No. 7,
2000, pp. 668-669.
[17] G. Cerri, R. De Leo, D. Micheli, and P. Russo,
“Base-station network planning including environmental
impact control,” IEEE Proceedings on Communications,
Vol. 151, No. 3, 2004, pp. 197-203.
[18] A. Molina, G. E. Athanasiadou and A. R. Nix, “The Auto-
matic Location of Base-stations for Optimized Cellular
Coverage: A New Combinatorial Approach,” IEEE In-
ternational Conference on Vehicular Technology, Vol. 1,
1999, pp. 606-610.
[19] N. Weaicker, G. Szabo, K. Weicker and P. Widmayer,
“Evolutionary Multi-objective Optimization for Base Sta-
tion Transmitter Placement with Frequency Assignment,”
IEEE Transactions on Evolutionary Computations, Vol.7,
No. 2, 2003, pp.189-203.
[20] G. Fangqing, L. Hailin and L. Ming, “Evolutionary Algo-
rithm for the Radio Planning and Coverage Optimization
of 3G Cellular Networks,” International Conference on
Computational Intelligence and Security, Vol.2, Wash-
ington, D. C., 2009, pp. 109-113.
[21] J. Munyaneza, A. Kurine and B. Van Wyk, “Optimization
of Antenna Placement in 3G Networks Using Genetic
Algorithms,” International Conference on Broadband
Communications, Information Technology & Biomedical
Applications, 2008, pp. 30-37.
[22] M. Hata, “Empirical Formula for Propagation Loss in
Land Mobile Radio Services,” IEEE Transactions on
Vehicular Technology, Vol. VT-29, No. 3, 1980, pp.
317-325.