J. Serv. Sci. & Management, 2009, 2: 10-14
Published Online March 2009 in SciRes (www.SciRP.org/journal/jssm)
Performance Evaluation Model of Engineering Project
Management Based on Improved Wavelet Neural Network
Qinghua Zhang
1
, Qiang Fu
1,2
1
College of Water Conservancy and Civil Engineering, Northeast Agricultural University, Harbin China,
2
Visiting Scientist, Depart-
ment of Renewable Resources, University of Alberta, Edmonton, T6G2E3, Canada.
Received October 8
th
, 2008; revised January 20
th
, 2009; accepted February 16
th
, 2009.
ABSTRACT
The scientific and reasonable performance evaluation is advantageous to promote the comprehensive management level
of engineering projects. Benefited from constrictive and fluctuant of wavelet transform and self-study, self-adjustment
and nonlinear mapping functions of wavelet neural network (WNN), and based on the existing assessment method and
the index system, the performance evaluation model of engineering project management is established. One company is
taken as the study object for this model. Compared with the conventional method, the influence of human factor is
eliminated, thus the objectivity of the measure results is increased. A satisfactory result is concluded, thus a new ap-
proach is presented for engineering project management performance evaluation.
Keywords: wavelet neural network, entropy function, project management, performance evaluation
1. Introduction
Project management is the systematic analysis and ob-
jective evaluation for the management of completed
projects. It can put forward some suggestions for the
future management and improving decision-making
levels. Scientific and rational project management per-
formance evaluation is conducive to improve the level
of integrated management. At present the fields of
academia and engineering had been achieved some re-
sults on this issue.
On the basis of fuzzy theory, a fuzzy integrative
evaluation model of engineering management perform-
ance evaluation is developed [1,2]. Besides, main object
method [3] is used for project management performance
evaluation. However, the relationship between index sys-
tems of project management performance evaluation are
non-linear, it is difficult to determine the model to ex-
press. And the subjectivity of the evaluation process is
increased when specialists are required to determine the
index weight. So there are some drawbacks in the tradi-
tional evaluation model.
Wavelet neural network (WNN) is constrictive and
fluctuant of wavelet transform and has self-study, self-
adjustment and nonlinear mapping functions of neural
network which has made certain research achievements in
the field of pattern recognition [4].Project management
performance evaluation also belongs to pattern recognition,
thus this paper tried to set a model using wavelet neural
network model, with a view to produce good results.
2. Establishment of Index Systems in Engi-
neering Project Management Perform-
ance Evaluation
According to the main object method, which means
choosing one or two main objectives as the main objec-
tive of evaluation as long as other secondary objectives
meet certain requirements. Therefore, take project in-
vestment, construction period, quality and safety as
evaluation indexes as a basis for performance evaluation
in the project management.
According to the existing documents, the following
evaluation criteria are taken, as shown in Table 1.
3. Engineering Project Management Perform-
ance Evaluation Model Based on WNN
3.1 Structure Design of WNN Model
WNN [5] is a new type of function connected neural net-
work based on the wavelet analysis. It is beneficial for
the nonlinear function approximation, using non-linear
wavelet replace the usual nonlinear neural activation
function (such as Sigmoid function).
It is definition of the square accumulated function space:
})(:)({)(
2
2
∫
∞<= dttxtxRL
R
(1)
In the function space, select a mother wavelet function
(also known as wavelet basis function) )(x ψ to meet the
restrictive conditions:

QINGHUA ZHANG, QIANG FU 11
JSSM
∫
∞<= ω
ω
ωψ
φ
dC
R
2
)(
(2)
where: )( ωψ is the Fourier Transform of )(x ψ , then
stretch and translational transform )(x ψ , wavelet basis
function can be obtained.





−
=a
bx
a
x
ba
ψψ
1
)(
,
Rba ∈, (3)
where: a is scaling factor and b is time translation factor.
The signal can be approximated with a special con-
structed neural network. The transfer function is not
Sigmoid nonlinear function but wavelet function. This
paper uses Morlet wavelet function:
)2/exp()75.1cos()(
2
xxx −= ψ (4)
A three-layer (one input layer, one hidden layer and
one output layer) feed-forward network can approximate
a nonlinear mapping with any degree of accuracy under
normal circumstances. Aiming at the selected indexes
of project management performance evaluation, the
model will be expected to take construction period ad-
vance rates, cost saving rate, quality control scores, and
security control as the input of a network, that means
the number of input nodes is 4; take performance
evaluation value as the output, that means the number
of network output nodes is 1; the number of hidden
nodes is 10 by texting, then a 4-10-1 three-layer net-
work is established. Performance evaluation model
structure of engineering project management based on
WNN is shown in Figure 1.
3.2 Learning and Training of WNN
Through the study of network optimization indexes, set
amendment of the network and wavelet function parame-
ters by error back propagation algorithm, then reach the
most optimal learning effects gradually. Learning algo-
rithm steps as followed with application of Matlab7.0
programming:
Step 1: Set the input and output samples [6]. Produce
evenly and randomly five numbers and their relative
grades of experience given in the interval-level of Table 1
as the learning samples of network. Take 1, 2, 3, and 4 re-
spectively as the four grades of excellent, good, qualified
and poor in output layer. The data is shown in Table 2.
In order to solve the incommensurability between pro-
ject investment, construction period, quality and secu-
rity, in accordance with the project management per-
formance evaluation and the actual situation of indexes,
transform the original data of evaluation indexes into a
range of [-1,1] as input of the network using nonlinear
transformation function. Define the individual indexes
utility function [7]:
ky
ky
i
e
e
−
−
+
−
=1
1
β (5)
where: y is the relative value indicators of the actual
value and the plan value; k is relative to the impact laws
of the evaluation indexes on project management per-
formance, and it can be the experience value.
Step 2: Initialization setting. The weights, threshold
value of the network, as well as wavelet translation pa-
rameters and the scaling parameters are given evenly and
randomly in the range [-1,1].
Table 1. Level partition of quantitative indexes
Level Construction period advance rate Cost saving rate Quality control scores Security control
Excellent ≥0.12 ≥0.06 85 ≤1‰
Good 0.06≤x＜0.12 0.03≤x＜0.06 75≤x＜85 1‰≤x＜2‰
Qualified 0≤x＜0.06 0≤x＜0.03 65≤x＜75 2‰≤x＜3‰
Poor ＜0 ＜0 ＜65 ≥3‰
Construction pe-
riod advance rate
Cost saving rate
Quality control
score
Security control
Value of perfor-
mance appraisal
Input layerHidden layerOutput layer
W jk
y
X m
1
ψ
1
X m
2
X m
3
X m
4
ψ
j
ψ
n
W ij
m
Figure 1. Engineering project management performance evaluation model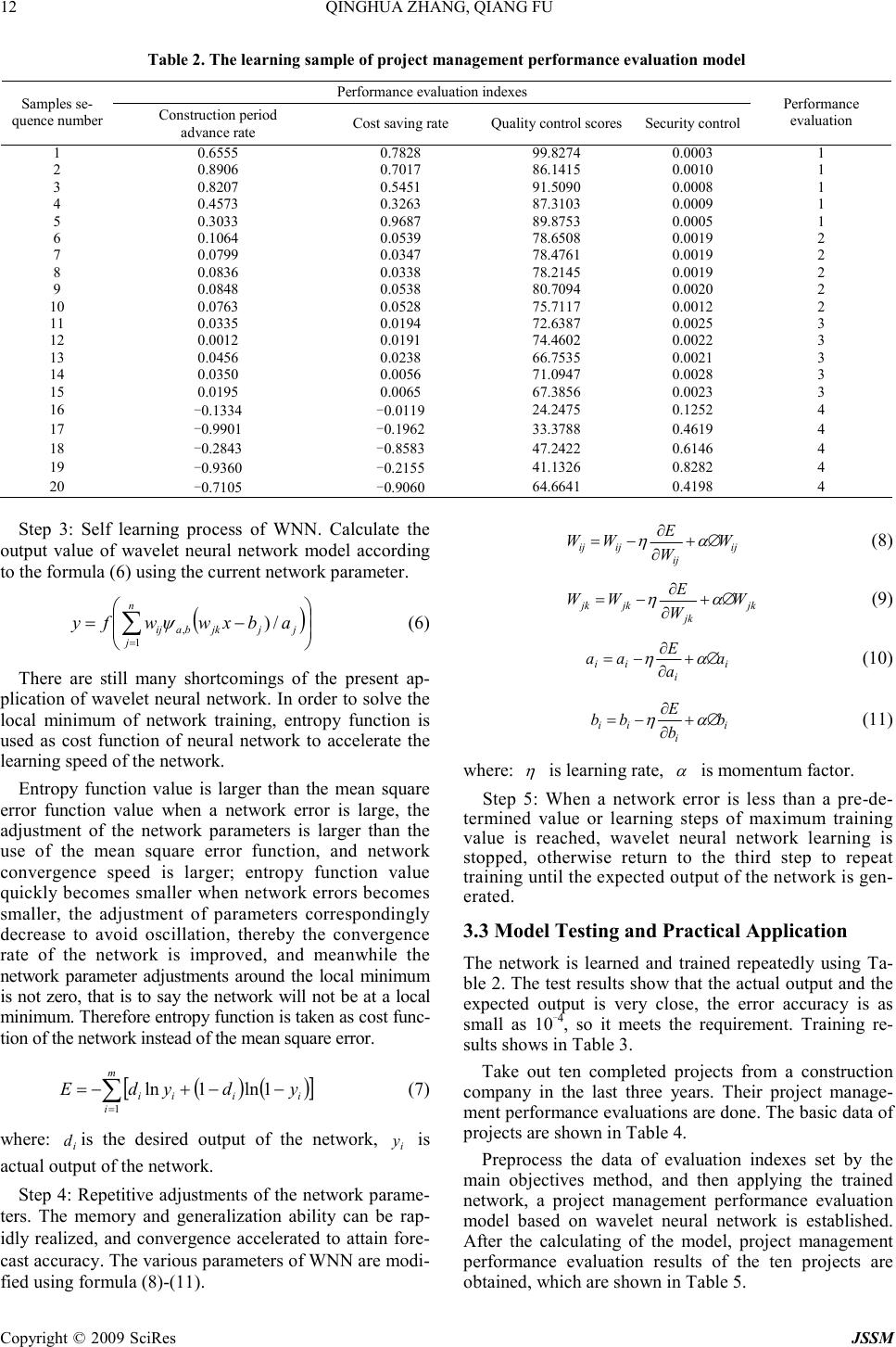

12 QINGHUA ZHANG, QIANG FU
JSSM
Table 2. The learning sample of project management performance evaluation model
Performance evaluation indexes
Samples se-
quence number
Construction period
advance rate Cost saving rate Quality control scores
Security control
Performance
evaluation
1 0.6555 0.7828 99.8274 0.0003 1
2 0.8906 0.7017 86.1415 0.0010 1
3 0.8207 0.5451 91.5090 0.0008 1
4 0.4573 0.3263 87.3103 0.0009 1
5 0.3033 0.9687 89.8753 0.0005 1
6 0.1064 0.0539 78.6508 0.0019 2
7 0.0799 0.0347 78.4761 0.0019 2
8 0.0836 0.0338 78.2145 0.0019 2
9 0.0848 0.0538 80.7094 0.0020 2
10 0.0763 0.0528 75.7117 0.0012 2
11 0.0335 0.0194 72.6387 0.0025 3
12 0.0012 0.0191 74.4602 0.0022 3
13 0.0456 0.0238 66.7535 0.0021 3
14 0.0350 0.0056 71.0947 0.0028 3
15 0.0195 0.0065 67.3856 0.0023 3
16 -0.1334 -0.0119 24.2475 0.1252 4
17 -0.9901 -0.1962 33.3788 0.4619 4
18 -0.2843 -0.8583 47.2422 0.6146 4
19 -0.9360 -0.2155 41.1326 0.8282 4
20 -0.7105 -0.9060 64.6641 0.4198 4
Step 3: Self learning process of WNN. Calculate the
output value of wavelet neural network model according
to the formula (6) using the current network parameter.
( )







−=
∑
=
n
jjjjkbaij
abxwwfy
1,
/) ψ (6)
There are still many shortcomings of the present ap-
plication of wavelet neural network. In order to solve the
local minimum of network training, entropy function is
used as cost function of neural network to accelerate the
learning speed of the network.
Entropy function value is larger than the mean square
error function value when a network error is large, the
adjustment of the network parameters is larger than the
use of the mean square error function, and network
convergence speed is larger; entropy function value
quickly becomes smaller when network errors becomes
smaller, the adjustment of parameters correspondingly
decrease to avoid oscillation, thereby the convergence
rate of the network is improved, and meanwhile the
network parameter adjustments around the local minimum
is not zero, that is to say the network will not be at a local
minimum. Therefore entropy function is taken as cost func-
tion of the network instead of the mean square error.
( )( ) [ ]
∑
=
−−+−=
m
iiiii
ydydE
1
1ln1ln (7)
where:
i
d is the desired output of the network,
i
y is
actual output of the network.
Step 4: Repetitive adjustments of the network parame-
ters. The memory and generalization ability can be rap-
idly realized, and convergence accelerated to attain fore-
cast accuracy. The various parameters of WNN are modi-
fied using formula (8)-(11).
ij
ij
ijij
W
W
E
WW∆+
∂
∂
−= αη (8)
jk
jk
jkjk
W
W
E
WW ∆+
∂
∂
−= αη (9)
i
i
ii
a
a
E
aa ∆+
∂
∂
−= αη (10)
i
i
ii
b
b
E
bb ∆+
∂
∂
−= αη (11)
where:
η
is learning rate,
α
is momentum factor.
Step 5: When a network error is less than a pre-de-
termined value or learning steps of maximum training
value is reached, wavelet neural network learning is
stopped, otherwise return to the third step to repeat
training until the expected output of the network is gen-
erated.
3.3 Model Testing and Practical Application
The network is learned and trained repeatedly using Ta-
ble 2. The test results show that the actual output and the
expected output is very close, the error accuracy is as
small as 10
- 4
, so it meets the requirement. Training re-
sults shows in Table 3.
Take out ten completed projects from a construction
company in the last three years. Their project manage-
ment performance evaluations are done. The basic data of
projects are shown in Table 4.
Preprocess the data of evaluation indexes set by the
main objectives method, and then applying the trained
network, a project management performance evaluation
model based on wavelet neural network is established.
After the calculating of the model, project management
performance evaluation results of the ten projects are
obtained, which are shown in Table 5.

QINGHUA ZHANG, QIANG FU 13
JSSM
Table 3.The comparison between desired output of the network and actual output of the network of the learning samples
Sample number 1 2 3 4 5 6 7 8 9 10
Desired output 1 1 1 1 1 2 2 2 2 2
Actual output 0.9994 1.0004 1.0007 1.0001 0.9905 2.0074 1.9893 2.0424 1.9893 1.9980
Sample number 11 12 13 14 15 16 17 18 19 20
Desired output 3 3 3 3 3 4 4 4 4 4
Actual output 2.9858 2.9844 3.0324 2.9064 3.0705 3.9992 4.0000 3.9973 4.0005 3.9989
Table 4. Basic data of projects
Schedule control/day Cost control/million yuan Quality control score Security/‰
Project
number Construction area/m
2
Plan time
Actual time Contract price Settlement price Plan Fact Plan Fact
1 109480 430 426 42632.00 42590.98 80 77 3 2
2 38962 485 487 5706.71 5610.00 80 80 3 2
3 212156 460 455 14808.53 14800.00 80 81 3 2
4 56766 365 334 9082.57 9078.13 90 85 3 0
5 130792 730 700 35655.12 35650.80 90 90 3 0
6 59004 550 548 21880.00 21850.56 87 87 3 0
7 72055 800 791 18542.00 18510.00 80 77 3 3
8 47797 355 335 7920.00 7856.00 75 69 3 1
9 98000 360 335 12000.00 11890.67 75 65 3 2
10 90009 560 547 1112.80 1112.02 75 72 3 1
Table 5. Results of performance evaluation
Project number 1 2 3 4 5 6 7 8 9 10
Output of network 2.9685 3.1004 2.9372 1.0166 2.1092 2.9166 3.1209 2.0630 2.9191 3.0247
Evaluate result 3 3 3 1 2 3 3 2 3 3
Seen from Table 5, all these ten projects have reached
more than qualified rating. One of them is excellent and
two of them are good. Evaluation results can be used as
the basis of the plan implementation of future projects,
progress control, cost assessment, quality control and
security control, and it is helpful to enhance the level of
integrated management.
4. Conclusions
Started from the purpose and requirements of project
management performance evaluation, using the charac-
teristics of wavelet neural networks which can describe
the complex and nonlinear relationship, the relationship
model between evaluation indexes and project manage-
ment performance evaluation is established. The followed
three conclusions are obtained:
1) There is no need to determine the weights by peo-
ple using wavelet neural network model in the evalua-
tion process, so the defects brought by experts when de-
termining the weight is eliminated, therefore the accuracy
and objectivity of the evaluation result is improved.
2) In order to avoid wavelet neural network training
being at a local minimum, entropy function is taken as
cost function of the network instead of the mean square
error to accelerate the learning speed of the network .The
testing proves the method feasible.
3) Performance evaluation model based on wavelet
neural network explores a new way for project manage-
ment performance evaluation, and enriches the perform-
ance evaluation method. The model has strong feasibility
and accuracy which can be used as a scientific and ra-
tional basis for performance evaluation.
Table 5. Results of performance evaluation
Project number 1 2 3 4 5 6 7 8 9 10
Output of network 2.9685 3.1004 2.9372 1.0166 2.1092 2.9166 3.1209 2.0630 2.9191 3.0247
Evaluate result 3 3 3 1 2 3 3 2 3 3

14 QINGHUA ZHANG, QIANG FU
JSSM
REFERENCES
[1] L. X. Zhang, “Fuzzy comprehensive evaluation of the
expressway project management performance evalua-
tion,” Road traffic technology (applications) 5, pp. 169 - 171,
2007.
[2] S. H. Cai, M. Y. Zhou, and Z. C. Ye, “Fuzzy integrative
evaluation method of management performance of engi-
neering project,” Journal of YangZhou university (natural
science), 5, pp. 57 - 60, 2002.
[3] V. Ireland, “The role of management actions in the cost,
time and quality performance of high-rise commer
cial building projects,” Construction Management and
Economics, 3, pp. 59 - 87, 1985.
[4] T. Brian and H. Szu, “Adaptive wavelet classification of
acoustic backscatter and imagery,” Optical Engineering, 7,
pp. 2192 - 2202, 1994.
[5] Q. H. Zhang and A. Benveniste, “Wavelet networks,”
IEEE Transactions on Neural Networds, 6, 889 - 898,
1992.
[6] X. Y. Zhao., Q. Fu, and Z. X. Xing, “Application of pro-
jection pursuit grade evaluation model in comprehensive
evaluation of changes in soil quality,” Acta Pedologica
Sinica. 1, pp. 164 - 168, 2007.
(Edited by Vivian and Ann)