Communications and Network, 2010, 2, 162-165
doi:10.4236/cn.2010.23024 Published Online August 2010 (http://www.SciRP.org/journal/cn)
A Novel Black Box Based Behavioral Model of Power
Amplifier for WCDMA Applications
Amandeep Singh Sappal, Manjeet Singh Patterh, Sanjay Sharma2
1University College of Engineering, Punjabi University Patiala, Punjab, India,
2Dept. of ECE, Thapar University, Punjab, India
Received June 28, 2010; revised August 10, 2010; accepted August 15, 2010
Abstract
In this paper, Black Box approach is presented for behavioral modeling of a non linear power amplifier with
memory effects. Large signal parameters of a Motorola LDMOS power amplifier driven by a WCDMA signal
were extracted while taking into considerations the power amplifier’s bandwidth. The proposed model was
validated based on the simulated data. Some validation results are presented both in the time and frequency
domains, using WCDMA signal.
Keywords: Behavioral Model, Black Box, Power Amplifiers
1. Introduction
The introduction of the third generation UMTS, based on
WCDMA technology, is a further step towards satisfying
the ever increasing demand for data/internet services. 3G
is quickly moving on to 3.5G, 3.9G, and 4G and is
changing the way the world communicates. The evolu-
tion of wireless technologies including CDMA2000,
GPRS, EGPRS, WCDMA, HSDPA and 1xEV, allow
development of new wireless devices that combine voice,
internet, and multimedia services. In the future GSM and
other parallel 2G systems are likely to be replaced with
3G and beyond, and the bands that today are used for
GSM will then be used for WCDMA and other standards.
WCDMA in the 900 MHz band is a cost effective way to
deliver nationwide high-speed wireless coverage .This
evolution has brought new requirements on the RF parts
of the transceivers, especially the Power Amplifier (PA).
Thus the simulation of PA circuits is becoming a very
important issue in nowadays communication scenarios.
Due to broadband nature of signals, frequency-depen-
dent behavior of PA is encountered, i.e ., memory effects.
To accurately model a PA, we have to take into account
both nonlinearities and memory effects. Several works
have recently been published proposing behavioral models
and extraction procedures for envelope behavioral model
simulation [1-4]. The Volterra series has been used by
several researchers to describe the relationship between
the input and the output of a power amplifier with
memory effects [1]. However, high computational com-
plexity makes methods of this kind impractical in some
real cases, e.g., modeling a PA with strong nonlinearities
and/or with long-term memory effects. This is because
the number of coefficients to be estimated in the model
increases exponentially with the degree of nonlinearity
and with the memory length of the system. To overcome
the modeling complexity, various model-order reduction
approaches have been proposed to simplify the Volterra
model structure [5-15]. Although these simplified models
have been employed to characterize PAs with reasonable
accuracy under certain conditions, there is no systematic
way to verify if the model structure chosen is truly
appropriate to the PA under study. In this paper the
principle of a novel approach, called ‘Black Box’ has
been presented. The Black Box model is directly derived
from the topology of the amplifier.
The variables used to describe the signals at both ports
are the classical incident and scattered voltage waves
[16], typically defined in a characteristic impedance of
50 Ω, together with the dc current and voltage biasing
parameters.
Input Signal
Figure 1. Parameter estimation of Black Box model
parameters.
Device under Test
(DUT)
Bias
Voltages
Parameter
Extraction

A. S. SAPPAL ET AL.163
2. Description of Black Box Model
The Black Box model is derived directly from the circuit
topology of the PA. The transistors can be considered to
be two port non-linear networks which can be modeled
in terms of nonlinear scattering parameters. If
1,2 and 1,2 represents the incident and
reflected waves respectively. Using first order Taylor
series expansion, the scattering parameter model of PA
can be written as [16]

ij
caa bb
 
  
12
22
*
11 11211
11
1
*
22
2 21 12211
0
0
Sa SaSa
ba
a
ba
a
Sa SaSa




 
 

 

 





(1)

ij i
Sa
   








12
22
1
2
1111112 1 121
2
21121221 22
*
112 1
*
2 122
..
..
0.
0
b
b
Sac Saca
a
SacSac
Sac a
a
Sac























(2)


ij
c

represents the normalized frequency function.
3. Valediction of the Proposed Model
The proposed model is implemented in Agilent ADS at a
frequency of 1950 MHz. The input signal power is
varied from 0 to 20 dB. The model is implemented for
Motorola LDMOS PA circuit available in Agilent library
as shown in Figure 2 and the measurement setup is
shown in Figure 3. The data file has been extracted for

represents non-linear scattering parameters as a
function of input waves. But in real practice scattering pa-
rameters are also found to be function of PA band width.
So in order to consider the effect of PA bandwidth also
(1) is modified as [17]
Figure 2. Motorola PA circuit topology used to validate the proposed model.
CIRCUIT BIAS SETUP
Motorola_PA
X2
Ldrainline2=1161 mil
Ldrainline1=540 mil
Lgateline2=610 mil
Lgateline1=1425 mil
AmplifierS2D_Setup
X1
SSFreq_Step=-1.0 Hz
SSFreq_Stop=-1.0 Hz
SSFreq_Start=-1.0 Hz
Pin_Step=2 _dB
Pin_Stop=20 _dBm
Pin_Start=0 _dBm
Freq_Step=0.1 GHz
Freq_Stop=1950 MHz
Freq_Start=1950 MHz
Order=11
Filename="Motorola_PA.s2d"
S2D
Setup
Agilent Technologies
outin
ParamSweep
Sweep_BiasL
Step=0.1
Stop=2.1
Start=1.9
SimInstanceName[6]=
SimInstanceName[5]=
SimInstanceName[4]=
SimInstanceName[3]=
SimInstanceName[2]=
SimInstanceName[1]="Sweep_BiasU"
SweepVar="BiasL"
PARAMETER SWEEP
ParamSweep
Sweep_BiasU
Step=0.5
Stop=6.3
Start=5.3
SimInstanceName[6]=
SimInstanceName[5]=
SimInstanceName[4]=
SimInstanceName[3]=
SimInstanceName[2]=
SimInstanceName[1]="X1.HB1"
SweepVar="BiasU"
PARAMETER SWEEP
V_DC
SRC4
Vdc=Bias L
V_DC
SRC3
Vdc=Bias U
VAR
VAR1
Bi asL=2.0
Bi asU=5.8
Eqn
Var
Figure 3. The setup for measurement of parameters.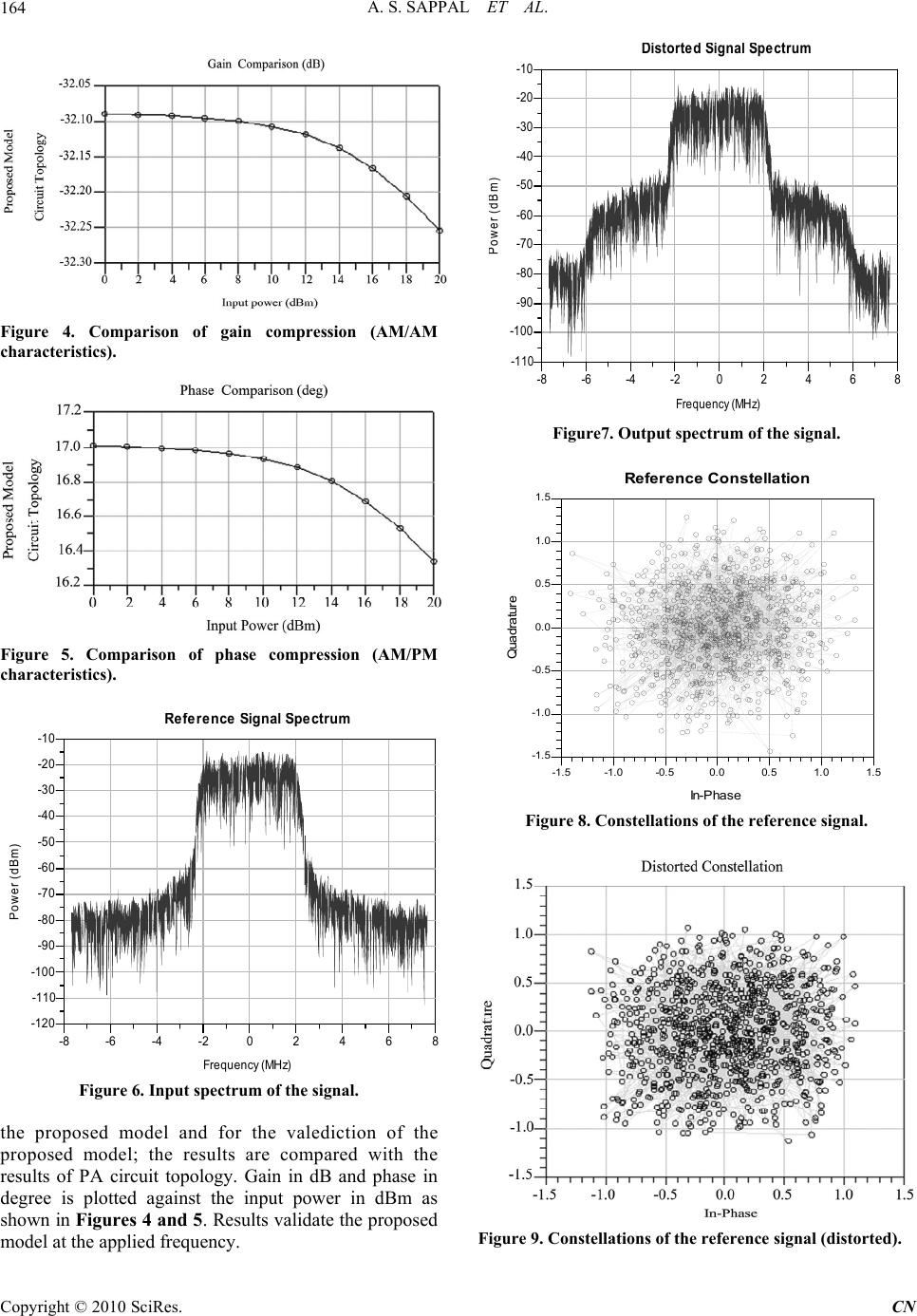

A. S. SAPPAL ET AL. 164
Figure 4. Comparison of gain compression (AM/AM
characteristics).
Figure 5. Comparison of phase compression (AM/PM
characteristics).
-6-4-20 2 4 6-88
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-120
-10
Frequency (MHz)
P
ower
(dB
m
)
R
e
f
erence
Si
gna
l
S
pectrum
Figure 6. Input spectrum of the signal.
the proposed model and for the valediction of the
proposed model; the results are compared with the
results of PA circuit topology. Gain in dB and phase in
degree is plotted against the input power in dBm as
shown in Figures 4 and 5. Results validate the proposed
model at the applied frequency.
-6-4-20246-8 8
-100
-90
-80
-70
-60
-50
-40
-30
-20
-110
-10
Frequency (MHz)
P
ower
(dB
m
)
Di
storte
d
Si
gna
l
S
pectrum
Figure7. Output spectrum of the signal.
-1.0-0.50.0 0.5 1.0-1.5 1.5
-1. 0
-0. 5
0.0
0.5
1.0
-1. 5
1.5
In-Phas e
Quadrature
Reference Constellation
Figure 8. Constellations of the reference signal.
Figure 9. Constellations of the reference signal (distorted).
C
opyright © 2010 SciRes. CN

A. S. SAPPAL ET AL. 165
4. Measurement of Parameters on A
WCDMA Signal
The proposed model was also tested for measurements
on a WCDMA signal centered on 1950 MHz. Input and
output spectrum of the input signal and the output signal
were measured.
Upper channel Adjacent Channel Leakage Ratio
(ACLR) for the reference signal is -52.476 and for the
distorted signal is -34.525. Also Lower channel Adjacent
Channel Leakage Ratio (ACLR) for the reference signal
is -52.717 and for the distorted signal is -34.608. Con-
stellations of the reference signal and the distorted signal
are also plotted as show in Figures 8 an d 9 respectively.
The peak value of Error vector magnitude (EVM) of
the reference signal was calculated as 35.13% and
53.21% respectively.
5. Conclusions
A novel behavioral model based on a Black Box
modeling is presented. The model has been validated
using Motorola LDMOS power amplifier. The results
have been validated both in time and in frequency
domain. This new enables a good prediction of the PA’s
behavior. Some measurements of important parameters
(like ACLR and EVM) used to describe the nonlinear
behavior of the power amplifier driven by WCDMA
signal has been also carried out.
6. References
[1] A, Zhu and T. J. Brazil, “Behavioral Modeling of RF
Power Amplifiers Based on Pruned Volterra Series,”
IEEE Microwave and Wireless Components Letters, Vol.
14, No. 12, December 2004, pp. 563- 565.
[2] N. Le Galou, E. Ngoya, H. Buret, D. Barataud and J.M.
Nebus, “An Improved Behavioral Modeling Technique
for High Power Amplifiers with Memory,” IEEE MTT-S
International Microwave Symposium, Vol. 2, May 2001,
pp. 983-986.
[3] T. Wang and T. J. Brazil, “Volterra-Mapping-Based Be-
havioral Modeling of Nonlinear Circuits and Systems for
High Frequencies,” IEEE Transactions on Microwave
Theory and Technology, Vol. MTT-51, May 2003, pp.
1433-1440.
[4] M. Ibnkahla, N. J. Bershad, J. Sombrin and F. Castanié,
“Neural Network Modeling and Identification of Nonlinear
Channels with Memory: Algorithms, Applications, and
Analytic Models,” IEEE Transactions on Signal Processing,
Vol. SP- 46, May 1998, pp.1208-1220.
[5] J. C. Pedro and S. A. Maas, “A comparative Overview of
Microwave and Wireless Power-amplifier Behavioral
Modeling Approaches,” IEEE Transactions on Micro-
wave Theory Technology, Vol. 53, No. 4, April 2005, pp.
1150-1163.
[6] H. Ku, M. Mckinley and J. S. Kenney, “Quantifying
Memory Effects in RF Power Amplifiers,” IEEE Trans-
actions on Microwave Theory Technology, Vol. 50, No.
12, December 2002, pp. 2843-2849.
[7] J. Kim and K. Konstantinou, “Digital Predistortion of
Wideband Signals Based on Power Amplifier Model with
Memory,” Electronics Letters, Vol. 37, No. 23, Novem-
ber 2001, pp. 1417-1418.
[8] A. Zhu and T. J. Brazil, “Behavioral Modeling of RF
Power Amplifiers Based on Pruned Volterra Series,”
IEEE Microwave and Wireless Components Letter, Vol.
14, December 2004, pp. 563-565.
[9] C. Silva, A. Moulthrop, and M. Muha, “Introduction to
Poly-spectral Modeling and Compensation Techniques
for Wideband Communications Systems,” 58th ARFTG
Conference Digest, San Diego, November 2001, pp. 1-15.
[10] D. Mirri et al., “A nonlinear Dynamic Model for Per-
formance Analysis of Large-signal Amplifiers in Com-
munication Systems,” IEEE Transactions on Instrumen-
tation Measurement, Vol. 53, No. 2, April 2004. pp.
341-350.
[11] E. Ngoya et al., “Accurate RF and Microwave System
Level Modeling of Wideband Nonlinear Circuits,” IEEE
MTT-S International Microwave Symposium Digest, Bos-
ton, Vol. 1, June 2000, pp. 79-82.
[12] A. Zhu, J. Dooley and T. J. Brazil, “Simplified Volterra
Series Based Behavioral Modeling of RF Power Amplifi-
ers Using Deviation Reduction,” IEEE MTT-S Interna-
tional Microwave Symposium Digest, San Francisco, 2006,
pp. 1113-1116.
[13] A. Zhu, J. C. Pedro and T. J. Brazil, “Dynamic Deviation
Reduction Based Volterra Behavioral Modeling of RF
Power Amplifiers,” IEEE Transaction on Microwave
Theory Technology, Vol. 54, No. 12, December 2006, pp.
4323-4332.
[14] A. Zhu and T. J. Brazil, “RF Power Amplifiers Behav-
ioral Modeling Using Volterra Expansion with Laguerre
Functions,” IEEE MTT-S International Microwave Sym-
posium Digest, 2005, pp. 963-966.
[15] M. Isaksson and D. Rönnow, “A Kautz–Volterra Behav-
ioral Model for RF Power Amplifiers,” IEEE MTT-S In-
ternational Microwave Symposium Digest, 2006, pp.
485-488.
[16] Verspecht, J, “Scattering Functions for Nonlinear Behav-
ioral Modeling in the Frequency Domain,” “Fundamen-
tals of Nonlinear Behavioral Modeling: Foundations and
Applications Workshop,” IEEE MTT-S International Mi-
crowave Symposium, June 2003, pp. 1-26.
[17] F. X. Estagerie, T. Reveyrand, S. Mons, R. Quéré, L.
Constancias and P. Le Helleye, “From Circuit Topology
to Behavioral Model of Power Amplifier Dedicated to
Radar Applications,” Electronics Letters , Vol. 43, No. 8,
April 2007, pp. 477-479.