Engineering, 2010, 2, 625-634
doi:10.4236/eng.2010.28080 Published Online August 2010 (http://www.SciRP.org/journal/eng).
Lie Group Analysis for the Effects of Variable Fluid
Viscosity and Thermal Radiation on Free Convective Heat
and Mass Transfer with Variable Stream Condition
P. Loganathan1, P. Puvi Arasu2
1Department of Mathematics, Anna University, Chennai, India
2Erode Sengunthar Engineering College, Thudupathi, India
Received December 23, 2009; revised February 26, 2010; accepted March 6, 2010
Abstract
Natural convective boundary layer flow and heat and mass transfer of a fluid with variable viscosity and
thermal radiation over a vertical stretching surface in the presence of suction/injection is investigated by Lie
group analysis. Fluid viscosity is assumed to vary as a linear function of temperature. The symmetry groups
admitted by the corresponding boundary value problem are obtained by using a special form of Lie group
transformations viz. scaling group of transformations. An exact solution is obtained for translation symmetry
and numerical solutions for scaling symmetry. The effects of fluid viscosity and thermal radiation on the di-
mensionless velocity, temperature and concentration profiles are shown graphically. Comparisons with pre-
viously published works are performed and excellent agreement between the results is obtained. The conclu-
sion is drawn that the flow field and temperature profiles are significantly influenced by these parameters.
Keywords: Scaling Group of Transformations, Free Convective Flow, Temperature-Dependent Fluid
Viscosity, Suction/Blowing, Thermal Radiation
1. Introduction
The study of natural convection flow for an incompressi-
ble viscous fluid past a heated surface has attracted the
interest of many researchers in view of its important ap-
plications to many engineering problems such as cooling
of nuclear reactors, the boundary layer control in aero-
dynamics, crystal growth, food processing and cooling
towers. In this paper, symmetry methods are applied to a
natural convection boundary layer problem. The main
advantage of such methods is that they can successfully
be applied to non-linear differential equations. The sym-
metries of differential equations are those continuous
groups of transformations under which the differential
equations remain invariant, that is, a symmetry group
maps any solution to another solution. The symmetry
solutions are quite popular because they result in the re-
duction of the number of independent variables of the
problem.
A class of flow problems with obvious relevance to
polymer extrusion is the flow induced by the stretching
motion of a flat elastic sheet. In a melt-spinning process,
the extrudate from the die is generally drawn and simul-
taneously stretched into a filament or sheet, which is
thereafter solidified through rapid quenching or gradual
cooling by direct contact with water or chilled metal rolls.
In fact, stretching imports a unidirectional orientation to
the extrudate, thereby improving its mechanical proper-
ties and the quality of the final product greatly depends
on the rate of cooling. Crane [1] was the first who stud-
ied the motion set up in the ambient fluid due to a line-
arly stretching surface. Several authors see e.g., the ref-
erences cited in [2], have subsequently explored various
aspects of the accompanying heat transfer occurring in
the infinite fluid medium surrounding the stretching
sheet. The hydrodynamics of a finite fluid medium, i.e. a
thin liquid film, on a stretching sheet was first considered
by Wang [3] who by means of a similarity transforma-
tion reduced the unsteady Navier–Stokes equations to a
non-linear ordinary differential equation. The accompa-
nying heat transfer problem was solved more recently by
Andersson et al. [2]. In these studies the film surface was
planar and free of any stresses.
The production of sheeting material arises in a number
of industrial manufacturing processes and includes both
metal and polymer sheets. It is well known that the flow

P. LOGANATHAN ET AL. 626
in a boundary layer separates in the regions of adverse
pressure gradient and the occurrence of separation has
several undesirable effects in so far as it leads to increase
in the drag on the body immersed in the flow and ad-
versely affects the heat transfer from the surface of the
body. Several methods have been developed for the pur-
pose of artificial control of flow separation. Separation
can be prevented by suction as the low-energy fluid in
the boundary layer is removed [4,5]. On the contrary, the
wall shear stress and hence the friction drag is reduced
by blowing. Free convective phenomenon has been the
object of extensive research. The importance of this
phenomenon is increasing day by day due to the en-
hanced concern in science and technology about buoy-
ancy induced motions in the atmosphere, the bodies in
water and quasisolid bodies such as earth. Natural con-
vection flows driven by temperature differences are very
much interesting in case of Industrial applications. Buoy-
ancy plays an important role where the temperature dif-
ferences between land and air give rise to a complicated
flow and in enclosures such as ventilated and heated
rooms (Elbashbeshy and Bazid [6]).
So such type of problem, which we are dealing with, is
very much useful to polymer technology and metallurgy.
Cheng and Minkowycz [7] and Cheng [8] studied the
free convective flow in a saturated porous medium.
Wilks [9] had studied the combined forced and free con-
vection flow along a semi-infinite plate extending verti-
cally upwards with its leading edge horizontal. Boutros
et al. [10] solved the steady free convective boundary
layer flow on a nonisothermal vertical plate. Recently,
any studies were made on the steady free convective
boundary layer flow on moving vertical plates consider-
ing the effect of buoyancy forces on the boundary layer
Chen and Strobel [11], Ramachandran et al. [12], Lee
and Tsai [13]. The radiative effects have important ap-
plications in physics and engineering particularly in
space technology and high temperature processes. But
very little is known about the effects of radiation on the
boundary layer. Thermal radiation effects may play an
important role in controlling heat transfer in polymer
processing industry where the quality of the final product
depends on the heat controlling factors to some extent.
High temperature plasmas, cooling of nuclear reactors,
liquid metal fluids, power generation systems are some
important applications of radiative heat transfer from a
vertical wall to conductive gray fluids. The effect of ra-
diation on heat transfer problems have studied by Hos-
sain and Takhar [14], Takhar et al. [15], Hossain et al.
[16]. In all of the above mentioned studies, fluid viscos-
ity was assumed to be constant. However, it is known
that the physical properties of fluid may change signifi-
cantly with temperature. For lubricating fluids, heat gen-
erated by the internal friction and the corresponding rise
in temperature affects the viscosity of the fluid and so the
fluid viscosity can no longer be assumed constant. The
increase of temperature leads to a local increase in the
transport phenomena by reducing the viscosity across the
momentum boundary layer and so the heat transfer rate
at the wall is also affected. Therefore, to predict the flow
behaviour accurately it is necessary to take into account
the viscosity variation for incompressible fluids. Gary et
al. [17] and Mehta and Sood [18] showed that, when this
effect is included the flow characteristics may changed
substantially compared to the constant viscosity assump-
tion. Mukhopadhyay et al. [19] investigated the MHD
boundary layer flow with variable fluid viscosity over a
heated stretching sheet. Recently, Mukhopadhyay and
Layek [20] studied the effects of thermal radiation and
variable fluid viscosity on free convective flow and heat
transfer past a porous stretching surface.
Many authors have constructed an exponential type of
exact solution using the translation symmetry and a se-
ries type of approximate solution using the scaling sym-
metry and also discussed some boundary value problems.
So far no attempt has been made to study the heat and
mass transfer in a vertical stretching surface using Lie
groups and hence we study the problem of natural con-
vection heat and mass transfer flow past a stretching
sheet for various parameters using Lie group analysis.
2. Mathematical Analysis
We consider a free convective, laminar boundary layer
flow and heat and mass transfer of viscous incompressi-
ble fluid over a vertical stretching sheet emerging out of
a slit at origin (x = 0, y = 0) and moving with non-uni-
form velocity U(x) in the presence of thermal radiation
(Figure 1).
The governing equations of such type of flow are, in
the usual notations,
0
uv
xy



 (1)
Figure 1. Physical model of boundary layer flow over a
vertical stretching surface.

P. LOGANATHAN ET AL. 627
2
*
2
1[( )()]
uu
uv
xy
Tuu gTTg CC
Tyyx






 
 
 
 (2)
2
2
1r
pp
q TT T
uv
x
yc cy y


  
 
   (3)
2
2
CC C
uv D
xy y
 

  (4)
(), (),,0
ww
uUxvVxCCTTaty
0, ,uCCTTasy

  (5)
when the viscous dissipation term in the energy equation
is neglected (as the fluid velocity is very low). Here u
and v are the components of velocity respectively in
the
x
and y directions,

is the coefficient of fluid
viscosity,

is the fluid density (assumed constant), T
is the temperature,
 is the thermal conductivity of the
fluid, Dis diffusional coefficient,

is the volumetric
coefficient of thermal expansion, *

is the volumetric
coefficient of concentration expansion, g is the gravity
field, T is the temperature at infinity, where ()Ux is
the stream wise velocity and ()Vx is the velocity of
suction of the fluid, w Tis the wall temperature.
Using Rosseland approximation for radiation (Brew-
ster [21]) we can write
4
1
*
4
3
r
T
qy
k
 
 where 1

is the
Stefan–Boltzman constant, k* is the absorption coeffi-
cient.
Assuming that the temperature difference within the
flow is such that 4
T may be expanded in a Taylor se-
ries and expanding 4 T about T and neglecting
higher orders we get 43 4 43TTTT



Therefore, the Equation (3) becomes
3 22
1
2*2
16
3
pp
T TT TT
uv
xyc
ycky
 


 
 
 
(6)
We now introduce the following relations for
,,uv and

 as
uy


,v
x


 ,
w
TT
TT



and
w
CC
CC




 (7)
where u is the stream function. The stream wise ve-
locity and the suction/injection velocity are taken as
1
2
0
(), ()
m
m
UxcxVxV x

 (8)
Here 0cis constant, w
T is the wall temperature,
the power-law exponent m is also constant. In this
study we take 1c.
The temperature-dependent fluid viscosity is given by
(Batchelor [22]),
*[( )]
w
abTT  
where *

is the constant value of the coefficient of
viscosity far away from the sheet and ba, are constants
and (0)b. For a viscous fluid, Ling and Dybbs [23]
suggest a viscosity dependence on temperature T of the
form [1 ()]TT




 where c is a thermal property
of the fluid and


is the viscosity away from the hot
sheet. This relation does not differ at all with our formu-
lation. The range of temperature, i.e., ()
w
TT

studied
here is0
(023 )C.
Using the relations (5) in the boundary layer Equation
(2) and in the energy and diffusion Equations (3) and (4)
we get the following equations
22
2
23
** *
23
[(1)]( )
yxy xy
vva g
yb yy
 
 


 

 
 


(9)
32
1
*2
16
()
3
pp
T
yx xycck y


 



 

  (10)
2
2
D
yx xyy

 



  (11)
where
*
*
(),
w
bTTv




 
The boundary conditions Equation (5) become
1
2
0
,,
10; 0,0,0
m
m
xVx
yx
atyas y
y


 






 

(12)
We now introduce the simplified form of Lie-group
transformations namely, the scaling group of transforma-
tions (Mukhopadhyay et al. [19]),
3 12
567 4
** *
** **
:, ,,
,, ,
xxeyyee
uuevveee
  

 

 
 

(13)
Equation (13) may be considered as a point-transfor-
mation which transforms co-ordinates (, ,,,,, )xy uv


to the coordinates ** *****
(,,,,,, )xy uv

 .
Substituting (13) in (9), (10) and (11) we get,

P. LOGANATHAN ET AL. 628
123
236
23 236
67
*2* *2*
(2 2)
**** *2
*2*
(3 ) *
**2
3* 3*
(3 )(3) ***
*3 *3
** *
[]
()
eyxyx y
ve yy
va eve
yy
ge e
b
 
 
  
 
 










 











 


(14)
1236
26
** **
()
** **
32*
(2 )
1
**2
16
3
pp
eyx xy
Te
cck y
 

 
 





 



 



 



(15)
1237
27
** **
()
** **
2*
(2 )
*2
eyx xy
De y
 

 




 



 



(16)
The system will remain invariant under the group of
transformations , we would have the following relations
among the parameters, namely
123 236 23
671236
261237 27
223 3
;
22and






 

These relations give6721 3
11
0, 43

  .
The boundary conditions yield411
1,
2
m

 
511
11 1
()
24 2
mas m


 
In view of these, the boundary conditions become
11
()
24
**
*****
0
*
*
** *
*
,,1
00,0,0
x
Vx aty
x y
andas y
y
 



 


 

(17)
The set of transformations

reduces to
3
11
44
1
11
24
** *
** **
,, ,
,,,,
xxe yyee
uuevve







 


 
Expanding by Taylor’s method in powers of

and
keeping terms up to the order

we get
** * 11
1
** **
11
3
,, ,
44
,, 0
24
xxx yyy
uuuvv v

 


 
 
In terms of differentials these yield
1111
1300
4424
dxdyddudv d d
xyuv






Solving the above equations we get,
13
44
*** ***
,(),(),()yxx F



  (18)
With the help of these relations, the (14), (15) and (16)
become
2*
** *
23 4
4()44 ()
FFF vF
avFvF g
b





 
 
 
(19)
3
1
*
16
430
3
pp
TF
cck
 



 





(20)
430DF





 (21)
The boundary conditions take the following form
0
4
1,, 1
3
00,0,0
V
FF at
and Fas
 
 
 
 
(22)
Again, we introduce the following transformations for
,,
F
and

 in Equations (19), (20) and (21):
11 11
11 11
** ** 11
*
** ** 11
1
(), (),
() ,()2
bb
bb
gg
vF vF
bb
gg
vvwhere
bb










  


 
(23)
Taking *,andFf



 the Equations
(19), (20) and (21) finally take the following form
2
4( )44
23 4()
aF F F
FFF




 





 (24)
44
130
Pr 3F N







 (25)
430F
Sc




 (26)
where
**
Pr
p
p
vcc 


is the Prandtl number,
*
3
1
4
k
NT



is the Radiation parameter,
*
v
Sc D

is the
Schmidt number. The boundary conditions take the fol-
lowing forms.
**
1, ,1,
00,0,0
ffS
atand fas







 
(27)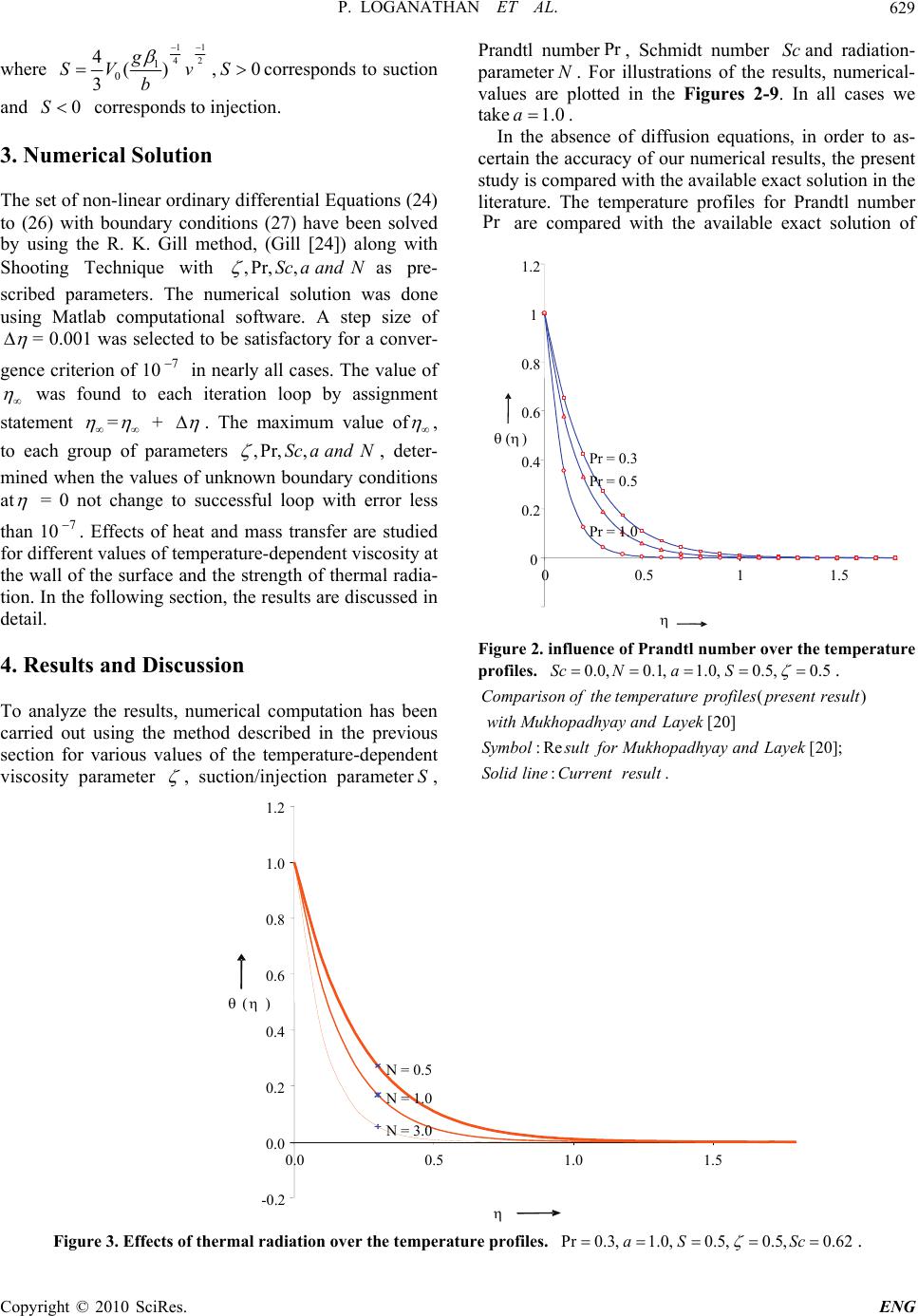

P. LOGANATHAN ET AL. 629
where
11
42
1
0
4()
3
g
SV v
b


,0Scorresponds to suction
and 0S corresponds to injection.
3. Numerical Solution
The set of non-linear ordinary differential Equations (24)
to (26) with boundary conditions (27) have been solved
by using the R. K. Gill method, (Gill [24]) along with
Shooting Technique with ,Pr, ,ScaandN

as pre-
scribed parameters. The numerical solution was done
using Matlab computational software. A step size of

= 0.001 was selected to be satisfactory for a conver-
gence criterion of 107 in nearly all cases. The value of

 was found to each iteration loop by assignment
statement

=

 +

. The maximum value of


,
to each group of parameters ,Pr, ,ScaandN

, deter-
mined when the values of unknown boundary conditions
at

= 0 not change to successful loop with error less
than 107. Effects of heat and mass transfer are studied
for different values of temperature-dependent viscosity at
the wall of the surface and the strength of thermal radia-
tion. In the following section, the results are discussed in
detail.
4. Results and Discussion
To analyze the results, numerical computation has been
carried out using the method described in the previous
section for various values of the temperature-dependent
viscosity parameter

, suction/injection parameterS,
Prandtl numberPr , Schmidt number Sc and radiation-
parameterN. For illustrations of the results, numerical-
values are plotted in the Figures 2-9. In all cases we
take 1.0a

.
In the absence of diffusion equations, in order to as-
certain the accuracy of our numerical results, the present
study is compared with the available exact solution in the
literature. The temperature profiles for Prandtl number
Pr are compared with the available exact solution of
Figure 2. influence of Prandtl number over the temperature
profiles. 0.0,0.1, 1.0,0.5,0.5Sc Na S


 .
()
[20]
: Re[20];
:.
Comparison ofthe temperatureprofilespresentresult
with Mukhopadhyay andLayek
SymbolsultforMukhopadhyay andLayek
Solid lineCurrentresult
Figure 3. Effects of thermal radiation over the temperature profiles. Pr 0.3,1.0,0.5,0.5,0.62aS Sc  .
Pr = 0.3
Pr = 0.5
Pr = 1.0
0
0.2
0.4
0.6
0.8
1
1.2
00.5 11.5


(

 )
N
= 0.5
N
= 1.0
N
= 3.0
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0.00.51.01.5

 (  )

P. LOGANATHAN ET AL. 630
Figure 4. Effects of fluid viscosity over the velocity profiles. 0.62,0.1,1.0,0.5,Pr0.71ScNa S

.
Figure 5. Effects of fluid viscosity over the temperature profiles. 0.62,0.1,1.0,0.5,Pr0.71ScNa S .
Mukhopadhyay and Layek [20], is shown in Figure 2. It
is observed that the agreements with the theoretical solu-
tion of temperature profiles are excellent. For a givenN,
it is clear that there is a fall in temperature with in-
creaseing the Prandtl number. This is due to the fact that
there would be a decrease of thermal boundary layer
thickness with the increase of Prandtl number as one can
see fromFigure 3 by comparing the curves with
Pr0.3andPr 1.0. This behavior implies that fluids
having a smaller Prandtl number are much more respon-
sive to thermal radiation than fluids having a larger
Prandtl number.
Figure 3 illustrates the typical temperature profiles for
various values of the thermal radiation parameterN. At
a particular value ofN, the temperature decreases with
accompanying decreases in the thermal boundary layer
thickness by increasing the values of Pr . Further, it is ob-
vious that for a givenPr , the temperature is decreased
with an increase inN. This result can be explained by
the fact that a decrease in the values of
*
3
1
()
4
k
NT




for given *andkT

means a decrease in the Rosseland
radiation absorptivity. According to Equations (2) and (3)

= 1.0

= 0.5

= 0.1
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5

f '( 
)

= 0.1

= 0.5
= 1.0
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
0 0.51 1.5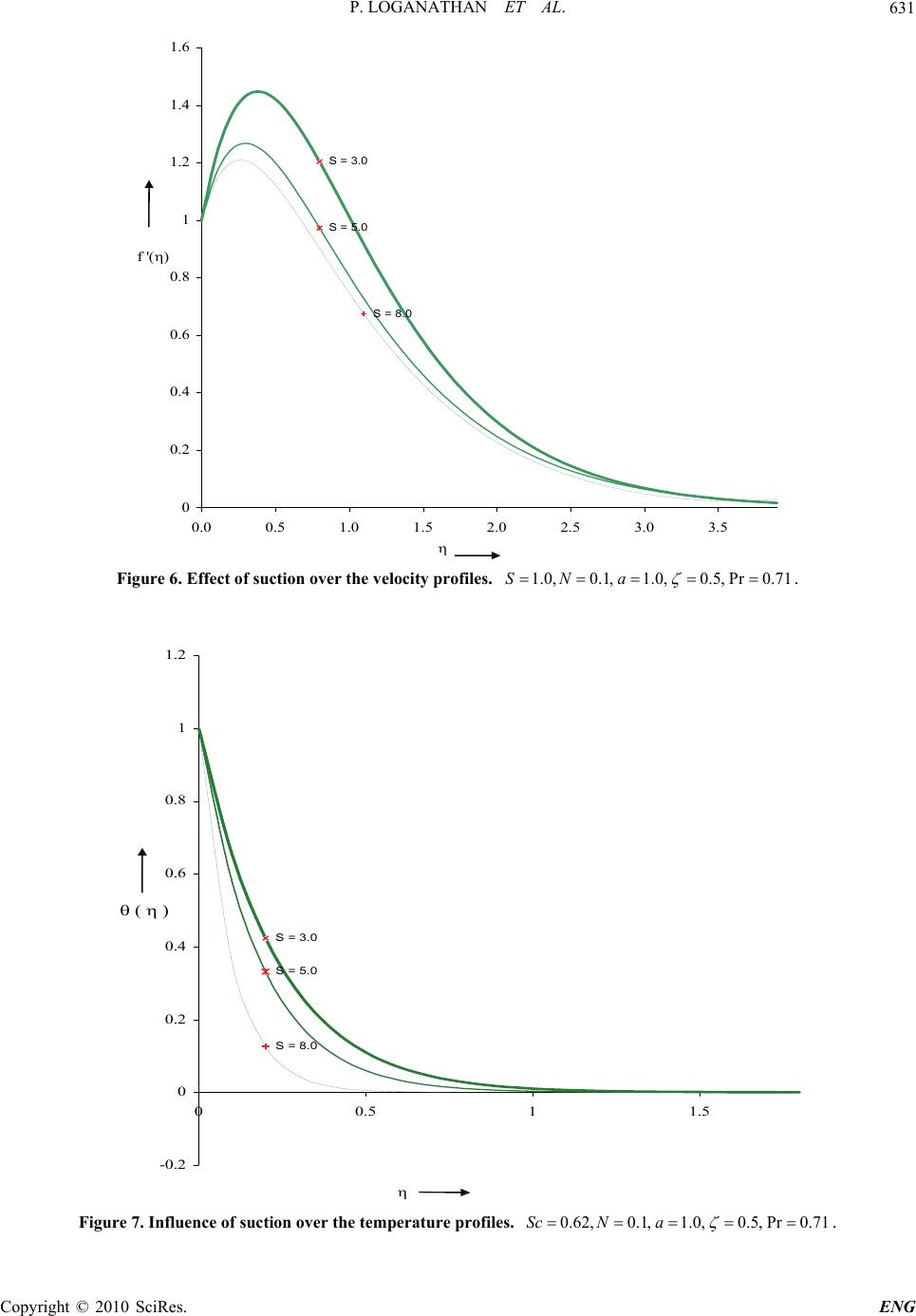

 (  )


P. LOGANATHAN ET AL. 631
S = 3.0
S = 5.0
S = 8.0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5

f '()
Figure 6. Effect of suction over the velocity profiles. 1.0,0.1,1.0,0.5,Pr0.71SNa


 .
S = 3.0
S = 5.0
S = 8.0
-0. 2
0
0.2
0.4
0.6
0.8
1
1.2
0 0.5 1 1.5

 ( )
Figure 7. Influence of suction over the temperature profiles. 0.62,0.1,1.0,0.5, Pr0.71ScNa
 
.

P. LOGANATHAN ET AL. 632
S = 3.0
S = 5.0
S = 8.0
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
00.511.5

 ( )
Figure 8. Effects of Suction over the concentration profiles. 0.62,0.1,1.0,0.5, Pr0.71ScNa
 
.
Sc = 0.22
Sc = 0.62
Sc = 0.78
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
00.511.5

 ( )
Figure 9. Effects of Schmidt number over the concentration profiles. 1.0,0.1,1.0,0.5, Pr0.71SNa  .

P. LOGANATHAN ET AL. 633
the divergence of the radiative heat flux r
q
y

increases
as  decreases which in turn increases the rate of radia-
tive heat transferred to the fluid and hence the fluid tem-
perature increases. In view of this explanation, the effect
of radiation becomes more significant as N→ 0 (N ≠
0) and can be neglected when N → ∞. Also, it is seen
from Figure 3 that the larger theN, the thinner the
thermal boundary layer thickness for both values ofPr .
In addition, radiation demonstrates a more pronounced
influence on the temperature distribution of (Pr 0.3

)
than that of (Pr 1.0).It is noticed from the figure that
the temperature decreases with the increasing value of
the radiation parameterN. The effect of radiation pa-
rameter N is to reduce the temperature significantly in
the flow region. The increase in radiation parameter
means the release of heat energy from the flow region
and so the fluid temperature decreases as the thermal
boundary layer thickness becomes thinner.
Figure 4 exhibits the velocity profiles for several val-
ues of

with Pr = 0.71 in presence of suction (S = 0.5)
when N= 0.1. In the case of uniform suction, the veloc-
ity of the fluid is found to increase with the increase of
the temperature-dependent fluid viscosity parameter

at a particular value of

except very near the wall as
well as far away of the wall (at

= 5). This means that
the velocity decreases (with the increasing value of

) at
a slower rate with the increase of the parameter

at
very near the wall as well as far away of the wall. This
can be explained physically as the parameter

in-
creases, the fluid viscosity decreases the increment of the
boundary layer thickness.
In Figure 5, variations of temperature field ()

 with

for several values of

(with Pr = 0.71 and N = 0.1)
in presence of suction (S = 0.5) are shown. It is very
clear from the figure that the temperature decreases with
the increasing of

whereas the concentration of the
fluid is not significant with the increasing of

. The
increase of temperature-dependent fluid viscosity pa-
rameter (

) makes decrease of thermal boundary layer
thickness, which results in decrease of temperature pro-
file )(


. Decrease in ()

 means a decrease in the ve-
locity of the fluid particles. So in this case the fluid par-
ticles undergo two opposite forces: one increases the
fluid velocity due to decrease in the fluid viscosity (with
increasing

) and other decreases the fluid velocity due
to decrease in temperature ()

 (since ()

 de-
creases with increasing

). Near the surface, as the
temperature ()

 is high so the first force dominates and
far away from the surface ()

 is low and so the second
force dominates here. Now we concentrate in the veloc-
ity and temperature distribution for the variation of suc-
tion parameter S in the absence and presence of tem-
perature-dependent fluid viscosity parameter

.
Figure 6 presents the effects of suction on fluid veloc-
ity when the fluid viscosity is uniform, i.e.,

= 0.5.
With the increasing value of the suction (S > 0) (

=
0.5, Pr = 0.71 and N = 0.1), the velocity is found to de-
crease (Figure 6), i.e., suction causes to decrease the
velocity of the fluid in the boundary layer region. The
physical explanation for such a behavior is as follows. In
case of suction, the heated fluid is pushed towards the
wall where the buoyancy forces can act to retard the fluid
due to high influence of the viscosity. This effect acts to
decrease the wall shear stress. Figures 7 and 8 exhibit
that the temperature ()

 and concentration ()

 in
boundary layer also decrease with the increasing suction
parameter S (S > 0) (

= 0.5, Pr = 0.71 and N =
0.1).The thermal and solutal boundary layer thickness
decrease with the suction parameter S which causes an
increase in the rate of heat and mass transfer. The expla-
nation for such behavior is that the fluid is brought closer
to the surface and reduces the thermal boundary layer
thickness in case of suction. As such then the presence of
wall suction decreases velocity boundary layer thick-
nesses but decreases the thermal and solutal boundary
layers thickness, i.e., thins out the thermal and solutal
boundary layers.
Figure 9 illustrates the influence of Schmidt number
Sc on the concentration. As Schmidt number Sc increases,
the mass transfer rates increases. Hence, the concentra-
tion decreases with increasing Sc. It is evident from this
figure that the concentration ()

 takes its limiting
value C∞, for higher values of the dimensionless distance

. From this figure, we observe that when the concen-
tration difference ΔC is maintained constant, the dimen-
sionless concentration profile decreases, in the since that
the values of the Schmidt number increases. The varia-
tion in the thermal boundary layer is very small corre-
sponding to a moderate change in Schmidt number.
There are very small changes in velocity and temperature
distributions when moderate changes in Schmidt number.
5. Conclusions
By using Lie group analysis, first find the symmetries of
the partial differential equations and then reduce the
equations to ordinary differential equations by using
scaling and translational symmetries. Exact solutions for
translation symmetry and numerical solution for scaling
symmetry are obtained. From the numerical results, it is
predict that the effect of increasing temperature-
dependent fluid viscosity parameter on a viscous incom-
pressible fluid is to increase the flow velocity which in

P. LOGANATHAN ET AL. 634
turn, causes the temperature to decrease. It is interesting
to note that the temperature of the fluid decreases at a
very fast rate in the case of water in comparison with air.
So, the thermal radiation effects in the presence of fluid
viscosity have a substantial effect on the flow field and,
thus, on the heat and mass transfer rate from the sheet to
the fluid. Decrease of the concentration field due to in-
crease in Schmidt number shows that it increases gradu-
ally as we replace Hydrogen (Sc = 0.22) by water vapour
(Sc = 0.67) and Ammonia (Sc = 0.78) in the said se-
quence.
6. References
[1] L. J. Crane, “Flow Past a Stretching Plate,” The Journal
of Applied Mathematics and Physics, Vol. 21, No. 4, pp.
645-647.
[2] 1. H. I. Andersson, J. B. Aarseth and B. S. Dandapat,
“Heat Transfer in a Liquid Film on an Unsteady Stretch-
ing Surface,” International Journal of Heat and Mass
Transfer, Vol. 43, No. 1, 2000, pp. 69-74.
[3] C. Y. Wang, “Liquid Film on an Unsteady Stretching
Surface,” Quarterly of Applied Mathematics, Vol. 48, No.
4, 1990, pp. 601-610.
[4] P. Saikrishnan and S. Roy, “Non-Uniform Slot Injection
(Suction) into Steady Laminar Water Boundary Layers
over (i) a Cylinder and (ii) a Sphere,” International
Journal of Engineering Science, Vol. 41, No. 12, 2003,
pp. 1351-1365.
[5] S. Roy and P. Saikrishnan, “Non-Uniform Slot Injection
(Suction) into Steady Laminar Water Boundary Layer
Flow over a Rotating Sphere,” International Journal of
Heat and Mass Transfer, Vol. 46, No. 18, 2003, pp.
3389-3396.
[6] E. M. A. Elbashbeshy and M. A. A. Bazid, “Heat Trans-
fer in a Porous Medium over a Stretching Surface with
Internal Heat Generation and Suction or Injection,” Ap-
plied Mathematics and Computation, Vol. 158, No. 3,
2004, pp. 799-807.
[7] P. Cheng and W. J. Minkowycz, “Free Convection about
a Vertical Flat Plate Embedded in a Porous Medium with
Application to Heat Transfer from a Disk,” Journal of
Geophysical Research, Vol. 82, No. 14, 1963, pp. 2040-
2044.
[8] P. Cheng, “The Influence of Lateral Mass Flux on a Free
Convection Boundary Layers in Saturated Porous Me-
dium,” International Journal of Heat and Mass Transfer,
Vol. 20, No. 3, 1977, pp. 201-206.
[9] G. Wilks, “Combined Forced and Free Convection Flow
on Vertical Surfaces,” International Journal of Heat and
Mass Transfer, Vol. 16, No. 10, 1973, pp. 1958-1964.
[10] Y. Z. Boutros, M. B. Abd-el-Malek and N. A. Badran,
“Group Theoretic Approach for Solving Time-Indepen-
dent Free Convective Boundary Layer Flow on a Non-
Isothermal Vertical Flat Plate,” Archives of Mechanics,
Vol. 42, No. 3, 1990, pp. 377-395.
[11] T. S. Chen and F. A. Strobel, “Buoyancy Effects in
Boundary Layer Adjacent to a Continuous Moving Hori-
zontal Flat Plate,” Journal of Heat Transfer, Vol. 102,
1980, p. 170.
[12] N. Ramachandran, B. F. Armaly and T. S. Chen, “Corre-
lation for Laminar Mixed Convection on Boundary Lay-
ers Adjacent to Inclined Continuous Moving Sheets,” In-
ternational Journal of Heat and Mass Transfer, Vol. 30,
No. 10, 1987, pp. 2196-2199.
[13] S. L. Lee and J. S. Tsai, “Cooling of a Continuous Mov-
ing Sheet of Finite Thickness in the Presence of Natural
Convection,” International Journal of Heat and Mass
Transfer, Vol. 33, No. 3, 1990, pp. 457-464.
[14] M. A. Hossain and H. S. Takhar, “Radiation Effect on
Mixed Convection along a Vertical Plate with Uniform
Surface Temperature,” International Journal of Heat and
Mass Transfer, Vol. 31, No. 2, 1996, pp. 243-248.
[15] H. S. Takhar, R. S. R. Gorla and V. M. Soundalgekar,
“Radiation Effects on MHD Free Convection Flow of a
Gas Past a Semi-Infinite Vertical Plate,” The Interna-
tional Journal of Numerical Methods for Heat & Fluid
Flow, Vol. 6, No. 2, 1996, pp. 77-83.
[16] M. A. Hossain, M. A. Alim and D. A. Rees, “The Effect
of Radiation on Free Convection from a Porous Vertical
Plate,” International Journal of Heat and Mass Transfer,
Vol. 42, No. 7, 1999, pp. 181-191.
[17] J. Gary, D. R. Kassoy, H. Tadjeran and A. Zebib, “The
Effects of Significant Viscosity Variation on Convective
Heat Transport in Water-Saturated Porous Media,” Jour-
nal of Fluid Mechanics, Vol. 117, 1982, pp. 233-249.
[18] K. N. Mehta and S. Sood, “Transient Free Convection
Flow with Temperature-Dependent Viscosity in a Fluid
Saturated Porous Medium,” International Journal of En-
gineering Science, Vol. 30, No. 8, 1992, pp. 1083-1087.
[19] S. Mukhopadhyay, G. C. Layek and S. A. Samad, “Study
of MHD Boundary Layer Flow over a Heated Stretching
Sheet with Variable Viscosity,” The International Jour-
nal of Numerical Methods for Heat & Fluid Flow, Vol.
48, No. 21-22, 2005, pp. 4460-4466.
[20] S. Mukhopadhyay and G. C. Layek, “Effects of Thermal
Radiation and Variable Fluid Viscosity on Free Convec-
tive Flow and Heat Transfer Past a Porous Stretching
Surface,” International Journal of Heat and Mass Trans-
fer, Vol. 51, No. 2, 2008, pp. 2167-2178.
[21] M. Q. Brewster, “Thermal Radiative Transfer Proper-
ties,” John Wiley and Sons, Chichester, 1972.
[22] G. K. Batchelor, “An Introduction to Fluid Dynamics,”
Cambridge University Press, London, 1987.
[23] J. X. Ling and A. Dybbs, “Forced Convection over a Flat
Plate Submersed in a Porous Medium: Variable Viscosity
Case Paper 87-WA/HT-23,” American Society of Me-
chanical Engineers, New York, 1987.
[24] S. Gill, “A Process for the Step-by-Step Integration of
Differential Equations in an Automatic Digital Comput-
ing Machine,” Proceedings of the Cambridge Philoso-
phical Society, Vol. 47, No. 1, 1951, pp. 96-108.