Paper Menu >>
Journal Menu >>
 J. Mod. Phys., 2010, 1, 163-170 doi:10.4236/jmp.2010.13024 Published Online August 2010 (http://www.scirp.org/journal/jmp) Copyright © 2010 SciRes. JMP Quantum Statistical Properties of Resonant Radiation Scattered on Excited Systems Boris A. Veklenko Joint Institute for High Temperatu r e of Russian Academy of Science, Moscow, Russia E-mail: VeklenkoBA@yandex.ru Received April 15, 2010; revised May 21, 2010; accepted June 10, 2010 Abstract The scattering of resonant radiation on an excited atom is considered. It is shown that the scattering cross section calculated with the help of quantum theory of radiation is five times larger than the one calculated using semi-classical theory. The quantum theory predicts, in general, the change in internal quantum statisti- cal properties of light due to the scattering processes on excited atoms. Keywords: Quantum Theory, Semi-Classical Theory, Resonant Radiation 1. Introduction The quantum excited systems possess remarkable prop- erties. They manifest themselves most prominently in lasers and masers, which were created in the middle of the last century. The theory of these devices was elabo- rated by W. Lamb [1] on the base of a semi classical theory of radiation which deals with classical electro- magnetic field. Later the quantum theory was proposed [2]. It is possible to state omitting the fluctuations prop- erties that both the semi classical and the quantum theo- ries result practically in the same results for quantum means values. Such a fact resulted in overestimation of the applicability of the semi-classical theory. In 1966 year, Ch. Koester predicted the effect of light enhance- ment [3] by selective reflection of resonant radiation from excited media. All efforts of quantitative ex plaining this effect on the base of semi-classical theory of radia- tion discussed in monograph [4] were unsuccessful [5,6]. It was shown later that quantum field theory should be used instead [7], but the mathe matically problems on th is way occurred very difficult [8]. The consequences of such a theory manifest themselves on a macroscopic level. The correct description of stimulated radiation plays an especial role when the resonant reflection of light from excited media is considered. Nevertheless, there are recent works [9] which make use the semi- classical theory and Fresnel’s formulae to describe the reflection of light from enhanced media. Much attention has been paid recently to the effect of the enhanced transmission of light through the metallic films [10,11]. There is no agreement between theory and experiment. It is believed that the enhancement of radia- tion may be explained through the interaction of light with induced standing surface—plasmon waves. Thus we deal with effects of stimulate radiation, which means that one should use the quantum field theory. Examples shown above made us revise the theory of resonant radiation scattering on excited systems. The conventional perturbation technique is not adequate to describe the resonant scattering and it is necessary to sum up (Dyson summation) the infinitely long subsets of Feynman’s ladder diagrams. It was V. Weissk opff and E. Wigner who constructed such a theory for the first time by considering the interaction of resonant radiation with atomic systems [12]. Such a summation of Feynman’s diagram proved to be useful for the shape of spectrum line of resonant radiation and effects of resonant light scattering on non excited systems. The difficulties emerge in the theory of combined resonant scattering processes when one of the photons after stimulation emi- ssion of excited atom undergoes of elastic scattering on the ground state of the same atom. Such combined scat- tering is non-analytic in charge. The summation of the Feynman’s diagrams like this one is not performed up to now [8]. We propose indirect way to estimate this sum. Present work demonstrates insufficiency Weisskopff- Wigner’s method and Dyson’s method of summation Feynman’s ladder diagrams for the calculations the cross-sections of light scattering on resonant excited systems and failure of semi-classical theory of radia tion. Let the resonant radiation scatters on some system the initial state of which in interaction representation is de- scribed by wave function 0 . The total wave function of electromagnetic field and scattering system is denoted as . The expansion of such function over a base of scattering system wave function i is  B. A. VEKLENKO Copyright © 2010 SciRes. JMP 164 0000 00 0ii i fff f . The term containing 0 is written separately. The scalar product due to orthogonality of scatter’s wave functions 0000 0ff is equal to zero. Assume that the incident light is in quantum coherent state [13] and its quantum mean elec- trical strength is not equal to zero ˆ(,)0t rEin all space points r at arbitrary instant of timet. We are interesting in quantum mean value of operator ˆ E of the reflected light 0000 0000 () () ˆˆ (,) (,) ˆˆ (,) (,) cn tt ftf ftf rr rr EE EE EE (1) We state that the first term of the right hand side of Equation (1) describes the so-called coherent scattering channel with medium returning to the initial quantum state after scattering (e.g. elastic scattering). The second term of the right hand side of Equation (1) describes the non-coherent scattering processes with the medium changing initial quantum state (Compton scattering, Ra- man scattering and induced radiation of light). The latter is very important. We stress once again that the coherent Heisenber-Kramers scattering and induced radiation of light are described by different scattering channels. It means that if the scattering media consisted only of the non-excited atoms the first term of Equation (1) would describe the coherent Heisenberg-Kramers scattering while the second one would describe the diffusion scat- tering. If the excited atoms are present in the medium then due to the induced radiation processes it is impossi- ble to avoid the presence of the non-coherent channel even if only the selective scattering is under our investi- gation. The total measured electrical strength ˆ(,)t rE, that is the left hand part of Equation (1), may be evalu- ated separately using the semi-classical theory of radia- tion if one neglects the fluctuation optical processes and their influence on ˆ(,)t rE. The region of validity of the semi-classical theory of radiation is very large but it does not mean that ˆ(,)t rE describes the bilinear field characteristics. Let us consider the energy characteristics of electro- magnetic field described by normal operator product 2 ˆˆ N E. Such value should be estimated from below using the following procedure. One takes into account that ˆˆˆ (,) 2 i ickti ickt ck tie ee V kr kr kk k k r E, where ˆ k and ˆ k are the annihilation and creation photon operators in states describing by wave vector k and polarization index . These operators obey the conventional commutation relations ˆˆ ; kkkk Consider electromagnetic field as a transverse one(1,2) , k e denotes the unite linear polarization vectors, V is the quantization volume. Since the op- erators ˆ k and ˆ k are mutual conjugate than ()() ˆˆ ˆˆ0 i ickkt ekek e kkr kkkkkk kk Now ()() ˆˆ i ickkt kk eee kkr kkkk kk ()() ˆˆiickkt kk eee kkr kk kk kk If the electromagnetic field possesses the characteristic frequency 0 and characteristic wave length 0 and we are interesting in time and space values much larger then 0 1/ and 0 the following in equality occurs ()() ˆˆ i ickkt kk eee kkr kkkk kk ()() ˆˆ iickkt kk eee kkr kkk k kk ()() ˆˆ iickkt kk eee kkr kkk k kk ()() ˆˆ iickkt kk eee kkr kkk k kk Now it is non difficult to see that 2 ˆˆ (,)Nt rE () () ˆˆ iicktt ckk eee V kkr kkkk kk () () 2 ˆˆ ˆ(,) iicktt ckk eee V t kkr kk kk k r E (2) Thus ˆ E proposes the opportunity to estimate  B. A. VEKLENKO Copyright © 2010 SciRes. JMP 165 2 ˆˆ N Efrom below. The validity of obtained ine- quality does not depend on particular quantum state on which the averaging is performed and does nothing to do with perturbation theory. But if such ineq uality is app lied to each term of right hand site of 22 00 00 2 00 00 ˆˆ ˆˆ () () ˆˆ () NfNf fN f EE E (3) We find that 2 22 00000000 ˆˆ () ˆˆ N fff f E EE The last formula can be rewritten in as 2 2 2 00000000 ˆˆ () ˆˆˆ N ff ff E EEE (4) That stresses the importance of the coherent scattering channel when the scattered light is not classical and. 2 2 ˆˆ ˆ () N EE. Inequality (4) allows to estimate 2 ˆˆ () N Ein the semi-classical approximation. The value ˆ EE can be calculated using the conventional semi-classical theory operating with non quantum electromagnetic field. The calculation () 00 00 ˆ c ff EE can be per- formed using only the coherent scattering channel. Even in extensive media such procedure may be performed with the help of wave functions [14]. Thus one can avoid of matrix density formalism specific for non coherent scattering chan nel . 2. Principal Equations Let the electromagnetic field scatters on an atom situated at a point with radius-vector Rand for the sake of sim- plicity possesses only one orbital electron with coordi- nate r. Let the atom possesses only two energy levels. Zeeman`s sublevels with different magnetic numbers are possible. Let the frequency of incident radiation is in a quasi resonance 00 with th e atom transition frequency 0 . Let Schroedinger equation for atom and radiation is as follows ˆˆ ˆ aph iHHH t , where 2 ˆ ˆˆˆ ()() () 2 ap H Ud m r rrRrr ˆ ˆˆˆ ˆ ()() () e H pA d mc r rrrr are the Hamiltonian of the non-interacting atoms and an interaction Hamiltonian in Schroedinger representation. Than ˆ ˆ()( ) j j j b rrR, ˆ ˆ()( ) j j j b rrR, ˆ pi rr . The following communitation relations are assumed ˆˆ ; j jjj bb for the electron creation operator ˆ j b and annihilation operator ˆ j b in the state described by wave function j . The particular form of communication relations in our case of one electron in the atom does not play any role. By ()U rRwe denote the potential energy of atom electron. The Einstein summation rule is assumed over all repeating indices throughout the paper. The Ham- iltonian of free electromagnetic field and vector-potential operator are as follows ˆˆˆ ph Hck kk k ˆˆˆ () 2 ii c Aeee kV kr kr kk k k r In order to realize the calculation project mentioned in introduction we switch to the interaction representation with the help of unitary operator 1 ˆˆˆ () exp() aph UtHH t i . In this picture 00 ˆ () ,tStt , 01 ˆˆˆ ,exp () t Stt THtdt i (5) ˆ ˆˆˆ ˆ ()()() () e H txpAxxd mc rr, , x tr, ˆ ˆ()() j it j j j x eb rR ˆ ˆ()() j it j j j x eb rR . where 0 ˆ,Stt is the scattering operator, j is the atomic energy in state j , ˆ T is the time-ordering op- erator and  B. A. VEKLENKO Copyright © 2010 SciRes. JMP 166 () () ˆˆ ˆ ()()() ˆˆ 22 i ikcti ikct AxAx Ax cc ee ee kV kV kr kr kk kk kk (6) 3. Coherent Scattering Channel Suppose that the initial state of the field was described by 00 (,) k and was in quantum coherent state [13] 2 00 1 02 0 ˆ () 0 ! n n fe n k. The amplitude of initial radiation was 00 00 00 0000 00 00 0000 ˆˆ () () , iikctiikct AxfAxf eae ae kr kr kk k 00 2 c akV k . We are interested in the radiation amplitude after scat- tering in second order of perturbation technique. The problem of Feynman’s diagrams summation will be dis- cussed below. In Equation (5) it is sufficient to consider the sum (1) (2)(3) ˆˆˆˆ 1SSSS , where (1) 1 ˆˆ()SHtdt i 2 (2) 2 ˆ ˆˆ() 2( ) T SHtdt i , 3 (3) 3 ˆ ˆˆ() 3!() T SHtdt i . If the photon scatters in the coherent channel then the atom rests in initial state. So in second order of perturba- tion technique we are interested in the cons truction () (2) 00 ˆˆ () ().. c x AxS cc A (7) We change the time-ordering product of the atom op- erators by the normal ordering one. For the scattering operator (2) ˆ S we get 12 12 12 (2) 2 1112 2212 ˆ ˆˆˆ ˆˆ ˆˆ ()() (, )()() Ar S T e x pAxGxxpAxxdxdx mc i rr where ˆA Tis the time-ordering operator acting only on the electromagnetic field operators and 12 ˆˆ ˆˆ ()( )(,) r TNxx iGxx , 12 12 () 12 (, ) ()()2 r Ett j jj r j Gxx EdE eG rRr R 1 0 j rj E GEi (8) If the atom undergoes the action of external random fields the finite width of its energy levels can be taken into account by replacing the term 0iby /2 j i with the same sign because it is governed by the causal- ity principle. The same result follows from summing up (Dyson summation) the ladder Feynman`s diagrams for excited atoms due to their interaction with electromag- netic vacuum. For the same reason formula (8) can be written as 1 2 j r j j E G Ei . without specifying the value j . We take into account that, 12 1212 12 1212 ˆˆ ˆ() () ˆˆ ˆ (, )()() A TAx Ax iDxxNAx Ax (9) where 12 12 (, )Dxx is not the operator function. The first term in (9) does not play any role in electromagnetic field scattering process. Finitely 12 12 21 12 2 (2) 112 () ()() () 211 2212 1 ˆˆˆˆ ()(, ) ˆˆˆˆ ˆ ()()()() () r e SxpGxxp imc A xAx AxAxxdxdx rr (10) The right hand side terms of this equality are respon- sible on scattering processes of electromagnetic field by both the non excited atom and excited one. 3.1. Scattering on Non-Excited Atom Substituting (6) and (8) into Equation (10) and taken the limit t, we find 12 1012 00 11 022011 00 2 211 02 2 0 0 10 () (2) 00 00 00 ˆˆ ˆˆ 2 i jj jj jjj jjj kc kc ce Sfppbbe eef iVk mckc i Rk k k kk k  B. A. VEKLENKO Copyright © 2010 SciRes. JMP 167 Through 0 j one denote here the quantum number of initial state of atom. In dipole approximation 020ˆ () () jj j ppd ρ ρρρ. The limit t is not necessary but it makes the calculations simpler. According to (7) we need to calcu- late the construction 00 ()()(2) 00 00 ˆˆ ()() .. c x fAxSf cc A Let us use the following equalities connecting any smooth function () f k and limits V, rR 11 11 11 11 () 101 () i ee kckcefk krR kk k 1 11 1 1 () 10 11 3 0 00 2 () (2) sin () 2 i Vekckcfkd rr k Vkfk nn krR k rR rR where n rR rR Here we take into account only the term describing diverge wave. The neglected term turns into zero by infi- nitely small interval of integration over 0 k that is sup- posed. Finitely 1 100 0122 00 02 2000 22 2 () 00 11 () .. 4 2 ikik ct i cjj jjjj nn e x ae ppeecc mc ck i rR kR kk rR A (11) 3.2. Scattering on Excited Atom The second term in Equation (10) after the same type of transformation sho w n in part 3. 1 yi elds 2 200 012 1 00 02 2000 22 2 () 00 11 () .. 4 2 ikik ct i cjj jjjj nn e x ae ppeecc mc ck i rR kR kk rR A (12) If one takes into account the width of atom’s energy level in state described by 0 j than it is necessary to replace 202 j jj in Equation (12). The va- lidity of Equations (11) and (12) are restricted by domain /1 r where r is the radiation width of excited state of atom. 4. Non Coherent Scattering Channel The second order perturbation technique gets 00 ()(1) (1) 00 0 ˆˆ ˆ () () nxfSAxSf A. Or by taken into account only the scattering processes we have in explicit form 12 12 12 200 () () () () 00 1200 2 1ˆˆ ˆ ˆˆˆ ˆ ˆˆ () .. () ne x fpAdxApAdxfcc mc i rr A Follo win g the procedures described in part 3 .1 we have 2 202 00 012 1 00 02 2000 2 2 () 0 () .. 2 jj ikik ct i njj jj j nn ie x ae ppkceecc mc rR kR kk rR A (13) If we take into account the finite width of atom energy level than in formula (13) it is necessary to change 02 02 02 0 00 11 222 jj jj jj kc ikc ikc i  B. A. VEKLENKO Copyright © 2010 SciRes. JMP 168 Let us find now the total amplitude of electromagnetic field scattered by excited atom 2 200 012 1 00 02 2000 2 2 () () 00 11 ()() ().. 42 ikik ct i cn jj jj j nn e x xxaeppee cc mc ck i rR kR kk rR AA A (14) 5. Semi-Classical Theory of Radiation The set equations for field operators () x and () A x in Heisenberg representation is the following 2 () ˆˆ ( )()() 2 x it pe UAxpx mmc r r rR , 1 ()() A xjx c , ˆˆ () 2 e jxp p m rr . This set equations is equivalent to the one mentioned at part 3. Now 1 1 1 011 11 ˆ ()()(,)()( ) r e A xAxxxxp xdx mc r.(15) Here 0() A x is given by the formula (6) and 11 1 1 0 0 111 11 1 1 (,)();()() () 4 r x xAxAxtt i nn cct t rr rr ,1 rr . (16) We are interested in the second order perturbation ex- pansion. This mean that the () x operator has be evaluated in the first order of perturbation technique 11 1 01111 ˆ ()()(,)()() r e x xGxxpAxxdx mc r. (17) Substituting (16) and (17) into (15) we find 12 12 12 2 011 122212 ˆ ˆˆ ˆˆ ()()(,)()(,)()( ).. rr e A xAxxxxpGxxpAx xdxdxHc mc rr (18) For the mean values, the same result can be obtained either by averaging (18) with subsequent breaking up the correlators, or using the semi-classical theory. After re- alizing in (18) the substitution 20202 0202 22 2 00 00 00 0 22020 () ()()iikct iikct AxxAxeaeae kr kr kk k A for the scattered fi eld we ha ve 1 100 012 2 00 02 2000 202 2 0 11 () .. 40 ikik ct ijj jj jjj nn e x ae ppeecc mcck i rR kR kk rR A (19) The upper sign describes the scattering of electroma- gnetic field on the non-excited atom while the low one describes the scattering on excited atom. One should take into account the width of atomic energy level by replac- ing in dominator 0i with 02 /2 ()/2 jj ii . By comparing Equation (19) with Equations (11) and (14) we find that in the approximation we used both the quantum theory and the semi-classical theory result in the same expressions for the scattered amplitude () x A. Namely the necessary coinciding in such results leads to the equality of constants in Formulas (19), (11) and (14). 6. Bilinear Field Charasteristics In this part we are interesting in the following construc- tion shown in introduction ˆˆ ˆ ()()Nx x EE . In order to calculate this value in forth order of per- turbation expansion it should use the Formula (3). But it is not worth to do it. The strait calculation shows that for resonant field scattering 0 () the construction (1) (3) 00 ˆˆˆˆ ˆ() ()SNAxAxS , 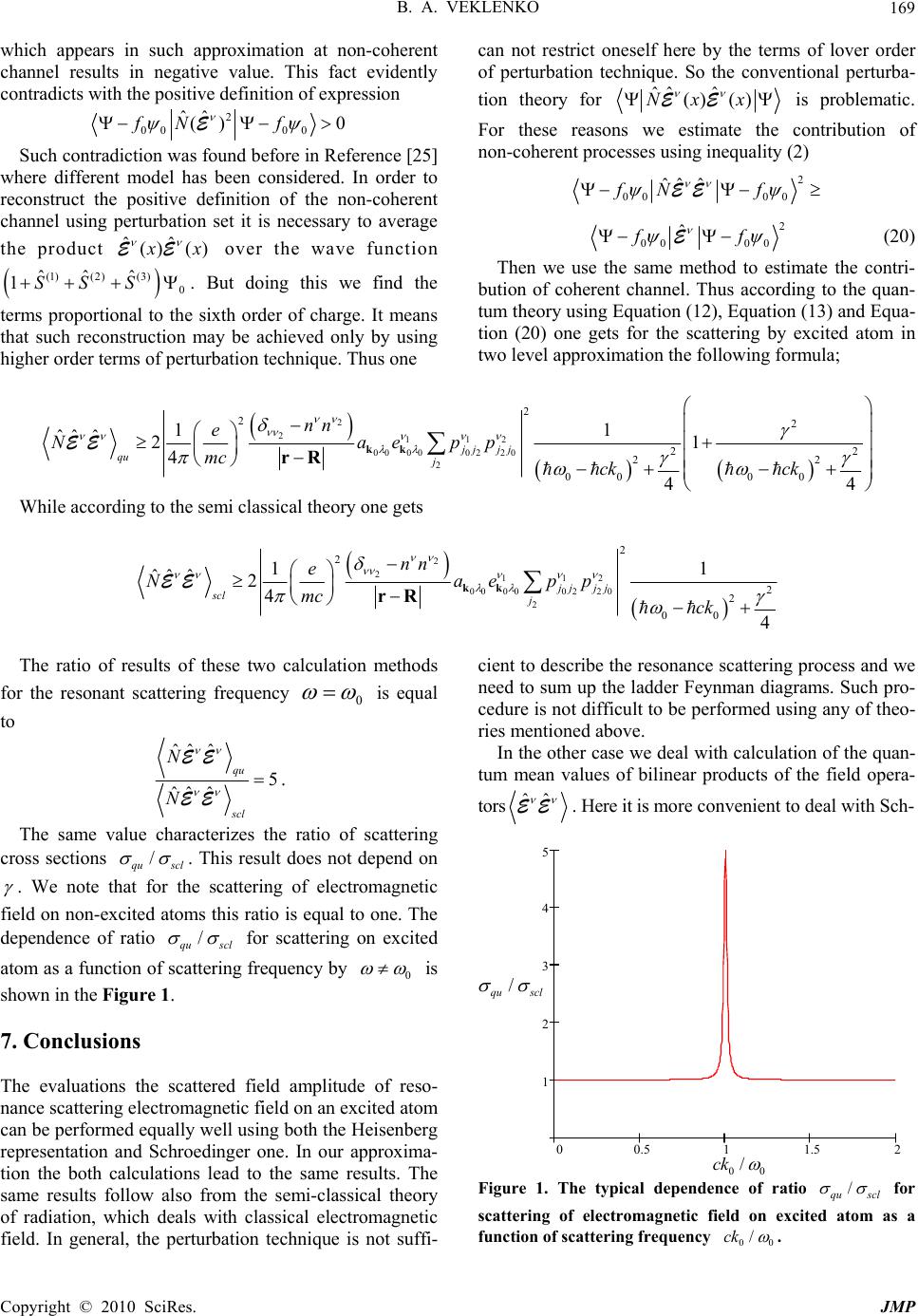 B. A. VEKLENKO Copyright © 2010 SciRes. JMP 169 which appears in such approximation at non-coherent channel results in negative value. This fact evidently contradicts with the positive definition of expression 2 00 00 ˆˆ () 0fN f E Such contradiction was found before in Reference [25] where different model has been considered. In order to reconstruct the positive definition of the non-coherent channel using perturbation set it is necessary to average the product ˆˆ ()() x x EE over the wave function (1)(2)(3)0 ˆˆˆ 1SSS . But doing this we find the terms proportional to the sixth order of charge. It means that such reconstruction may be achieved only by using higher order terms of perturbation technique. Thus one can not restrict oneself here by the terms of lover order of perturbation technique. So the conventional perturba- tion theory for ˆˆ ˆ () ()Nxx EE is problematic. For these reasons we estimate the contribution of non-coherent processes using inequality (2) 2 00 00 ˆˆ ˆ fN f EE 2 00 00 ˆ ff E (20) Then we use the same method to estimate the contri- bution of coherent channel. Thus according to the quan- tum theory using Equation (12), Equation (13) and Equa- tion (20) one gets for the scattering by excited atom in two level approximation the following formula; 2 2112 00 0002 20 2 2 22 22 22 00 00 11 ˆˆ ˆ21 4 44 jj jj qu j nn e Naepp mc ck ck kk rR EE While according to the semi classical theory one gets 2 2112 00 0002 20 2 2 2 2 2 00 11 ˆˆ ˆ24 4 jj jj scl j nn e Naepp mc ck kk rR EE The ratio of results of these two calculation methods for the resonant scattering frequency 0 is equal to ˆˆ ˆ 5 ˆˆ ˆ qu scl N N EE EE . The same value characterizes the ratio of scattering cross sections / qu scl . This result does not depend on . We note that for the scattering of electromagnetic field on non- excited atoms this ratio is equal to one. The dependence of ratio / qu scl for scattering on excited atom as a function of scattering frequency by 0 is shown in the Figure 1. 7. Conclusions The evaluations the scattered field amplitude of reso- nance scattering electromagnetic field on an excited atom can be performed equally well using both the Heisenberg representation and Schroedinger one. In our approxima- tion the both calculations lead to the same results. The same results follow also from the semi-classical theory of radiation, which deals with classical electromagnetic field. In general, the perturbation technique is not suffi- cient to describe the resonance scattering process and we need to sum up the ladder Feynman diagrams. Such pro- cedure is not difficu lt to be performed using an y of theo- ries mentioned above. In the other case we deal with calculation of the quan- tum mean values of bilinear products of the field opera- tors ˆˆ EE . Here it is more convenient to deal with Sch- 0 0.511.52 1 2 3 4 5 Figure 1. The typical dependence of ratio / qu scl for scattering of electromagnetic field on excited atom as a function of scattering frequency 00 /ck . 00 /ck / qu scl  B. A. VEKLENKO Copyright © 2010 SciRes. JMP 170 rödinger representation or with interaction representation, which give additional opportunities to sum up the Feyn- man diagrams. The letter representations allow us to present the scattering process with the help of two com- ponents: coherent (elastic) and non-coherent. Such com- ponents could be evaluated independently. The analysis of non-coherent channel shows that the Dyson’s summa- tion of ladder Fynman’s diagrams by scattering of reso- nant electromagnetic field on excited atoms is not suffi- cient. Other summation methods are very unwieldy [8]. In present work we propose the simple method of esti- mation from below the results of the non-coherent scat- tering channel. As a result we find that the semi-classical theory of radiation essentially underestimates the cross section of resonance scattering. The quantum theory in its turn shows the violation of equality ˆˆ ˆ N EE ˆˆ EE in scattered radiation even if such equality took place in the incident electromagnetic field. So the quantum theory results in a change of quantum statistical structure of electromagnetic field due to scattering. This can not be obtained with the help of semi-classical theory of radiation. This change of internal quantum field stru- cture by its scattering on excited atom manifests itself on macroscopic level. Namely such effect makes impossible using here the semi-classical theory of ra diation. 8. References [1] W. E. Lamb, “The Theory of Optical Masers,” In: C. DeWitt, A. Blandin and C. Cohen-Tannoudji, Eds., Quantum Optics and Electronics, University of Grenoble, Houches, New York-London-Paris, 1965. [2] M. O. Scully and W. E. Lamb, “Quantum Theory of a Optical Masers,” Physical Review Letters, Vol. 159, No. 2, 1967, pp. 208-226. [3] C. J. Koester, “9A4-Laser Action by Enhanced Total Internal Reflection,” IEEE Journal of Quantum Elec- tronics, Vol. QE-2, No. 9, 1966, pp. 580-584. [4] B. B. Boyko and N. S. Petrov, “Reflection of Light from Enhanced and Non Linear Media,” Nauka and Technika, Minsk, 1988. [5] R. F. Cybulski and C. K. Carniglia, “Internal Reflection from fn Exponential Amplifying Region,” Journal of the Optical Society of America, Vol. 67, No. 12, 1977, pp. 1620-1627. [6] T. C. Biba, N. S. Petrov and I. Z. Djilavdary, “The Re- flection of the Light from Non-Homogeneous Medium with Limited Region of Enhancement,” Journal of Ap- plied Spectroscopy, Vol. 32, No. 2, 1980, pp. 226-271. [7] B. A. Veklenko, “Action of the Noise Processes on Inter- ference Properties in Resonance Spektroscopy,” Izvestija Vouzov Physika, No. 9, 1983, pp. 71-75. [8] B. A. Veklenko, R. B.Gusarov and Y. B. Sherkunov, “Selective Reflection of Resonance Radiation from Ex- cited Media,” Journal of Experimental and Theoretical Physics, Vol. 86, No. 2, 1998, pp. 289-298. [9] J. Skaar, “Fresnel Function and the Refractive Index of Active Media,” Physical Review E, Vol. 73, No. 2, 2006. pp. 1-7. [10] I. I. Smolyaninov and Y.-J. Hung, “Enhanced Trans- mition of Light through a Gold Film due to Excitation of Standing Surface-Plasmon Bloch Waves,” Physical Re- view B, Vol. 75, No. 3, 2007, pp. 1-4. [11] T. W. Ebbesen, H. G. Lezec, H. F. Ghaemi, T. Thio and P. A. Wolff. “Extraordinary Optical Transmission through Sub-Wavelength Hole Arrays,” Nature (London), Vol. 391, No. 6668, 1998, pp. 667-669. [12] V. Weisskopf and E. Wigner, “Berechnung der Naturli- chen Linienbreit und Grund der Diracschen Lichttheory,” Zeitschrift fur Physik, Vol. 63, No. 1/2, 1930, pp. 54-73. [13] R. Glauber, “Optical Coherence and Photon Statistics,” In: C. DeWitt. Ed., University of Grenoble, Houches, New York-London-Paris, 1965. [14] B. A. Veklenko, “Remarks on Kramers—Heisenberg Formula and some Properties of induced Radiation,” Iz- vestija Vuzov. Physika, No. 6, 1987, pp. 132-142. |

