J. Intelligent Learning Systems & Applications, 2010, 2, 126-138
doi:10.4236/jilsa.2010.23016 Published Online August 2010 (http://www.SciRP.org/journal/jilsa)
A New Multilevel Thresholding Method Using
Swarm Intelligence Algorithm for Image
Segmentation
Sathya P. Duraisamy, Ramanujam Kayalvizhi
1The Department of Electrical Engineering, Faculty of Engineering and Technology, Annamalai University, Chidambaram, India;
2Department of Instrumentation Engineering, Faculty of Engineering and Technology, Annamalai University, Chidambaram, India.
Received June 11th, 2010; revised June 29th, 2010; accepted July 20th, 2010.
ABSTRACT
Thresholding is a popular image segmentation method that converts gray-level image into binary image. The selection
of optimum thresholds has remained a challenge over decades. In order to determine thresholds, most methods analyze
the histogram of the image. The optimal thresholds are often found by either minimizing or maximizing an objective
function with respect to the values of the thresholds. In this paper, a new intelligence algorithm, particle swarm opti-
mization (PSO), is presented for multilevel thresholding in image segmentation. This algorithm is used to maximize the
Kapur’s and Otsu’s objective functions. The performance of the PSO has been tested on ten sample images and it is
found to be superior as compared with genetic algorithm (GA).
Keywords: Image Segmentation, Multilevel Thresholding, Particle Swarm Optimization
1. Introduction
In many image processing applications, the gray levels of
pixels belonging to an object are substantially different
from those belonging to the background. As such, thres-
holding techniques can be used to extract the objects
from their background. Indeed, thresholding is a major
operation in many image processing applications such as
document processing, image compression, particle coun-
ting, cell motion estimation and object recognition. The
effect of many image processing applications strongly
depends on the effect of image thresholding.
Thresholding techniques provide an efficient way, in
terms of both the implementation simplicity and the pro-
cessing time to perform image segmentation. However,
the automatic selection of a robust optimum threshold
has remained a challenge in image segmentation. Besides
being segmentation on its own, thresholding is frequently
used as one of the steps in many advanced segmentation
methods. In these applications, thresholding is not ap-
plied on the original images, but applied in a space gen-
erated by the segmentation method. For example, in fuzzy
connectedness segmentation [1], a threshold is applied on
the strength of connectedness among image elements to
produce a final segmentation. Thus, the methods to de-
termine effective thresholds have wide-spread applica-
tions. However, automatic determination of the optimum
threshold value is often a difficult task. While a number
of approaches for automatic threshold determination have
been proposed over the past several decades, applying
new ideas and concepts to image thresholding remains an
interesting and challenging research area.
Excellent reviews on early thresholding methods can
be found in [2,3], whereas the latest development in this
topic was summarized in [4]. Comparative performance
studies of global thresholding techniques were presented
by Lee et al. [5]. Otsu [6] proposed a method that maxi-
mizes between-class variance. Tao et al. [7] proposed a
thresholding method for object segmentation based on
fuzzy entropy theory and ant colony optimization algo-
rithm. An image histogram thresholding approaches us-
ing fuzzy sets was proposed by Tobias and Seara [8].
Methods based on optimizing an objective function in-
clude maximization of posterior entropy to measure ho-
mogeneity of segmented Classes [9-11], maximization of
the measure of seperability on the basis of between-
class variance [6], thresholding based on index of fuzzi-
ness and fuzzy similarity measure [12,13], minimization
of Bayesian error [14,15], etc. several such methods have
originally been developed for bi-level thresholding and

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 127
later extended to multilevel thresholding.
Bi-level thresholding divides the pixel into two groups,
one including those pixels with gray levels above a cer-
tain threshold, the other including the rest. Multilevel
thresholding divides the pixels into several groups; the
pixels of the same group have gray levels within a speci-
fied range. However the problem gets more complex
when the segmentation is achieved with greater details
by employing multilevel thresholding. Then the image
segmentation problem becomes a multiclass classifica-
tion problem where pixels having gray levels within a
specified range are grouped into one class. Usually it is
not simple to determine exact locations of distinct valleys
in a multimodal histogram of an image, that can segment
the image efficiently and hence the problem of multilevel
thresholding is regarded as an important area of research
interest among the research communities worldwide.
A great number of thresholding methods of parametric
or non-parametric type have been proposed in order to
perform bi-level thresholding [16] and later extended to
multilevel thresholding [17]. In [18], the Otsu’s function
is modified by a fast recursive algorithm along with a
look-up-table for multilevel thresholding. In [19], Lin has
proposed a fast thresholding computation using Otsu’s
function. Another fast multilevel thresholding technique
has been proposed by Yin [20].
In recent years, several heuristic optimization tech-
niques such as differential evolution (DE), Ant Colony
Optimization (ACO) and Genetic Algorithms (GA) were
introduced into the field of image segmentation because
of their fast computing ability. Erik Cuevas et al. [21]
applied the differential evolution (DE) algorithm to solve
the multilevel thressholding problem. The algorithm fills
the 1-D histogram of the image using a mix of Gaussian
functions whose parameters are calculated using the dif-
ferential evolution method. Each Gaussian function ap-
proximating the histogram represents a pixel class and
therefore a threshold point. Tao et al. [22] proposed the
Ant Colony Optimization (ACO) algorithm to obtain the
optimal parameters of the entropy-based object segmen-
tation approach.
Several techniques using genetic algorithms (GAs)
have also been proposed to solve the multilevel thresh-
olding problem [23,24]. Yin [23] introduced a neighbor-
hood searching strategy in to the GA to speed up the
multilevel thresholds optimization. Though GA-based
approaches perform well for complex optimization prob-
lems, recent research has identified certain deficiencies
[25], particularly for problems in which variables are
highly correlated. In such cases, the GA crossover and
mutation operators do not generate individuals with bet-
ter fitness of offspring as the chromosomes in the popu-
lation pool have some structure towards the end of the
search.
PSO, first introduced by Kennedy and Eberhart [26] is
a flexible, robust, population based stochastic search/opti-
mization algorithm with inherent parallelism. This method
has gained popularity over its competitors and is in-
creasingly gaining acceptance for solving many image
processing problems [27-29]. Compared with other popu-
lation-based stochastic optimization methods such as DE,
ACO and GA, PSO gives superior search performance
with faster and more stable convergence rates [26].
This paper presents a new optimal multilevel thresh-
olding algorithm; Particle Swarm Optimization (PSO) for
solving the multilevel thresholding problem in image
segmentation. The validity of the proposed method is
tested on ten sample images and compared with the GA
method.
2. Problem Formulation
In this paper, two broadly used optimal thresholding
methods namely entropy criterion (Kapur’s) method and
between-class variance (Otsu’s) method are used.
Kapur has developed the algorithm for bi-level thresh-
olding and this bi-level thresholding can be described as
follows:
Let there be L gray levels in a given image and these
gray levels are in a given image and these gray levels are
in the range {0, 1, 2,………,(L-1)}. Then one can define
Pi = h(i)/N, (0 ≤ i ≤ (L-1)) where h(i) denotes number of
pixels for the corresponding gray-level L and N denotes
total number of pixels in the image which is equal to
.

1
0
L
ihi



Then the objective is to maximize the fitness function
f(t) = H0 + H1 (1)
where
1
0
000
In
t
ii
i
PP
Hww


, and
1
0
0
t
i
i
w


P
1
1
11
In
L
ii
it
PP
Hww



,
1
1
L
i
it
wP



The optimal threshold is the gray level that maximizes
Equation (1). This Kapur’s entropy criterion method tries
to achieve a centralized distribution for each histo-
gram-based segmented region of the image.
This Kapur’s entropy criterion method has also been
extended to multilevel thresholding and can be described
as follows: The optimal multilevel thresholding problem
can be configured as a m-dimensional optimization pro-
blem, for determination of m optimal thresholds for a
given image [t1, t2 …tm], where the aim is to maximize
the objective function:
f([t1, t2, ……tm]) = H0 + H1 + H2 +….+ Hm (2)
where

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 128
11
0
000
In
t
ii
i
PP
Hww


,
11
0
0
t
i
i
wP



2
1
1
1
11
In
t
ii
it
PP
Hww



,
2
1
1
1
t
i
it
wP



3
2
1
2
22
In
t
ii
it
PP
Hww



, ,…..
3
2
1
2
t
i
it
wP



1
In
m
L
ii
m
it mm
PP
Hww



, .
1
m
L
mi
it
wP



As Kapur based entropy criterion method, the Otsu
based between-class variance method has also been em-
ployed in determining whether the optimal thresholding
can provide histogram-based image segmentation with
satisfactory desired. The Otsu based between-class vari-
ance algorithm can be described as follows:
If an image can be divided into two classes, C0 and C1,
by a threshold at a level t, class C0 contains the gray lev-
els from 0 to t-1 and class C1 consists of the other gray
levels with t to L-1. Then, the gray level probabilities
( and ) distributions for the two classes are as
follows:
0
w1 w
01
0
00
: , ......
t
PP
Cww
 and 1
1
11
: , ......
tL
PP
Cww

.
where, and
1
0
0
t
i
i
w


P
1
1
L
i
it
wP




Mean levels μ0 and μ1 for classes C0 and C1 are as fol-
lows:
1
0
00
t
i
i
iP
w




,
1
1
1
L
i
it
iP
w




.
Let μT be the mean intensity for the whole image, it is
easy to show that
00 11T
ww

  and
01
1ww
Using discriminant analysis, Otsu based between-class
variance thresholded image can be defined as follows:

01
ft

 
where and

2
000T
w  

L

2
111T
w  
For bi-level thresholding, Otsu selects an optimal
threshold t* that maximizes the between-class variance
f(t);
that is
 
*arg max 0-1tftt
The above formula can be easily extended to multi-
level thresholding of an image. Assuming that there are
m thresholds, (t0, t1, …., tm), which divide the original
image into m classes: C0 for [0, …., t1-1], C1 for [t1, ….,
t2−1] ….. and Cm for [tm, …., L−1], the optimal thresh-
olds


** *
01
, , ....,
m
tt t are chosen by maximizing f(t) as
follows:





***
01 1
, , ...., arg max 0....-1
mm
tttfttt L
(3)
where


012
..... m ft

   
with ,

2
000 T
w  

2
111 T
w  
,

2
222T
w


,…..

2
mmmT
w  .
The Kapur and Otsu methods have been proven as an
efficient method for bi-level thresholding in image seg-
mentation. However, when these methods are extended
to multilevel thresholding, the computation time grows
exponentially with the number of thresholds. It would
limit the multilevel thresholding applications. To over-
come the above problem, this paper proposes the Kapur
and Otsu based PSO algorithm for solving multilevel
thresholding problem. The aim of this proposed method
is to maximize the Kapur’s and Otsu’s objective function
using Equations (2) and (3).
3. Particle Swarm O p t imization (PSO)
PSO is a simple end efficient population-based optimiza-
tion method proposed by Kennedy and Eberhart [24]. It
is motivated by social behavior of organisms such as fish
schooling and bird flocking. In PSO, potential solutions
called particles fly around in a multi-dimensional prob-
lem space. Population of particles is called swarm. Each
particle in a swarm flies in the search space towards the
optimum solution based on its own experience, experi-
ence of nearby particles, and global best position among
particles in the swarm.
3.1 Advantages of PSO
1) PSO is easy to implement and only few parameters have
to be adjusted.
2) Unlike the GA, PSO has no evolution operators such
as crossover and mutation.
3) In GAs, chromosomes share information so that the
whole population moves like one group, but in PSO, only
global best particle (gbest) gives out information to the
others. It is more robust than GAs.
4) PSO can be more efficient than GAs; that is, PSO
often finds the solution with fewer objective function
evaluations than that required by GAs.
Unlike GAs and other heuristic algorithms, PSO has the

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 129
flexibility to control the balance between global and local
exploration of the search space.
3.2 PSO Algorithm
Let X and V denote the particle’s position and its corre-
sponding velocity in search space respectively. At itera-
tion K, each particle i has its position defined by Xi
K =
[Xi,1, Xi,2 ….Xi,N ] and a velocity is defined as Vi
K = [Vi,1,
Vi, 2……Vi, N] in search space N. Velocity and position of
each particle in the next iteration can be calculated as
Vi,n
k+1 = W  Vi,n k + C1  rand1  (pbesti,n – Xi,n k) + C2 
rand2  (gbestn – Xi,n
k)
i = 1, 2………m
n = 1, 2……….N (4)
Xi,n
k+1 = Xi,n k + Vi,n k+1 if Xmin,i,n  Xi k+1  Xmax i,n
= Xmin i,n if Xi,n
k+1  Xmin i,n
= Xmax i,n if Xi,n
k+1 > Xmax i,n (5)
The inertia weight W is an important factor for the
PSO’s convergence. It is used to control the impact of
previous history of velocities on the current velocity. A
large inertia weight factor facilitates global exploration
(i.e., searching of new area) while small weight factor
facilitates local exploration. Therefore, it is better to
choose large weight factor for initial iterations and
gradually reduce weight factor in successive iterations.
This can be done by using
W = Wmax − (Wmax – Wmin) × Iter/Itermax
Where W max and W min are initial and final weight re-
spectively, Iter is current iteration number and Iter max is
maximum iteration number.
Acceleration constant C1 called cognitive parameter
pulls each particle towards local best position whereas
constant C2 called social parameter pulls the particle to-
wards global best position. The particle position is modi-
fied by Equation (4). The process is repeated until stop-
ping criterion is reached.
4. Implementation of PSO for Multilevel
Thresholding Problem
This paper presents a quick solution to the multilevel
image thresholding problems using the PSO algorithm.
The number of threshold levels is the dimension of the
problem. For example, if there are ‘m’ threshold levels,
the ith particle is represented as follows:
Xi = (Xi1, Xi2, ………., Xim)
Its implementation consists of the following steps.
Step 1. Initialization of the swarm: For a population
size p, the particles are randomly generated between the
minimum and the maximum limits of the threshold val-
ues.
Step 2. Evaluation of the objective function: The ob-
jective function values of the particles are evaluated us-
ing the objective functions given by Equation (2) or (3).
Step 3. Initialization of pbest and gbest: The objective
values obtained above for the initial particles of the
swarm are set as the initial pbest values of the particles.
The best value among all the pbest values is identified as
gbest.
Step 4. Evaluation of velocity: The new velocity for
each particle is computed using Equation (4).
Step 5. Update the swarm: The particle position is up-
dated using Equation (5). The values of the objective
function are calculated for the updated positions of the
particles. If the new value is better than the previous
pbest, the new value is set to pbest. Similarly, gbest value
is also updated as the best pbest.
Step 6. Stopping criteria: If the stopping criteria are
met, the positions of particles represented by gbest are
the optimal threshold values. Otherwise, the procedure is
repeated from step 4.
5. Experimental Results and Discussions
In this section, the effectiveness and feasibility of the
proposed PSO method for multilevel thresholding is
demonstrated. Comparisons are performed with the re-
sults provided by GA based multilevel thresholding
method. Tables 1 and 2 represent the various parameters
chosen for the implementation of GA and PSO algo-
rithms respectively. Ten well-known images namely lena,
pepper, baboon, hunter, map, cameraman, living room,
house, airplane and butterfly are taken as the test images,
and are gathered with their histograms in Figure 1.
The quality of the thresholded images for Kapur based
Table 1. Parameters chosen for GA implementation
Parameter Value
Population size 20
No. of Iterations 100
Crossover probability 0.9
Mutation probability 0.1
Selection operator Roulette Wheel Selection
Table 2. Parameters chosen for PSO implementation
Parameter Value
Swam Size 20
No. of Iterations 100
Wmax, wmin 0.4,0.1
C1,C2 2

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 130
(a) (a’)
(b) (b’)
(c) (c’)

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 131
(d) (d’)
(e) (e’)
(f) (f’)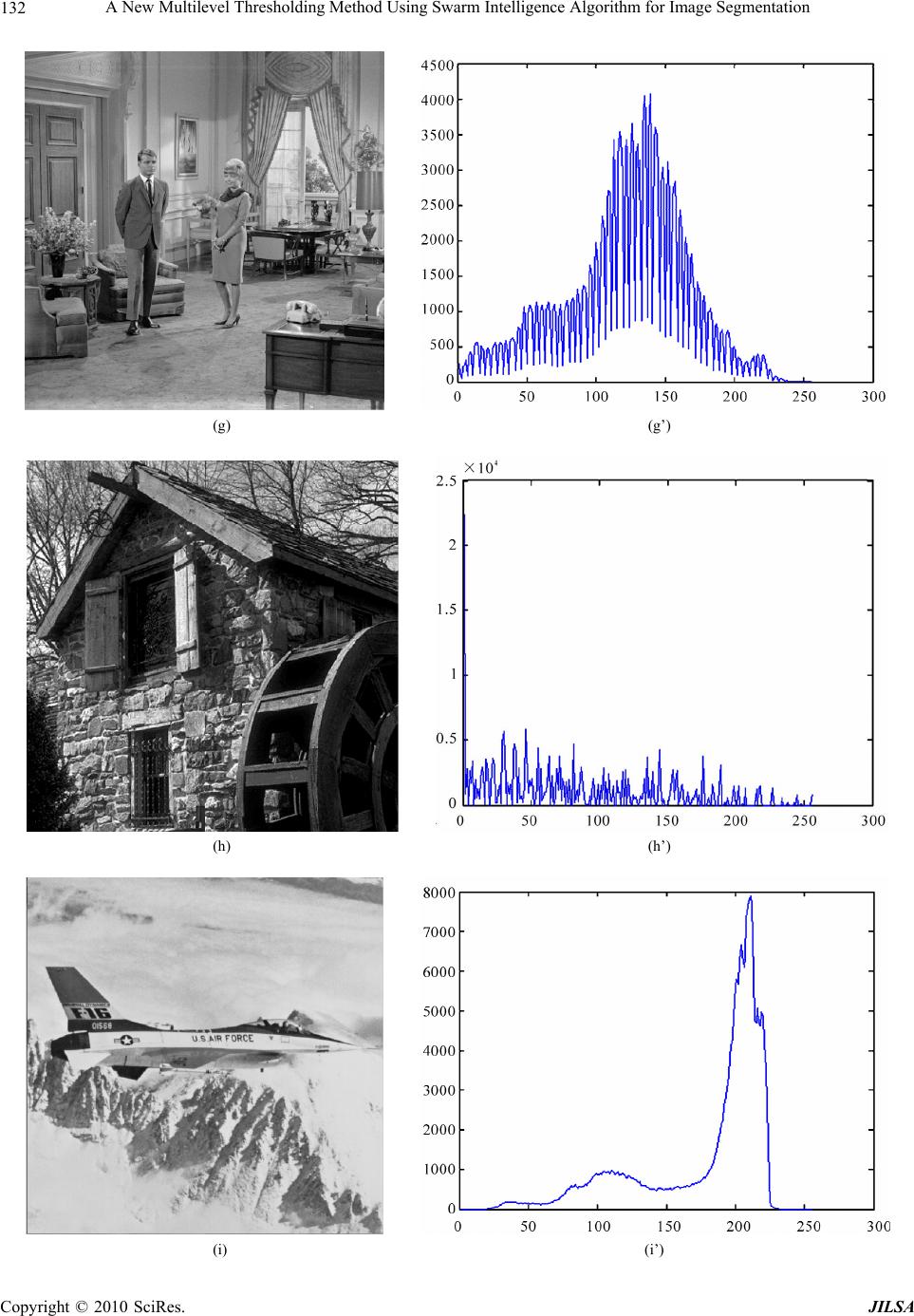

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 132
(g) (g’)
(h) (h’)
(i) (i’)

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 133
(j) (j’)
Figure 1. Test Images and their histograms (a) Lena, (b) Pepper, (c) Baboon, (d) Hunter, (e) Map, (f) Cameraman, (g) Living
room, (h) House,(i) Airplane, (j) Butterfly
(a) (a’) (a’’)
(b) (b’) (b’’)
Figure 2. Thresholded images obtained by Kapur-PSO method ((a), (b) represents 3-level thresholding, (a’), (b’) represents
4-level thresholding, (a’’), (b’’) represents 5-level thresholding)
and Otsu based methods has been evaluated in Tables 3
and 4. The tables show the number of thresholds and the
tive value for PSO and GA methods. It is observed from
the table that in each case, the PSO could perform well as
optimal threshold values with the corresponding objec-compared with the GA method. These two methods use

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 134
Table 3. Comparison of optimal threshold values and objective values obtained by Kapur method
Optimal threshold values Objective values
Test Im
PSO GA
PSO GA
ages m
2 9104,7 12.9 12.4 9,165 16345334
3 86,151,180 72,151,180 15.1336 14.9956
129,191 57,110,4
LENA
7 96,8
72,
PEPPER
0 77,9
0 90,8
BABOON
2 96,7
70,
131,200 64,100,200
HUNTER
9 87,
62,
128,207 96,113,218
MAP
5 85,1
12. 11.
15. 14.
116,2 71,80,
CAMERAMAN
66,9
124,202 74,137,175
LIVINGROOM
60,0
3 83,3
HOUSE
81,9
129,188 87,124,187
AIRPLANE
2 95,6
4 111,3
5 92,116,142,157,182 75,105,140,179,198 16.3374 15.7566
4 92,162,178,1817.8388 17.0892
5 74,115,145,170,19112,151,186,1920.4427 19.5492
2 79,146 82,146
108,
12.5168 12.5133
3 104,141,180 127,186 15.0939 14.7122
4 57,110,162,199 102,172,204 18.0974 17.6959
5 70,116,138,166,20107,124,178,2020.7338 20.0691
2 76,144 93,152
64,
12.2134 12.1847
3 72,130,181 151,181 15.0088 14.7457
4 65,121,153,18106,152,1817.5743 16.9356
5 73,110,142,166,19126,150,172,1920.2245 19.6622
2 83,179 75,178 12.3708 12.3496
3 85,
4 74,
128,166
174,
148,167
189,
15.1286
18.0401
14.8381
17.3189
5 90,120,164,190,2196,128,196,21320.5339 19.5635
2 97,181 84,174 4.9789 4.9610
3 74,
4 92,
140,181
152,
94,156
186,
5.5030
5.6903
5.1351
5.0740
5 66,109,121,150,19114,159,192,215.9165 5.4302
2 115,
3 96,
196
138,191
76,195
111,165,189
2595
2110
9414
8278
4 77,151,20141,192 18.0009 17.1665
5 64,95,121,156,198110,169,180,2020.9631 19.7950
2 86,
3 73,
175
158,187
84,171
74,138,160
12.4000
15.2123
12.3923
14.9700
4 59,172,164,18.1410 17.2063
5 72,97,119,158,197120,148,155,2020.6752 19.8410
2 81,
3 81,
144
116,155
91,145
96,134,164
10.8321
13.1006
10.7436
12.8473
4 75,123,154,19135,170,1915.1027 14.6588
5 48,
2 80,
97,139,159,189
175
107,132,157,18
90,176
17.2517
12.1503
16.9452
12.1153
3 72,121,191 75,110,199 15.2925 14.8059
4 74,162,154,18.0300 17.8923
5 81,118,144,167,19121,141,151,1920.3964 19.4465
2 95,
3 63,
141
126,172
93,142
96,103,167
10.4743
12.3130
10.4707
11.6280
4 71,113,162,18149,155,1714.2317 13.3144
BUTTERFLY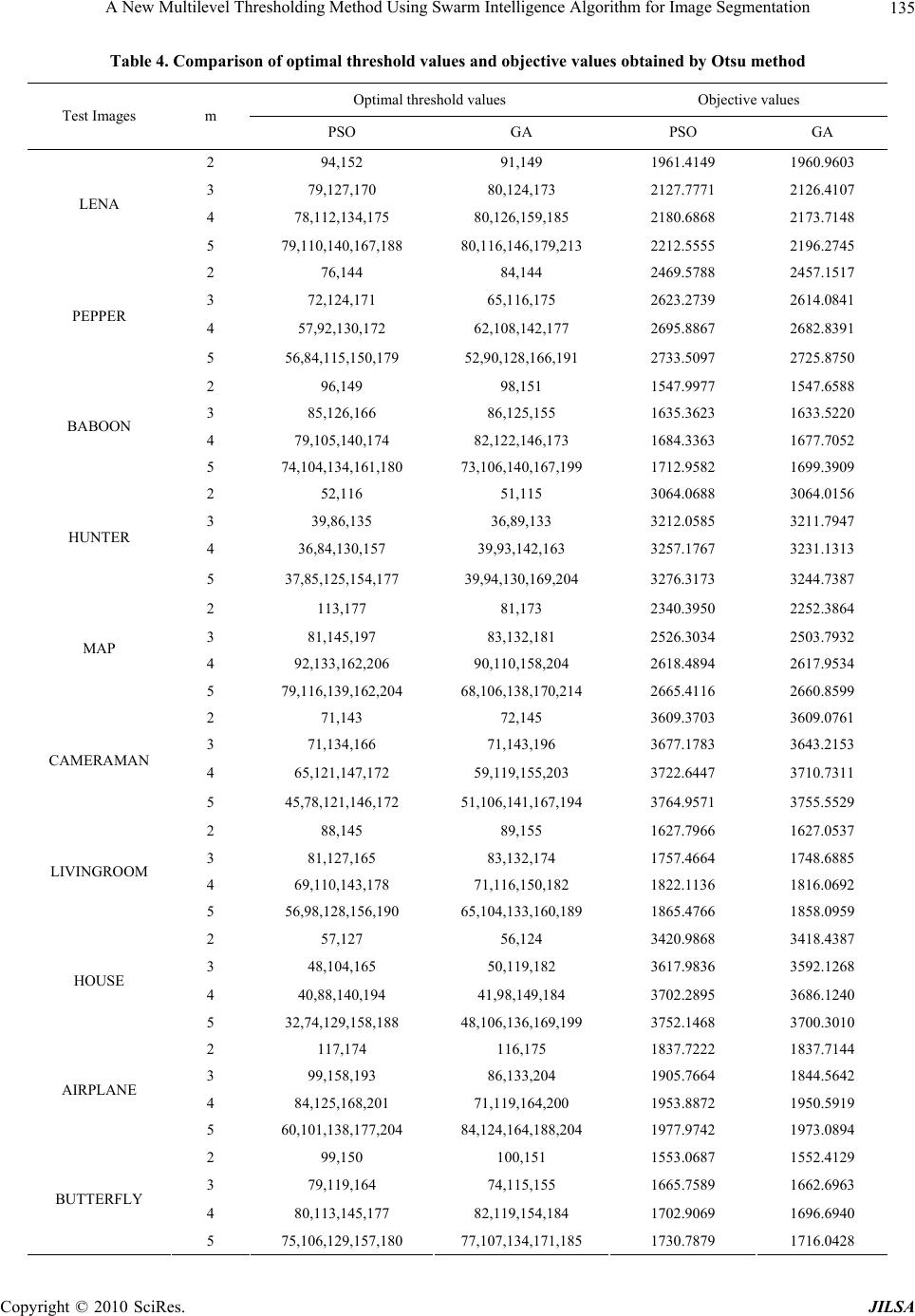

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 135
Table 4. Coparison ofold valuealues obtaOtsu metho
threshojective value
m optimal threshs and objective vined by d
Optimalld values Obs
Test Images m
PSO GA PSO GA
2 94,1,149 1961.40.9603 52 91149 196
3 79,80,73 211 2127
78,15 80,15
LENA
79,18 80,13
57,72 62,17
PEPPER
56,79 52,91
79,14 82,13
BABOON
74,10 73,19
36,57 39,63
HUNTER
37,877 39,904
92,06 90,14
MAP
79,14 68,14
65,12 59,13
CAMERAMAN
45,72 51,14
69,18 71,12
LIVINGROOM
56,90 65,19
40,94 41,84
HOUSE
32,88 48,19
84,01 71,00
AIRPLANE
60,14 84,14
80,17 82,84
BUTTERFLY
75,10 77,15
127,170 124,127.7776.410
4 12,134,1726,159,182180.6868 2173.7148
5 10,140,167,1816,146,179,212212.5555 2196.2745
2 76,144 84,144 2469.5788 2457.1517
3 72,124,171 65,116,175 2623.2739 2614.0841
4 92,130,108,142,172695.8867 2682.8391
5 84,115,150,190,128,166,12733.5097 2725.8750
2 96,149 98,151 1547.9977 1547.6588
3 85,126,166 86,125,155 1635.3623 1633.5220
4 05,140,1722,146,171684.3363 1677.7052
5 04,134,161,1806,140,167,191712.9582 1699.3909
2 52,116 51,115 3064.0688 3064.0156
3 39,86,135 36,89,133 3212.0585 3211.7947
4 84,130,193,142,13257.1767 3231.1313
5 5,125,154,14,130,169,23276.3173 3244.7387
2 113,177 81,173 2340.3950 2252.3864
3 81,145,197 83,132,181 2526.3034 2503.7932
4 133,162,210,158,202618.4894 2617.9534
5 16,139,162,2006,138,170,212665.4116 2660.8599
2 71,143 72,145 3609.3703 3609.0761
3 71,134,166 71,143,196 3677.1783 3643.2153
4 21,147,1719,155,203722.6447 3710.7311
5 78,121,146,106,141,167,193764.9571 3755.5529
2 88,145 89,155 1627.7966 1627.0537
3 81,127,165 83,132,174 1757.4664 1748.6885
4 10,143,1716,150,181822.1136 1816.0692
5 98,128,156,104,133,160,181865.4766 1858.0959
2 57,127 56,124 3420.9868 3418.4387
3 48,104,165 50,119,182 3617.9836 3592.1268
4 88,140,198,149,13702.2895 3686.1240
5 74,129,158,106,136,169,193752.1468 3700.3010
2 117,174 116,175 1837.7222 1837.7144
3 99,158,193 86,133,204 1905.7664 1844.5642
4 125,168,2119,164,21953.8872 1950.5919
5 01,138,177,2024,164,188,201977.9742 1973.0894
2 99,150 100,151 1553.0687 1552.4129
3 79,119,164 74,115,155 1665.7589 1662.6963
4 13,145,17119,154,11702.9069 1696.6940
5 06,129,157,1807,134,171,181730.7879 1716.0428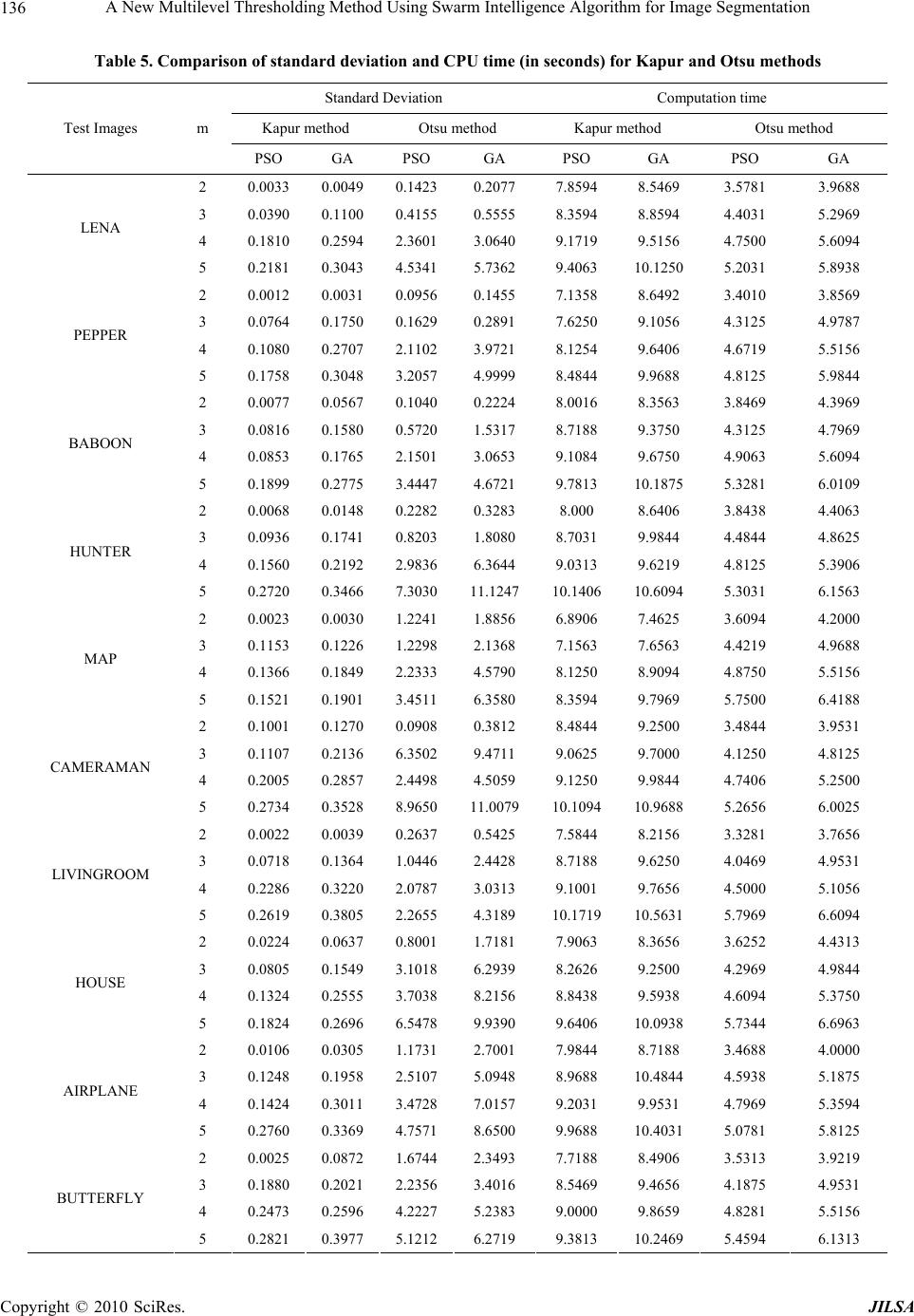

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 136
Table 5. Comparison of standard deviation and CPU ds) for Ktsu met
ation n time
time (in seconapur and Ohods
Standard DeviComputatio
Kapur method Otsu method Kapur method Otsu method
Test
PSO GA PSO GA PSO GGA
Images m
A PSO
2 0.9 0.17 7.9 3.5788 0033 0.004423 0.2078594 8.54681 3.96
3 0 00. 8. 4 5.
LENA
PEPPER
BABOON
HUNTER
MAP
CAMERAMAN
LIVINGROOM
HOUSE
AIRPLANE
0.0390.1100.4155 55558.35948594.40312969
4 0.1810 0.2594 2.3601 3.0640 9.1719 9.5156 4.7500 5.6094
5 0.2181 0.3043 4.5341 5.7362 9.4063 10.1250 5.2031 5.8938
2 0.0012 0.0031 0.0956 0.1455 7.1358 8.6492 3.4010 3.8569
3 0.0764 0.1750 0.1629 0.2891 7.6250 9.1056 4.3125 4.9787
4 0.1080 0.2707 2.1102 3.9721 8.1254 9.6406 4.6719 5.5156
5 0.1758 0.3048 3.2057 4.9999 8.4844 9.9688 4.8125 5.9844
2 0.0077 0.0567 0.1040 0.2224 8.0016 8.3563 3.8469 4.3969
3 0.0816 0.1580 0.5720 1.5317 8.7188 9.3750 4.3125 4.7969
4 0.0853 0.1765 2.1501 3.0653 9.1084 9.6750 4.9063 5.6094
5 0.1899 0.2775 3.4447 4.6721 9.7813 10.1875 5.3281 6.0109
2 0.0068 0.0148 0.2282 0.3283 8.000 8.6406 3.8438 4.4063
3 0.0936 0.1741 0.8203 1.8080 8.7031 9.9844 4.4844 4.8625
4 0.1560 0.2192 2.9836 6.3644 9.0313 9.6219 4.8125 5.3906
5 0.2720 0.3466 7.3030 11.1247 10.1406 10.6094 5.3031 6.1563
2 0.0023 0.0030 1.2241 1.8856 6.8906 7.4625 3.6094 4.2000
3 0.1153 0.1226 1.2298 2.1368 7.1563 7.6563 4.4219 4.9688
4 0.1366 0.1849 2.2333 4.5790 8.1250 8.9094 4.8750 5.5156
5 0.1521 0.1901 3.4511 6.3580 8.3594 9.7969 5.7500 6.4188
2 0.1001 0.1270 0.0908 0.3812 8.4844 9.2500 3.4844 3.9531
3 0.1107 0.2136 6.3502 9.4711 9.0625 9.7000 4.1250 4.8125
4 0.2005 0.2857 2.4498 4.5059 9.1250 9.9844 4.7406 5.2500
5 0.2734 0.3528 8.9650 11.0079 10.1094 10.9688 5.2656 6.0025
2 0.0022 0.0039 0.2637 0.5425 7.5844 8.2156 3.3281 3.7656
3 0.0718 0.1364 1.0446 2.4428 8.7188 9.6250 4.0469 4.9531
4 0.2286 0.3220 2.0787 3.0313 9.1001 9.7656 4.5000 5.1056
5 0.2619 0.3805 2.2655 4.3189 10.1719 10.5631 5.7969 6.6094
2 0.0224 0.0637 0.8001 1.7181 7.9063 8.3656 3.6252 4.4313
3 0.0805 0.1549 3.1018 6.2939 8.2626 9.2500 4.2969 4.9844
4 0.1324 0.2555 3.7038 8.2156 8.8438 9.5938 4.6094 5.3750
5 0.1824 0.2696 6.5478 9.9390 9.6406 10.0938 5.7344 6.6963
2 0.0106 0.0305 1.1731 2.7001 7.9844 8.7188 3.4688 4.0000
3 0.1248 0.1958 2.5107 5.0948 8.9688 10.4844 4.5938 5.1875
4 0.1424 0.3011 3.4728 7.0157 9.2031 9.9531 4.7969 5.3594
5 0.2760 0.3369 4.7571 8.6500 9.9688 10.4031 5.0781 5.8125
2 0.0025 0.0872 1.6744 2.3493 7.7188 8.4906 3.5313 3.9219
3 0.1880 0.2021 2.2356 3.4016 8.5469 9.4656 4.1875 4.9531
4 0.2473 0.2596 4.2227 5.2383 9.0000 9.8659 4.8281 5.5156
BUTTERFLY
5 0.2821 0.3977 5.1212 6.2719 9.3813 10.2469 5.4594 6.1313

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 137
(a) (a’) (a’’)
(b) (b’) (b’’)
Figure 3. Thresholded images obtainedd ((a), (b) represen-level thresholding, (a’), (b’) represents
4-level thresholdin
rm optimization (PSO) based
segmentation. In order to verify the efficiency and effec-
tiveness of the proposed PSO approach, ten standard test
ated. The performance of this ap-
mpared with the GA method, and it is
cessing, Vol. 58, No. 3, 1996, pp. 246-261.
[2] P. K. Sahoo, Song, “A Survey of
Thresholding Vision, Graphics
by Otsu-PSO methots 3
g, (a’’), (b’’) represents 5-level thresholding)
the objective function to decide whether the number of
hresholds has reached the optimal value or not. The
multilevel thresholding has been presented for image
t
higher value of the objective function results in better
segmentation.
For a visual interpretation of the segmentation results,
the segmented lena and cameraman images for both Ka-
pu
images are investig
proach has been co
found that PSO outperforms GA approach in terms of
solution quality, convergence and robustness. Compared
with all the cases, the Kapur-PSO gives lower standard
deviation value. Even though the Kapur-PSO gives lower
standard deviation, the Otsu-PSO method converges
quickly than the Kapur method. Hence, the Otsu-PSO
approach is an efficient tool for finding optimized thre-
shold values.
REFERENCES
[1] J. K. Udupa and S. Samarasekera, “Fuzzy Connectedness
and Object Definition: Theory, Algorithms and Applica-
Image Segmentation,” Graphical Models and
r-PSO and Otsu-PSO with m = 3, 4 and 5 are pre-
sented in Figures 2 and 3 respectively. It can be easily
seen that the quality of segmentation is better, in each
case, when m = 5 is chosen.
The standard deviation values and computation time
obtained from Kapur and Otsu based evolutionary algo-
rithms are given in Tabl e 5. The higher value of standard
deviation shows that the results of experiment are unsta-
ble. From the tables, it is seen that the PSO method is
more stable than the GA method. It is also observed
from the table that, even though the Kapur-based method
gives lower standard deviation than the Otsu’s method,
the computation time of Kapur based PSO is higher than
the Otsu based PSO.
6. Conclusions
In this paper, particle swa
tions in
Image Pro
. Soltani and A. K. C. W
Techniques,” Computer
and Image Processing, Vol. 41, No. 2, 1998, pp. 233-260.
[3] N. P. Pal and S. K. Pal, “A Review on Image Segmenta-

A New Multilevel Thresholding Method Using Swarm Intelligence Algorithm for Image Segmentation 138
tion Techniques,” Pattern Recognition, Vol. 26, No. 9,
1993, pp. 1277-1294.
[4] M. Sezgin and B. Sankar, “Survey over Image Thresh-
olding Techniques and Quantitative Performance Evalua-
tion,” Journal of Electronic Imaging, Vol. 13, No. 1,
2004, pp. 146-165.
[5] S. U. Lee, S. Y. Chung and R. H. Park, “A Comparative
Performance Study of Several Global Thresholding
hold Selection Method from Gray
ecognition Letters, Vol. 28, No. 7, 2007, pp
ransac-
r Gray-Level Picture Thresholding Using the
, Graphics and Image Processing, Vol. 16,
5, pp.49-56.
m Error Thresh-
“A Comparison of
. 17, No. 5, 2001, pp.
n and Applications, Vol. 13, No. 5-6, 2003, pp.
o. 3, 1997, pp. 305-313.
ert Systems with
. 7,
95.
ernational Journal of Hybrid In-
th, Vol. 4, 1995, pp. 1942-1948.
o. 1, 2008, pp.
Image and Vision Computing, Vol. 26, No. 8,
Techniques for Segmentation,” Computer Vision, Graph-
ics and Image Processing, Vol. 52, No. 2, 1990, pp.
171-190.
[6] N. Otsu, “A Thres- 254
Level Histograms,” IEEE Transaction on Systems, Man
and Cybernetics, Vol. 9, No. 1, 1979, pp. 62-66.
[7] W. Tao, H. Jin and L. Liu, “Object Segmentation Using
Ant Colony Optimization Algorithm and Fuzzy Entropy,”
Pattern R. [2
788-796.
[8] O. J. Tobias and R. Seara, “Image Segmentation by His-
togram Thresholding Using Fuzzy Sets,” IEEE T
tion on Image Processing, Vol. 11, No. 12, 2002, pp.
1457-1465.
[9] J. N. Kapur, P. K. Sahoo and A. K. C. Wong, “A New
Method fo
Entropy of The Histogram,” Computer Vision, Graphics
and Image Processing, Vol. 29, No. 3, 1985, pp. 273-285.
[10] T. Pun, “Entropy Thresholding: A New Approach,” Com-
puter Vision
No. 3, 1981, pp. 210-239.
[11] A. D. Brink, “Minimum Spatial Entropy Threshold Selec-
tion,” IEEE Proceedings, Vision Image and Signal Proc-
essing, Vol. 142, No. 3, 1995, pp. 128-132.
[12] X. Li, Z. Zhao and H. D. Cheng, “Fuzzy Entropy Thresh-
old Approach to Breast Cancer Detection,” Information
Sciences, Vol. 4, No. 1, 199
[13] L. K. Huang and M. J. Wang, “Image Thresholding by
Minimizing the Measure of Fuzziness,” Pattern Recogni-
tion, Vol. 28, No. 1, 1995, pp. 41-51.
[14] J. Kittler and J. Illingworth, “Minimum Error Threshold-
ing,” Pattern Recognition, Vol. 19, No. 1, 1986, pp. 41-47.
[15] Q. Ye and P. Danielsson, “On Minimu
olding and its Implementation,” Pattern Recognition Let-
ters, Vol. 7, No. 4, 1988, pp. 201-206.
[16] U. Gonzales-Baron and F. Butler,
789-
Seven Thresholding Techniques with the K-Means Clus-
tering Algorithm for Measurement of Bread-Crumb Fea-
tures by Digital Image Analysis,” Journal of Food Engi-
neering, Vol. 74, No. 2, 2006, pp. 268-278.
[17] P. Y. Yin and L. H. Chen, “A Fast Iterative Scheme For
Multilevel Thresholding Methods,” Signal Processing,
Vol. 60, No. 3, 1997, pp. 305-313.
[18] P. S. T. Liao, S. Chen and P. C. Chung, “A Fast Algo-
rithm for Multilevel Thresholding,” Journal of Informa-
tion Science and Engineering, Vol
713-727.
[19] K. C. Lin, “Fast Image Thresholding by Finding Zero(S)
of the First Derivative of between Class Variance,” Ma-
chine Visio
-262.
[20] P.-Y. Yin and L.-H. Chen, “A Fast Iterative Scheme for
Multilevel Thresholding Methods,” Signal Processing,
Vol. 60, N
1] E. Cuevas, D. Zaldivar and M. Perez-Cisneros, “A Novel
Multi-Threshold Segmentation Approach Based on Dif-
ferential Evolution Optimization,” Exp
Applications, Vol. 37, No. 7, 2010, pp. 5265-5271.
[22] W. B. Tao, H. Jin and L. M. Liu, “Object Segmentation
Using Ant Colony Optimization Algorithm and Fuzzy
Entropy,” Pattern Recognition Letters, Vol. 28, No
2008, pp. 788-796.
[23] P. Y. Yin, “A Fast Scheme for Optimal Thresholding
Using Genetic Algorithms,” Signal Processing, Vol. 72,
No. 2, 1999, pp. 85-
[24] C. C. Lai and D. C. Tseng, “A Hybrid Approach Using
Gaussian Smoothing and Genetic Algorithm for Multi-
level Thresholding,” Int
telligent Systems, Vol. 1, No. 3, 2004, pp. 143-152.
[25] D. B. Fogel, “Evolutionary Computation: Toward a New
Philosophy of Machine Intelligence,” 2nd Edition, IEEE
Press, Piscataway, 2000.
[26] J. Kennedy and R. Eberhart, “Particle Swarm Optimiza-
tion,” Proceedings of the IEEE Conference on Neural
Networks—ICNN’95, Per
[27] Y.-T. Kao, E. Zahara and I-W. Kao, “A Hybridized Ap-
proach to Data Clustering,” Expert Systems with Applica-
tions, Vol. 34, No. 3, 2008, pp. 1754-1762.
[28] Z.-J. Lee, S.-W. Lin, S.-F. Su and C.-Y. Lin, “A Hybrid
Watermarking Technique Applied to Digital Images,”
Expert Systems with Applications, Vol. 8, N
808.
[29] C.-C. Tseng, J.-G. Hsieh and J.-H. Jeng, “Fractal Image
Compression Using Visual-Based Particle Swarm Opti-
mization,”
2008, pp. 1154-1162.