Journal of Modern Physics, 2012, 3, 1835-1839
http://dx.doi.org/10.4236/jmp.2012.312229 Published Online December 2012 (http://www.SciRP.org/journal/jmp)
Branching Ratios from H→γγ and H→Zγ with
a 125 GeV Higgs Boson
Alejandro Gutiérrez-Rodríguez1, María de los Ángeles Hernández-Ruíz2,
Polet Castañeda-Almanza1, Alejandro González-Sánchez1
1Facultad de Física, Universidad Autónoma de Zacatecas, Zacatecas, México
2Unidad Académica de Ciencias Químicas, Universidad Autónoma de Zacatecas, Zacatecas, México
Received July 1, 2012; revised October 19, 2012; accepted November 1, 2012
ABSTRACT
Motivated by the recent result reported from LHC on the di-photon search from the Standard Model (SM) Higgs boson,
we obtain limits on the anomalous couplings Hγγ and HZγ. We also perform a calculation at tree level of the decay
widths as well as of the branching ratios for the reactions H → γγ and H → Zγ in the context of effective lagrangian for
Higgs boson masses 115 ≤ MH ≤ 130 GeV. We find that the decay widths and branching ratios from these reactions en-
hanced significantly due to the anomalous Hγγ and HZ γ vertex, which would lead to measurable effects in Higgs signals
at the LHC. Moreover, our results complement other studies on the channels H → γγ and H → Zγ.
Keywords: Standard Model Higgs Boson; Models beyond the Standard Model
1. Introduction
Recently, the Large Hadron Collider (LHC) of the Euro-
pean Center for Nuclear Research (CERN), has collected
valuable data on the Higgs boson of the standard model
of electroweak and strong interactions. Both ATLAS and
CMS collaborations at LHC have performed a combined
search [1] on Higgs boson. The main production chan-
nels used by both collaborations are: H → γγ, H → ZZ*
→ 4l and H → WW* → 2ν2l. These experiments have
reported an excess of events in channel research for an
invariant mass m ≈ 125 GeV with a confidence level of
2σ to 3σ, which could be the first evidence of existence
of the Higgs boson.
In the Standard Model (SM) of electroweak interac-
tions there are no couplings at the tree level among three
neutral bosons such as Hγγ and HZγ. These couplings
only appear at the one-loop level through fermion and
charged vector bosons [2-4]. In the SM it is dominated
by W gauge boson and top quark loops and the branching
ratio for the decay modes H → γγ and H → Zγ reaches its
maximumvalue of order 10–3 for an intermediate mass
Higgs boson (115 ≤ MH ≤ 140 GeV) [4]. The decay H →
γγ is induced at one loop in the context of the standard
model, and this channel is one of the main means of
production in the next generation of linear colliders. This
decay is also attractive in the LHC because it does not
suffer from the uncertainty caused by the reconstruction
of the jets, as in other decay channels. The study of these
vertex H → γγ and H → Zγ has attracted much attention
because their strength can be sensitive to scales beyond
the SM. The interest in this type of couplings thus lies in
the additional contributions that may appear in exten-
sions of the SM, for example, new charged scalar and
vector bosons in Left-Right (L-R) symmetric gauge
models [5], or Two Higgs Doublet Models (THDM)
[6,7], as well as charginos and neutralinos in the Minimal
Supersymmetric Standard Model (MSSM) [6,7]. The SM
and LR symmetric models predict an anomalous HZγ
vertex of order 10–4 [2,4], the MSSM may induce a sup-
pression effect [6,7] but an effective lagrangian approach
leaves room for an enhancement effect [6,8-10]. These
models arise as an interesting alternative to analyze the
couplings at the tree level among three neutral bosons
such as Hγγ and HZγ. Sukanta Dutta, Kaoru Hagiwara
and Yu Matsumoto [10] have proposed a model based on
the effective lagrangian of the Higgs and the gauge bos-
ons with operators up to mass dimension six. Detailed
discussions on effective lagrangian can be found in the
literature [6-9,11].
The sensitivity to the Hγγ and HZγ vertex has been
studied in processes such as e–γ → e
–H, e+e– → Hγ
[4,9,12] and e+e– → τ+τ–γ [13], rare Z and H decays
[14-16], pp collisions via the basic interaction qq → qqH
[16] and the annihilation process e+e– → HZ [9,17,18].
Our aim in the present paper is to analyze the reactions
H → γγ and H → Zγ in the framework of the effective
lagrangian [10]. In this paper, we take advantage of this
C
opyright © 2012 SciRes. JMP

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1836
formalism with anomalous couplings Hγγ and HZγ to
obtain limits on 1,2 1,2
Z
hh


 
2H
p Hp

. We also perform a calculation
at tree level on the decay widths and branching ratios
from reactions H → γγ and H → Zγ.
The paper is organized as follows: in Section 2 we
present the calculation of the reactions H → γγ and H →
Zγ and in Section 3 we present our results and conclu-
sions.
2. Decay Widths and Branching Ratios from
H → γγ and H → Zγ
In this section we present the decay widths of the reac-
tions H → γγ and H → Zγ in the context of the effective
lagrangian given in Ref. [10].
2.1. Decay Width of H → γγ
We calculate the decay width for the reaction H → γγ
using the terms that describe the HVV couplings in the
effective lagrangian given in Equation (11) of Ref. [10].
From this lagrangian the Feynman rule for

11 2
–Vp V

vertex is given by [10]

12
12
12
2
,,
HV V
H
VV
ZZ
ppp
h
gM h g






12
2
121
2,
VV
Z
p p
M
 



(1)
where MZ is the Z boson mass, cos
z
W
ge

 and p1 +
p2 + pH = 0 as shown in Figure 1 of Ref. [10]. In Equa-
tion (1) V1 and V2 can be


 
or .W W


12 12
,
VV
i
hpp
12 ZZ ,Z,Z ,VVW W



The coefficients are


11
2
212
,2
pp
hp p
hppp c

22 2
12 2
2
2
,,
,
H
Z
M
c
M







(2)
for the Hγγ couplings,



22 2
12
112 2
22
12
2
22 2
12
112 2
22
12
2
212 212
,
,
,,
ZH
Z
H
Z
ZH
Z
H
Z
ZZ
ppM
hpp M
ppM
M
ppM
hpp M
ppM
M
hpp hpp









 



2
2
3
2
2
3
2 3
,
,
2,
Z
Z
Z
Z
ZZ
c
c
c
c
c c






12
1
VV
h12
2
VV
h
(3)
for the HZγ couplings. A interesting characteristic of this
model is that the coefficients and are the
only additional parameters.
The respective transition amplitude for the reaction H
→ γγ is thus given by



1211 22
,,,, ,
H
H
MH
ppp pp
 



 

 (4)
where εµ(p1, λ1) and εν(p2, λ2) are the polarization vectors
of the photons and Γµν(pH, p1, p2) is given in Equation (1).
While the square of the transition amplitude for the reac-
tion H → γγ is
 
4
22
222
12
4
4,
2
H
ZZ
Z
M
MgM hh
M
 










(5)
The decay width in the context of effective lagrangian
is given by
 
22 4
22
12
4
4.
16 π2
ZZ H
HZ
gM M
Hhh
MM
 



  (6)




In the standard model at tree level, the decay width is
zero. Evaluating the limit when the coefficients


0hh
 
h
12 the terms that depend on 1


h and 2


in (6) are zero and the results of the SM are recovered.
2.2. Decay Width of H → Zγ
Following a similar procedure as in the case of the decay
H → γγ, the expression for the square of the amplitude of
transition of H → Zγ is



2
22
2 2222 2
14
3,
4
Z
Z
ZZH Z
Z
h
MgM hMM
M














 (7)
while the corresponding decay width is given by


  
2
222 2
22
22
32
12
12 .
64π
ZZH Z
HZ
HZ
ZZ
HZ
gMM M
MM
MM
hh

  









(8)





Using the fact that for on-shell particles, only one of
the form factors given in Equation (1) contributes to the
decay width [6], Equation (8) can be expressed by


22
1
3
22 2
8π.
Z Z
H
ZH Z
g
HZ h
M
MM M

   (9)
3. Results and Conclusions
For the numerical computation of the reactions H → γγ
and H → Zγ in the context of effective lagrangian and
anomalous couplings Hγγ and HZγ, we have adopted the
following parameters: the angle of Weinber sin2θW =
0.232, the mass (mb = 4.5 GeV) of the bottom quark, the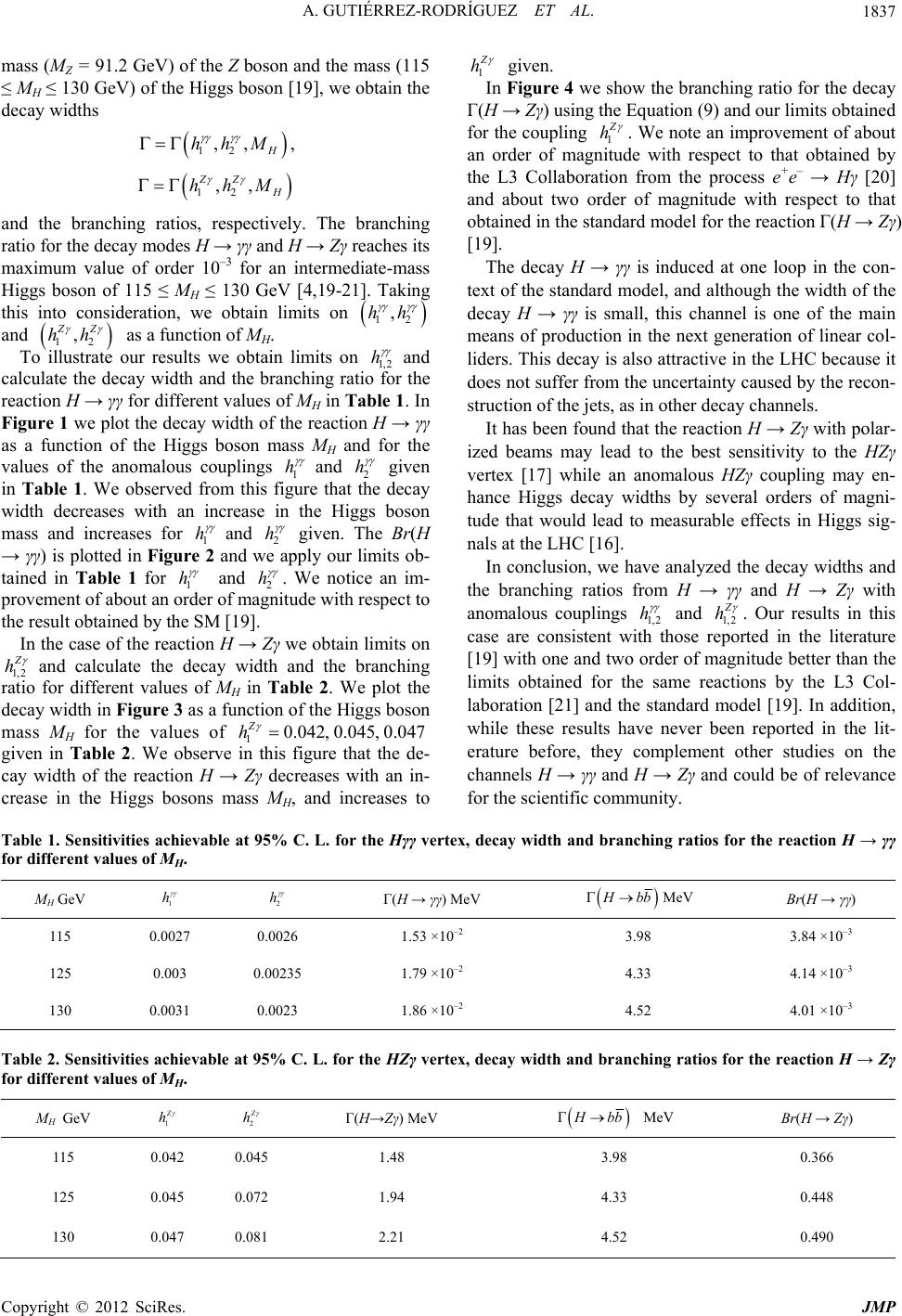

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1837

12
,,
mass (MZ = 91.2 GeV) of the Z boson and the mass (115
≤ MH ≤ 130 GeV) of the Higgs boson [19], we obtain the
decay widths
H
hhM
 

12
,,
ZZ
H
hhM

 ,

and the branching ratios, respectively. The branching
ratio for the decay modes H → γγ and H → Zγ reaches its
maximum value of order 10–3 for an intermediate-mass
Higgs boson of 115 ≤ MH ≤ 130 GeV [4,19-21]. Taking
this into consideration, we obtain limits on


12
,hh



,
ZZ
hh and 12


h
as a function of MH.
To illustrate our results we obtain limits on 1,2


and
calculate the decay width and the branching ratio for the
reaction H → γγ for different values of MH in Table 1. In
Figure 1 we plot the decay width of the reaction H → γγ
as a function of the Higgs boson mass MH and for the
values of the anomalous couplings 1 h


h
and 2


given
in Table 1. We observed from this figure that the decay
width decreases with an increase in the Higgs boson
mass and increases for 1 h


and 2
h


given. The Br(H
→ γγ) is plotted in Figure 2 and we apply our limits ob-
tained in Table 1 for 1 h


and 2 h


. We notice an im-
provement of about an order of magnitude with respect to
the result obtained by the SM [19].
In the case of the reaction H → Zγ we obtain limits on
1,2
Z
h

and calculate the decay width and the branching
ratio for different values of MH in Table 2. We plot the
decay width in Figure 3 as a function of the Higgs boson
mass MH for the values of 1
given in Table 2. We observe in this figure that the de-
cay width of the reaction H → Zγ decreases with an in-
crease in the Higgs bosons mass MH, and increases to
0.042,
Z
h

0.045, 0.047
1
Z

h given.
In Figure 4 we show the branching ratio for the decay
Γ(H → Zγ) using the Equation (9) and our limits obtained
for the coupling 1
Z
h

. We note an improvement of about
an order of magnitude with respect to that obtained by
the L3 Collaboration from the process e+e– → Hγ [20]
and about two order of magnitude with respect to that
obtained in the standard model for the reaction Γ(H → Zγ)
[19].
The decay H → γγ is induced at one loop in the con-
text of the standard model, and although the width of the
decay H → γγ is small, this channel is one of the main
means of production in the next generation of linear col-
liders. This decay is also attractive in the LHC because it
does not suffer from the uncertainty caused by the recon-
struction of the jets, as in other decay channels.
It has been found that the reaction H → Zγ with polar-
ized beams may lead to the best sensitivity to the HZγ
vertex [17] while an anomalous HZγ coupling may en-
hance Higgs decay widths by several orders of magni-
tude that would lead to measurable effects in Higgs sig-
nals at the LHC [16].
In conclusion, we have analyzed the decay widths and
the branching ratios from H → γγ and H → Zγ with
anomalous couplings 1,2
h


and 1,2
Z
h

. Our results in this
case are consistent with those reported in the literature
[19] with one and two order of magnitude better than the
limits obtained for the same reactions by the L3 Col-
laboration [21] and the standard model [19]. In addition,
while these results have never been reported in the lit-
erature before, they complement other studies on the
channels H → γγ and H → Zγ and could be of relevance
for the scientific community.
Table 1. Sensitivities achievable at 95% C. L. for the Hγγ vertex, decay width and branching ratios for the reaction H → γγ
for different values of MH.

MH GeV 1
h

2 h

Γ(H → γγ) MeV

H
bbMeV Br(H → γγ)
1.53 ×10–2 3.84 ×10–3 115 0.0027 0.0026 3.98
1.79 ×10–2 125 0.003 0.00235 4.33 4.14 ×10–3
1.86 ×10–2 4.52 4.01 ×10–3 130 0.0031 0.0023
Table 2. Sensitivities achievable at 95% C. L. for the HZγ vertex, decay width and branching ratios for the reaction H → Zγ
for different values of MH.

MH GeV 1
Z
h

2
Z
h

Γ(H→Zγ) MeV

MeV Br(H → Zγ)
H
bb
115 0.042 0.045 1.48 3.98 0.366
125 0.045 0.072 1.94 4.33 0.448
130 0.047 0.081 2.21 4.52 0.490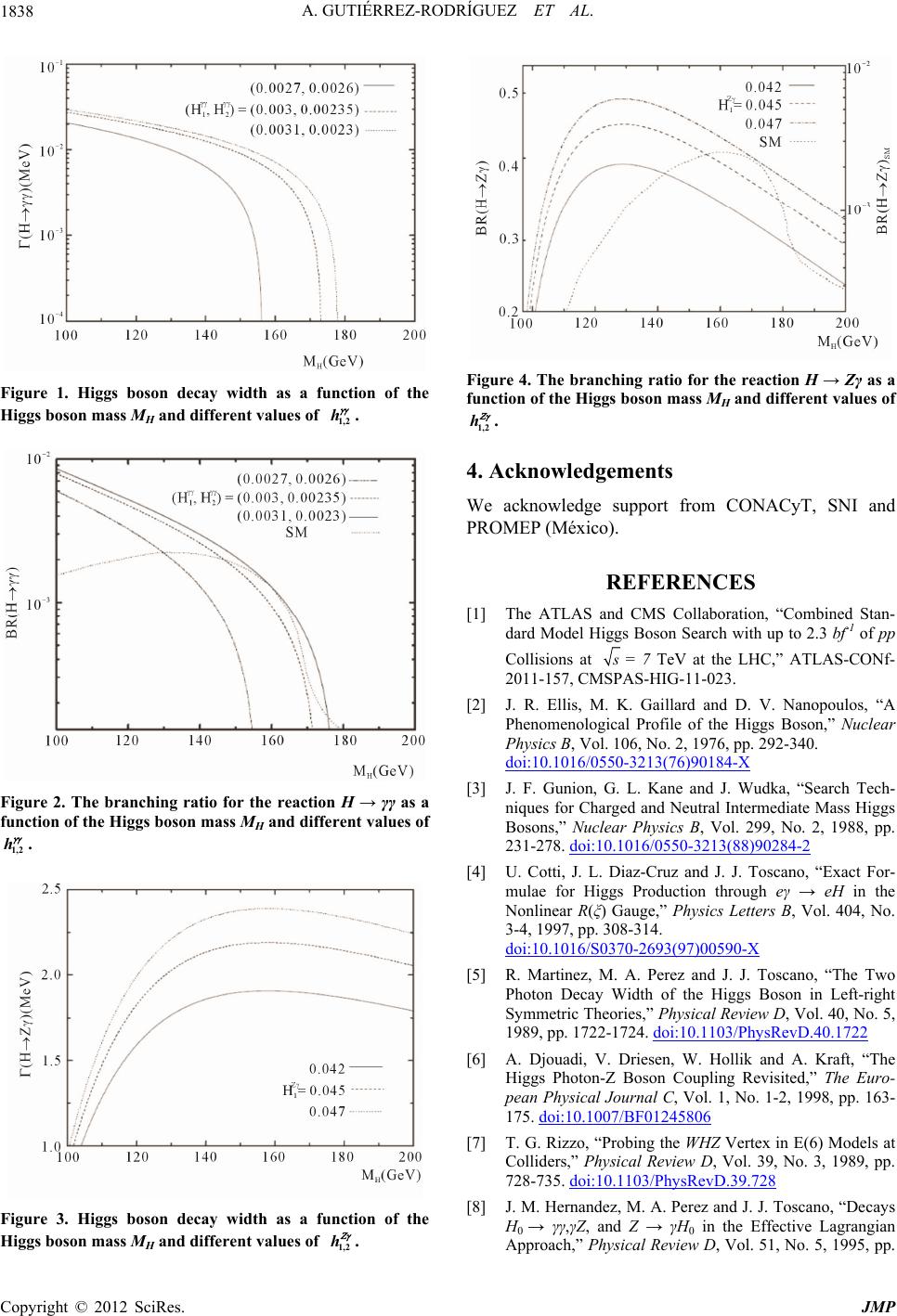

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1838
Figure 1. Higgs boson decay width as a function of the
Higgs boson mass MH and different values of h1,2

.
Figure 2. The branching ratio for the reaction H → γγ as a
function of the Higgs boson mass MH and different values of
h1,2

.
Figure 3. Higgs boson decay width as a function of the
Higgs boson mass MH and different values of
Figure 4. The branching ratio for the reaction H → Zγ as a
function of the Higgs boson mass MH and different values of
h1,2

.
4. Acknowledgements
We acknowledge support from CONACyT, SNI and
PROMEP (México).
REFERENCES
[1] The ATLAS and CMS Collaboration, “Combined Stan-
dard Model Higgs Boson Search with up to 2.3 bf-1 of pp
Collisions at
s
= 7 TeV at the LHC,” ATLAS-CONf-
2011-157, CMSPAS-HIG-11-023.
[2] J. R. Ellis, M. K. Gaillard and D. V. Nanopoulos, “A
Phenomenological Profile of the Higgs Boson,” Nuclear
Physics B, Vol. 106, No. 2, 1976, pp. 292-340.
doi:10.1016/0550-3213(76)90184-X
[3] J. F. Gunion, G. L. Kane and J. Wudka, “Search Tech-
niques for Charged and Neutral Intermediate Mass Higgs
Bosons,” Nuclear Physics B, Vol. 299, No. 2, 1988, pp.
231-278. doi:10.1016/0550-3213(88)90284-2
[4] U. Cotti, J. L. Diaz-Cruz and J. J. Toscano, “Exact For-
mulae for Higgs Production through eγ → eH in the
Nonlinear R(ξ) Gauge,” Physics Letters B, Vol. 404, No.
3-4, 1997, pp. 308-314.
doi:10.1016/S0370-2693(97)00590-X
[5] R. Martinez, M. A. Perez and J. J. Toscano, “The Two
Photon Decay Width of the Higgs Boson in Left-right
Symmetric Theories,” Physical Review D, Vol. 40, No. 5,
1989, pp. 1722-1724. doi:10.1103/PhysRevD.40.1722
[6] A. Djouadi, V. Driesen, W. Hollik and A. Kraft, “The
Higgs Photon-Z Boson Coupling Revisited,” The Euro-
pean Physical Journal C, Vol. 1, No. 1-2, 1998, pp. 163-
175. doi:10.1007/BF01245806
[7] T. G. Rizzo, “Probing the WHZ Vertex in E(6) Models at
Colliders,” Physical Review D, Vol. 39, No. 3, 1989, pp.
728-735. doi:10.1103/PhysRevD.39.728
[8] J. M. Hernandez, M. A. Perez and J. J. Toscano, “Decays
H0 → γγ,γZ, and Z → γH0 in the Effective Lagrangian
Approach,” Physical Review D, Vol. 51, No. 5, 1995, pp.
h1,2


.

A. GUTIÉRREZ-RODRÍGUEZ ET AL. 1839
2044-2048. doi:10.1103/PhysRevD.51.R2044
[9] K. Hagiwara and M. L. Stong, “Probing the Scalar Sector
in e+e− → ffH,” Zeitschrift fur Physik C, Vol. 62, 1994, pp.
99-108. doi:10.1007/BF01559529
[10] S. Dutta, K. Hagiwara and Y. Matsumoto, “Measuring the
Higgs-Vector Boson Couplings at Liner e+e− Collider,”
Physical Review D, Vol. 78, No. 11, 2008, Article ID:
115016. doi:10.1103/PhysRevD.78.115016
[11] J. de Blas Mateos, “Effective Lagrangian Descrition of
Physics beyond the Standard Model and Electroweak
Precision Tests,” Universidad de Granada, Granada, 2010.
[12] G. J. Gounaris, J. Layssac and F. M. Renard, “The Proc-
esses e-e+→γγ, Zγ, ZZ in SM and MSSM,” Physical Re-
view D, Vol. 67, No. 1, 2003, Article ID: 013012.
[13] A. Gutiérrez-Rodríguez, J. Montaño and M. A. Pérez,
“Bounds on Anomalous HZγ Vertex Arising from the
Process e+e−→τ+τ−γ,” Journal of Physics G: Nuclear and
Particle Physics, Vol. 38, No. 9, 2011, Article ID: 095003.
doi:10.1088/0954-3899/38/9/095003
[14] C.-S. Li, C.-F. Qiao and S.-H. Zhu, “Radiative Higgs Boson
Decays H → ffγ beyond the Standard Model,” Physical
Review D, Vol. 57, 1998, pp. 6928-6933.
doi:10.1103/PhysRevD.57.6928
[15] M. A. Perez, G. Tavares-Velasco and J. J. Toscano, “New
Physics Effects in Rare Z Decays,” International Journal
of Modern Physics A, Vol. 19, No. 2, 2004, pp. 159-178.
doi:10.1142/S0217751X04017100
[16] V. Hankele, G. Klamke, D. Zeppenfeld and T. Figy,
“Anomalous Higgs Boson Couplings in Vector Boson Fu-
sion at the CERN LHC,” Physical Review D, Vol. 74, No.
9, 2006, Article ID: 095001.
doi:10.1103/PhysRevD.74.095001
[17] S. D. Rindani and P. Sharma, “Angular Distributions as a
Probe of Anomalous ZZH and γZH Interactions at a Lin-
ear Collider with Polarized Beams,” Physical Review D,
Vol. 79, No. 7, 2009, Article ID: 075007.
doi:10.1103/PhysRevD.79.075007
[18] W. Kilian, M. Kramer and P. M. Zerwas, “Anomalous
Couplings in the Higgsstrahlung Process,” Physics Letters
B, Vol. 381, No. 1-3, 1996, pp. 243-247.
doi:10.1016/0370-2693(96)00537-0
[19] K. Nakamura, et al., “Particle Data Group,” Journal of
Physics G: Nuclear and Particle Physics, Vol. G37, 2010,
p. 1.
[20] K. Fujii, K. Ikematsu, S. Kanemura, Y. Kurihara, N. Maeda
and T. Takahashi, “Feasibility Study of Higgs Pair Crea-
tion in γγ Collider,” arXiv: 1008.0907 [hep-ph].
[21] P. Achard, et al., “Search for Anomalous Couplings in the
Higgs Sector at LEP,” Physics Letters B, Vol. 589, No.
3-4, 2004, pp. 89-102.
doi:10.1016/j.physletb.2004.03.048