Int. J. Communications, Network and System Sciences, 2010, 3, 679-688
doi:10.4236/ijcns.2010.38091 Published Online August 2010 (http://www.SciRP.org/journal/ijcns)
A New Scheduling Algorithm for Reducing Data
Aggregation Latency in Wireless Sensor Networks*
Meirui Ren1,2, Longjiang Guo1,2#, Jinbao Li1,2
1School of Computer Science and Technology, Heilongjiang University, Harbin, China
2Key Laboratory of Database and Parallel Computing of Heilongjiang Province, Harbin, China
Received April 20, 2010; revised June 21, 2010; accepted July 29, 2010
Abstract
Existing works on data aggregation in wireless sensor networks (WSNs) usually use a single channel which
results in a long latency due to high interference, especially in high-density networks. Therefore, data aggre-
gation is a fundamental yet time-consuming task in WSNs. We present an improved algorithm to reduce data
aggregation latency. Our algorithm has a latency bound of 16R + Δ – 11, where Δ is the maximum degree
and R is the network radius. We prove that our algorithm has smaller latency than the algorithm in [1]. The
simulation results show that our algorithm has much better performance in practice than previous works.
Keywords: Reducing Latency, Wireless Sensor Networks, Scheduling Algorithm
1. Introduction
A wireless sensor network (WSN) consists of sensor no-
des that are capable of sensing, processing, and transmit-
ting. Each node is responsible for covering a certain geo-
graphical area with the primary functions of monitoring
changes and reporting them using its radio transmitter to
the sink(base station) and in cooperation with other no-
des. Sensory data is sent to the sink in a multi-hop mode.
WSNs have no infrastructure and nodes are self-or-
ganized arbitrarily. WSNs have proven their success in a
various applications such as battlefield surveillance, traf-
fic monitoring and forest fire monitoring. In some appli-
cations, e.g. forest fire monitoring and aquiculture sur-
veillance, end users want to extract data aggregation in-
formation from WSNs with low latency.
However, WSNs usually use a single channel, which
results in a long latency due to high interference, especi-
ally in high-density networks. When two or more sensors
send data to a common neighbor at the same time, data
collision occurs at the common neighbor, preventing it
from successfully receiving any data. The data sent by a
sender should be received by a corresponding receiver
with no collisions. The receiver aggregates the received
data with its own data, and stores the aggregated data as
its new data. The time consumed by a single sending-re-
ceiving-aggregating-storing is normalized to one, and pa-
rallel sending-receivings are desirable for reducing net-
work delay.
In this paper, we focus on reducing the latency of data
aggregation by constructing a good schedule with low
latency. Minimum Data Aggregation Latency (MDAL) is
an important research problem. MDAL is defined as fol-
lows: Given a wireless senor network that consists of a
number of sensors and a sink, supposing each sensor has
a piece of data to be aggregated and transmitted to the
sink, the MDAL problem is to design a transmission
schedule of data aggregation for all sensors such that
there is no conflict between any two concurrent trans-
missions and the total number of timeslots for all data to
reach the sink is minimized.
*National Natural Science Foundation of China (NSFC) for Young Sch-
olar under grant No. 60803015; China Postdoctoral Science Foundation
under grant No. 20080430902; Science and Technology Innovation Re-
search Project of Harbin for Young Scholar under grant No. 2008RFQ-
XG107; Heilongjiang Postdoctoral Science Foundation under grant No.
LRB08-021; Science and Technology Key Research of Heilongjiang Ed-
ucational Committee under grant No.1154Z1001; Heilongjiang Univer-
sity Fundation for Distinguished Young Scholars; The National Natural
Science Foundation of China (No.61070193); the Key Scientific and
Technological Research Project of Heilongjiang Province of China
(
No.GC09A109
)
.
Extensive research has been conducted on the MDAL
problem, such as [1,2]. Chen et al. [2] prove that the MD-
AL problem is NP-hard. They designed a (Δ – 1)-appro-
ximation algorithm named SDA (Shortest Data Aggrega-
tion) based on Shortest Path Tree for data aggregation
with a latency bound of (Δ – 1)·R, where Δ is the maxi-
mum degree and R is the network radius. Huang et al. [1]
proposed an algorithm based on Maximal Independent Set

680 M. R. REN ET AL.
which has a latency bound of 23R + Δ – 18. Here Δ con-
tributes to an additive factor instead of a multiplicative one.
The algorithm is a nearly constant approximation and it
has a significantly less latency bound than earlier algo-
rithms especially when Δ is large. In this paper, we present
an algorithm relying on reducing the number of blue nodes
and finding maximal non-conflicting transmission sched-
ule sets which has a latency bound of 16R + Δ – 11. Our
algorithm is also a nearly constant approximation and it
has a significantly less latency bound than the existing best
known algorithm in [1] when R is large.
The remainder of this paper is organized as follows.
The formalized MDAL problem and all related work are
presented in Section 2. In Section 3, we propose our alg-
orithm and give details of analysis on performance. In
Section 4, we evaluate the average performance of the
proposed algorithm through simulations and compare it
with the algorithm in [1]. Section 5 concludes this paper.
2. Preliminaries
In this section, we first present some assumptions and
formalize the MDAL problem, and then we discuss all
related work in details.
2.1. Problem Description
We consider a wireless sensor network consisting of sta-
tionary nodes along with one sink node distributed over
an Euclidean plane. All the sensor nodes are homogene-
ous. Each sensor node is equipped with a RF transceiver
that can be used to send or receive data. We assume that
each sensor node has omni-directional antenna and the
transmission coverage of any sensor node is a circle with
unit radius centered at the sensor.
We assume that each sensor knows its geometric posi-
tion in the network. The sink has global knowledge of all
the sensors’ IDs and positions. Transmission is determin-
istic and proceeds in synchronous time rounds controlled
by a global clock.
In each time round, any node cannot send and receive
data simultaneously, i.e. any node either sends data or
receives data in a round.
Definition 1 [Neighbor Set] For a sensor node u, if
there exists another sensor node v such that v lies in u’s
transmission area, then v is called u’s neighbor. All of
u’s neighbors form a set, which is called u’s Neighbor
Set, denoted by Neighbor(u).
Data sent by any sender simultaneously reaches all the
nodes in its neighbor set.
Definition 2 [Transmission Schedule] u → v is call- ed
a Transmission Schedule, where u is called sender, v is
called a receiver. u → v denotes that u transmits data to v.
If two or more nodes are sending in the same round
and there exists a node u in their overlapped transmission
area, then u cannot successfully receive any data since all
transmissions are interfering with each other. This situa-
tion is called a collision. For example, in Figure 1(a),
there are two ongoing transmission schedules u → v and
x → v in the same round. v will not receive anything. In
Figure 1(b), there are two ongoing transmission sched-
ules u → v and x → y in the same round. v is in x’s
transmission range, therefore v will not receive anything.
Definition 3 [Conflicting Transmission Schedules] u
→ v and x → y are called Conflicting Transmission Sc-
hedules if and only if v  Neighbor(x) or y  Neigh-
bor(u).
The main task of a sensor is to collect data and forw-
ard aggregated data to the sink, and data can be “aggreg-
ated” all the way to the sink. In other words, if a node
has received one packet from its neighbor before its
scheduled transmission time round, then it can merge this
packet with its own data packet and simply waits to send
this merged packet later. The situation where packets
cannot be merged does exist, and it is called data collec-
tion. In this paper we only focus on data aggregation
meaning that data can be merged all the way to the sink.
For simplicity, a wireless sensor network with sink
node s can be represented as a graph G = (V, E), where V
denotes all the sensor nodes in the network and s  V,
An edge (u, v)  E indicates that u lies in v’s transmis-
sion range and v lies in u’s transmission range.
A data aggregation schedule is a sequence of transmi-
ssion schedule sets {S1, S2, …, Sl}, where Si (i = 1,2,…l)
is a transmission schedule set satisfying the following
conditions:
1) Any two transmission schedules u → v, x → y in Si
(i = 1,2,…l) are non-conflicting transmission schedules,
i.e. v  Neighbor(x) and y  Neighbor(u).
2)i  j, Sender (Si) ∩ Sender (Sj) = , where Sender
(Si) denotes the sender set of transmission schedules in
Si.
3) .
1
() {}
l
i
i
Sender SVs



l is called the data aggregation latency.
The MDAL problem is defined as follows. Given a
graph G = (V, E) and the sink node s  V, find a data
aggregation schedule with the minimum latency.
u
v
xu
v
x
y
(a) (b)
Figure 1. Two types of collisions.

M. R. REN ET AL.
681
2.2. Related Work
Extensive research has been conducted on data aggrega-
tion. One category of existing works focuses on how to
design an energy efficient data aggregation algorithm. Th-
ese works of data aggregation focus on energy efficiency.
Data aggregation is also called convergecast. Convergec-
ast is about a sensor network with a sink such that all se-
nsor nodes collect data and report to the sink through mu-
lti-hop communications. Annamalai et al. [3] designed a
heuristic algorithm for both broadcast and convergecast.
The convergecast tree constructed in their algorithm can
be used for broadcast as well. Upadhyayula et al. [4] de-
signed another heuristic algorithm for convergecast, aim-
ing at reducing energy consumption and latency. These
two works mentioned above both proposed heuristic app-
roaches and used simulations to verify their results wit-
hout giving theoretical analysis. In our work, we verified
our results through both simulations and theoretical ana-
lysis.
Another category focuses on how to design a conflict-
free scheduling. A distributed cross-layer scheduling pro-
tocol for data aggregation was proposed in [5], in which
each node negotiates with its parent to decide its times-
lots for transmission and constructs a schedule for its qu-
ery processing. Chipara et al. [6] developed a dynamic
scheduling scheme supporting different kinds of aggreg-
ation queries, assuming that an aggregation tree has alr-
eady been constructed. Yu et al. [7] studied the energy-
latency tradeoff of scheduling for data aggregation. Pract-
ical issues of data aggregation, especially about the MAC
layer, have also been studied in the literature. Huang and
Zhang [8] studied packet loss and focused on reliability
issues in data aggregation. Zhang et al. [9] addressed the
issue of bursty convergecast in real-time applications.
The high-volume burst traffic often arises in event-driven
applications. These applications require for reliable and
real-time packet delivery to the sink. The large number
of packets generated within a short period leads to high
degree of channel contention and thus a high probability
of packet collision. Zhang et al. focused on improving
channel utilization and reducing retransmission incurred
by channel contention. Krishnamachari et al. [10] studied
data aggregation from another aspect. They considered
the case where there is a subset of nodes whose data need
to be sent to the sink and regard aggregating these data as
a way to save energy. Intanagonwiwat et al., in a short
paper [11], evaluated the impact of greedy aggregation to
increase the amount of path sharing and reduce energy
consumption. All the above works aimed at minimizing
the overall energy consumption of sensors subject to the
latency constraint.
The most relevant works of the MDAL problem are on
theoretical side. Kesselman and Kowalski [12] designed
a randomized, distributed algorithm with latency O(log
n). In their model, it is assumed each node can vary its
transmission range to reduce links. Chen et al. [2] de-
signed a (Δ – 1)-approximation algorithm called SDA for
data aggregation, which has a latency bound of (Δ – 1)·R,
where Δ is the maximum degree of the network and R is
the network radius. They also proved that the minimum
data aggregation time problem is NP-hard. Huang et al.
[1] designed an algorithm based on maximal independent
sets which has a latency bound of 23R + Δ – 18. They
reduced the data aggregation latency from a multiplica-
tive factor of Δ to additive factor. Their algorithm is
nearly constant and it has a significantly less latency
bound than the previous algorithms when Δ is large.
In this paper, we present an algorithm based on reduc-
ing the number of blue nodes and maximal non-confli-
cting transmission schedule sets which has a latency
bound of 16R + Δ – 11. Our algorithm is also nearly con-
stant and it has a significantly less latency bound than the
previous algorithms.
3. Our Data Aggregation Algorithm
In this section, we present our approximation algorithm.
Our algorithm has a data aggregation latency of 16R + Δ
– 11, where R is the network radius and Δ is the maxi-
mum degree of the network. This result is better than the
currently best known algorithm [1] whose latency is 23R
+ Δ – 18, since if Δ and R are both large, our algorithm
achieves a smaller latency. Large Δ and R are frequent
especially in large-scale, dense networks. The key behi-
nd-the-scene ideas of our algorithm include reducing the
number of blue nodes and maximal non-conflicting tra-
nsmission schedule sets in data aggregation scheduling.
Our algorithm has three phases: 1) Construct MIS Layer
by Layer; 2) Data Aggregation Tree Construction reduc-
ing the number of blue nodes; 3) Data Aggregation Sch-
eduling based on maximal non-conflicting transmission
schedule sets.
The details of our algorithm are showed in the next fo-
ur subsections. To better understand our algorithm, some
examples are given in these four subsections.
3.1. Construct MIS Layer by Layer
This phase is the same as [1]. For a given graph G = (V,
E) and the sink node s  V, a Breadth First Search Tree
(BFST) rooted at s for the graph G is firstly constructed.
In this phase, BFS starts at sink node s, which is the root
of BFST at layer 0, then BFS explores all the neighbor-
ing nodes which are added into BFST to be the children
of s at layer 1. Then, the new nodes adjacent to layer 1
nodes are added into BFST at layer 2 to be the children
of the nodes at layer 1, and so on. The BFS traversal ter-
minates when every node in V has been visited. For ex-
ample, Figure 2 shows a topology of G. Node 0 is the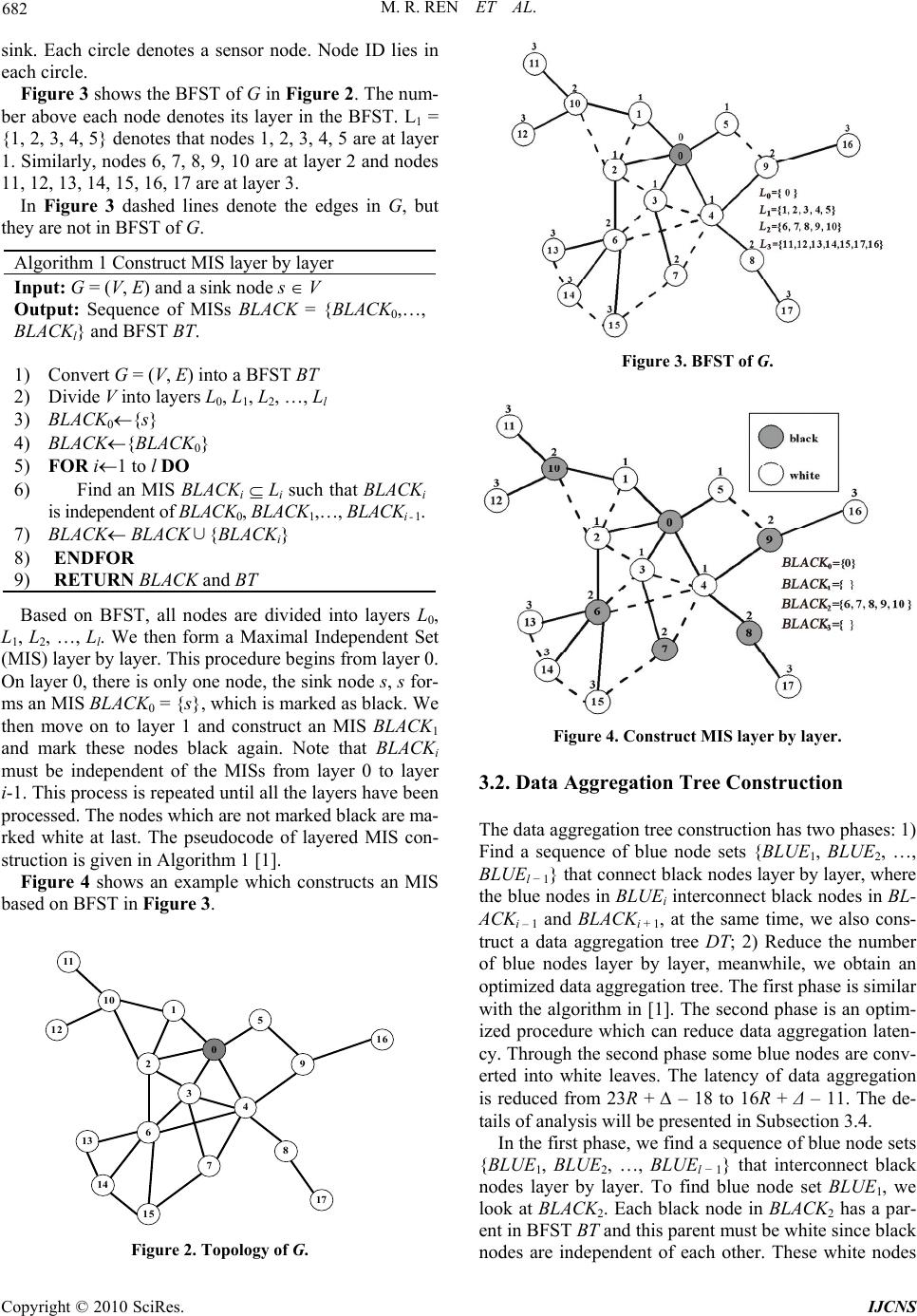

682 M. R. REN ET AL.
sink. Each circle denotes a sensor node. Node ID lies in
each circle.
Figure 3 shows the BFST of G in Figure 2. The num-
ber above each node denotes its layer in the BFST. L1 =
{1, 2, 3, 4, 5} denotes that nodes 1, 2, 3, 4, 5 are at layer
1. Similarly, nodes 6, 7, 8, 9, 10 are at layer 2 and nodes
11, 12, 13, 14, 15, 16, 17 are at layer 3.
In Figure 3 dashed lines denote the edges in G, but
they are not in BFST of G.
Algorithm 1 Construct MIS layer by layer
Input: G = (V, E) and a sink node s  V
Output: Sequence of MISs BLACK = {BLACK0,…,
BLACKl} and BFST BT.
1) Convert G = (V, E) into a BFST BT
2) Divide V into layers L0, L1, L2, …, Ll
3) BLACK0{s}
4) BLACK{BLACK0}
5) FOR i1 to l DO
6) Find an MIS BLACKi  Li such that BLACKi
is independent of BLACK0, BLACK1,…, BLACKi - 1.
7) BLACK BLACK∪{BLACKi}
8) ENDFOR
9) RETURN BLACK and BT
Based on BFST, all nodes are divided into layers L0,
L1, L2, …, Ll. We then form a Maximal Independent Set
(MIS) layer by layer. This procedure begins from layer 0.
On layer 0, there is only one node, the sink node s, s for-
ms an MIS BLACK0 = {s}, which is marked as black. We
then move on to layer 1 and construct an MIS BLACK1
and mark these nodes black again. Note that BLACKi
must be independent of the MISs from layer 0 to layer
i-1. This process is repeated until all the layers have been
processed. The nodes which are not marked black are ma-
rked white at last. The pseudocode of layered MIS con-
struction is given in Algorithm 1 [1].
Figure 4 shows an example which constructs an MIS
based on BFST in Figure 3.
11
1
10
0
13
8
5
3
7
2
14
12
6
15
4
9
16
17
Figure 2. Topology of G.
Figure 3. BFST of G.
Figure 4. Construct MIS layer by layer.
3.2. Data Aggregation Tree Construction
The data aggregation tree construction has two phases: 1)
Find a sequence of blue node sets {BLU E1, BLUE2, …,
BLUEl − 1} that connect black nodes layer by layer, where
the blue nodes in BLUEi interconnect black nodes in BL-
ACKi – 1 and BLACKi + 1, at the same time, we also cons-
truct a data aggregation tree DT; 2) Reduce the number
of blue nodes layer by layer, meanwhile, we obtain an
optimized data aggregation tree. The first phase is similar
with the algorithm in [1]. The second phase is an optim-
ized procedure which can reduce data aggregation laten-
cy. Through the second phase some blue nodes are conv-
erted into white leaves. The latency of data aggregation
is reduced from 23R + ∆ – 18 to 16R + Δ – 11. The de-
tails of analysis will be presented in Subsection 3.4.
In the first phase, we find a sequence of blue node sets
{BLUE1, BLUE2, …, BLUEl − 1} that interconnect black
nodes layer by layer. To find blue node set BLUE1, we
look at BLACK2. Each black node in BLACK2 has a par-
ent in BFST BT and this parent must be white since black
nodes are independent of each other. These white nodes

M. R. REN ET AL.
683
are colored blue and an edge between black node and its
white parent is added into data aggregation tree DT. Mo-
reover, the blue node must be connected with the black
node s in BLACK0. The edge between the blue node and
the black node s is added into DT. Note that to find blue
node set BLUEi, we color the parent of each black node
in BLACKi + 1 blue. The blue node must be connected
with the black node in BLACKi or BLACKi – 1. This proc-
ess is repeated layer by layer and finally a sequence of
blue node sets BLUE = {BLUE1, BLUE2, …, BLUEl – 1}
and a desired data aggregation tree DT are both obtained.
The pseudo code is presented in Algorithm 2.
Figure 5 shows an example of finding a sequence of
blue node sets based on the MIS in Figure 4.
In the second phase, we reduce the number of blue no-
des layer by layer and get an optimized data aggregation
tree. The purpose of reducing the number of blue nodes
is to reduce data aggregation latency. Recall the algori-
thm analysis in [1], the data aggregation latency greatly
depends on how many blue nodes lie inside the transmis-
sion range of a black node. A small number of blue nodes
results in a short data aggregation latency.
Algorithm 2 Finding blue node sets
Input: G = (V, E); Sink node sV; Sequence of MISs
BLACK = {BLACK0, …, BLACKl}; BFST BT.
Output: Sequence of blue node sets BLUE={BLUE1,
BLUE2, …, BLUEl - 1} and data aggregation tree DT
1) Procedure FindBlueNodeSets(G, s, BLACK, BT)
2) DT = (VDT,EDT ); VDT V; EDT ; BLUE;
3) //Find blue node sets that connect black nodes
4) FOR i1 to l-1 DO
5) FOR each black nodes uBLACKi + 1 DO
6) Find u’s parent pBT(u) in BFST BT
7) Color pBT(u) blue
8) Add pBT(u) to BLUEi
9) Add an edge (u, pBT(u)) to EDT
10) Find a black node v which can commu-
nicate with pBT(u) from BLACKi ∪BLACKi - 1
11) Add an edge (pBT(u), v) to EDT
12) ENDFOR
13) BLUE BLUE ∪BLUEi
14) ENDFOR
15) //Color remaining nodes white/
16) FOR each remaining node u DO
17) Color u white
18) Find u’s parent pBT(u) in BFST BT
19) Add an edge (u, pBT(u)) to EDT
20) ENDFOR
21) RETURN BLUE and DT
For a black node u, we only keep those blue nodes that
can communicate with u’s 2-hop black neighbors. For a
clear description, some concepts are given as follows.
Definition 4 [Coverage and Coverage Density] For a
blue node v  BLUEi + 1, a subset of BLACKi + 2 Cover-
age(v)  BLACKi + 2, is called v’s Coverage if v can
communicate with each black node in Cover ag e(v), i.e. v
can Cover all black nodes in Coverage(v). The cardinal-
ity of Coverage(v) is called v’s Coverage Density.
For a black node u  BLACKi, we only keep the blue
nodes in BLUEi + 1 that can cover u’s 2-hop black neig-
hbors in BLACKi + 2. The following lemma indicates that
we can keep at most 13 blue nodes which can cover u’s
2-hop black neighbors in BLACKi + 2.
Lemma 3.1 For a black node u  BLACKi (i = 0, 1, …,
l – 2), there are at most 13 blue nodes which can cover
u’s 2-hop black neighbors in BLACKi + 2.
Proof: For a black node u  BLACKi (i = 0, 1, …, l –
2), suppose there are at least 14 blue nodes c1, c2,…,c14
which can cover u’s 2-hop black neighbors in BLACKi + 2.
Assume that the transmission radius of a sensor node
is 1. Consider D2u, a circular of radius 2 centered at the bl-
ack node u. All u’s 2-hop black neighbors lie inside D2u.
Since black nodes are mutually independent, for each bl-
ack node in D2u, we consider a circular of radius 0.5 cen-
tered at this black node, then all of those circulars must
be disjoint. u’s blue children nodes lie inside D1u, a circ-
ular of radius 1 centered at the black node u.
Since we suppose there are at least 14 blue nodes c1,
c2,…,c14 which can cover u’s 2-hop black neighbors,
then each of u’s 2-hop black neighbors can be covered at
least by one blue node of those 14 blue nodes. From u’s
2-hop black neighbors, we certainly find at least 14 bla-
ck nodes b1, b2,…,b14 such that bi (i = 1,2,…,14) is cove-
red only by ci (i = 1,2,…,14) and u’s other 2-hop black
neighbors besides these 14 black nodes b1, b2,…,b14 are
covered at least by two blue nodes. (If we can not find at
least 14 black nodes b1, b2,…,b14, then there are at most
13 blue nodes which can cover u’s 2-hop black neighbors.
The lemma is proved.) These 14 black nodes b1, b2,…,
b14 certainly lie outside the circular D1u and inside the
Figure 5. Finding blue node sets.

684 M. R. REN ET AL.
circular D2u centered at the black node u. (Refer to Fig-
ure 6) We equably divide D2u into 13 sectors. According
to the pigeonhole principle [13], there are two black nod-
es at least lie inside the same sector, i.e. there are at least
2 circulars of radius 0.5 centered at black nodes lie inside
the same sector. Without loss of generality, suppose bla-
ck nodes b1 and b2 lie inside the same sector, and b1 is fa-
rther than b2 from u. Since blue node c1 covers b1. Obvi-
ously, c1 covers b2 too. (This fact can be simply validated
by geometry. Refer to Figure 6.) This is contradictory to
that b2 is covered only by c2, since b2 is covered by both
c1 and c2. Therefore, the above assumption is false. This
lemma is proved.
Algorithm 3 Reducing the number of blue nodes
Input: G = (V, E); Sequence of MISs BLACK; BFST
BT; Sequence of blue node sets BLUE; Data aggrega-
tion tree DT.
Output: Reduced data aggregation tree based on DT.
1) Procedure ReduceBlueNodes (G, BLACK, BT,
BLUE, DT)
2) //Reduce the number of blue nodes layer by layer
3) FOR i0 to l – 2 DO
4) NEWBLUE
5) FOR each black nodes u  BLACKi DO
6) Find u’s blue children set BC(u)  BLUEi + 1
7) Find u’s 2-hop black neighbors set BN(u)
8) Descending sort BC(u) on the coverage density
9) WHILE BN(u)   DO
10) Get out a blue node x from BC(u)
11) BC(u)BC(u) − {x}
12) NEWBLU E NEWBLUE∪{x}
13) FOR each wCoverage(x) DO
14) Remove edge (w, pDT(w)) from
EDT
15) Add edge (x, w) into EDT
16) ENDFOR
17) BN(u)BN (u) − Coverage(x)
18) ENDWHILE
19) ENDFOR
20) Color nodes in BLUEi + 1 − NEWBLUE from
blue to white;
21) BLUE
i + 1  NEWBLUE
22) ENDFOR
23) RETURN DT
According to Lemma 3.1, we design Algorithm 3 to
reduce the number of blue nodes. The idea of Algorithm
3 is based on a greedy strategy. For each black node u 
BLACKi, we find u’s blue children set BC(u)  BLUEi + 1
and u’s 2-hop black neighbors set BN(u), then we sort
BC(u) in a decreasing order on the coverage density. In
the first repetition, we keep the blue node x which has
the largest coverage density, and remove x from BC(u).
For each w  Coverage(x), we remove edge (w, p(w))
from the data aggregation tree and add edge (x, w) into
the data aggregation tree. The covered black node set
Coverage(x) by blue node x is removed from BN(u). This
process is terminated until BN(u) is an empty set. Algo-
rithm 3 is executed layer by layer. Finally, the rest blue
nodes are converted from blue to white.
The pseudo code is presented in Algorithm 3. For
convenience, the output of Algorithm 3 is called Reduced
Data Aggregation Tree. Figure 7 shows an example of
reducing the number of blue nodes based on the result in
Figure 5.
To construct a data aggregation tree, we firstly execute
Algorithm 2 to find a sequence of blue node sets {BLUE1,
BLUE2, …, BLUEl − 1} that connect black nodes layer by
layer and construct a data aggregation tree DT; Second,
Algorithm 3 is executed to reduce the number of blue no-
des layer by layer, and finally we obtain a data aggrega-
tion tree. The pseudocode of the entire procedure of data
aggregation tree construction is presented in Algorithm
4.
Figure 6. Proof of lemma 3.1.
Figure 7. Reducing the number of blue nodes.

M. R. REN ET AL.
685
Algorithm 4 Data Aggregation tree construction
Input: G = (V, E); Sink node sV; Sequence of maxi-
mal independent sets BLACK; BFST BT .
Output: A reduced data aggregation tree RDT
1) Execute FindBlueNodeSets (G, s, BLACK, BT) to
obtain BLUE and DT;
2) RDTReduceBlueNodes (G, BLACK, BT, BLUE,
DT);
3) RETURN RDT
3.3. Data Aggregation Scheduling
In this section, we generate a data aggregation schedule
based on the data aggregation tree. The process of gener-
ating a data aggregation schedule is simple and it breaks
the transmission rule of white nodes sending to black
nodes, black nodes sending to blue nodes and blue nodes
sending to black nodes. The process of data aggregation
scheduling is the process of cutting leaves.
The process of data aggregation scheduling takes in an
input of a network topology G = (V, E) and a correspo-
nding data aggregation tree DT. First, we pick a node u
from the leaves of DT and generate a transmission sch-
edule u → pDT(u), where pDT(u) is u’s parent in DT, then
we check whether u → pDT(u) conflicts with any trans-
mission schedule in the current non-conflicting transmis-
sion schedule set Si (its initial value is null, i = 1,2,…). If
it does not conflict with any transmission schedule in Si,
then we add u → pDT(u) to Si. Otherwise, we check the
next transmission schedule using a leaf of DT as the
sender. Finding a maximal non-conflicting transmission
schedule set based on the leaves of DT is similar with 0-1
knapsack problem and we present an approximate algor-
ithm in Algorithm 5 due to it is NP-hardness. We do not
prove the problem of finding a maximal non-conflicting
transmission schedule set to be NP-hard due to page lim-
itation. When we obtain a maximal non-conflicting trans-
mission schedule set from the leaves of DT, we cut these
leaves and edges associated with these leaves and their
parents. This process is repeated until there is only one
sink node s in DT.
Algorithm 5 Data Aggregation Scheduling
Input: G = (V, E); Sink sV; Data aggregation tree DT
Output: Data aggregation schedule S
1) i1; S{};
2) WHILE there exists an edge in DT DO
3) Si
4) Leaves{u| u a is leaf of DT}
5) WHILE Leaves  DO
6) FOR each leaf u in Leaves DO
7) FOR each x→pDT(x)Si DO
8) IF Si= or uNeighbor(x) and
pDT(x)Neighbor(u)
9) Si Si ∪{ u→pDT(u)}
10) ENDIF
11) ENDFOR
12) ENDFOR
13) ENDWHIL E
14) FOR each schedule u→pDT(u) in Si DO
15) Cut edge (u, pDT(u))from DT
16) ENDFOR
17) S S∪Si; ii + 1;
18) ENDWHILE
The pseudo code of data aggregation scheduling is pre-
sented in Algorithm 5. Note that in Algorithm 5, we con-
sider two types of collisions discussed in Figure 1, whe-
reas the transmission rule of FIRSTFIT in [1] only con-
siders type (a) in Figure 1.
As an example, given the reduced data aggregation tr-
ee in Figure 7, the final data aggregation schedule is giv-
en as follows: S1 = {11 → 10; 13 → 6; 7 → 4; 17 → 8; 5
→ 0;} S2 = {12 → 10; 14 → 6; 8 → 4; 16 → 9;} S3 =
{10 → 1; 15 → 6; 9 → 4;} S4 = {1 → 0; 6 → 4;} S5 = {2
→ 0;} S6 = {3 → 0;} S7 = {4 → 0;}.
Let L5−RDT denote the data aggregation latency of Al-
gorithm 5. Then for this example we have L5−RDT = 7.
Lemma 3.2 For a given data aggregation tree DT, the
data aggregation latency of Algorithm 5 is no more than
that of Algorithm 4 in [1].
Proof: Algorithm 4 in [1] has the aptotic transmission
rule of white nodes sending to black nodes, black nodes
sending to blue nodes and blue nodes sending to black no-
des. Nevertheless, our Algorithm 5 does not follow this
rule. Algorithm 5 picks nodes from the leaves of the data
aggregation tree DT and generates transmission schedu-
les. Furthermore, some black nodes are possibly leaves.
For example, in Figure 7, node 7 is a black leaf.
Without loss of generality, for all the leaves of DT,
there are m white nodes and a black node b. According to
the transmission rule of FIRSTFIT in [2], the m white
nodes and the black node b are definitely in different se-
nder sets Sender(Si),…, Sender(Sj − 1), Sender(Sj) (i < j)
such that m white nodes are in Sender(Si),…, Sender(Sj − 1)
and b is in Sender(Sj), where Si,…, Sj − 1, Sj are transmis-
sion schedule sets. Moreover, according to the transmis-
sion rule of Algorithm 5, m white nodes are in Sender
(Si),…, Sender(Sj − 1) and either b is in Sender(Sj) if b
→ pDT(u) conflicts with transmission schedules in Si, …,
Sj − 1 or b is in Sender(Sk) (i  k  j − 1) if b → pDT(u)
does not conflict with transmission schedules in Si, …, Sj
− 1. Thus, the data aggregation latency of Algorithm 5 is
no more than that of Algorithm 4 in [1]. After cutting le-
aves from the current data aggregation tree, similar proof
can be applied on the residual data aggregation tree.
For example, given the reduced data aggregation tree

686 M. R. REN ET AL.
in Figure 7, the final data aggregation schedule based on
FIRSTFIT in [1] is given as follows:
WHITE to BLACK
S1 = {5 → 0; 11 → 10; 13 → 6; 17 → 8;}
S2 = {16 → 9; 14 → 6; 12 → 10; 3 → 0;}
S3 = {15 → 6;}
S4 = {2 → 0;};
BLACK to BLUE
S5 = {10 → 1; 9 → 4;}
S6 = {6 → 4;}
S7 = {7 → 4;}
S8 = {8 → 4;};
BLUE to BLACK
S9 = {1 → 0;}
S10 = {4 → 0;}.
Let L4[2]−RDT denote the data aggregation latency of Al-
gorithm 4 in [1] taking in an input of a reduced data ag-
gregation tree, then for this example we have L4[2]−RDT =
10 > L5−RDT = 7.
3.4. Performance Analysis
In this section we show that Algorithm 5 has a latency
bound of 16R + Δ – 11. Suppose that DT is a data aggre-
gation tree generated by Algorithm 2 and RDT is a redu-
ced data aggregation tree generated by Algorithm 3 tak-
ing in an input of DT. Let L4[2]−DT denote the data aggre-
gation latency of Algorithm 4 in [1] taking in an input of
DT, L
4[2]−DT = 23R + Δ – 18; If we could estimate
L4[2]−RDT = 16R + Δ – 11, according to Lemma 3.2, there
is L5−RDT  L4[2]−RDT, then L5−RDT  16R + Δ – 11, i.e. Al-
gorithm 5 has a latency bound of 16R + Δ – 11.
Now, let’s estimate L4[2]−RDT = 16R + Δ – 11. The tran-
smission rule of Algorithm 4 in [1] has three parts: 1)
WHITE to BLACK; 2) BLACK to BLUE; 3) BLUE to
BLACK.
1) WHITE to BLACK: It takes at most Δ – 1 time slots
[2] to finish the transmission.
2) BLACK to BLUE: It takes at most 4 time slots to
finish the transmission.
3) BLUE to BLACK: We need to estimate how many
blue nodes are competing to transmit to the same black
parent. According to Lemma 3.1, we know that for a
fixed black node u  BLACKi (i = 0, 1, …, l – 2), there
are at most 13 blue nodes which can cover u’s 2-hop bla-
ck neighbors in BLACKi + 2. One of these 13 blue nodes
must be node u’s parent. Therefore, there are at most 12
blue nodes which are competing to transmit to the same
black parent.
WHITE-to-BLACK needs Δ – 1 time slots. From layer
R to layer 2, BLACK-to-BLUE and BLUE-to-BLACK
together need (12 + 4)·(R – 2) time slots. Transmission
from layer 2 to layer 1 needs 13 + 4 time slots and trans-
mission from layer 1 to the sink needs 5 time slots. Al-
together,
L4[2]−RDT = (Δ – 1) + (12 + 4)·(R - 2) + 13 + 4 + 5
= 16R + Δ – 11.
Therefore, L5−RDT  L4[2]−RDT < L4[2]−DT = 23R + Δ – 18,
i.e. Algorithm 5 has a latency bound of 16R + Δ – 11.
Lemma 3.3 If R ≥ Δ – 11, our algorithm has approxi-
mation ratio 17.
Proof: Given a graph G = (V, E) and the sink node s 
V, let Lopt denote the minimum data aggregation latency.
Since farthest node has to transmit data to the sink, the-
refore Lopt ≥ R. L5−RDT / Lopt  (16R + Δ – 11) / R  16 +
(Δ – 11) / R, when R ≥ Δ – 11, L5−RDT/Lopt  17.
Lemma 3.4 If R is enough large, our algorithm has
approximation ratio 16 from an asymptotic point of view.
Proof: According to the proof of lemma 3.3, when R
tends to infinite, (Δ – 11)/R tends to zero, therefore our
algorithm has approximation ratio 16 from an asymptotic
point of view.
For example, given a data aggregation tree DT without
reducing the number of blue nodes in Figure 5, the final
data aggregation schedule generated by Algorithm 4 in
[1] is given as follows:
WHITE to BLACK S1 = {5 → 0; 11 → 10; 13 → 6;
17 → 8;} S2 = {16 → 9; 14 → 6; 12 → 10;} S3 = {15 →
6;}; BLACK to BLUE S4 = {10 → 1; 9 → 4;} S5 = {6 →
2;} S6 = {7 → 3;} S7 = {8 → 4;} BLUE to BLACK S8 =
{1 → 0;} S9 = {2 → 0;} S10 = {3 → 0;} S11 = {4 → 0;}.
In this example, we have L4[2]−DT = 11. For the exam-
ple of the topology shown in Figure 2, we have: L5−RDT =
7 < L4[2]−RDT = 10 < L4[2]−DT = 11.
4. Simulation Results
In this section, we evaluate our work by conducting exte-
nsive simulations. We compare our algorithm with Algo-
rithm 4 in [1]. In the following, we first explain the obje-
ctive of the simulations, the generation of a network and
performance metric we used. Then we present the simul-
ation results. There are two main factors that affect the
data aggregation latency, network radius R and the ma-
ximum degree of network topology Δ. The objective of
the simulations is straightforward, that is to investigate
the effects of R and Δ on the data aggregation latency.
The performance metric is the number of transmission
schedule sets in data aggregation schedule {S1, S2, …, Sl},
i.e. the value of l. The smaller l means that the better the
algorithm performance.
We also implemented a topology simulator that can ra-
ndomly deploy sensors into a square region of size X × X,
where X is the width of the square. The topology simu-
lator takes in an input of a network radius R, a maximum
degree of network topology Δ, a transmission range of
each sensor node r. R is the length of the longest path in
data aggregation tree DT from the sink to the leaf nodes
of DT, i.e. the largest number of hops from the sink to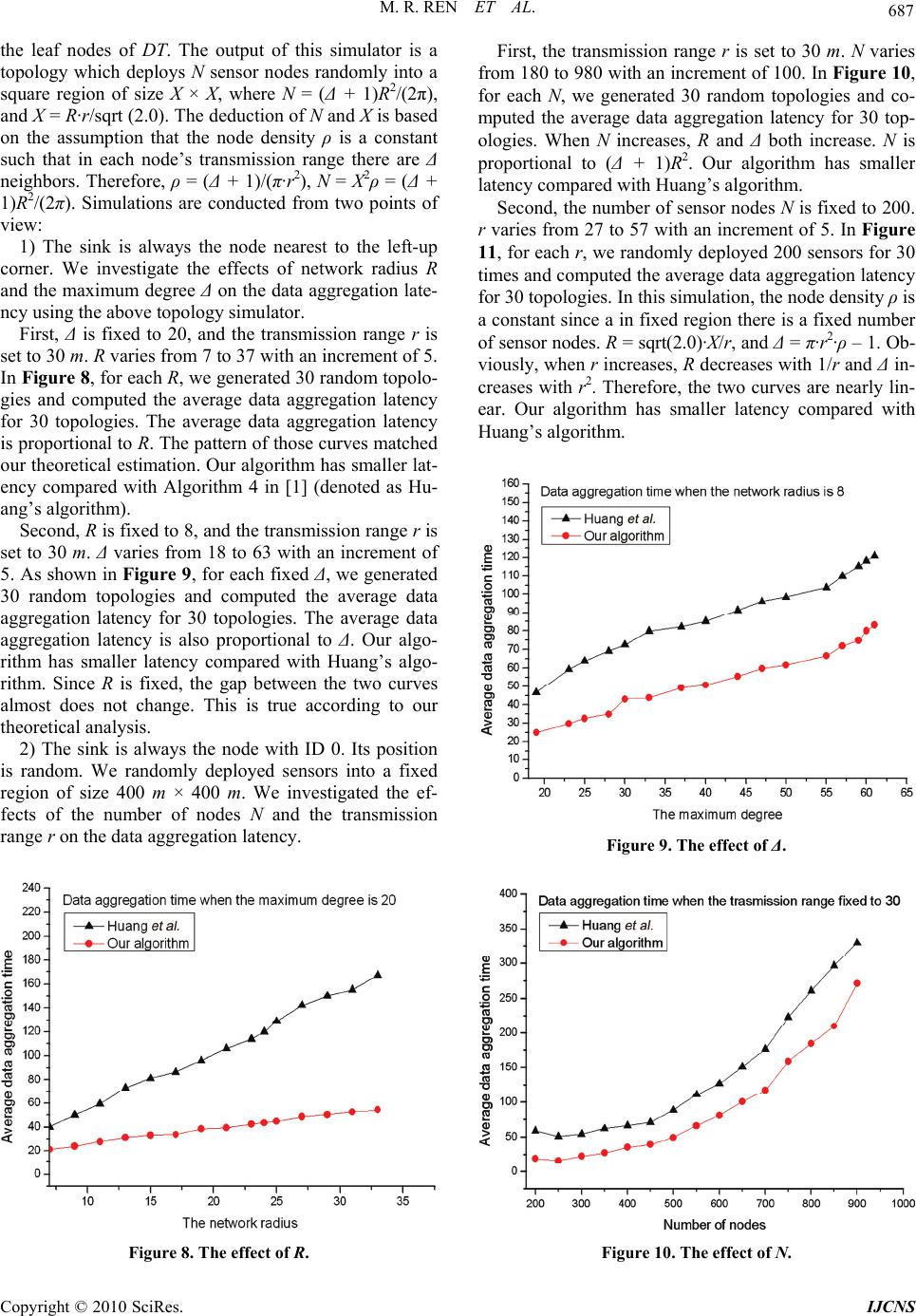

M. R. REN ET AL.
687
the leaf nodes of DT. The output of this simulator is a
topology which deploys N sensor nodes randomly into a
square region of size X × X, where N = (Δ + 1)R2/(2π),
and X = R·r/sqrt (2.0). The deduction of N and X is based
on the assumption that the node density ρ is a constant
such that in each node’s transmission range there are Δ
neighbors. Therefore, ρ = (Δ + 1)/(π·r2), N = X2ρ = (Δ +
1)R2/(2π). Simulations are conducted from two points of
view:
1) The sink is always the node nearest to the left-up
corner. We investigate the effects of network radius R
and the maximum degree Δ on the data aggregation late-
ncy using the above topology simulator.
First, Δ is fixed to 20, and the transmission range r is
set to 30 m. R varies from 7 to 37 with an increment of 5.
In Figure 8, for each R, we generated 30 random topolo-
gies and computed the average data aggregation latency
for 30 topologies. The average data aggregation latency
is proportional to R. The pattern of those curves matched
our theoretical estimation. Our algorithm has smaller lat-
ency compared with Algorithm 4 in [1] (denoted as Hu-
ang’s algorithm).
Second, R is fixed to 8, and the transmission range r is
set to 30 m. Δ varies from 18 to 63 with an increment of
5. As shown in Figure 9, for each fixed Δ, we generated
30 random topologies and computed the average data
aggregation latency for 30 topologies. The average data
aggregation latency is also proportional to Δ. Our algo-
rithm has smaller latency compared with Huang’s algo-
rithm. Since R is fixed, the gap between the two curves
almost does not change. This is true according to our
theoretical analysis.
2) The sink is always the node with ID 0. Its position
is random. We randomly deployed sensors into a fixed
region of size 400 m × 400 m. We investigated the ef-
fects of the number of nodes N and the transmission
range r on the data aggregation latency.
Figure 8. The effect of R.
First, the transmission range r is set to 30 m. N varies
from 180 to 980 with an increment of 100. In Figure 10,
for each N, we generated 30 random topologies and co-
mputed the average data aggregation latency for 30 top-
ologies. When N increases, R and Δ both increase. N is
proportional to (Δ + 1)R2. Our algorithm has smaller
latency compared with Huang’s algorithm.
Second, the number of sensor nodes N is fixed to 200.
r varies from 27 to 57 with an increment of 5. In Figure
11, for each r, we randomly deployed 200 sensors for 30
times and computed the average data aggregation latency
for 30 topologies. In this simulation, the node density ρ is
a constant since a in fixed region there is a fixed number
of sensor nodes. R = sqrt(2.0)·X/r, and Δ = π·r2·ρ – 1. Ob-
viously, when r increases, R decreases with 1/r and Δ in-
creases with r2. Therefore, the two curves are nearly lin-
ear. Our algorithm has smaller latency compared with
Huang’s algorithm.
Figure 9. The effect of Δ.
Figure 10. The effect of N.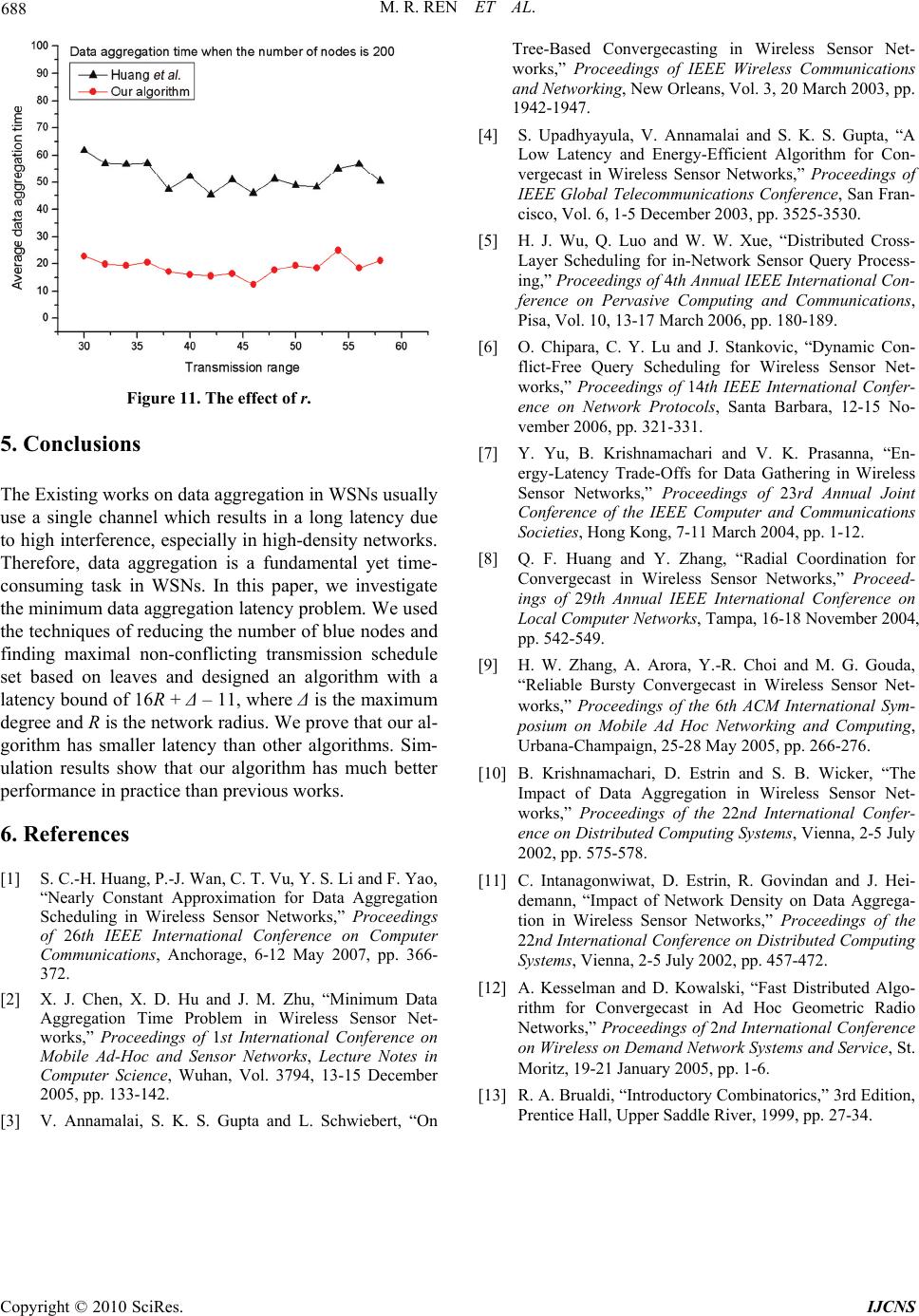

M. R. REN ET AL.
688
Figure 11. The effect of r.
5. Conclusions
The Existing works on data aggregation in WSNs usually
use a single channel which results in a long latency due
to high interference, especially in high-density networks.
Therefore, data aggregation is a fundamental yet time-
consuming task in WSNs. In this paper, we investigate
the minimum data aggregation latency problem. We used
the techniques of reducing the number of blue nodes and
finding maximal non-conflicting transmission schedule
set based on leaves and designed an algorithm with a
latency bound of 16R + Δ – 11, where Δ is the maximum
degree and R is the network radius. We prove that our al-
gorithm has smaller latency than other algorithms. Sim-
ulation results show that our algorithm has much better
performance in practice than previous works.
6. References
[1] S. C.-H. Huang, P.-J. Wan, C. T. Vu, Y. S. Li and F. Yao,
“Nearly Constant Approximation for Data Aggregation
Scheduling in Wireless Sensor Networks,” Proceedings
of 26th IEEE International Conference on Computer
Communications, Anchorage, 6-12 May 2007, pp. 366-
372.
[2] X. J. Chen, X. D. Hu and J. M. Zhu, “Minimum Data
Aggregation Time Problem in Wireless Sensor Net-
works,” Proceedings of 1st International Conference on
Mobile Ad-Hoc and Sensor Networks, Lecture Notes in
Computer Science, Wuhan, Vol. 3794, 13-15 December
2005, pp. 133-142.
[3] V. Annamalai, S. K. S. Gupta and L. Schwiebert, “On
Tree-Based Convergecasting in Wireless Sensor Net-
works,” Proceedings of IEEE Wireless Communications
and Networking, New Orleans, Vol. 3, 20 March 2003, pp.
1942-1947.
[4] S. Upadhyayula, V. Annamalai and S. K. S. Gupta, “A
Low Latency and Energy-Efficient Algorithm for Con-
vergecast in Wireless Sensor Networks,” Proceedings of
IEEE Global Telecommunications Conference, San Fran-
cisco, Vol. 6, 1-5 December 2003, pp. 3525-3530.
[5] H. J. Wu, Q. Luo and W. W. Xue, “Distributed Cross-
Layer Scheduling for in-Network Sensor Query Process-
ing,” Proceedings of 4th Annual IEEE International Con-
ference on Pervasive Computing and Communications,
Pisa, Vol. 10, 13-17 March 2006, pp. 180-189.
[6] O. Chipara, C. Y. Lu and J. Stankovic, “Dynamic Con-
flict-Free Query Scheduling for Wireless Sensor Net-
works,” Proceedings of 14th IEEE International Confer-
ence on Network Protocols, Santa Barbara, 12-15 No-
vember 2006, pp. 321-331.
[7] Y. Yu, B. Krishnamachari and V. K. Prasanna, “En-
ergy-Latency Trade-Offs for Data Gathering in Wireless
Sensor Networks,” Proceedings of 23rd Annual Joint
Conference of the IEEE Computer and Communications
Societies, Hong Kong, 7-11 March 2004, pp. 1-12.
[8] Q. F. Huang and Y. Zhang, “Radial Coordination for
Convergecast in Wireless Sensor Networks,” Proceed-
ings of 29th Annual IEEE International Conference on
Local Computer Networks, Tampa, 16-18 November 2004,
pp. 542-549.
[9] H. W. Zhang, A. Arora, Y.-R. Choi and M. G. Gouda,
“Reliable Bursty Convergecast in Wireless Sensor Net-
works,” Proceedings of the 6th ACM International Sym-
posium on Mobile Ad Hoc Networking and Computing,
Urbana-Champaign, 25-28 May 2005, pp. 266-276.
[10] B. Krishnamachari, D. Estrin and S. B. Wicker, “The
Impact of Data Aggregation in Wireless Sensor Net-
works,” Proceedings of the 22nd International Confer-
ence on Distributed Computing Systems, Vienna, 2-5 July
2002, pp. 575-578.
[11] C. Intanagonwiwat, D. Estrin, R. Govindan and J. Hei-
demann, “Impact of Network Density on Data Aggrega-
tion in Wireless Sensor Networks,” Proceedings of the
22nd International Conference on Distributed Computing
Systems, Vienna, 2-5 July 2002, pp. 457-472.
[12] A. Kesselman and D. Kowalski, “Fast Distributed Algo-
rithm for Convergecast in Ad Hoc Geometric Radio
Networks,” Proceedings of 2nd International Conference
on Wireless on Demand Network Systems and Service, St.
Moritz, 19-21 January 2005, pp. 1-6.
[13] R. A. Brualdi, “Introductory Combinatorics,” 3rd Edition,
Prentice Hall, Upper Saddle River, 1999, pp. 27-34.