Int. J. Communications, Network and System Sciences, 2010, 3, 674-678
doi:10.4236/ijcns.2010.38090 Published Online August 2010 (http://www.SciRP.org/journal/ijcns)
Application of Perfect Difference Codes in Wireless
Infrared Systems
Fahim A. Umrani, Salah Obayya
Faculty of Advanced Technology, University of Glamorgan, Pontypridd, UK
Received February 8, 2010; revised May 3, 2010; accepted June 19, 2010
Abstract
In this paper, we apply the perfect difference codes in wireless infrared systems considering the diffuse in-
door optical wireless configuration. The bit error rate performance of the uplink wireless infrared system us-
ing Gaussian approximations is analyzed taking into account the effects of multiple-access interference, the
ambient light noise, and the dark current. The proposed system also uses the compact encoder and decoder
architecture resulting in a low cost system.
Keywords: OCDMA, Compact Encoder/Decoder, Perfect Difference Codes
1. Introduction
The past few decades have seen the increased interest of
the researchers in the utilization of infrared (IR) frequenc-
ies for short range wireless communications [1-5]. Wire-
less radio technologies have been designed and implem-
ented comparatively over a much longer time than wire-
less infrared systems, however, the low complexity and
low cost of infrared systems make relatively new IR sys-
tems very attractive and cost effective solution at a bit
rates up to several tens of Mbps. Many potential applica-
tions for this technology, such as Wireless LANs, have
already been suggested. Optical wireless networks are
suitable for “campus” networking, metropolitan commu-
nication infrastructure, rapid deployment in emergency
situations, disaster recovery, and in military contexts.
The diffuse indoor optical wireless configuration (i.e.
non-directed, non-line of sight) is one of the most conve-
nient and robust solution for local area networks (LAN).
In the diffuse configuration, the transmitters and the rec-
eivers of infrared systems do not require to be carefully
aligned, nor do they need to be in a line-of-sight (LOS)
path so that communication can be maintained. The other
major advantages of diffuse systems are their flexibility
and the roaming they allow in a room. This flexibility
makes them the ideal choice for ad hoc networks and
gives the end users freedom to roam freely insider the
office or room. Therefore, in this paper, we consider a
diffuse configuration. However, this freedom of roaming
results in the problems associated with high path loss and
inter-symbol interference (ISI) due to multipath disper-
sion. In a code-division based WIR systems, the effects
of ISI can be compensated by using efficient spreading
sequences, such as perfect difference codes (PDC) in sp-
ectral-amplitude coding based system [6].
Perfect difference codes are the special type of cyclic
difference set with weight (number of pulsed chips) equ-
als to w, length v = w2 – w + 1, and correlation constraint
of γ = 1. The detailed information about the perfect diff-
erence codes can be found in [7-9]. PDCs provide a co-
mpromise performance between the two typical classes
of unipolar sequences used in OCDMA systems, i.e.,
Optical Orthogonal codes and Prime codes, in terms of
cardinality, sequence length and cross correlation con-
straint. PDCs have cross correlation constraint equal to
OOC and sequence length comparable to Prime codes
with the added advantage that PDCs can be constructed
for any number of weight, while in Prime codes the wei-
ght is equal to a prime number. To the author’s best know-
ledge most work on WIR systems adopting unipolar se-
quences is based on either OOC and Prime codes [10-11],
we for the first time in this paper apply PDCs in wireless
infrared systems. For the purpose of this paper we are
interested in the following two properties of PDCs: 1)
The cross correlation between the two PDCs is unity.
This property is exploited to design the decoder to effi-
ciently recover data by suppressing MAI effect, and 2)
Perfect difference codes are cyclic shifted. The cyclic na-
ture of PDCs is combined with the cyclic nature of Ar-
rayed-waveguide multiplexers to construct compact effi-
cient encoders.
In this paper, we apply perfect difference codes for the

F. A. UMRANI ET AL.
675
first time in indoor optical wireless channel. A wireless
infrared system is proposed which uses the compact enc-
oders and decoders. The uplink performance analysis of
such system is analyzed in terms of bit error rate versus
path loss and bit error rate versus number of users.
Following this, in Section 2 we give the reader an in-
troduction and overview of the system model explaining
the channel model and transmitter receiver structure to
clarify the analysis presented in the next section. We gi-
ve the schematic diagram of the encoding and decoding
device and explain how they work. In Section 3, we ob-
tain the system performance under Gaussian approxima-
tions using the proposed model in Section 2. Finally Sec-
tion 4 concludes the paper.
2. System Model
The number of active users is I + 1 and Nmax is maximum
allowed number of users which can be associated to each
station. We use PDC based OCDMA as uplink multiple
access technique. The average received power using
PDC is expressed by [12]
drr AI
v
w
P2  (1)
where Ir = is the received light intensity,
Ad = is the area of photodetector.
2.1. Channel Model
One of the most important parameters that affect the
performance of infrared system is the channel path loss
which is the DC-gain (H0) of the channel transfer func-
tion. It can be expressed as:
tr PHP 0
 (2)
relating the transmitted and received average powers.
Figure 1 illustrates the non-directed non-line of sight
configuration selected for the system under study in wh-
ich the transmitter and receiver are pointed straight up-
ward and transmitter emits a Lambertian pattern. The h1
and h2 represents the distance of transmitter and receiver
from the ceiling, with diffuse reflectivity ρ, respectively.
We assume that the diffuse reflectivity of ceiling is 80%.
The path loss for diffuse link is plotted in Figure 2 wh-
ich is measured in a typical office [4].
2.2. Transmitter & Receiver
At the transmitter on-off keying intensity modulation sc-
heme is adopted and direct detection at the receiver. Du-
ration of each chip is Tc = Tb/v where v is the code length
and Tb is the bit duration.
Figure 3 shows the proposed encoder designed with
PDCs for v = 7 and w = 3. It contains 1 × 7 splitter and
one 7 × 7 AWG router which can generate seven code-
words simultaneously. After the light is incident on the
splitter it is directed to 3 specific AWG input ports ac-
cording to the adopted PDC. By controlling the states of
2 × 2 switches denoted as dk with the user’s information
bits, the encoder can transmit suitable codewords to the
end users. The upper arm of 2 × 2 switch is connected to
the combiner for broadcast transmission, while the lower
arm is left unused. When the data bit is 1 a unique PDC
assigned to each user is sent, however, when data bit is 0,
a common zero code assigned to all users is transmitted
[13].
h1
Diffuse
reflectivity
Receiver
Transmitte
r
h2
Figure 1. Non-directed non-line of sight LOS (diffuse) con-
figuration.
Horizontal se
p
aration
(
m
)
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Path Loss (Optical dB)
70
65
60
55
50
45
Figure 2. Optical path loss of a diffuse infrared links empl-
oying a Lambertian transmitter and a detector of area Ad =
1 cm2 and reflectivity of 80% measured in a typical room.
Figure 3. Encoder based on PDC. (BS: Broadband source).

F. A. UMRANI ET AL.
676
At the receiver, a composite signal containing the des-
ired signal along with the noise and interference from all
other I active users passed through the channel is dete-
cted. The receiver’s structure as illustrated in Figure 4 is
based on correlation detection. The received signal is di-
vided into v branches and then delayed to accumulate the
marked chips in the optical correlator. At the receiver all
the weighted chips of the desired sequence are summed
to form a decision variable. This decision variable is com-
pared to a threshold to detect data bit 1 or 0 [14].
where




x
y
dyexQ 2
2
2
1

(6)
μb and σb is the mean and variance, respectively, of the
signal when data bit b (0 or 1) is transmitted, and θ is the
threshold.
Let Pr be the received optical power per chip at the
input of correlator, then power at the output of optical
correlator can be written as:



, for 1
, for 0
r
CR
r
Pw Ib
PPI b






(7)
3. Performance Analysis and Results
In this analysis, it is assumed that different nodes trans-
mit asynchronously and independently. Further to make
things simpler, different signals are assumed to be chip
synchronous, which is a pessimistic case and gives an
upper bound to the BER of the real asynchronous system
[14,15].
here w is the weight of the PDC, I is the number of in-
terfering users in the system.
The threshold Pth of the hard limiter is set to Pr (w +
2I)/2; therefore, the power Pr (w + I) in Equation (7) is
clipped to Pr (w + 2I)/2 while the power Pr (I) is clipped
to zero. After that, the output of the hard limiter is trans-
formed to an electronic signal by the photodetector. Fi-
nally, the integrate-and-dump circuit and the threshold
circuit decide whether the received bit is 0 or 1.
The number of interfering pulses received in jth pulse
position of the desired codeword is denoted by ,,
j21


. The vector of received interference is denoted by K,

K
,,,  
21
 
. In light of the cross-correlation
property of PDC, two code-words cannot overlap at more
than one pulse position. Therefore, the probability that
two codewords overlap at one pulse position is

q
where factor 1/2 accounts for the probability
that interfering user sent “one” only half time.
v/w 2
2
The average photon arrival rate λ per pulse at the input
of the optical correlator is given by λ = ηPr/hf. Accord-
ing to correlation property of PDC each user contributes
one spectral component in the desired user’s signal and
the mean photon count produced by the ith interferer,
which is a function of ρi (path loss) and transmission
power, is given is:
Given I interfering users, the BER of the desired
user’s signal can be expressed as [15,16]:
 
1
, 1,2,1
K
k
k
IikN 




(8)
 



I
i
ireFPiPP
0
(3)
Given N = I and the desired bit b = 1, using Gaussian
expression, the mean and variance can be expressed as:
where is the probability that there are l interfering
pulses, which is given by:
 iP
r




















hf
mA
GT
e
kI
R
Ik
GT bd
c
d
b
c
 

2
1 (9)
 
iI
i
rqq
i
I
iP  








1 (4)


2 2 2
1
2
th
bd
c
d
b
ce hf
mA
GT
e
kI
R
Ik
TFG 


 
















 (10)
i is the set of all possible
F  vectors. Since the I in-
terfering users are not distinguishable in correlation re-
ceiver,



 PFP i. where Ad is the photodetector’s area, mb is the mean
photon count of the ambient light noise, and Id is the dark
current, G is the average APD gain of upper APD. Tc is
the chip duration, Ib is the bulk leakage current, Is is the
surface leakage current, e is the electron charge, Fe is the
excess noise factor given as:
Using Gaussian approximation for photon detection,


 P can be written as [15,16]:



















1
1
0
05050




 Q.Q.P (5)
Figure 4. Decoder of the system.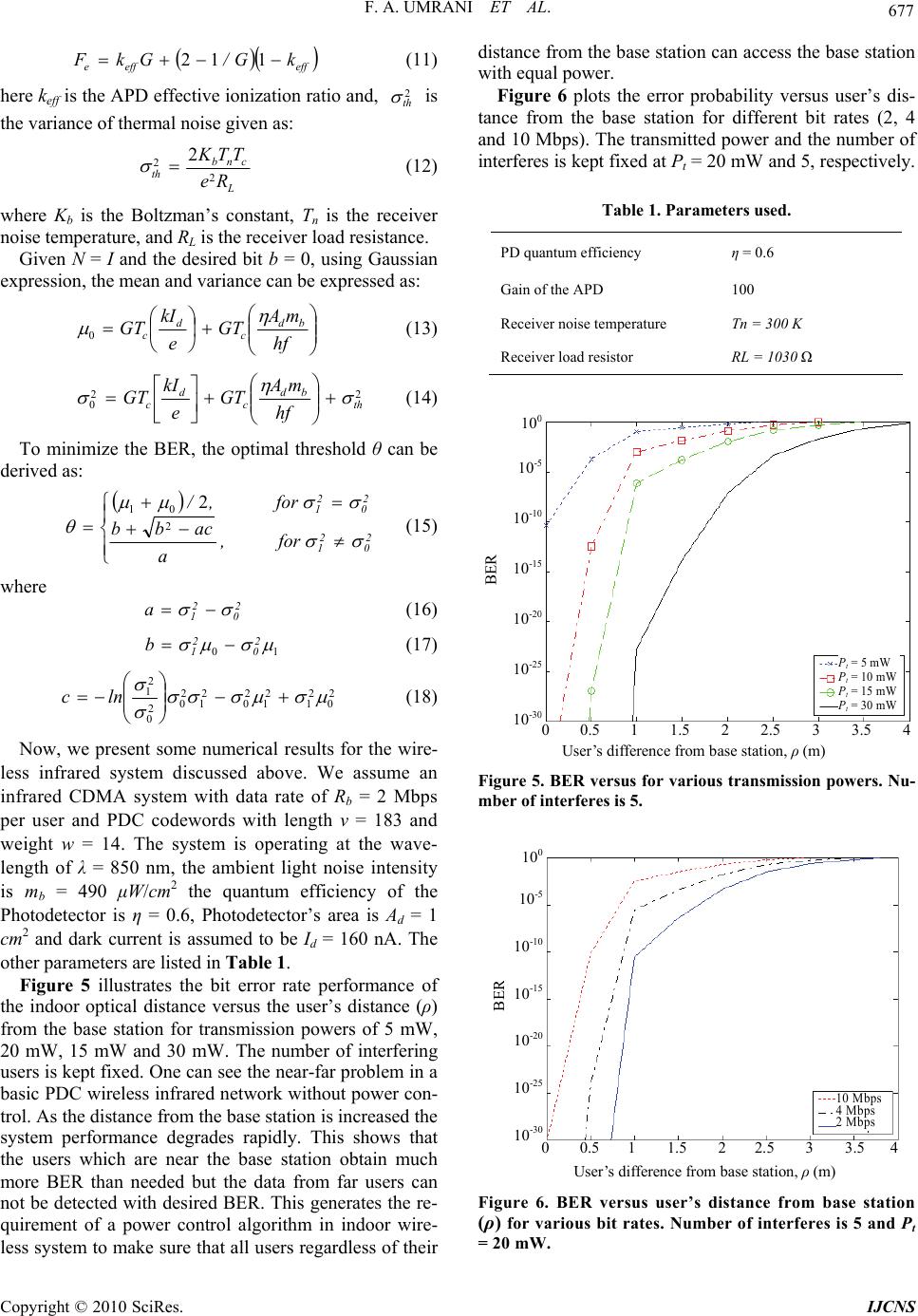

F. A. UMRANI ET AL.
677



effeffe kG/GkF  112 (11)
here keff is the APD effective ionization ratio and, 2
th

is
the variance of thermal noise given as:
L
cnb
th Re
TTK
2
22
  (12)
where Kb is the Boltzman’s constant, Tn is the receiver
noise temperature, and RL is the receiver load resistance.
Given N = I and the desired bit b = 0, using Gaussian
expression, the mean and variance can be expressed as:















hf
mA
GT
e
kI
GT bd
c
d
c


0 (13)
22
0th
bd
c
d
chf
mA
GT
e
kI
GT


 















 (14)
To minimize the BER, the optimal threshold θ can be
derived as:









2
0
2
1
2
0
2
1
for ,
a
acbb
for ,/



2
01 2
(15)
where
2
0
2
1
a


 (16)
10




2
0
2
1
b

 (17)
2
0
2
1
2
1
2
0
2
1
2
0
2
0
2
1












 lnc (18)
Now, we present some numerical results for the wire-
less infrared system discussed above. We assume an
infrared CDMA system with data rate of Rb = 2 Mbps
per user and PDC codewords with length v = 183 and
weight w = 14. The system is operating at the wave-
length of λ = 850 nm, the ambient light noise intensity
is mb = 490 μW/cm2 the quantum efficiency of the
Photodetector is η = 0.6, Photodetector’s area is Ad = 1
cm2 and dark current is assumed to be Id = 160 nA. The
other parameters are listed in Table 1.
Figure 5 illustrates the bit error rate performance of
the indoor optical distance versus the user’s distance (ρ)
from the base station for transmission powers of 5 mW,
20 mW, 15 mW and 30 mW. The number of interfering
users is kept fixed. One can see the near-far problem in a
basic PDC wireless infrared network without power con-
trol. As the distance from the base station is increased the
system performance degrades rapidly. This shows that
the users which are near the base station obtain much
more BER than needed but the data from far users can
not be detected with desired BER. This generates the re-
quirement of a power control algorithm in indoor wire-
less system to make sure that all users regardless of their
distance from the base station can access the base station
with equal power.
Figure 6 plots the error probability versus user’s dis-
tance from the base station for different bit rates (2, 4
and 10 Mbps). The transmitted power and the number of
interferes is kept fixed at Pt = 20 mW and 5, respectively.
Table 1. Parameters used.
PD quantum efficiency η = 0.6
Gain of the APD 100
Receiver noise temperature Tn = 300 K
Receiver load resistor RL = 1030 Ω
User’s difference from base station, ρ (m)
BE
R
10
0
10
-5
10
-10
10
-15
10
-20
10
-25
10
-30
0 0.5 1 1.5 2 2.5 3 3.5 4
P
t
= 5 mW
P
t
= 10 mW
P
t
= 15 mW
P
t
= 30 mW
Figure 5. BER versus for various transmission powers. Nu-
mber of interferes is 5.
User’s difference from base station, ρ (m)
BE
R
10
0
10
-5
10
-10
10
-15
10
-20
10
-25
10
-30
0 0.5 1 1.5 2 2.5 3 3.5 4
10 Mbps
4 Mbps
2 Mbps
Figure 6. BER versus user’s distance from base station
(ρ) for various bit rates. Number of interferes is 5 and Pt
= 20 mW.

678 F. A. UMRANI ET AL.
N
umber of simultaneous users
BE
R
10
0
10
-5
10
-10
10
-15
10
-20
10
-25
10
-30
5 10
15 20 25 30
20 mW
10 mW
5 mW
Figure 7. Error probability versus number of users for data
rate of 2 Mbps.
It can be seen that the path loss as the user’s move away
from the base station puts severe restrictions on the data
rate. In Figure 7, the bit error rate versus number of us-
ers is plotted. We can see that as the number of users
increase the bit error rate performance is improved. The
reason for this again can be found in Equation (7) which
shows the increase in the number of users is directly
proportional to the difference between data bit 1 and 0.
4. Summary
In this paper, we applied perfect difference codes in wire-
less domain. The uplink performance in presence of var-
ious noise sources such as path loss, ambient noise, mul-
tiple access interference and thermal noise is analyzed.
The bit error rate performance was analyzed over differ-
ent transmission powers and different data rates. It is
revealed from the results that an effective power control
algorithm is required to mitigate path loss effects.
5. Acknowledgements
This research is supported by Mehran University of En-
gineering & Technology, Pakistan.
6. References
[1] F. R. Gfeller, and U. Bapst, “Wireless in-House Data Com-
munication via Diffuse Infrared Radiation,” Proceedings
of the IEEE, Vol. 67, No. 11, 1979, pp. 1474-1486.
[2] J. R. Barry, J. M. Kahn, et al., “Simulation of Multipath
Impulse Response for Indoor Wireless Optical Channels,”
IEEE Journal on Selected Areas in Communications, Vol.
11, No. 3, 1993, pp. 367-379.
[3] J. B. Carruthers and J. M. Kahn, “Modelling of Nondi-
rected Wireless Infrared Channels,” IEEE Transactions
on Communications, Vol. 45, No. 10, 1997, pp. 1260-1268.
[4] J. M. Kahn, P. Djahani, A. G. Weisbin, K. T. Beh, A. P.
Tang and R. You, “Imaging Diversity Receivers for
High-Speed Infrared Wireless Communications,” IEEE
Communications Magazine, Vol. 36, No. 12, 1998, pp.
88-94.
[5] Z. Ghassemlooy and A. C. Boucouvalas, “Guest Editorial:
Indoor Optical Wireless Communications System and Net-
works,” International Journal of Communication Systems,
Vol. 18, No. 3, 2005, pp. 191-193.
[6] F. A. Umrani and S. Obayya, “New Encoder/Decoder
Design for Spectral Amplitude Coding Based Optical
Code Division Multiplexing (OCDM) System with Com-
mon Zero Code,” submitted for publication.
[7] X.-S. Weng and J. S. Wu, “Perfect Difference Codes for
Synchronous Fiber-Optic CDMA Communication Sys-
tems,” Journal of Lightwave Technology, Vol. 19, No. 2,
2001, pp. 186-194.
[8] M. Hall, Jr., “Combinatorial Theory,” Blaisdell Publish-
ing Company, London, 1967.
[9] H. J. Ryser, “Combinatorial Mathematics,” Wiley, New
York, 1963.
[10] T. Satoh and T. Hashimoto, “Performance Evaluation of
Chip-Synchronous, Code-Asynchronous Optical CDMA
Systems for Indoor Infrared Wireless Communications
with Diffuse Link,” Electronics and Communications in
Japan, Vol. 86, No. 4, 2002, pp. 75-88.
[11] B. M. Ghaffari, M. D. Matinfar and J. A. Salehi, “Wire-
less Optical CDMA LAN: Digital Implementation Ana-
lysis,” IEEE Journal on Selected Areas in Communica-
tions, Vol. 27, No. 9, 2009, pp. 1676-1686.
[12] S. Zahedi, J. A. Salehi and M. Nasiri-Kenari, “A Photon
Counting Approach to the Performance Analysis of In-
doors Wireless Infrared CDMA Networks,” Proceedings
of IEEE Personal, Indoor and Mobile Radio Communica-
tions, London, Vol. 2, 18-21 September 2000, pp. 928-
932.
[13] L.-L. Jau and Y.-H. Lee, “Optical Code-Division Multi-
plexing Systems Using Common-Zero Codes,” Micro-
wave and Optical Technology Letters, Vol. 39, No. 2,
2003, pp. 165-167.
[14] J. A. Salehi and C. A. Brackett, “Code Division Multiple
Access Techniques in Optical Fiber Networks–Part II:
Systems Performance Analysis,” IEEE Transactions on
Communications, Vol. 37, No. 8, 1989, pp. 834-842.
[15] A. Aminzadeh-Gohari and M. R. Pakravan, “Analysis of
Power Control for Indoor Wireless Infrared CDMA Com-
munication,” Proceedings of 25th IEEE International Per-
formance, Computing, and Communications Conference,
Phoenix, Vol. 6, 10-12 April 2006, pp. 297-302.
[16] M. Azizoglu, J. A. Salehi and Y. Li, “Optical CDMA via
Temporal Codes,” IEEE Transactions on Communica-
tions, Vol. 40, No. 7, 1992, pp. 1162-1170.