Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60803,8 pages
10.4236/jmp.2015.613202
Entanglement: A Contrarian View
A. F. Kracklauer
Independent Researcher, Weimar, Germany
Email: af.kracklauer@web.de
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 August 2015; accepted 25 October 2015; published 30 October 2015
ABSTRACT
Entanglement is defined in terms of some kind of instantaneous interaction, contrary to the relativistic principle that all interaction is possible only at a velocity less than that of light. This conflict with an otherwise inviolate principle justifies re-examination of the arguments leading to its (ostensible) rejection. Herein the historically essential notion, namely wave-collapse by measurement or the “Projection Hypothesis” of von Neumann is brought to attention and seen to violate Popper’s Principle of negatability; thereby disqualifying it as a scientific proposition. Further, it is observed that polarization of electromagnetic signals as used in experiments testing Bell Inequalities is described by structure excluding quantum principles. Consequently, most experiments taken to verify Bell’s conclusions cannot in principle do so: a quantum effect cannot be found where there is no quantum structure. Finally, a simple simulation which demonstrates the classical (electromagnetic) generation of the data that violates a Bell Inequality, thereby proving by counterexample that Bell’s so-called theorem is misunderstood, is presented.
Keywords:
Entanglement, Nonlocality, Wave Collapse, Projection Hypotheses, Q-Bit Space, EPR-B Experiments, EPR Simulations, Quantum Mechanics, Hidden Variables

1. Introduction
Entanglement was first identified by Schroedinger, who credited it with being “the distinguishing feature of Quantum Mechanics” [2] . Nowadays it is even considered as a “resource” with possible exotic but potent appli- cations. Nevertheless, it possesses several characteristics in conflict with the usual understanding and practice of both logic and lexicography. Thus, it behooves us to re-examine the historical reasons for its inclusion in physics theories, and to question whether it is in fact empirically substantiated as well as whether it is essential for theoretically explaining observed phenomena.
The first section is focused on historical issues, including speculation on the motivations for choices made at the time. The central point is that entanglement results from the application of von Neumann’s so-called “Pro- jection Hypothesis” to complex dissociated quantum systems.
In the second section, the currently popular choice of venue for experimental tests of Bell Inequalities (commonly denoted “Q-bit space”, but in fact any space with the structure group SU(2)) can be shown not to be suitable for experiments intended to plumb the structure (mysteries) of quantum mechanics.
The third section contains a discussion of the intrinsic structure of q-bit space (or electromagnetic signal polarization space) to show that its non-commutativity results from geometric structure rather than quantum dy- namics.
In the fourth section an observation first published by Edwin Jaynes, to the effect that Bell misapplied conditional probabilitites in his derivation of his famous inequalitites, thereby rendering them invalid for the intended application, is reviewed.
The fifth section discusses the largely overlooked observation that, the strategic structure of Bell’s argument requires all its inputs to be free of quantum aspects.
In the final section a fully classical (i.e., non-quantum) simulation of the prototypical experiments intended to test Bell Inequalities is described. Insofar as it is claimed that these experiments cannot be explicated without reference to either nonlocality or irreality, this simulation serves as an explicit counterexample.
In the conclusions it is noted that nothing in these arguments addresses the question of whether the heretofore regarded observable effects actually occur in nature, rather, just the character of their explanations is affected. It is seen that non mysterious and logical (in the conventional sense) principles and laws of Physics suffice.
2. Entanglement and the Projection Hypothesis
Quantum Mechanics was discovered through inspired but only partially rigorous investigations, which, however, led to impressively successful results in that eigenvalues for what turned out to be a wave equation (i.e., it has oscillatory solutions) matched up with spectral lines. On this basis, it had to be taken that this wave equation related to physical reality. At the same time, however, the eigenfunctions themselves could not be physically interpreted, a situation which launched investigations that have not been concluded to this day. Of course, nowa- days Born’s hypothesis that the squared modulus of the eigenfunctions represent probabilities of presence, inspired, perhaps by seeing similar factors in expressions for transition intensities (probabilities), is unchallenged. Nevertheless, the interpretation of at least some wave functions is problematic.
A problem arises, for example, most obviously with the so-called singlet state:
 (1)
(1)
which is taken to represent the polarization state of the light pulse pairs as emitted by sources suitable for experiments designed to test Bell Inequalities.1
Firstly, this expression, if considered as applying to a single entity (here a single pair), is a logical abomi- nation. It is the sum (negative addition) of two mutually exclusive options. It is, as it were, both black and white at once. Secondly, just this entity has never been observed “in the lab”. Although as an oxymoronic concept; this should be expected, the formal resolution of this conundrum is said to be von Neumann’s “Projection Hy- pothesis”. According to his principle, before measurement the singlet state expression is regarded as referring to the actual, observable state of the system in all its ambiguity, but at the moment of measurement, the measuring process itself causes one or the other component elements to “collapse” to an actual, ontological state for the system. This projection process is not described by Schroedinger’s equation.2
The projection process becomes additionally problematic when applied to disassociated systems. In this case, after the disassociation, the system wave function is considered still valid and ambiguous even though the component subsystems can be separated by an arbitrary space-like displacement. Thus, when one or the other component subsystem is subject to observation, it is held that the (sub) wave functions for both components, even though only one was observed, regardless of their separation, are both projected, or caused to collapse to one or the other (observable) outcome.3 This is supposed to transpire instantaneously, in contradiction to a fundamental precept of Relativity Theory according to which no interaction or communication can transpire faster than the speed of light.4
A distinct vocabulary has emerged to describe these circumstances. “Einstein causality” denotes the speed of light as the limit for interaction and communication. In addition, a term from Quantum Field Theory, namely “locality”, vice “causality”, denotes essentially the same idea; i.e., locality is respected if Einstein causality holds, which therefore precludes instantaneous action-at-a-distance, or the instantaneous transmission of force, such as thought to be the case for pre-relativistic gravity. Likewise, the state of being for a wave function before subject to an observation and the resultant collapse to a non-ambiguous, observable state, being somehow less than fully “real” (beforehand) has led to using the term “realistic” to refer to theories that do not require observers to participate in the substantiation of the universe. In other words, for theories accepting that the universe is “out there” even when no observer has been active.
Furthermore, it is common that disassociated subsystems can retain correlations from the point in time when they were associated, frequently denoted as “inherited correlation”, in which case there is no implication of a violation of Einstein causality, simply because the correlated characteristic has been carried at a subluminal velocity from the time before disassociation to a measuring station. In the case envisioned involving systems described by, for example, the singlet state, the correlated characteristic is held to be determined by an ob- servation precipitating wave function collapse in the somehow “correlated” but undetermined sub wave functions, even at a time and place for which the subsystems are separated by a space-like interval. This variant of incomplete correlation is what is denoted as “entanglement”. Clearly, it is the daughter of the Projection Hypothesis, i.e., it is exclusively the consequence of this hypothesis.
Now, the Projection Hypothesis is, from the start, suspect. It is the epitome of a non-scientific assertion in that it indisputably satisfies Popper’s criterion, namely, that any proposition that cannot be negated in principle, is inadmissible in science. In this case it is self evidently true that it is impossible to verify without observation that before observation an ambiguous state prevailed. Thus, it can be asked: is there a modification of the total quan- tum paradigm precluding these soft, ancillary, essentially lexicographical aspects of Quantum Theory? Perhaps.
Suppose, at the start, that it is taken that, the expression for the singlet state, Equation (1), does not pertain to a single system, but rather incorporates features characterizing the statistics of an ensemble of systems, each element of which is either one or the other of the two component systems comprising the singlet state. That is to say that, the singlet state is an average of the actual ensemble of the two component states although it itself is not a member of the ensemble, which however, for calculating certain statistical properties of the ensemble, suffices. Further, let us suppose that whatever characteristics disassociated subsystems retain are embedded in them before disassociation and are simply transmitted to measuring stations from a common origin. All correlated aspects are described with standard, statistical techniques; there is no need for preternatural “entangle- ment”. Thus, upon measurement, there is also no need for hypotheses regarding wave function collapse, or reason for doubting the existence of a “real world” independent of observer participation. This viewpoint, of course, is exactly that championed by Einstein throughout his life. His view holds that Quantum Theory is incomplete, i.e., a statistical theory for averages of ensembles of identical entities but not a theory of individual entities [3] .
3. A Structural Issue Vexing Experiment
In the very early days of the development of Quantum Theory when it was noticed by Einstein, Podolsky and Rosen (EPR) that the interpretation of quantum wave functions was ambiguous, even undetermined, they proposed a Gedanken experiment to illustrate the problem. It involved considering the mechanical disintegration of an object into two identical parts moving away from each other. They pointed out that, in effect, for this situation, one could measure the position of one daughter, the momentum of the other, and in view of symmetry, then specify both variables for both daughters precisely. From this they drew the conclusion that, Quantum Mechanics, which precludes the precise determination of both, was not a fundamental theory, deeper than Classical Mechanics, but rather an elaboration of Statistical Mechanics. In other words, Quantum Mechanics is incomplete and the search for a deeper, mechanical theory would be in order.
Gedanken experiments alone are not considered valid science. However, the arrangement envisioned by Einstein et al. for a real experiment would be practically unrealisable. It was only after Bohm suggested a change of venue that serious experimental efforts were undertaken. Unfortunately, Bohm’s proposal is con- ceptually flawed.
The EPR setup envisions analysis in phase space, in other words in terms of the variables “position” and “momentum”. In mechanical terms, these two variables are classified as “Hamiltonian conjugates”. Quantum Theory employs these variables and, among other things, specifies by means of the Heisenberg Uncertainty Relationship that both of these variables cannot be arbitrarily precisely determined simultaneously. So much is very well known. But, on the other hand, the venue proposed by Bohm is in fact what is nowadays denoted “Q-bit” space. This space is spanned by two vectors; in Bohm’s application they are the two vectors used to describe the two states of polarization of electromagnetic signals, e.g., vertical and horizontal (or right, left circular). They are not Hamiltonian conjugates; there is no reason that in principle they cannot be determined to arbitrary precision. In brief, Q-bit space is neither “quantized” nor “quantizable” [4] .
It is true that the vectors spanning Q-bit space are non-commutative, as are quantized phase space variables; but, in this case non-commutivity is a consequence of geometry and not imposed by special mechanical- dyna- mical requirements. This insight can be strengthened by recalling that group structure of Q-bit space, SU(2), is homeomorphic to the group of rotations on a sphere, SO(3). The non-commutivity of the latter group is obviously geometric and not dynamical in character. Because of the homomorphism, the non-commutivity of SU(2) must have the same foundation: geometry.
The consequence of the true group structure of Q-bit space is that there is no quantum structure there to investigate experimentally. Thus, that the experiments performed in this venue are held to verify that Quantum Mechanics implies that the reality is nonlocal, is simply mistaken.
4. A Structural Issue Vexing Theory
On the basis of the conclusions in the previous section, one might tend to conclude that, in the venue for the experiments in view of the validity of the results obtained by Bell, the remedy is just to more carefully choose an appropriate venue. In this section an argument is presented that this conclusion is also defective.
The basic criticism of this sort, apparently published first by Edwin Jaynes, is that in developing his argument, Bell was mislead by using improper notation [5] . The consequence was that the algebraic manipulations used to extract his famed inequalities are valid only for a restricted case, namely when the two daughter products of EPR events have a correlation coefficient of “0”, contrary to the initial hypothetical input into his argument.
The error involved is due to Bell’s expression for probabilities (as given by the ratio of the number of detections per the number of repetitions of the experiment) for optical pulses passing polarisers with various axial angles at each measurement station, namely as  and
and , where
, where  are polariser axial angles and
are polariser axial angles and 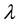 represents whatever additional variables are needed to fix outcomes deter- ministically. These two symbols, A and B, appear to have symmetric structure in Bell’s calculations.5 The polariser settings pertain to passive action, they filter impinging pulses and respond only when they have suit- able polarization as fixed at their inception―no non-local realization process need be involved.
represents whatever additional variables are needed to fix outcomes deter- ministically. These two symbols, A and B, appear to have symmetric structure in Bell’s calculations.5 The polariser settings pertain to passive action, they filter impinging pulses and respond only when they have suit- able polarization as fixed at their inception―no non-local realization process need be involved.
While these expressions are indeed probabilities, in Bell’s application they cannot both be absolute pro- babilities; rather, one of them must be a conditional probability if they are to pertain to correlated events as presumed in the hypothetical input into the derivation of Bell Inequalities. As a matter of precise expression, they are best written in the customary notation as, e.g.,  and
and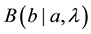 , that is, in accord with Baye’s formulas (AKA: the chain rule) for correlated events. In particular, the expression for a joint probability for correlated events must be of the form:
, that is, in accord with Baye’s formulas (AKA: the chain rule) for correlated events. In particular, the expression for a joint probability for correlated events must be of the form:
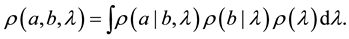 (2)
(2)
In fact, however, Bell wrote:
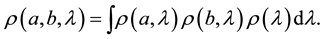 (3)
(3)
The formally correct mode of expression or notation makes it clear from the start that these two terms are not symmetric in formulation and cannot mindlessly be manipulated algebraically as if they were. In fact, when this structure is taken into account correctly, the derivation of inequalities is stymied, it does not go through. Note, however, that when the correlation coefficient is zero, or the outcomes are uncorrelated (i.e., it is a special case), they are then symmetric, the derivation of the inequalities does goes through and the outcome is valid. It is not relevant, however, for the proposed experiments regardless of their experimental venue.
5. A Meta Issue Vexing Reasoning
The fundamental question addressed by Bell’s considerations is the question: is Quantum Theory complete? In other terms this question can be formulated as: does there exist a meta theory with additional variables which both evades the troubling aspects of Quantum Theory as originally formulated and which when averaged over the additional extra variables projects back to the current Quantum Theory?6 It was, as is well known, EPR’s intention to provide a proof that Quantum Theory is in fact incomplete.
It was Bell’s intention to test their proof by counter argument, that is by seeking an empirically decidable statement based on the implicit assumption that there does exist a theory with additional variables, i.e., a meta theory, which when averaged over the additional variables yields without contradictions the original or current version of Quantum Theory. At the meta theory level he proposed consideration of certain formula, principally the definition of a joint probability, as discussed in the previous section. The point here, however, is that, at the meta level all reasoning and calculations are by hypothesis free of the ambiguous or weird aspects known in nowadays conventional Quantum Theory. Thus, all argumentation and computations at this level must rigorously avoid all quantum structure. All the mathematics, especially statistical analysis, must be taken from conventional, non quantum sources. Much analysis pertaining to Bell Inequalities, or the questions they are intended to address, however, fails to respect this assumption. The result of this oversight is often vastly misleading; its looks erudite when in fact it is gratuitous [7] .
6. EPR Simulation: A Counter Example
For a long time already critics of entanglement, nonlocality and the like, have pointed out that, there exists various classical phenomena exhibiting exactly the same correlations as are calculated using quantum algorithms. Many of these same critics employ calculations using non-quantum, or standard statistical means, but still get the result predicted by Quantum Mechanics. A straightforward understanding of the consequences of Bell's analysis is that an understanding of the observed results from EPR-type experiments cannot be understood outside of Quantum Theory. That is to say that, the results of these experiments cannot be obtained from macroscopic set-ups or models thereof. This conflict has been under study by a small number of researchers for decades, but the results seem to have been unconvincing. There are at least two possible reasons, one: the classical models have all been of bulk effects and not of event-by-event processes similar to the presumed photon-by-photon detections ostensibly observed in experiments at the atomic level; and two: the expressions for correlation coefficients discussed in connection with the analysis of data from atomic level experiments as analysed using quantum methods cannot be used for the analysis of data from macroscopic phenomena without attention to the requirement for zero-mean data.
In the following a macroscopic, i.e., classical, model of EPR processes is described which provides data violating a Bell Inequality when analysed rigorously respecting the formal definition of a correlation coefficient. Such a simulation serves as a counter-example to the claim that EPR correlations cannot be understood outside the context of quantum theory, in particular without nonlocal interaction. While many various classically com- prehensible phenomena have been presented in the literature, the one which is the closest to the vast majority of experiments, namely EPR-B optical experiments, is that proposed by Misrahi and Moussa [8] .
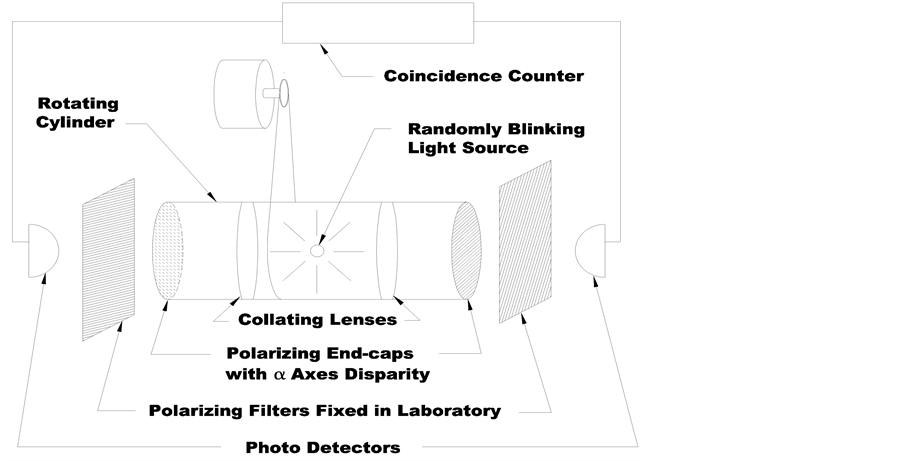
These authors discuss both the fabrication of a macroscopic set-up and the analysis of a simulation, but do the calculations in terms of measurements of the detected signal intensity in units of volts. Thus, their discussion deviates from the experiments done an the microscopic level at which the data is strictly detection counts, or the detection of a signal: “yes” or “no” per the number of trials. Thus, their presentation appears to have been found to be unconvincing and is largely ignored. We aim here to remedy the situation by extending the simulation to an event-by-event simulation in which the intensity of a detection is revealed by the ratio of detections per trials as determined by Malus’ Law. See Figure 1.
Our simulation of this experiment at an event-by-event level is accomplished in four blocks [9] . The first block randomly, but evenly, selects the pair of orientations for the analytical polarisers. For the calculation of a Bell Inequality (of the CSHS version), a set of four terms, each representing the average detected rate for a particular selection of angles, is needed.
Because it has been suggested that there could exist some kind of interaction between the measuring stations, the experiments have been constructed to randomly select the two angles from the set of four possible com- binations between the time the signals have been generated and their arrival at measuring stations. If this selection occurs at a time less than the time taken by light to travel between the stations, then it can be considered confidently that the state of either measuring station has not been altered as a result of the outcome at the other station, i.e., conspiratorial collaboration has been precluded. Simulations have traditionally modelled this feature although it is strictly superfluous when the conspiratorial collaboration itself has not been built into the simulation code beforehand. The first block of code in our simulation respects this tradition, albeit po- intlessly.
The second block of code simulates the generation of the correlated pulses. The fact that the polarisers mounted on the ends of the rotating cylinder depicted in Figure 1 have polarization axes fixed with respect to each other satisfies this stipulation. In addition, the pairs of signals are given by means of randomly timed flashes within the rotating cylinder, thereby simulating the random orientation of the pairs singly as naturally generated in experiments. This random bias angle makes the individual detection probabilities fully random at each station when taken individually.
In the third block detections are simulated by comparing the square of the cosine of the difference in the measuring orientation angles generated in the first and the polarization orientations of the simulated pulses generated in the second block with a random number. This comparison is made on the basis of Malus’ Law. Finally the quantity of positive coincidences, which are the only manifestation of real experimental pulses available for laboratory experimentation, are counted.
Figure 1. Schematic of a macroscopic EPR-B experiment as proposed by Misrahi and Moussa.
Block Four comprises 1) data normalization, 2) a shift to zero-mean (as required for use in the definition of a correlation coefficient
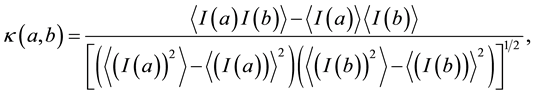 (4)
(4)
and 3) computation of the Bell Inequality
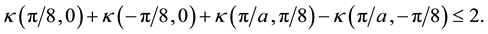 (5)
(5)
The angular choices in Equation (5) give a maximum violation of 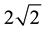 in principle. The simulation gives values scattered about this maximum. From the construction of the simulation it is obvious that the number of detections at each station is determined only by the local polariser setting and the local polarization of the signal impulse. Of course, the pulses are correlated as generated at their source and that “hereditary” correlation is carried to the measurement stations. No preternatural interaction between stations is involved, thereby demon- strating by counter example that Bell’s claim is incorrect: proof of nonlocality in Nature by means of entangle- ment has not been found.
in principle. The simulation gives values scattered about this maximum. From the construction of the simulation it is obvious that the number of detections at each station is determined only by the local polariser setting and the local polarization of the signal impulse. Of course, the pulses are correlated as generated at their source and that “hereditary” correlation is carried to the measurement stations. No preternatural interaction between stations is involved, thereby demon- strating by counter example that Bell’s claim is incorrect: proof of nonlocality in Nature by means of entangle- ment has not been found.
Many, perhaps all, previous simulations have encountered a difficulty that the requirement for zero-mean data was overlooked. In order to obtain the expected results, it appears that for the analysis of the data for those simulations (as well as for various experiments) one of the channels was labelled “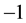 ” and the calculations were done with the labels. This would be an artificial tactic. In the quantum calculation this aspect is covered by the normalization and minus sign found in the definition of the singlet state.
” and the calculations were done with the labels. This would be an artificial tactic. In the quantum calculation this aspect is covered by the normalization and minus sign found in the definition of the singlet state.
7. Conclusions
Herein arguments have been presented to the effect that the preternatural character ascribed nowadays to electromagnetic interaction (as mediated ostensibly by photons), especially entanglement, results from the application of principles that can be challenged. It seems that the ultimate cost of abandoning the inclusion of the concept of entanglement would be to focus instead on the well founded notion of hereditary statistical correlation. The resulting benefits include a clear and intuitive explanation of the relevant physical effects, a circumstance which would have, at a minimum, great pedagogical advantage.
It is interesting to speculate on the historical and psychological factors that led in the first instance to the tolerance of more or less blatantly counter-intuitive, if not even illogical, thought complexes. Certainly one factor that was the development of Quantum Theory was undertaken as, and thought of as, a refinement of Mechanics and not of Statistical Mechanics or Thermodynamics. The founding fathers, as it were, apparently considered themselves involved in the development of a deeper form of mechanics pertaining to individual systems rather than to ensembles of systems. This conviction, evidently led them to reduce their threshold for far fetched explications, without doubt including the obviously unscientific “Projection Hypothesis”, which offered a way to consider a probability density as the ontological expression of an individual physical, concrete entity. From this one step follow most of the artificial contrivances involved in interpreting quantum effects.
Likewise the inadmissible identification of Q-bit space (or any mathematical space for which the group SU(2) specifies structure) as functionally equivalent to phase space seems to be a consequence of the fact that in certain applications, in particular to spin, the vectors spanning the space have an amplitude proportional to Planck’s reduced constant, . This circumstance is irrelevant, however, to the structure pertaining to the interrelationship of the two independent vectors spanning the space. Q-bit, or polarization space is simply not spanned by Hamiltonian conjugates no matter how its basis vectors are scaled in the spins case by some multiple of
. This circumstance is irrelevant, however, to the structure pertaining to the interrelationship of the two independent vectors spanning the space. Q-bit, or polarization space is simply not spanned by Hamiltonian conjugates no matter how its basis vectors are scaled in the spins case by some multiple of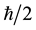 , but not in the case of polarization of electromagnetic signals.
, but not in the case of polarization of electromagnetic signals.
Difficulties of finding an event-by-event simulation of an experiment testing a Bell Inequality can be attributed, perhaps to the fact that the definition of a correlation coefficient requires the data to be in a zero- mean form. This requirement is not discussed explicitly in the literature describing EPR experiments. When, nevertheless, this requirement has been satisfied, it appears that this is the inadvertent consequence of labelling one of the measurement stations with “
Finally, the general understanding of the implicit strategy of Bell’s investigations has been overlooked by Bell himself even. The fundamental purpose of his researches into Quantum Theory was to answer the question: does there exist a covering or meta theory free of the troublesome, often weird, features? Such a meta theory would of necessity involve additional variables, which are absent (hidden) at the current level. To formally examine this question, Bell implicitly hypothesizes that such a meta level exists, and then he asks what reflection its existence might have on the lower, current level of Quantum Theory. Given that by assumping the meta level is to be free of all non standard structure, all calculations done and definitions used at that level must conform with pre-quantum science and mathematics, a proscription often honoured in the breach.
In summary, the evidence for entanglement being something other than ordinary hereditary correlation is profoundly questionable. For certain, evidence for non-locality is totally dependant on unorthodox mathematical argumentation, not direct observation―nothing going faster than light has been observed, just the violation of an informally formulated inequality for which the rectitude of its interpretation is not beyond challenge.
Cite this paper
A. F.Kracklauer, (2015) Entanglement: A Contrarian View. Journal of Modern Physics,06,1961-1968. doi: 10.4236/jmp.2015.613202
References
- 1. Greenstein, G. and Zajonc, A.G. (1997) The Quantum Challenge. Jones and Bartlett Publishers, Sudbury.
- 2. Schroedinger, E. (1935) Die gegenwärtige Situation in der Quantenmechanik (The Present Situation in Quantum Mechanics). Naturwissenschaften, 23, 887-812.
- 3. Einstein, A. (1948) Quantum Mechanics and Reality. Dialectica, 2, 320-324.
http://dx.doi.org/10.1111/j.1746-8361.1948.tb00704.x - 4. Kracklauer, A.F. (2002) Is Entanglement Always Entangled? Journal of Optics B: Quantum and Semiclassical Optics, 4, S121-S126.
- 5. Jaynes, E.T. (1989) Clearing up Mysteries: The Original Goal. In: Skilling, J., Ed., Maximum Entropy and Baysian Methods, Kluwer Academic Press, Dordrecht, 1-27.
- 6. Kracklauer, A.F. (2006) What’s Wrong with This Rebuttal. Foundations of Physics Letters, 19, 625-629.
http://dx.doi.org/10.1007/s10702-006-1016-3 - 7. Kracklauer, A.F. (2007) Bell's Ansatz and Probability. Optics and Spectroscopy, 108, 451-458.
http://dx.doi.org/10.1134/S0030400X07090147 - 8. Misrahi, S.S. and Moussa, M.H.Y. (1993) Einstein-Podolsky-Rosen Correlations for Light Polarization. International Journal of Modern Physics B, 7, 1321-1330.
http://dx.doi.org/10.1142/S0217979293002341 - 9. Kracklauer, A.F. (2015) What Is a Photon? Proc. of SPIE 9570, No. 21.
NOTES
1Although not essential for the point made here, for an accessible presentation of both the Quantum Theory and use of the singlet state see Ref: [1] .
2Although nowadays this concept is credited to von Neumann, who in 1932 published extensive mathematical analysis of it, the basic concept appears to have been introduced publicly first by Einstein at the Solvey Conference in 1927. There he pointed out that a particle beam represented by a wave function upon passing through a pin hole would diverge as a semicircular wave and impinge on a semicircular detector centered on the pin hole over its whole inner surface at once. Nevertheless, the detector would in fact respond by emitting flashes at distinct points corresponding to individual beam particles. Einstein pointed out that this requires that the beam’s wave function, finite over the whole detector, must have collapsed instantly to the flash points by means of a process alien to quantum theory.
3Although determining both values by measurement is problematic, determining one by measurement and then the other by symmetry or a conservation principle is straightforward.
4Arguments that insofar as this effect cannot be used for human communication, it does not violate Einstein causality are too facile. Einstein causality does not restrict just communication, or just human workings, but every interaction.
5In addition, these symbols are complicated by the fact that they stand for sequences of measurement results-not just single terms [6] .
6Insofar as the envisioned extra variables are unknown at present, they are customarily referred to as “hidden” variables.