Applied Mathematics
Vol.06 No.08(2015), Article ID:58453,18 pages
10.4236/am.2015.68132
Universality in Statistical Measures of Trajectories in Classical Billiard Systems
Jean-François Laprise, Ahmad Hosseinizadeh, Helmut Kröger
Department of Physics, Laval University, Québec, Canada
Email: jean-francois.laprise@crchudequebec.ulaval.ca, hosseina@uwm.edu, helmut.kroger@phy.ulaval.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 January 2015; accepted 27 July 2015; published 30 July 2015
ABSTRACT
For classical billiards, we suggest that a matrix of action or length of trajectories in conjunction with statistical measures, level spacing distribution and spectral rigidity, can be used to distinguish chaotic from integrable systems. As examples of 2D chaotic billiards, we considered the Bunimovich stadium billiard and the Sinai billiard. In the level spacing distribution and spectral rigidity, we found GOE behaviour consistent with predictions from random matrix theory. We studied transport properties and computed a diffusion coefficient. For the Sinai billiard, we found normal diffusion, while the stadium billiard showed anomalous diffusion behaviour. As example of a 2D integrable billiard, we considered the rectangular billiard. We found very rigid behaviour with strongly correlated spectra similar to a Dirac comb. These findings present numerical evidence for universality in level spacing fluctuations to hold in classically integrable systems and in classically fully chaotic systems.
Keywords:
Classical Chaos, Dynamical Billiards, Random Matrix Theory, Level Spacing Fluctuations, Universality

1. Introduction
The idea to model apparently disordered spectra, like those of heavy nuclei, using random matrices was sug- gested in the mid-50’s by Wigner, and then formalized in the early 60’s in the work of Dyson and Mehta [1] -[6] . They showed that random matrices of Gaussian orthogonal ensembles (GOE) generate a Wigner-type nearest- neighbour level spacing (NNS) distribution [6] . In a seminal paper, Bohigas, Giannoni and Schmit (BGS) for- mulated a conjecture [7] stating that time-reversal invariant quantum systems with classically fully chaotic (ergodic) counterpart have universality properties given by random matrix theory (RMT). Experiments in nu- clear physics, for example, have shown that spectra originating from different heavy nuclei give the same Wignerian energy level spacing distribution [8] . Universality properties in quantum chaos of bound systems, i.e. quantum systems with a fully chaotic classical counterpart, have now been demonstrated in many experiments, computational models and in theoretical studies [6] [9] -[14] . Theoretical support of the BGS conjecture came from the semiclassical theory of spectral rigidity by Berry [15] [16] , who showed that universal behaviour in the energy level statistics is due to long classical orbits. Sieber and Richter [17] investigated the role of correlations between classical orbits. The semiclassical theory has been further developed by Müller et al. [18] [19] . In ref. [19] they presented the “core of a proof” of the BGS conjecture, which, by proving arguments previously used by Berry [15] , show that in the semi-classical limit the periodic classical orbits determine the universal fluctua- tions of quantum energy levels. Further refinements have been made by Keating and Müller [20] .
The study of classical strongly chaotic systems (Anosov systems) has revealed that central limit theorems (CLT) hold [21] -[26] . This has been proven for the 2D periodic Lorentz gas with finite horizon. The first step of a proof was given by Bunimovich and Sinai [21] and was completed by Bunimovich, Sinai and Chernov [23] . At macroscopic times, such deterministic chaotic system converges to Brownian motion, i.e. behaves like a random system [21] [23] [24] [26] . This is also supported by the existence of an average diffusion coefficient [21] [23] [27] , showing the diffusive character of such chaotic system.
Do classical fully chaotic systems also exhibit universality properties? This question was addressed by Argaman et al. [28] , who showed that there is universal behaviour in 2 points correlation functions of actions of periodic orbits of classically chaotic systems. As examples they considered the deformed cat-map and the baker-map. This has been elaborated further in a number of studies by Dittes et al. [29] , Aurich and Sieber [30] , Cohen et al. [31] , Tanner [32] , Sano [33] , Primack and Smilansky [34] , Sieber and Richter [17] and Smi- lansky and Verdene [35] . Argaman et al. started from the assumption that spectral fluctuations of chaotic quantum systems follow the predictions of RMT and they derived a universal expression for classical cor- relation functions of periodic orbits via Gutzwiller’s semi-classical trace formula. They concluded “The real challenge, though, is to find out whether these action correlations can be explained on a completely classical level”.
An answer was proposed by Laprise et al. [36] [37] who found universal behaviour in classical 2D billiards by looking at fluctuations in spectra of classical action/length matrices from billiard trajectories. They showed that one could distinguish chaos from integrability in classical systems using RMT and an analogue of the BGS- conjecture. In particular, they considered the Limaçon/Robnik family of billiards, which interpolates between the chaotic cardiod billiard and the integrable circular billiard. For the cardioid billiard, the level spacing dis- tribution 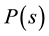 and spectral rigidity
and spectral rigidity 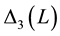 were found to be consistent with the GOE behaviour predicted by RMT. For the interpolating case close to the circle, the behaviour approached a Poissonian distribution. The circular billiard itself was found to be very rigid and strongly correlated and yielded
were found to be consistent with the GOE behaviour predicted by RMT. For the interpolating case close to the circle, the behaviour approached a Poissonian distribution. The circular billiard itself was found to be very rigid and strongly correlated and yielded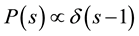 . The jump in behaviour at the transition to the circle is associated with the corresponding change in the symmetry group.
. The jump in behaviour at the transition to the circle is associated with the corresponding change in the symmetry group.
This article extends the results of reference [36] in the following directions: 1) We consider the 2D rec- tangular billiard as another example of an integrable billiard. Compared to the circular billiard, this billiard has lower symmetry (no group property). Nevertheless, it displays strong spectral correlation and rigidity like the circular billiard. 2) We present numerical studies for other chaotic 2D billiards: the Sinai-billiard and the Bunimovich stadium billiard. 3) In order to understand the observed universal behaviour in chaotic billiards, we present arguments linking such behaviour to CLTs, diffusive and random walk behaviour. In particular, we present a mathematically rigorous result on the distribution of length of trajectories.
The answers we found can be summarized as follows: For the 2D Sinai billiard and the 2D Bunimovich stadium billiard the level spacing distribution 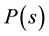 and spectral rigidity
and spectral rigidity 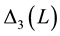 are consistent with pre- dictions of RMT (GOE behaviour), i.e. show universal behaviour. This behaviour is statistically the same as the one observed in quantum chaos (obtained from energy level spacing distributions). The implication of these findings is that RMT not only represents well the statistical fluctuation properties of the energy spectrum of chaotic quantum systems, but also those of the length spectrum of chaotic classical systems. Moreover, sta- tistical fluctuations obtained from spectra of action/length matrices clearly distinguish chaotic from integrable systems.
are consistent with pre- dictions of RMT (GOE behaviour), i.e. show universal behaviour. This behaviour is statistically the same as the one observed in quantum chaos (obtained from energy level spacing distributions). The implication of these findings is that RMT not only represents well the statistical fluctuation properties of the energy spectrum of chaotic quantum systems, but also those of the length spectrum of chaotic classical systems. Moreover, sta- tistical fluctuations obtained from spectra of action/length matrices clearly distinguish chaotic from integrable systems.
2. Length and Action of Trajectories
In classical systems, chaos information is encoded in trajectories. According to the Alekseev-Brudno theorem [38] the temporal length t is related via the Kolmogorov-Sinai K entropy to the information 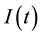 in the segment of trajectory,
in the segment of trajectory,
 (1)
(1)
This motivates us to look at the length of trajectories and its fluctuation properties. Let 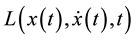 denote the Lagrangian of a system, let
denote the Lagrangian of a system, let 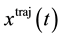 denote a solution (trajectory) of the Euler-Lagrange equations, with boundary points
denote a solution (trajectory) of the Euler-Lagrange equations, with boundary points 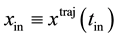 and
and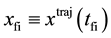 . Let
. Let
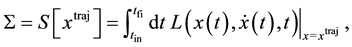 (2)
(2)
denote the action over 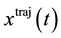 and let
and let
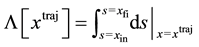 (3)
(3)
denote the length of the trajectory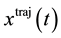 . We choose a finite set of discrete points
. We choose a finite set of discrete points . For all pairs of boundary points
. For all pairs of boundary points


where i and j are respectively the indices of the final and initial boundary points of the trajectory. Both matrices are viable for statistical analysis of classical chaos. In the case of billiard systems, we consider trajectories where the billiard particle moves with constant velocity u and constant kinetic energy E. Then the action and the length matrix are essentially equivalent,

Numerical Calculation of Length Matrices
When solving for two boundary points 



For 





range

the number of trajectories and retaining only the trajectories corresponding to the starting angles

3. Integrable Billiard
If one considers integrable quantum systems and analyzes them in terms of the NNS distribution of energy levels and spectral rigidity, then in most cases one finds a Poissonian distribution 


spectral rigidity 


were found in the case with weak harmonic coupling, yielding 


Laprise et al. [36] considered the classical integrable circular billiard and constructed a length matrix from classical trajectories between boundary points located evenly on the billiard wall. They found saturation in the spectral rigidity for large L at 



Rectangular Billiard
As example of an integrable classical billiard we consider the 2D rectangular billiard, shown in Figure 1.
The shape is determined by the parameters a, b, which were chosen to be 



For a given pair of boundary points, we found that the behaviour of the number of trajectories versus the number of rebounds is linear (not shown). The error behaviour of trajectories as a function of the number of rebounds has been obtained by taking into account 


The symmetry of the rectangular billiard is mirror symmetry under reflection about the x- and y-axes (with origin at centre of rectangle). The symmetry shows up in the shape of trajectories. For example, a trajectory (1) going from starting point 



Figure 1. 2D Rectangular billiard. Horizontal length a, vertical length b. Trajectories go from boundary points 

group of discrete translations,” which imply strong correlations among length matrix elements and among eigenvalues of the length matrix. We expect that this will manifest itself in the statistical behaviour in the level spacing distribution 







computed the correlation coefficient to obtain


This is possibly evidence for universal behaviour in the integrable case. Comparing the behaviour of the rectangular billiard with the circular billiard [36] , we observe that they differ in their symmetry properties. In the circular billiard hopping from one boundary point to its neighbour stands for a group operation. The corre- sponding operation in the rectangular billiard has no group property. However, the resulting strong correlation and spectral rigidity are found to be very similar for both billiards.



Figure 2. Rectangular billiard. (a) Distribution of length matrix elements


4. Chaotic Billiards
4.1. Sinai Billiard
For general closed 2D billiards, the mean free path length 

where 





The rule of dynamics is free motion in the interior region and elastic specular collision at the central disc and the exterior square wall. We have classified trajectories using the scheme presented in Section 2. A global


Figure 3. (a) Geometry of 2D Sinai billiard (not to scale). Para- meters: radius of sphere



characteristic feature of chaos is encoded in the number of classical trajectories. For the Sinai billiard we found that the number 


Such exponential behaviour in chaotic billiards is clearly distinct from the behaviour in integrable billiards, where the number of trajectories increases linearly with the number of rebounds (see rectangular billiard). We
fixed a value for 

to all possible trajectory indices

In order to make sure that the chaotic behaviour is not due to numerical noise, we estimated the numerical error 






For 
We found a relative error of about 














The histogram of the length matrix elements itself is shown in Figure 4(a). The distribution looks close to a Gaussian. Determining if it is a pure Gaussian, is a question physically relevant for the following reason: If the distribution 




Mathematical note. The BGS-conjecture does not state that the matrix elements of a quantum Hamiltonian must be distributed like a GOE ensemble. The conjecture rather only says that the statistical fluctuations of the eigenvalue spacings obtained from the quantum Hamiltonian are the same as those from a GOE ensemble, giving a Wignerian distribution. In other words, it is possible that the matrix elements of the quantum Hamil- tonian be distributed quite differently from a Gaussian and that its level spacing distribution be nevertheless Wignerian.


Figure 4. 2D Sinai billiard.


Such a situation, where the distribution of matrix elements is not GOE, but the level fluctuation statistics is GOE, occurs in nuclear physics. An example is the distribution of the Hamiltonian matrix elements obtained from nuclear shell model calculations [12] . In this model, there are vanishing Hamiltonian matrix elements. This implies that the number of independent matrix elements is much smaller than in a random matrix of the same size. However, Brody et al. [47] showed that the 2-body residual interaction in the shell model yields matrix elements of random character following a Gaussian distribution. In particular, they showed that spectral fluctuation properties from such ensembles with orthogonal symmetry are identical to those from GOE. That implies that GOE is meaningful to predict spectral fluctuation properties of nuclei governed by 2-body interactions, though the Hamiltanian does not follow a Gaussian distribution.
4.2. Bunimovich Stadium Billiard
Let us consider the 2D Bunimovich stadium billiard with semi-axes a and b (Figure 5). The billiard is known to be fully chaotic [48] [49] . The billiard is symmetric under mirror operation about x- and y-axes. In order not to mix different symmetry classes, we consider the billiard with boundary points 



The rule of dynamics is free motion in the interior region and elastic specular collision at the exterior square wall. For a given pair of boundary points, the number of trajectories 

Such behaviour is qualitatively similar to that found in the Sinai billiard. We also measured the numerical
Figure 5. 2D stadium billiard. Trajectories go from boundary points 

error following the method used in the Sinai billiard. Likewise, we found a regime of exponential behaviour followed by a regime of saturation (not shown). On average the exponential increase is given by

We have classified trajectories by the the number of rebounds
generate an ensemble of length matrices 

For each trajectory index 




In order to see if the observed Wigner distribution in the level spacing distribution depends on the statistical method of averaging over several trajectories (i.e. length matrices
5. Universality in Chaotic Billiards
The numerical experiments with chaotic billiards investigated above led us to the following observations: 1) For a given pair of boundary points










The leading Gaussian behaviour in the distribtion 




Figure 6. 2D stadium billiard. Average over trajectories. Geometry parameters








discs. There are two types of 2D periodic Lorentz gases (or Sinai billiards on a torus): One has a finite horizon, where free paths between collisions are bounded (the scatterers are sufficiently dense to block every direction of motion. The other type has an infinite horizon, where the particle can move indefinitely without collision with



Figure 7. 2D stadium billiard. Average over shapes of stadium. (a) Distribution of length matrix elements.


any disc. The Sinai billiard investigated above (see Figure 3(a)) belongs to this class. The CLT, the existence of finite diffusion coefficient and the convergence to Brownian motion were proven only for the periodic Lorentz gas with finite horizon [21] [23] . In the case of infinite horizon, the CLT has not been proven. Moreover, in this case the diffusion coefficient is infinite and there is no convergence to Brownian motion [51] .
Actually, for the periodic Lorentz gas with finite horizon it can be shown rigorously that the distribution of length of trajectories becomes a Gaussian distribution in the limit of many bounces. This holds when the initial points of trajectories are distributed randomly on the billiard boundary. Then Chernov and Markarian [52] prove the following result

for all


is the time of the n-th collision. 





This result seems to support our numerical findings of a (near) Gaussian distribution of length of trajectories. However, the scenario where the above mathematical result holds and the scenario of our numerical study differ in two respects, namely in the distribution of boundary points and in the horizon of billiard. For the purpose of statistical analysis in terms of RMT we are interested in the distribution


In the case of the stadium billiard, Bálint and Gouëzel [53] have shown that a limit theorem also holds. They proved that the limit distribution 



Let us suppose that 




Now we want to address the following questions:
1) Concerning universality observed in classical chaotic billiards, what are the underlying physical principles? We will give a heuristic description-not a rigorous derivation-of the physical principles leading to the pheno- menon of universality. Let us consider chaotic billiards in the regime of macroscopic times, i.e., when the billiard particle does a large number of bounces. Consider a trajectory carrying out 







2) What is the physical significance of such universality? If one considers classically chaotic billiards in the regime of macroscopic times, where 











3) Are there connections between universality and physical quantities which are easily observed in real systems? In particular, is such universality related to transport properties of the classical system? The answer is yes, and we will show in Section 6 how a transport coefficient can be obtained from the length matrix 
Moreover, the behaviour of the chaotic billiard systems when approaching the regime of universality is characterized by laws specific for the particular billiard system. As example consider the decay laws of correla- tion functions. Consider a billiard trajectory and consider as observable f the segment of trajectory from n to



or polynomial fall off behaviour

where A and B are constants, 

Here we suggest for chaotic billiard systems that the approach towards universality (i.e., increasing the number of rebounds) contains further physical information characteristic for the system. In particular, we expect that the distribution 

for
4) Are those universality properties related to thermodynamical observables? If we consider the chaotic billiards consisting of a single particle moving in a rigid environment of scatterers, then it does not make sense to talk about thermodynamics. Thus for systems considered in this work the answer is no. However, if one considers billiards of many particles, then thermodynamics (as a function of temperature) will influence the dynamics. We shall defer the study of such effects on universality to future work.
5) Is such universality related to spectral statistics of the corresponding quantum system, i.e., what is the relation between universality in classical chaotic systems and universality in chaotic quantum systems, as defined via the Bohigas-Giannoni-Schmit conjecture [7] ? This is a very interesting question, for which we do not have an answer. The finding that universality properties exist in both, classical and quantum chaos, may be a hint that such a relation actually exists. On the other hand, for universality in quantum chaos in the semi- classical regime, periodic orbits play a crucial role (via Gutzwillers trace formula). In contrast, in our study of chaotic classical billiards universality is captured in the length matrix of bouncing, zig-zag, non-periodic trajectories. In order to address such question further, we suggest to consider the path integral relation (in Euclidean, i.e. imaginary time)

which relates the quantum Hamltonian H to the classical Euclidean action
6. Transport Properties from Length of Trajectories
Above we have shown for the Bunimovich stadium billiard and for the Sinai billiard that they display universality properties via the statistical behaviour of the matrix of length of trajectories. Here we will show that such universal behaviour is related to relevant physical quantities. In particular we will extract transport properties from the length matrix (note the analogy to computation of transport properties in quantum chaos in semi-classical regime via Gutzwiller formula). As examples we consider the stadium billiard.
In systems for which the CLT is verified, the diffusive character is manifested by a linear relation between the time of travel and the variance of position. The diffusion coefficient d (in 2 dimensions) is given by the Einstein relation

where 


where travel time 


Based on this approach, we define a diffusion coefficient with respect to the variable

for the Bunmovich stadium billiard, which is a chaotic system with concave repeller/scatterer. We have chosen to analyze such system, and compute its transport properties because it reveals a very interesting non-standard diffusion behaviour. In a numerical modelling study of the stadium billiard, Borgognoni et al. [54] have studied its diffusion behaviour by testing if a linear relation holds between the time of travel and the variance of angular momentum. They found that a linear relation fits quite well their data and computed the diffusion coefficients as ratio of variance of angular momentum and time of travel (or number of bounces). However, in 2006, Bálint and Gouëzel [53] proved rigorously for the stadium billiard that a “non-standard” limit theorem holds, where the width does not follow the usual 

We carried out numerical simulations using trajectories of the length matrix 



We define the diffusion coefficient by

We have done statistical tests of 


we obtained for the linear fit 




Figure 8. Anomalous diffusion in stadium billiard. (a) Variance of 


Figure 8(a), compared to the fit with logarithmic correction giving 





7. Summary
This paper is about classical chaos occuring widely in nature, for example in astrophysics, meteorology and dynamics of the atmosphere, fluid and ocean dynamics, climate change, chemical reactions, biology, physiology, neuroscience, or medicine. We have suggested to extend random matrix theory, used in chaotic quantum systems, to classically chaotic and integrable systems. We have studied fully chaotic as well as integrable billiards and used a statistical description based on the length of trajectories to discriminate chaotic versus inte- grable behaviour.
Results:
1) In chaotic billiards (stadium and Sinai billiards), the NNS distribution 

2) The distribution of length matrix elements 

3) For the integrable rectangular billiard we find a correlation coefficient


4) In contrast, for integrable quantum systems the NNS distribution generally shows Poissonian behaviour with correlation coefficient 
Future directions:
1) We plan to do numerical studies to investigate if universality also holds in chaotic potential systems.
2) We hope that our findings may contribute to obtain a unified description of both, quantum and classical chaos, and help understanding why quantum chaos is typically weaker than classical chaos, e.g., via an effective quantum action [55] [56] .
3) The global statistical approach to classical chaos proposed here may help to give insight into the problem of ergodicity breaking in Hamiltonian systems (e.g., dense packing of discs in the Lorentz gas model [27] ).
Acknowledgements
We are thankful to Prof. L. J. Dubé for insightful discussions on chaotic dynamics and to O. Blondeau-Fournier for discussions and his assistance in performing simulations and analyses presented in Section 3.1 and 4.1. H. Kröger is grateful to Prof. Chernov for discussions on central limit theorems in chaotic billiards. This work has been supported by NSERC Canada.
Cite this paper
Jean-FrançoisLaprise,AhmadHosseinizadeh,HelmutKröger, (2015) Universality in Statistical Measures of Trajectories in Classical Billiard Systems. Applied Mathematics,06,1407-1425. doi: 10.4236/am.2015.68132
References
- 1. Mehta, M.L. (1960) On the Statistical Properties of Level Spacings in Nuclear Spectra. Nuclear Physics, 18, 395-419.
http://dx.doi.org/10.1016/0029-5582(60)90413-2 - 2. Dyson, F.J. (1962) Statistical Theory of the Energy Levels of Complex Systems, I. Journal of Mathematical Physics, 3, 140.
http://dx.doi.org/10.1063/1.1703773 - 3. Dyson, F.J. (1962) Statistical Theory of the Energy Levels of Complex Systems, II. Journal of Mathematical Physics, 3, 157.
http://dx.doi.org/10.1063/1.1703774 - 4. Dyson, F.J. (1962) Statistical Theory of the Energy Levels of Complex Systems, III. Journal of Mathematical Physics, 3, 166.
http://dx.doi.org/10.1063/1.1703775 - 5. Dyson, F.J. (1962) A Brownian Motion Model for the Eigenvalues of a Random Matrix. Journal of Mathematical Physics, 3, 1191.
http://dx.doi.org/10.1063/1.1703862 - 6. Mehta, M.L. (1991) Random Matrices and the Statistical Theory of Energy Levels. Academic Press, New York.
- 7. Bohigas, O., Giannoni, M.J. and Schmit, C. (1984) Characterization of Chaotic Quantum Spectra and Universality of Level Fluctuations Laws. Physical Review Letters, 52, 1.
http://dx.doi.org/10.1103/PhysRevLett.52.1 - 8. Bohigas, O. and Giannoni, M.J. (1983) Chaotic Motion and Random Matrix Theories. Lecture Notes in Physics, 209, 1-99.
http://dx.doi.org/10.1007/3-540-13392-5_1 - 9. Casati, G., Valz-Gris, F. and Guarnieri, I. (1980) On the Connection between Quantization of Nonintegrable Systems and Statistical Theory of Spectra. Lettere al Nuovo Cimento, 28, 279.
http://dx.doi.org/10.1007/BF02798790 - 10. Blümel, R. and Reinhardt, W.P. (1997) Chaos in Atomic Physics. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511524509 - 11. Stöckmann, H.J. (1999) Quantum Chaos. Cambridge University Press, Cambridge.
- 12. Guhr, T., Müller-Groeling, A. and Weidenmüller, H.A. (1998) Random-Matrix Theories in Quantum Physics: Common Concepts. Physics Reports, 299, 189-425.
http://dx.doi.org/10.1016/S0370-1573(97)00088-4 - 13. Haake, F. (2001) Quantum Signatures of Chaos. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-662-04506-0 - 14. Robnik, M. (1986) Antiunitary Symmetries and Energy Level Statistics. Lecture Notes in Physics, 263, 120-130.
http://dx.doi.org/10.1007/3-540-17171-1_9 - 15. Berry, M.V. (1985) Semiclassical Theory of Spectral Rigidity. Proceedings of the Royal Society of London A, 400, 229.
http://dx.doi.org/10.1098/rspa.1985.0078 - 16. Berry, M.V. (1987) The Bakerian Lecture: Quantum Chaology. Proceedings of the Royal Society of London A, 413, 183.
http://dx.doi.org/10.1098/rspa.1987.0109 - 17. Sieber, M. and Richter, K. (2001) Correlations between Periodic Orbits and Their Rôle in Spectral Statistics. Physica Scripta, T90, 128.
http://dx.doi.org/10.1238/Physica.Topical.090a00128 - 18. Müller, S., Heusler, S., Braun, P., Haake, F. and Altland, A. (2005) Periodic-Orbit Theory of Universality in Quantum Chaos. Physical Review E, 72, Article ID: 046207.
http://dx.doi.org/10.1103/PhysRevE.72.046207 - 19. Müller, S., Heusler, S., Braun, P., Haake, F. and Altland, A. (2004) Semiclassical Foundation of Universality in Quantum Chaos. Physical Review Letters, 93, Article ID: 014103.
http://dx.doi.org/10.1103/PhysRevLett.93.014103 - 20. Keating, J.P. and Müller, S. (2007) Resummation and the Semiclassical Theory of Spectral Statistics. Proceedings of the Royal Society of London A, 463, 3241-3250.
http://dx.doi.org/10.1098/rspa.2007.0178 - 21. Bunimovich, L.A. and Sinai, Y.G. (1981) Statistical Properties of Lorentz Gas with Periodic Configuration of Scatterers. Communications in Mathematical Physics, 78, 479-497.
http://dx.doi.org/10.1007/BF02046760 - 22. Burton, R. and Denker, M. (1987) On the Central Limit Theorem for Dynamical Systems. Transactions of the American Mathematical Society, 302, 715.
http://dx.doi.org/10.1090/S0002-9947-1987-0891642-6 - 23. Bunimovich, L.A., Sinai, Y.G. and Chernov, N.I. (1991) Statistical Properties of Two-Dimensional Hyperbolic Billiards. Russian Mathematical Surveys, 46, 47-106.
http://dx.doi.org/10.1070/RM1991v046n04ABEH002827 - 24. Chernov, N.I. (1994) Statistical Properties of the Periodic Lorentz Gas. Multidimensional Case. Journal of Statistical Physics, 74, 11-53.
http://dx.doi.org/10.1007/BF02186805 - 25. Liverani, C. (1995) Ergodicity in Hamiltonian Systems. Proceedings of the International Congress on Dynamical Systems, Montevideo, 56.
http://dx.doi.org/10.1007/978-3-642-61215-2_3 - 26. Chernov, N.I. (1995) Limit Theorems and Markov Approximations for Chaotic Dynamical Systems. Probability Theory and Related Fields, 101, 321-362.
http://dx.doi.org/10.1007/BF01200500 - 27. Gaspard, P. (1998) Chaos, Scattering and Statistical Mechanics. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511628856 - 28. Argaman, N., Dittes, F.M., Doron, E., Keating, J.P., Kitaev, A.Y., Sieber, M. and Smilansky, U. (1993) Correlations in the Actions of Periodic Orbits Derived from Quantum Chaos. Physical Review Letters, 71, 4326-4329.
http://dx.doi.org/10.1103/PhysRevLett.71.4326 - 29. Dittes, F.M., Doron, E. and Smilansky, U. (1994) Long-Time Behaviour of the Semiclassical Baker’s Map. Physical Review E, 49, R963-R966.
http://dx.doi.org/10.1103/PhysRevE.49.R963 - 30. Aurich, R. and Sieber, M. (1994] An Exponentially Increasing Semiclassical Spectral Form Factor for a Class of Chaotic Systems. Journal of Physics A: Mathematical and General, 27, 1967-1979.
http://dx.doi.org/10.1088/0305-4470/27/6/021 - 31. Cohen, D., Primack, H. and Smilansky, U. (1998) Quantal—Classical Duality and the Semiclassical Trace Formula. Annals of Physics, 264, 108-170.
http://dx.doi.org/10.1006/aphy.1997.5776 - 32. Tanner, G. (1999) Periodic Orbit Action Correlations in the Baker Map. Journal of Physics A: Mathematical and General, 32, 5071-5085.
http://dx.doi.org/10.1088/0305-4470/32/27/307 - 33. Sano, M.M. (2000) Statistical Properties of Actions of Periodic Orbits. Chaos, 10, 195.
http://dx.doi.org/10.1063/1.166485 - 34. Primack, H. and Smilansky, U. (2000) The Quantum Three-Dimensional Sinai Billiard—A Semiclassical Analysis. Physics Reports, 327, 1-107.
http://dx.doi.org/10.1016/S0370-1573(99)00093-9 - 35. Smilansky, U. and Verdene, B. (2003) Action Correlations and Random Matrix Theory. Journal of Physics A: Mathematical and General, 36, 3525-3549.
http://dx.doi.org/10.1088/0305-4470/36/12/338 - 36. Laprise, J.F., Blondeau-Fournier, O., Kröger, J., Kröger, H., St.-Louis, P.Y., Dubé, L.J., Endress, E., Burra, A., Zomorrodi, R., Melkonyan, G. and Moriarty, K.J.M. (2008) Universality of Level Spacing Distributions in Classical Chaos. Physics Letters A, 372, 4574-4577.
http://dx.doi.org/10.1016/j.physleta.2008.04.044 - 37. Laprise, J.F., Hosseinizadeh, A., Lamy-Poirier, J., Zomorrodi, R., Kröger, J. and Kröger, H., (2010) Universality in Level Spacing Fluctuations of a Chaotic Optical Billiard. Physics Letters A, 374, 2000-2004.
http://dx.doi.org/10.1016/j.physleta.2010.02.057 - 38. Alekseev, V.M. and Yakobson, M.V. (1981) Symbolic Dynamics and Hyperbolic Dynamic Systems. Physics Reports, 75, 290-325.
http://dx.doi.org/10.1016/0370-1573(81)90186-1 - 39. Berry, M.V. and Tabor, M. (1977) Level Clustering in the Regular Spectrum. Proceedings of the Royal Society of London A, 356, 375-394.
http://dx.doi.org/10.1098/rspa.1977.0140 - 40. Casati, G., Chirikov, B.V. and Guarneri, I. (1985) Energy-Level Statistics of Integrable Quantum Systems. Physical Review Letters, 54, 1350-1353.
http://dx.doi.org/10.1103/PhysRevLett.54.1350 - 41. Seligman, T.H. and Verbaarschot, J.J.M. (1986) Energy-Level Statistics of Integrable Quantum Systems. Physical Review Letters, 56, 2767.
http://dx.doi.org/10.1103/PhysRevLett.56.2767 - 42. Chakrabarti, B. and Hu, B. (2003) Level Correlation in Coupled Harmonic Oscillator Systems. Physics Letters A, 315, 93-100.
http://dx.doi.org/10.1016/S0375-9601(03)01001-6 - 43. Chernov, N. (1997) Entropy, Lyapunov Exponents, and Mean Free Path for Billiards. Journal of Statistical Physics, 88, 1-29.
http://dx.doi.org/10.1007/BF02508462 - 44. Sinai, Y.G. (1963) On the Foundations of the Ergodic Hypothesis for a Dynamical System of Statistical Mechanics. Soviet Mathematics Doklady, 4, 1818.
- 45. Bruus, H. and d’Auriac, J.C.A. (1997) Energy Level Statistics of the Two-Dimensional Hubbard Model at Low Filling. Physical Review B, 55, 9142-9159.
http://dx.doi.org/10.1103/PhysRevB.55.9142 - 46. Seligman, T.H., Verbaarschot, J.J.M. and Zirnbauer, M.R. (1984) Quantum Spectra and Transition from Regular to Chaotic Classical Motion. Physical Review Letters, 53, 215-217.
http://dx.doi.org/10.1103/PhysRevLett.53.215 - 47. Brody, T.A., Flores, J., French, J.B., Mello, P.A., Pandey, A. and Wong, S.S.M. (1981) Random-Matrix Physics: Spectrum and Strength Fluctuations. Reviews of Modern Physics, 53, 385-479.
http://dx.doi.org/10.1103/RevModPhys.53.385 - 48. Bunimovich, L.A. (1974) On Ergodic Properties of Certain Billiards. Functional Analysis and Its Applications, 8, 73-74.
- 49. Bunimovich, L.A. (1979) On the Ergodic Properties of Nowhere Dispersing Billiards. Communications in Mathematical Physics, 65, 295-312.
http://dx.doi.org/10.1007/BF01197884 - 50. Bohigas, O., Haq, R.U. and Pandey, A. (1983) Fluctuation Properties of Nuclear Energy Levels and Widths: Comparison of Theory with Experiment. In: Böckhoff, K.H., Ed., Nuclear Data for Science and Technology, Reidel, Dordrecht, 809-813.
- 51. Szász, D. and Varjú, T. (2007) Limit Laws and Recurrence for the Planar Lorentz Process with Infinite Horizon. Journal of Statistical Physics, 129, 59-80.
http://dx.doi.org/10.1007/s10955-007-9367-0 - 52. Chernov, N. and Markarian, R. (2006) Chaotic Billiards. Mathematical Surveys and Monographs, American Mathematical Society, Providence, Vol. 127, 7.2.
- 53. Bálint, P. and Gouëzel, S. (2006) Limit Theorems in the Stadium Billiard. Communications in Mathematical Physics, 263, 461-512.
http://dx.doi.org/10.1007/s00220-005-1511-6 - 54. Borgonovi, F., Casati, G. and Li, B. (1996) Diffusion and Localization in Chaotic Billiards. Physical Review Letters, 77, 4744-4747.
http://dx.doi.org/10.1103/PhysRevLett.77.4744 - 55. Jirari, H., Kröger, H., Luo, X.Q., Moriarty, K.J.M. and Rubin, S.G. (2001) Closed Path Integrals and the Quantum Action. Physical Review Letters, 86, 187-191.
http://dx.doi.org/10.1103/PhysRevLett.86.187 - 56. Caron, L.A., Jirari, H., Kröger, H., Luo, X.Q., Melkonyan, G. and Moriarty, K.J.M. (2001) Quantum Chaos at Finite Temperature. Physics Letters A, 288, 145-153.
http://dx.doi.org/10.1016/S0375-9601(01)00555-2






