Applied Mathematics
Vol.5 No.13(2014), Article ID:47987,11 pages
DOI:10.4236/am.2014.513202
An Error Controlled Method to Determine the Stellar Density Function in a Region of the Sky
Mohammed Adel Sharaf1, Zainab Ahmed Mominkhan2
1Department of Astronomy, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia
2Department of Mathematics, College of Science for Girls King Abdulaziz University, Jeddah, Saudi Arabia
Email: Sharaf_adel@hotmail.com, Zammomin @hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 18 April 2014; revised 24 May 2014; accepted 9 June 2014
ABSTRACT
In this paper, a reliable computational tool will be developed for the determination of the parameters of the stellar density function in a region of the sky with complete error controlled estimates. Of these error estimates are, the variance of the fit, the variance of the least squares solutions vector, the average square distance between the exact and the least-squares solutions, finally the variance of the density stellar function due to the variance of the least squares solutions vector. Moreover, all these estimates are given in closed analytical forms.
Keywords:Astrostatistics, Stellar Density Function, Computational Astrophysics

1. Introduction
Modern observational astronomy has been characterized by an enormous growth of data stimulated by the advent of new technologies in telescopes, detectors and computations. The new astronomical data give rise to innumerable statistical problems [1] . Moreover, empirical astrophysics researches have seen a paradigm shift in recent years in that it routinely involves data mining of large multi wavelength data sets, requiring complex automated processes that must invoke a very diverse set of statistical techniques (e.g. [2] [3] ).
On the other hand, one of the most crucial pieces of information needed in astronomy is the stellar density function in a region of the sky, due to the wealth of information on galactic structure gained directly from a study of the variations in the stellar density (e.g. [4] -[6] ).
Although the least-squares method is the most powerful technique that has been devised
for the problems of astrostatistics in general [7]
, it is at the same time exceedingly critical. This is because the least-squares
method suffers from the deficiency that, its estimation procedure does not have
detecting and controlling techniques for the sensitivity of the solution to the
optimization criterion of the variance
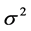 is minimum. As a result, there may exist a situation in which there are many significantly
different solutions that reduce the variance
is minimum. As a result, there may exist a situation in which there are many significantly
different solutions that reduce the variance
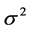 to an acceptable small value.
to an acceptable small value.
At this stage we should point out that 1) the accuracy of the estimators and the
accuracy of the fitted curve are two distinct problems; and 2) an accurate estimator
will always produce small variance, but small variance does not guarantee an accurate
estimator. This could be seen from Equation (2) by noting that the lower bounds
for the average square distance between the exact and the least-squares values is
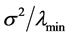 which may be large even if
which may be large even if
 is very small, depending on the magnitude of the minimum eigenvalue,
is very small, depending on the magnitude of the minimum eigenvalue,
 , of the coefficient matrix of the least-squares normal
equations. Unless detecting and controlling this situation, it is not possible to
make a well-defined decision about the results obtained from the applications of
the least squares method.
, of the coefficient matrix of the least-squares normal
equations. Unless detecting and controlling this situation, it is not possible to
make a well-defined decision about the results obtained from the applications of
the least squares method.
The importance of the stellar density function as mentioned very briefly as in the above and the existing practical difficulties due to the deficiency of the error estimation and controlling had motivated our work: to develop a reliable computational tool for the determination of the parameters of the stellar density with complete error estimates. Of these error estimates are, the variance of the fit, the variance of the least squares solutions vector, the average square distance between the exact and the least-squares solutions, finally the variance of the density stellar function due to the variance of the least squares solutions vector.
By this we aim at giving an idea on what may called an “accepted solution set” for the parameters of the stellar density functions and the associated variances by the selected tolerances for the error estimates.
Before starting the analysis, it is profitable, to give brief notes on the structure of the paper as follows.
1-Using Fourier transform to obtain analytical solution of the density function;
2-Using the least squares method to find second order polynomial for each of the apparent and absolute magnitudes distributions;
3-Using steps 1 & 2, we established analytical expressions of the density function with coefficients directly obtained from observations.
2. Linear Least Squares Fit
Let
![]() be represented by the general linear expression of the form:
be represented by the general linear expression of the form:
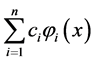 where
where
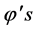 are linear independent functions of
are linear independent functions of . Let
. Let
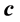 be the vector of the exact values of the
be the vector of the exact values of the
 coefficients and
coefficients and
 the least squares estimators of
the least squares estimators of
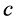 obtained from the solution of the normal equations of the form
obtained from the solution of the normal equations of the form . The coefficients matrix
. The coefficients matrix
 is symmetric positive definite, that is, all its eigenvalues
is symmetric positive definite, that is, all its eigenvalues
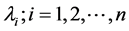 are positive. Let E(z) denotes the expectation of z and
are positive. Let E(z) denotes the expectation of z and
 the variance of the fit, defined as:
the variance of the fit, defined as:
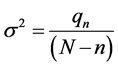
where
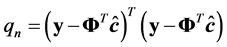
![]() is the number of observations,
is the number of observations,
![]() is the vector with elements
is the vector with elements
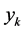 and
and
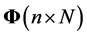 has elements
has elements . The transpose of a vector or a matrix
is indicated by the superscript “
. The transpose of a vector or a matrix
is indicated by the superscript “![]() ”.
”.
According to the least squares criterion, it could be shown that [8]
1-The estimators
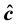 obtained by the least squares method gives the minimum of
obtained by the least squares method gives the minimum of![]() .
.
2-The estimators
 of the coefficients
of the coefficients , obtained by the least squares method,
are unbiased; i.e.
, obtained by the least squares method,
are unbiased; i.e.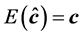 .
.
3-The variance-covariance matrix
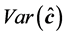 of the unbiased estimators
of the unbiased estimators
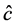 is given by:
is given by:
 (1)
(1)
where
 is the inverse of the matrix
is the inverse of the matrix![]() .
.
4-The average squared distance between
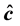 and
and
 is:
is:
 . (2)
. (2)
Also it should be noted that, if the precision is measured by probable error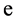 , then:
, then:
![]() .
.
Finally, if
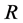 is a linear function of the independent variables
is a linear function of the independent variables
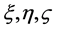 given by
given by
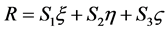 , (3.1)
, (3.1)
then [9]
 , (3.2)
, (3.2)
where
![]() is the variance of
is the variance of
 and
and
 are the variances of the independent variables
are the variances of the independent variables
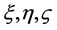
3. Basic Equations
3.1. The Integral Equation of the Problem
The absolute magnitude, M of a star is given in terms of the apparent magnitude
![]() and parallax
and parallax
![]() (in second of arc) by
(in second of arc) by
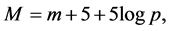
where M is thus defined in terms of the standard distance of 10 parsecs. We write, for convenience,
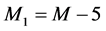 so that
so that
 is defined in terms of the standard distance of 1 parsec, and
is defined in terms of the standard distance of 1 parsec, and
 .
.
In the above formulae the base of the logarithm is 10.
We shall refer to
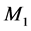 in this connection as the modified absolute magnitude. Also, with r measured in
parsecs, we have
in this connection as the modified absolute magnitude. Also, with r measured in
parsecs, we have
 and
and
 .
.
Let
 be the frequency function of
be the frequency function of
 and
and
 denote the total number of stars with apparent magnitude between
denote the total number of stars with apparent magnitude between
![]() and
and
 in small region of the sky subtends a solid angle
in small region of the sky subtends a solid angle
![]() in the distance interval
in the distance interval
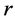 and
and
 where the density function is
where the density function is , then (Trumple & Weaver1953)
, then (Trumple & Weaver1953)
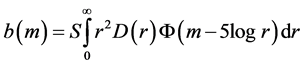 .
.
Let
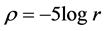 then
then

Let

then
![]() .
.
Consequently
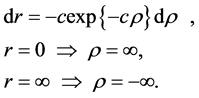
Hence
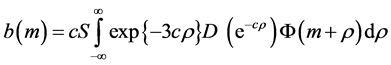 or
or
 (4)
(4)
where
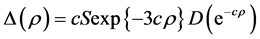 , (5)
, (5)
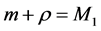 . (6)
. (6)
Equation (4) is the basic integral equation to be solved for the density function
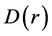 as will be shown latter.
as will be shown latter.
3.2. Maxwellian Distributions of the Magnitudes
Let the distributions of the apparent and absolute magnitudes are Maxwellian in form. We assume that
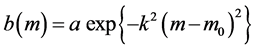 , (7.1)
, (7.1)
 , (7.2)
, (7.2)
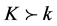 . (7.3)
. (7.3)
As regards Equation (7.1), this is the form found to satisfy the star counts for
a given galactic latitude in the exhaustive investigation by many authors. The parameters ,
,
 and
and
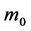 are to be regarded as functions of galactic latitude and possibly also of galactic
longitude.
are to be regarded as functions of galactic latitude and possibly also of galactic
longitude.
Equation (7.2) must be regard as applicable only to a particular spectral type or
subdivision of spectral type. In many studies of the distribution of absolute magnitudes,
the separation of stars into the giant and dwarf classes is recognized, that in
dealing with a given spectral type we represent the function
 as the sum of two Maxwellian expressions of the type (7.2). In the following analysis,
we deal with a single Maxwellian function only.
as the sum of two Maxwellian expressions of the type (7.2). In the following analysis,
we deal with a single Maxwellian function only.
The condition (7.3) implies that the dispersion about the mean is less for absolute magnitudes of a given spectral type than for the apparent magnitudes. This is in accordance with observations, for the giants or for the dwarfs.
4. The Normal Equations and the Associated Error Analysis
Taking the natural logarithm of Equations (7.1) and (7.2) we get,
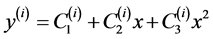 , (8)
, (8)
where
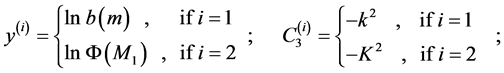 (9)
(9)
 (10)
(10)
and
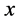 stands for
stands for
![]() if
if
![]() and for
and for
![]() if
if
![]()
Since,
 are known from observations for all
are known from observations for all , then according to Section2,the normal
equations associated with Equations (8) are:
, then according to Section2,the normal
equations associated with Equations (8) are:
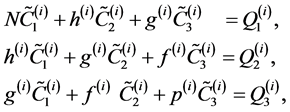 (11)
(11)
where
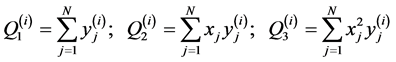 (12)
(12)
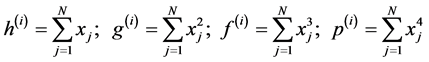 (13)
(13)
In the following two sections, the solutions of the normal equations for
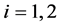 together with the associated error analysis will be developed in closed analytical
forms.
together with the associated error analysis will be developed in closed analytical
forms.
4.1. Solutions of the Normal Equations
The solutions of the normal Equations (11) for
 are given exactly as,
are given exactly as,
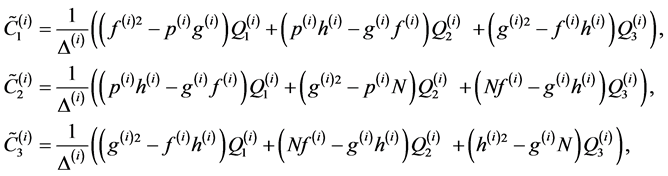 (14)
(14)
where
 . (15)
. (15)
4.2. Error Analysis
According to Section 2, we deduce for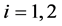 , that:
, that:
1-The variance of the fit is:
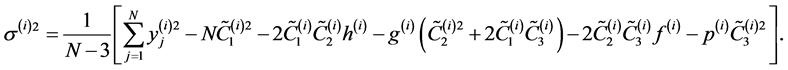 (16)
(16)
2-The variance of the solutions are:
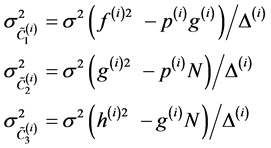 , (17)
, (17)
3-The average squared distance between the least square solutions and the exact solutions is
 . (18)
. (18)
5. Analytical Expression of the Density Function D(r)
Recalling the Fourier transform
![]() of the function
of the function
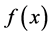 as:
as:
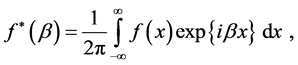 (19.1)
(19.1)
while its inverse is
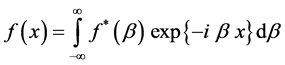 . (19.2)
. (19.2)
Multiply Equation (4) by
 and integrate between
and integrate between , then
, then
 , (20)
, (20)
where
 .
.
Let
 then,
then,
 also
also
 ,
,
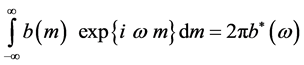 .
.
Then Equation (20) reduces to
 also
also
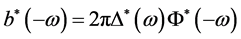 .
.
The inverse of Fourier transform of
 is:
is:

then
 , (21)
, (21)
where
![]() and
and
![]() are the Fourier integrals of
are the Fourier integrals of
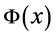 and
and
 respectively where
respectively where
 ;
;
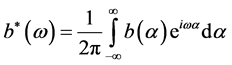
![]() could written as
could written as
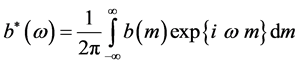 . (22)
. (22)
Using Equation (7.1) in Equation (22) the later becomes:
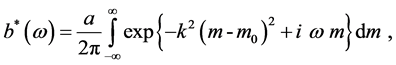
or, on setting ,we get:
,we get:
 evaluating the integral on the right hand side we get
evaluating the integral on the right hand side we get
 (23)
(23)
Similarly, as in deriving Equation (23) we can get for
![]() the expression:
the expression:
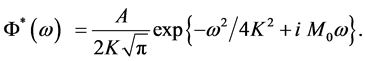 (24)
(24)
Now, substituting Equations (23) and (24) into Equation (21) we get,
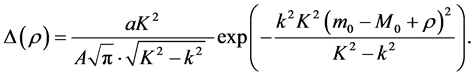
Using Equation (6) and remembering that
 we obtain for the density function the expression:
we obtain for the density function the expression:
 . (25)
. (25)
6. Empirical Determination of the Density Function D(r) and Its Accepted Solution Set
In what follows empirical expression of the density function
 and its variance will be established in literal closed forms.
and its variance will be established in literal closed forms.
6.1. Empirical Expression
Substituting Equations (9) and (10) into Equation (25), we get for the density function
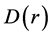 the empirical expression
the empirical expression
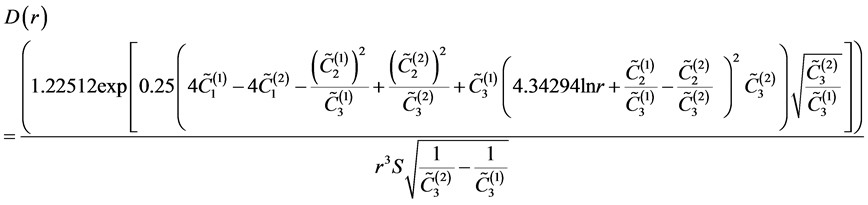 (26)
(26)
where
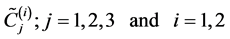 are the solutions of the normal equations (Equations (14))
are the solutions of the normal equations (Equations (14))
6.2. The Variance
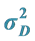
Since
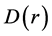 function of
function of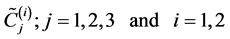 , then what is the variance
, then what is the variance
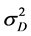 due to the variances
due to the variances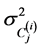 ? The following analysis is devoted for
the answer of this question.
? The following analysis is devoted for
the answer of this question.
Define
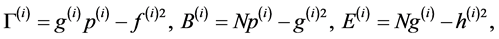 (27.1)
(27.1)
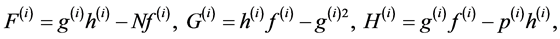 (27.2)
(27.2)
 , (28.1)
, (28.1)
 , (28.2)
, (28.2)
 , (28.3)
, (28.3)
therefore we have
 , (29.1)
, (29.1)
 , (29.2)
, (29.2)
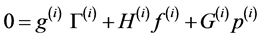 , (29.3)
, (29.3)
 , (30.1)
, (30.1)
 , (30.2)
, (30.2)
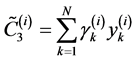 . (30.3)
. (30.3)
From Equations (29) we get
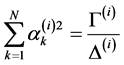 , (31.1)
, (31.1)
 , (31.2)
, (31.2)
 . (31.3)
. (31.3)
Multiply Equations (28.1) and (28.2) and then summing, we get
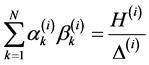 , (32.1)
, (32.1)
similarly
 , (32.2)
, (32.2)
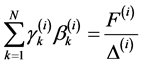 . (32.3)
. (32.3)
Since
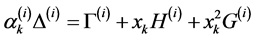 , (33)
, (33)
then summing we have
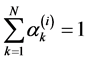 , (34.1)
, (34.1)
similarly
 (34.2)
(34.2)
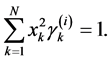 . (34.3)
. (34.3)
Multiply Equation (33) by
![]() and summing we get
and summing we get
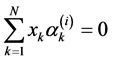 , (35.1)
, (35.1)
similarly
 , (35.1)
, (35.1)
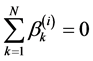 , (35.2)
, (35.2)
 , (35.3)
, (35.3)
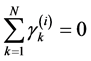 , (35.4)
, (35.4)
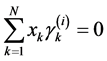 . (35.5)
. (35.5)
Since
![]() are the least squares solutions, then the corresponding residual,
are the least squares solutions, then the corresponding residual,
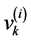 is given by:
is given by:
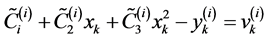 , (36)
, (36)
consequently,
 . (37)
. (37)
According to Section 2, we have
 . (38)
. (38)
where
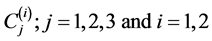 are the exact values of the unknowns and
are the exact values of the unknowns and
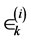 is the error associated with
is the error associated with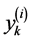 .
.
Multiply Equations (38) and (37) by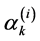 , subtracting, then summing we get
, subtracting, then summing we get
 , (39.1)
, (39.1)
similarly
 , (39.2)
, (39.2)
 , (39.3)
, (39.3)
let us take the error,
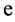 , of the density function
, of the density function
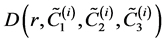 in the sense
in the sense

then assuming that the errors
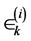 in Equations (39) are small, then we can write
in Equations (39) are small, then we can write
 with sufficient accuracy by means of Taylor expansion as:
with sufficient accuracy by means of Taylor expansion as:

where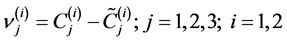 ,then using Equations(39) we get
,then using Equations(39) we get
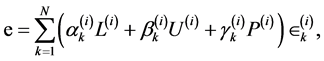 (40)
(40)
where
 .
.
Now, in Equation (40), e is linear function of the errors ; hence, then according to Equation (3)
we have
; hence, then according to Equation (3)
we have
 .
.
Using Equations (31), (32) and (17) we finally get
 , (41)
, (41)
where
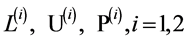 are given as
are given as
 , (42.1)
, (42.1)
 , (42.1)
, (42.1)
 (42.3)
(42.3)
 , (42.4)
, (42.4)
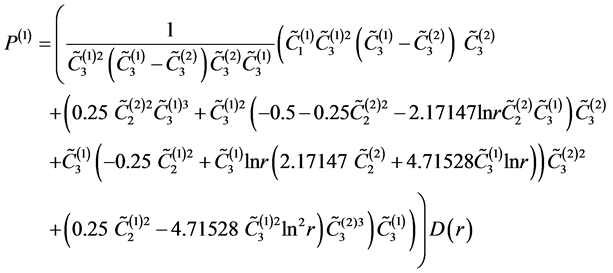 (42.5)
(42.5)
 (42.6)
(42.6)
6.3. The Variances of k2, K2, m0, M0, a, A
Since each of the constants
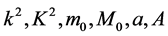 is a function of the least squares solutions, the by the same arguments as for Equations
(42) we get
is a function of the least squares solutions, the by the same arguments as for Equations
(42) we get
 (17)
(17)
 (43.1)
(43.1)
 (43.2)
(43.2)
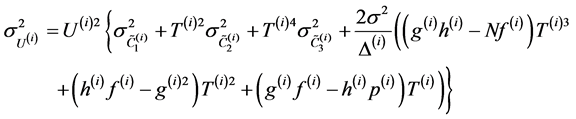 (43.3)
(43.3)
where
 (44)
(44)
6.4. An Accepted Solution Set for D(r)
Due to the above mentioned practical difficulties encountered in most applications
of the least squares method we should at this stage reformalize the concept of an
“acceptably small” variance. We may define an acceptable solution set to the determination
of
 as:
as:
 (45)
(45)
where Tol and
![]() small numbers. In writing Equation (45) we do not mean to establish this particular
definition of an acceptable solution set, as it is only intended to give the users
of the least squares method for
small numbers. In writing Equation (45) we do not mean to establish this particular
definition of an acceptable solution set, as it is only intended to give the users
of the least squares method for
 some degree of concreteness to the general idea of an acceptable solution set.
some degree of concreteness to the general idea of an acceptable solution set.
5. Conclusion
In conclusion, a reliable computational tool was developed in the present paper for the determination of the parameters of the stellar density function in a region of the sky with complete error controlled estimates. Of these error estimates are, the variance of the fit, the variance of the least squares solutions vector, the average square distance between the exact and the least-squares solutions, finally the variance of the density stellar function due to the variance of the least squares solutions vector. Moreover, all these estimates are given in closed analytical forms.
References
- Feigelson, E.D and Babu, J.B (2012) Modern Statistical Methods for Astronomy with Applications. Cambridge University Press, Cambridge.
- Sharaf, M.A, Issa, I.A. and Saad, A.S. (2003) Method for the Determination of Cosmic Distances. New Astronomy, 8, 15-21. http://dx.doi.org/10.1016/S1384-1076(02)00198-7
- Sharaf, M.A. and Sendi A.M. (2010) Computational Developments for Distance Determination of Stellar Groups. Journal of Astrophysics and Astronomy, 31, 3-16. http://dx.doi.org/10.1007/s12036-010-0002-0
- Trumpler, R.J. and Weaver, H.F. (1953) Statistical Astronomy. Dover Publication, Inc., New York.
- Robinson, R.M. (1985) The Cosmological Distance Ladder. W.H. Freeman and Company, New York.
- Binney, J. and Merrifield, M. (1998) Galactic Astronomy. Princeton University Press, Princeton.
- Andreon, S. and Hurn, M. (2013) Measurement Errors and Scaling Relations in Astrophysics: A Review. Statistical Analysis and Data Mining: The ASA Data Science Journal, 6, 15-33.
- Kopal, Z. and Sharaf, M.A. (1980) Linear Analysis of the Light Curves of Eclipsing Variables. Astrophysics and Space Science, 70, 77-101. http://dx.doi.org/10.1007/BF00641665
- Bevington, P.R and Robinson, D.K. (1992) Data Reduction and Error Analysis for the Physical Sciences. McGraw-Hill, New York.

