Applied Mathematics
Vol.3 No.10A(2012), Article ID:24133,5 pages DOI:10.4236/am.2012.330201
Optimization of Quantizer’s Segment Treshold Using Spline Approximations for Optimal Compressor Function
1Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade, Serbia
2Department of Telecommunications, Faculty of Electronic Engineering, University of Niš, Niš, Serbia
3Mathematical Department, Faculty of Occupational Safety, University of Niš, Niš, Serbia
Email: *velimirovic.lazar@gmail.com, zoran.peric@elfak.ni.ac.rs
Received July 9, 2012; revised August 9, 2012; accepted August 16, 2012
Keywords: Optimization of Quantizer’s Segment Threshold; Mean Square Error; Second-Degree Spline Functions; Compressor Function
ABSTRACT
In this paper, the optimization of quantizer’s segment threshold is done. The quantizer is designed on the basis of approximative spline functions. Coefficients on which we form approximative spline functions are calculated by minimization mean square error (MSE). For coefficients determined in this way, spline functions by which optimal compressor function is approximated are obtained. For the quantizer designed on the basis of approximative spline functions, segment threshold is numerically determined depending on maximal value of the signal to quantization noise ratio (SQNR). Thus, quantizer with optimized segment threshold is achieved. It is shown that by quantizer model designed in this way and proposed in this paper, the SQNR that is very close to SQNR of nonlinear optimal companding quantizer is achieved.
1. Introduction
Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set—such as rounding values to some unit of precision. The most common type of quantization is known as scalar quantization. A device or algorithmic function that performs quantization is called a quantizer [1-3].
Quantizers can be uniform and nonuniform. Uniform quantizers are suitable for signals that have approximately uniform distribution. How most of the signals do not have a uniform distribution there is a need for using nonuniform quantizer [1-3]. One of the most used methods for the realization of the nonuniform quantizer is companding technique, in which a specific compressor function is applied on an input signal. The most often used compressor functions are optimal compressor function [1-3]. The optimal compressor function gives the maximum signal to quantization noise ratio (SQNR) for the reference variance of the input signal. By knowing compressor function, model quantizer is completely defined. However, although easy for analysis, it is shown that this model is very difficult to realize [1-3]. Therefore, in order to achieve easier practical realization, approximation of the optimal compressor function and linearization of the optimal compressor function is performed.
A comprehensive analysis of SQNR behavior in a wide range of variances for the piecewise uniform scalar quantizer PUSQ designed for a Laplacian source according to the piecewise linear approximation to the optimal compressor law is reported in [4]. The linearization of the optimal compressor function is done in [5]. The demerit of method described by [5] is a high complexity of quantizer and high complexity of coding and decoding. The analysis of compressor function for Laplacian source is shown in [6]. Quantizer designed on the basis of approximative spline functions, whose support region is divided on segments of equal size is described in [7].
In this paper, in order to reduce complexity and maintenance of a reasonably good performance of quantizer, we develop a new method of construction quantizer which introduces optimization of the segment threshold and different number of cells per segments. The number of cells per segments is determined depending on value of optimized segment threshold. Also, depending on value of optimized segment threshold, approximate spline functions, by which the optimal compressor function is approximated, are determined. Unlike with the quantizer described in [7], the support region of proposed quantizer model is not divided on segments of equal size. Segments’size at the proposed model depends on segment threshold that is being optimized. The value of segment threshold depends on the size of the support region. In papers [8-10] detailed analyses are performed on which the importance of support region choice could be well seen. In the papers mentioned above, the influence of support region choice on scalar quantizer performances that are designed for Laplacian source is analysed. By designing the proposed quantizer based on approximate spline functions and optimized threshold segment, SQNR that is close to that of the nonlinear optimal companding quantizer is obtained.
The rest of the paper is organized as follows: In Section 2 the detailed description of spline functions of the second-degree and optimal compressor function is given. Design of quantizer based on spline functions of the second-degree is described in Section 3. The procedure for optimization of the segment threshold is described in Section 4. Finally, Section 5 presents numerical results and discusses their implications.
2. Approximate Second-Degree Spline Functions and Optimal Compressor Function
The theory of approximation is the area of numerical mathematics that deals with problems of replacing one function with other. It is shown that the spline of degree 2 better approximates the optimal compressor function than the spline of degree 1 [7]. Therefore, in this paper, the approximation of the optimal compressor function using spline function of the second-degree is done.
A function Q is called a spline of degree 2 if [11]:
1) The domain of Q is an interval [a, b].
2) Q and Q’ are continuous on [a, b].
3) There are points xi (called knots) such that a = x0 < x1 < ··· < xL = b and Q is a polynomial of degree at most 2 on each subinterval [xi, xi+1].
In brief, a quadratic spline is a continuously differenttiable piecewise quadratic function, where quadratic includes all linear combinations of the basic functions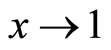 , x, x2. The second-degree spline, also called a quadratic spline, is consisted of parabola parts between two consecutive knotes, but elected to have the same tangent at knote [11]. The approximate quadratic spline function g(x), which approximates a nonlinear compressed function c(x), has the following form [11]:
, x, x2. The second-degree spline, also called a quadratic spline, is consisted of parabola parts between two consecutive knotes, but elected to have the same tangent at knote [11]. The approximate quadratic spline function g(x), which approximates a nonlinear compressed function c(x), has the following form [11]:
 (1)
(1)
In this paper, the coefficients of the second-degree spline, ri, pi and qi, i = 1, ···, L, are determined by minimizing the mean-square error (MSE) as follows:
 (2)
(2)
 (3)
(3)
The optimal compressor function c(x) by which the maximum SQNR is achieved for the reference variance of an input signal is defined as [1-3]:
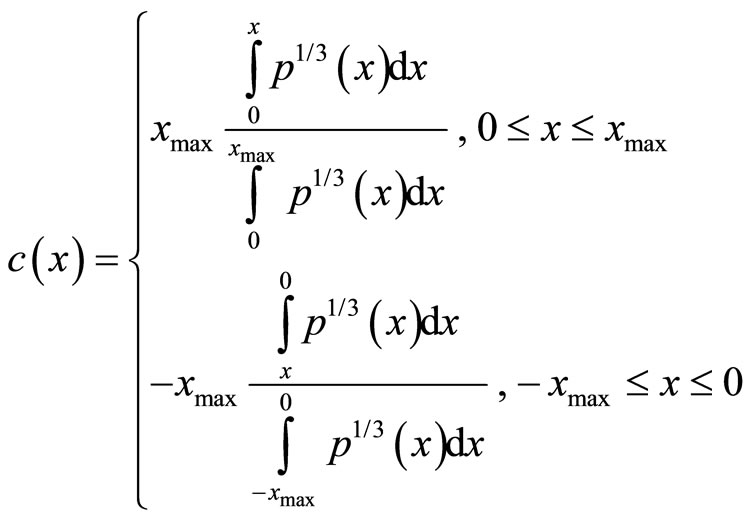 (4)
(4)
Without diminishing the generality, the quantizer design will be done for the reference input variance of 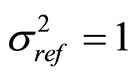 and
and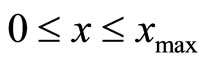 .
.
3. Design of Quantizer Based on Approximate Second-Degree Spline Functions
The performances of a quantizer are usually specified in terms of SQNR [1-3]:
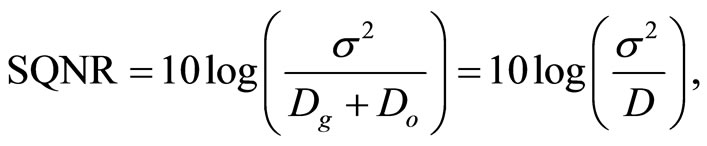 (5)
(5)
measured in decibels [dB], with 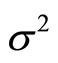 denoting the variance of an input signal x and with D denoting the total distortion. The total distortion D is equal to the sum of the granular distortion Dg and the overload distortion Do. The overload distortion Do is determined as follows [1-3]:
denoting the variance of an input signal x and with D denoting the total distortion. The total distortion D is equal to the sum of the granular distortion Dg and the overload distortion Do. The overload distortion Do is determined as follows [1-3]:
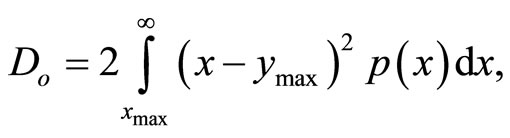 (6)
(6)
where p(x) is Laplacian probability density function (PDF) which is defined as follows [1]:
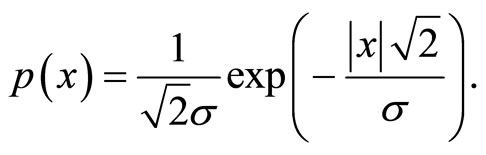 (7)
(7)
In the rest of the paper we assume symmetry about zero in the proposed quantizer model design. The Laplacian PDF is symmetrical about zero. Namely, without loss of generality, we assume that information source is Laplacian source with memoryless property, the unit variance and zero mean value. The reproduction level ymax is determined from the condition:
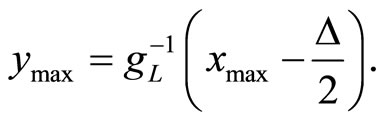 (8)
(8)
The gL presents the approximate spline function of the last segment (see Figure 1). The step size is equal to:
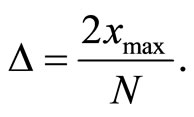 (9)
(9)
The optimal support region value of the proposed quantizer is as follows [5]:
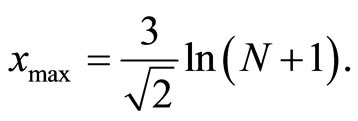 (10)
(10)
The total number of the reproduction levels per segments in the first quadrant is:
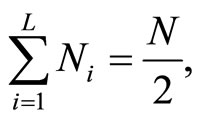 (11)
(11)
where the optimal number of reproduction levels per segments, Ni, is determined from the following condition:
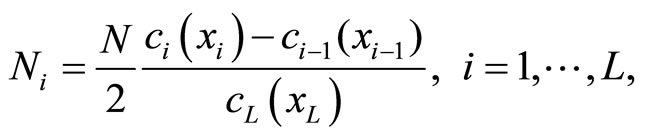 (12)
(12)
Reproduction levels are determined as the solution of the approximate spline function as follows:
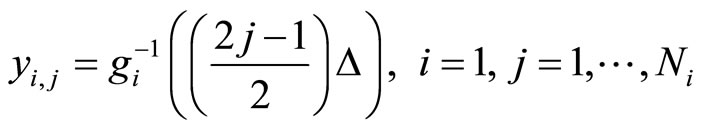 (13)
(13)
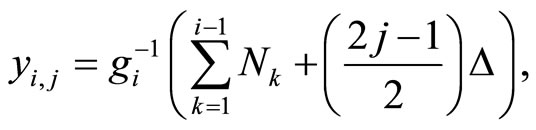 (14)
(14)
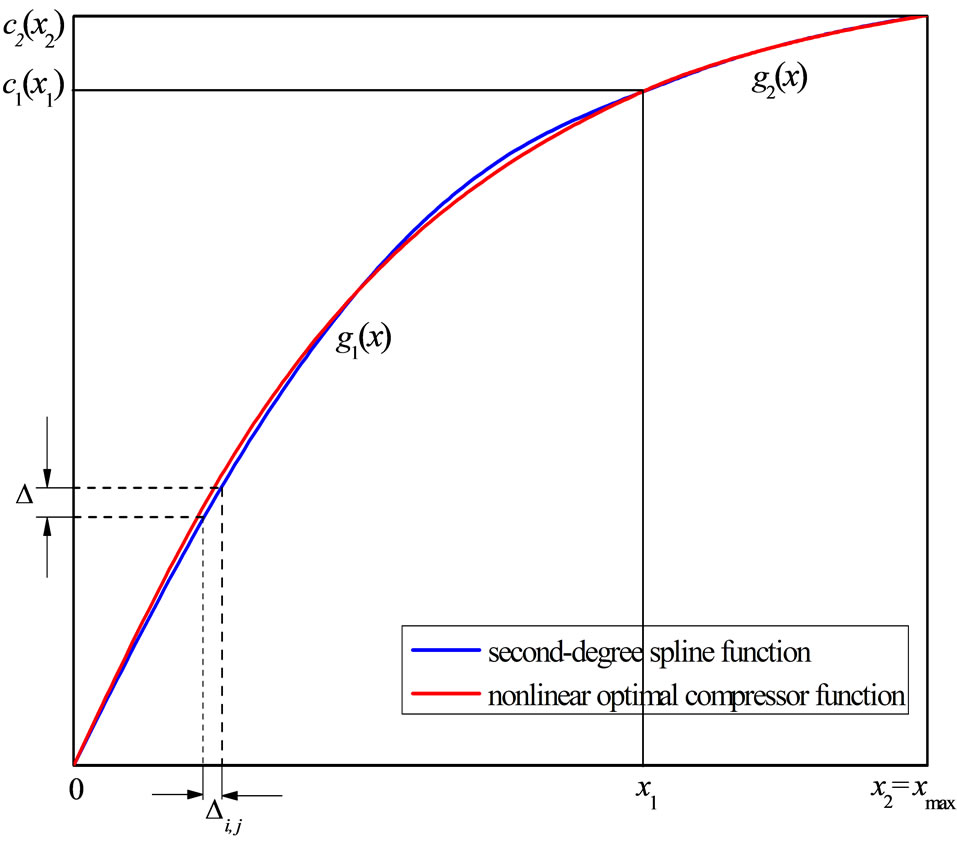
Figure 1. Second-degree spline function and nonlinear optimal compressor function for the number of segments 2L = 4.
where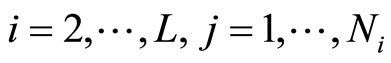 . For the yi,j is taken the solution that belongs to the spline function domain. Observe that indexes i and j indicate on the j-th reproduction levels within the i-th segment. Cells lengths per segments of the considered quantizer is equal to:
. For the yi,j is taken the solution that belongs to the spline function domain. Observe that indexes i and j indicate on the j-th reproduction levels within the i-th segment. Cells lengths per segments of the considered quantizer is equal to:
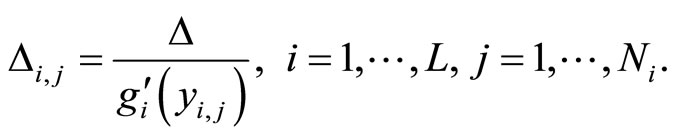 (15)
(15)
Denoted by 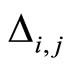 the j-th cells lengths within the i-th segment.
the j-th cells lengths within the i-th segment.
The granular distortion is determined by Bennett’s integral [1-3]:
 (16)
(16)
The granular distortion for the proposed model, based on formula (16), is equal to:
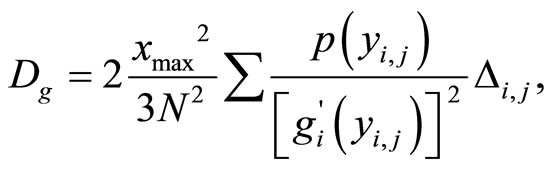 (17)
(17)
where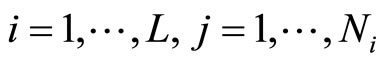 .
.
4. Optimization of Quantizer’s Segment Threshold
In this Section, the segment threshold optimization is described. Solving the system of equations defined by Equation (3), where is the optimal value of the support region, xL = xmax, defined by Equation (10), the expressions for determining coefficents ri, pi, qi, i = 1, ···, L are obtained. The values of coefficents ri, pi, qi, i = 1, ···, L depend on the value of the segment threshold xi. The segment threshold xi is determined in the following:
Step 1. Based on the coefficents ri, pi, qi, i = 1, ···, L expressed depending on the segment threshold xi, the second-degree spline functions, gi(x), defined by Equation (1) is desgined.
Step 2. On the basis of the second-degree spline functions obtained in this way, gi(x), the proposed quantizer as described in Section 3 is designed. This way, an expression for SQNR of proposed quantizer depending on the segment threshold xi is achieved.
Step 3. The segment threshold xi is numerically determined so that maximal SQNR value of proposed quantizer is achieved (see Figures 2 and 3).
5. Numerical Results and Conclusions
Numerical results presented in this section are obtained for the case when the number of segments is equal to 2L = 4 and for number of levels N = 16 and N = 32. For the number of segments 2L = 4, the approximate quadratic spline function g(x) defined by Equation (1) is equal to:
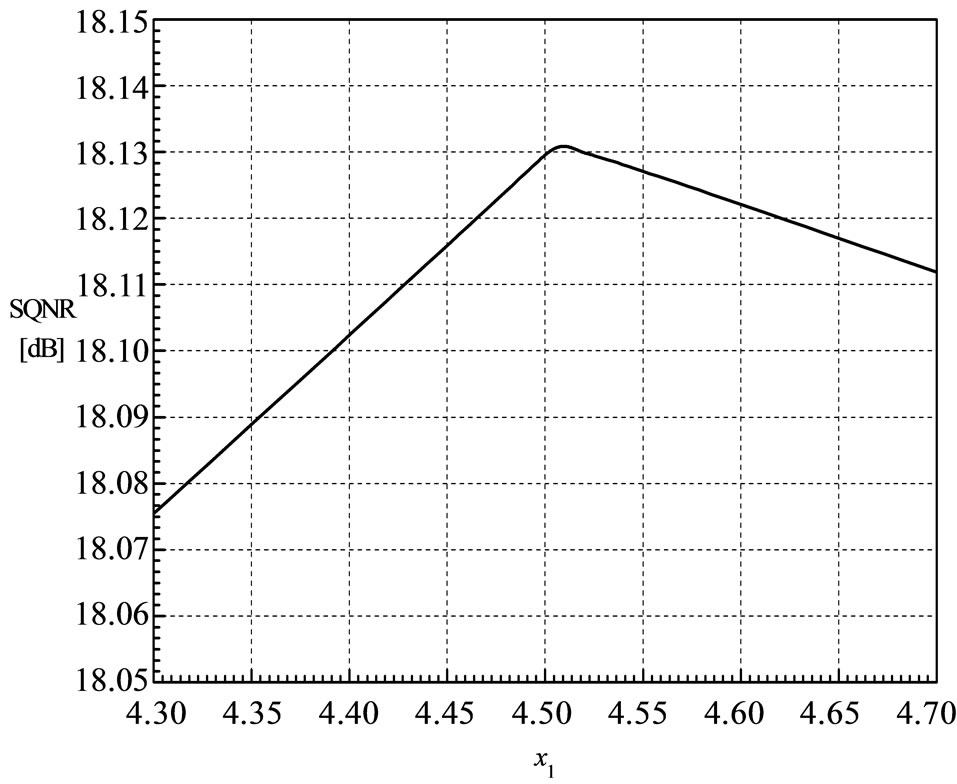
Figure 2. Numerical determination of the segment threshold x1 for the number of levels N = 16.
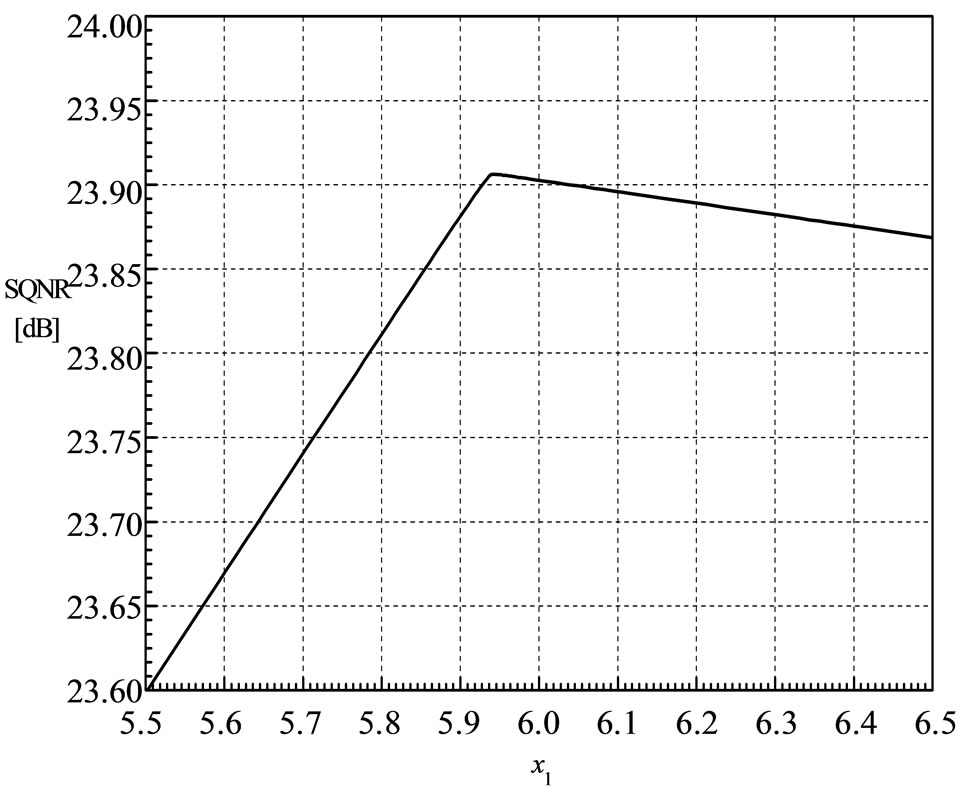
Figure 3. Numerical determination of the segment threshold x1 for the number of levels N = 32.
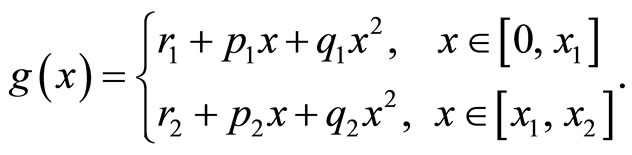 (18)
(18)
The number of conditions set is equal to the number of coefficients that should be determined. In fact, as we have three knotes and two subintervals (see Figure 1), and each second-degree polynomial has three coefficients, means to determinate the six coefficients in total [11]. Solving the system of equations defined by Equation (3), the coefficents r1, p1, q1, r2, p2, q2 are determined. The values of coefficents r1, p1, q1, r2, p2, q2 depend on the value of the segment threshold x1 which is numerically determined as described in Section 4.
In Figures 2 and 3 the dependence of SQNR of the proposed quantizer model on the segment threshold x1 for the number of levels N = 16 and N = 32 is shown. Based on Figure 2 it can be concluded that the maximal value of SQNR of the proposed quantizer is achieved for the value of the segment threshold x1 = 4.51. Also, based on Figure 3 it can be concluded that the maximal value of SQNR of the proposed quantizer is achieved for the value of the segment threshold x1 = 5.94.
Table 1 shows the values of SQNR of the proposed quantizer which segment threshold x1 numerically determined, (SQNRN), the values of SQNR of the proposed quantizer having equidistant segment thresholds (the segment threshold x1 is at the middle of support region) [7], (SQNRS), and the values of SQNR of nonlinear optimal companding quantizer, c(x):
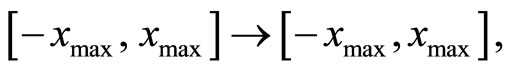
(SQNRO), for the number of levels N = 16 and N = 32. The granular distortion Dg and the overload distortion Do of nonlinear optimal companding quantizer defined as in [1-3]:
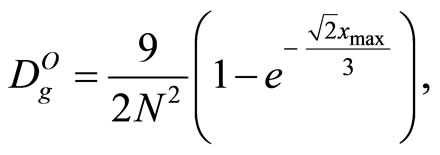 (19)
(19)
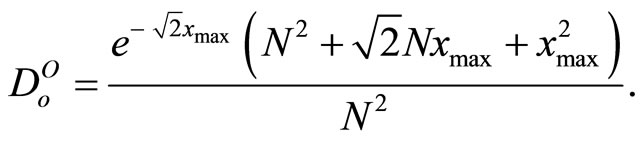 (20)
(20)
In Figure 4 dependency of SQNRN, SQNRS and SQNRO on the number bits per sample (R = 4 bit/sample and R = 5 bit/sample) is shown. Analyzing the results shown in Table 1 and Figure 4, one can notice that design of quantizer based on approximate spline of degree 2, with the optimized segment threshold x1, achieved higher SQNR than design of quantizer based on approximate spline of degree 2 with the segment threshold x1 that is it the middle of the support region. Also, analyzing the results shown in Table 1 and Figure 4, one can conclude that design of quantizer based on approximate spline of degree 2, with the optimized segment threshold x1, achieved SQNR very close to that of nonlinear optimal companding quantizer.
Comparing the performance of the proposed quantizer model with the optimized segment threshold x1, with the quantizer model having equidistant segment thresholds [7], and with the nonlinear optimal companding quantizer [1-3], it can be concluded that the proposed model is a very effective solution because a simple quantizer model achieves a high quality signal. For the case when the number of levels is lower than 16, the complexity of the

Table 1. The values of SQNRN, SQNRS and SQNRO for the number of levels N = 16 and N = 32.
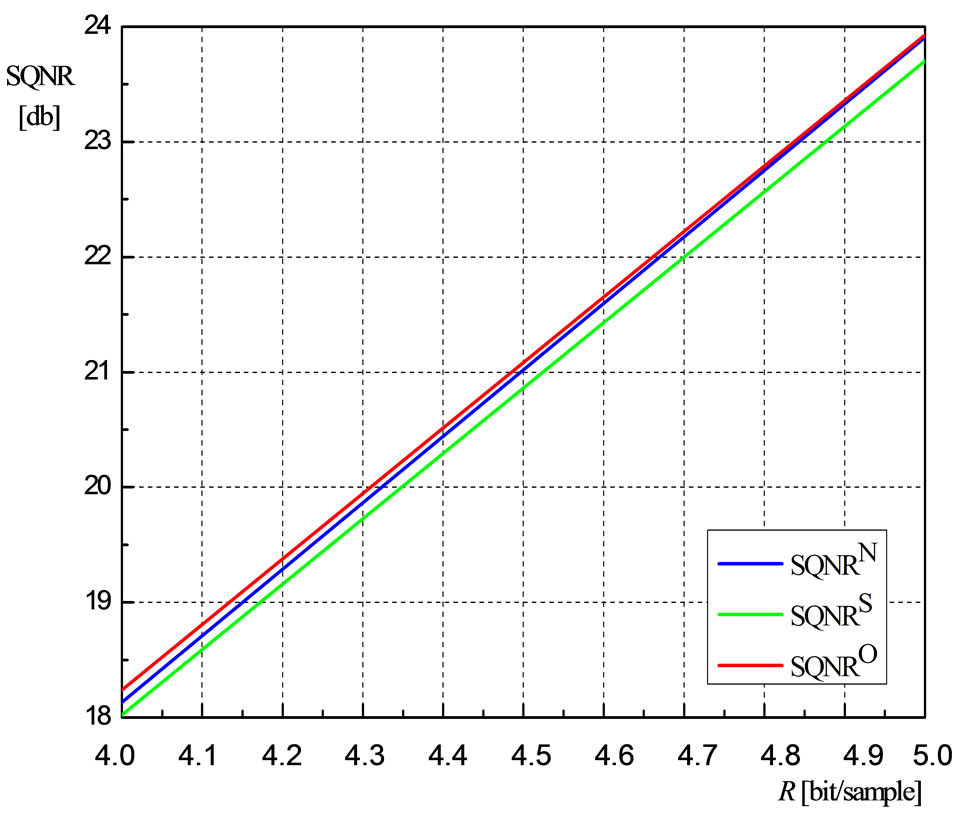
Figure 4. Dependency of SQNRN, SQNRS and SQNRO on the number bits per sample.
proposed quantizer model may be larger than the optimal Lloyd-Max’s scalar quantizer model [1-3]. For the case when the number of levels is more than 32, the complexity of the proposed quantizer model becomes high. Due to these limitations, this paper analyzes the quantizer model for the number of levels N = 16 and N = 32, i.e. for the number bits per sample R = 4 and R = 5. The proposed quantizer model besides Laplacian PDF, is convenient for other probability density functions.
6. Acknowledgements
This work is partially supported by Serbian Ministry of Education and Science through Mathematical Institute of Serbian Academy of Sciences and Arts (Project III44006) and by Serbian Ministry of Education and Science (Project TR32035).
REFERENCES
- N. S. Jayant and P. Noll, “Digital Coding of Waveforms, Principles and Applications to Speech and Video,” Prentice Hall Secondary Education Division, Upper Saddle River, 1984.
- A. Gersho and R. M. Gray, “Vector Quantization and Signal Compression,” Kluwer Academic Publishers, Boston, Dordrecht, London, 1992. doi:10.1007/978-1-4615-3626-0
- L. R. Rabiner and R. W. Schafer, “Introduction to Digital Speech Processing,” Foundations and Trends in Signal Processing, Hanover, 2007.
- J. Nikolić, Z. Perić, D. Antić, A. Jovanović and D. Denić, “Low Complex Forward Adaptive Loss Compression Algorithm and ITS Aplication in Speech Coding,” Journal of Electrical Engineering, Vol. 62, No. 1, 2011, pp. 19-24. doi:10.2478/v10187-011-0003-5
- Z. Perić, M. Petković and M. Dinčić, “Simple Compression Algorithm for Memoryless Laplacian Source Based on the Optimal Companding Technique,” Informatica, Vol. 20, No.1, 2009, pp. 99-114.
- Z. Perić and J. Nikolić, “Analysis of Compressor Function for Laplacian Source’s Scalar Compandor Construction,” Data Recording, Storage and Processing, Vol. 8, No. 2, 2006, pp. 15-24.
- L. Velimirović, Z. Perić, J. Nikolić and M. Stanković, “Design of Compandor Quantizer for Laplacian Source for Medium Bit Rate Using Spline Approximations,” Facta Universitatis, Vol. 25, No. 1, 2012, pp. 90-102.
- S. Na, “On the Support of Fixed-Rate Minimum MeanSquared Error Scalar Quantizers for a Laplacian Source,” IEEE Transactions on Information Theory, Vol. 50, No. 5, 2004, pp. 937-944. doi:10.1109/TIT.2004.826686
- Z. Perić, J. Nikolić and D. Pokrajac, “Estimation of the Support Region for Laplacian Source Scalar Quantizers,” Journal of Electrical Engineering, Vol. 58, No. 1, 2007, pp. 47-51.
- Z. Perić, J. Nikolić and D. Pokrajac, “Analysis of Support Region for Laplacian Source’s Scalar Quantizers,” Proceedings of 7th IEEE Conference on Telecommunications in Modern Satelite, Cable and Broadcasting Services TELSIKS 2005, Niš, 28-30 September 2005, Vol. 2, pp. 491-494.
- W. Cheney and D. Kincaid, “Numerical Mathematics and Computing,” 6th Edition, Thomson Higher Education, Belmont, 2008.
NOTES
*Corresponding author.

